
SELF-ORGANIZING SUPPLY NETWORKS
Autonomous Agent Coordination based on Expectations
Jan Ole Berndt
Center for Computing and Communication Technologies (TZI), Universit¨at Bremen, Am Fallturm 1, 28359 Bremen, Germany
Keywords:
Agent coordination, Self-organization, Expectations, Systems theory, Logistics, Supply networks.
Abstract:
Supply networks are faced with the contradictory requirements of achieving high operational efficiency while
retaining the ability to adapt to a changing environment. Decentralized approaches representing logistics
entities by autonomous artificial agents must therefore be enabled to structure and operate supply networks
efficiently according to the domain’s inherent dynamics caused, for instance, by changing customer demands
and network participants entering or leaving the system. In this paper, a novel approach to self-organization
for multiagent systems is presented, avoiding a priori assumptions of agent characteristics by generating ex-
pectations from observable behavior.
1 INTRODUCTION
Logistics plays a major role in globalized economy.
Industrial production and trade require efficient and
reliable supply networks. Growing interrelations be-
tween these networks and the inherent dynamics of
the logistics domain result in a high complexity of
global supply processes (H
¨
ulsmann et al., 2008). Ap-
plication of conventional centralized planning and
control to these processes suffers from that complex-
ity. Therefore, a need arises for decentralized meth-
ods employing autonomous actors representing logis-
tics entities and objects (H
¨
ulsmann et al., 2006).
From the artificial intelligence point of view, these
autonomous entities can be represented by intelligent
software agents to model logistics networks as mul-
tiagent systems (MAS). These systems may be used
to simulate, evaluate, and actually implement new ap-
proaches in autonomous logistics (Schuldt, 2010).
Coordination and cooperation of autonomous en-
tities is the challenging task that has to be addressed
in order to develop such approaches. In the logis-
tics domain, coordination is faced with the contradic-
tory requirements of achieving high operational effi-
ciency while retaining the system’s ability to adapt to
a changing environment. Supply networks, therefore,
need to achieve high performance rates concerning as-
set utilization, cost reduction, and customer satisfac-
tion on the one hand. On the other hand, they are
required to employ flexible and robust structures in
order to react to unforeseen changes caused by the
domain’s inherent dynamics.
In this paper, a novel approach for self-structuring
multiagent systems is presented. Considering partic-
ular challenges in logistics network configuration and
operation, as elaborated in the next section, agent co-
ordination mechanisms are investigated as a means
for organizing decentralized behavior in logistics net-
works. These considerations form the basis for the de-
velopment and application of expectation-based self-
organization as an adaptive structuring paradigm for
multiagent systems based on social systems theory.
That approach is evaluated in a simulated supply net-
work scenario according to coordination effort and lo-
gistics performance. Finally, the achievements of this
paper are recapitulated in a concluding summary.
2 SELF-ORGANIZING SUPPLY
NETWORKS
In order to solve repeatedly occurring coordination
problems in decentralized systems efficiently, orga-
nizational structures have to be established (Horling
et al., 2004). Yet, it is unclear which kind of struc-
ture is applied best, given a particular coordination
problem. Consider, for instance, a supply network as
partly shown in Figure 1: In this network, the partici-
pants must choose which subset of the depicted pos-
sible relationships between each two tiers (pictured as
arrows in the direction of material flows) actually to
establish. This decision has to take into account cost
considerations as well as the responsiveness and reli-
104
Ole Berndt J..
SELF-ORGANIZING SUPPLY NETWORKS - Autonomous Agent Coordination based on Expectations.
DOI: 10.5220/0003164001040113
In Proceedings of the 3rd International Conference on Agents and Artificial Intelligence (ICAART-2011), pages 104-113
ISBN: 978-989-8425-41-6
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

ability of possible business partners in order to enable
efficient operations within the network.
Tier 1 suppliers OEM Distributors/Retailers Consumers
...
...
...
Figure 1: Schematic diagram of a supply network showing
all possible relationships between the participants.
Thus, a supply network can be represented as a
graph consisting of logistics entities as its nodes and
their possible business relationships as edges. Estab-
lishing an organizational structure refers to the choice
of a subgraph restricting the set of edges to a subset of
all possible ones. An efficient organizational structure
then minimizes the actually instantiated relationships
while maximizing the achieved operations outcome
according to logistics performance measures.
However, due to the dynamics of logistics pro-
cesses, conventional design time evaluation and opti-
mization of these organizational structures is not suffi-
cient in terms of flexibility and robustness. Increasing
demands of the final consumers, for example, require
structural modifications in the distribution part of the
supply network in order to fulfill those demands: Ad-
ditional storage capacity has to be allocated and even
completely new channels of product distribution must
be established. Thus, the structures in that part the
supply network need to be refined, i.e., further or
other options of business relationships must be instan-
tiated.
This is but an example for the dynamics in lo-
gistics that is further aggravated by the openness of
those systems (Brauer et al., 2002): Not only con-
sumer demand changes as well as unforeseen fail-
ures of scheduled operations may happen (leading to
the need of dynamic replanning and reallocation of
resources), but the logistics market itself may alter.
New competitors as well as new customers may en-
ter, causing further changes in demand, prices, and
requirements of products and services. These devel-
opments evoke the need for each participant to con-
stantly adapt his relationships to customers and sup-
pliers in order to secure market shares and to fulfill the
customers’ needs. Such an adaption, furthermore, af-
fects other business relationships within the network,
requiring an extended refinement of supply partner-
ships therein.
Thus, modeling and operating supply networks
with multiagent systems requires the agents’ ability
to establish organizational configurations that allow
for efficient operation, while being flexible enough
(i.e., alterable) to cope with the dynamics of logistics
processes. Hence, the need arises for self-organizing
MAS that autonomously arrange their structure in ac-
cordance with dynamically changing conditions. In
this context, self-organization is therefore considered
as the emergent evolvement and modification of or-
ganizational structures defining business relationships
between supply network partners.
3 AGENT COORDINATION
In order to be able to autonomously coordinate their
activities (e.g., to establish and operate logistics net-
works), artificial agents need to interact with each
other. For this purpose, agent communication lan-
guages that are based on speech acts between agents
are commonly used (Finin et al., 1994; Foundation
for Intelligent Physical Agents [FIPA], 2002a). On
the basis of these speech acts, a range of interaction
and negotiation protocols haven been developed that
may be used to coordinate agent behavior. Patterns of
interaction then reflect relationships between the par-
ticipants and, thus, express the structure of the mul-
tiagent system. In the opposite sense, structuring a
supply network modeled as a MAS means to define
channels and modes of agent communication.
Consequently, a wide variety of different struc-
turing paradigms for MAS has been proposed (cf.
Horling and Lesser (2005) for a comprehensive
overview). These structures range from strict hierar-
chies to market-based methods. While the former use
centralized decision-making at the top and distributed
processing of concrete tasks at the bottom, the latter
are completely decentralized and rely on negotiations
for each single task rather than on any middle or long
termed relationships. In order to make use of such
predefined mechanisms, the expected dynamics of the
application domain must be estimated, as they differ
in their ability to handle changing conditions as well
as in their required effort for coordinating the actions
of a network’s members (Schillo and Spresny, 2005).
However, choosing a prototypical organizational
approach for a whole network may not be suffi-
cient. In fact, heterogenous relationships may be re-
quired between agents in different parts of the sup-
ply network. Moreover, predetermining agent inter-
action patterns will neccessarily lead to a compro-
mise between efficient operation and adaptive behav-
SELF-ORGANIZING SUPPLY NETWORKS - Autonomous Agent Coordination based on Expectations
105

ior: While, for example, negotiation based interac-
tion paradigms are highly adaptive when it comes to
changing behavior of participating agents (as they al-
low for determining the best result given any condi-
tions), they lead to a large overhead of communica-
tion and computation effort as every interaction task
involves all possible participants among the agents.
In order to overcome that problem, methods have
been proposed for subdividing MAS into teams of
agents with similar properties and objectives. The
model for cooperation (Wooldridge and Jennings,
1999) provides a formal description of such team
building among any number of autonomous agents
for distributed problem solving. It includes determi-
nation of potentials for cooperative acts, formation of
teams, distributed planning, and the actual process-
ing of plans. In the logistics domain, team formation
methods have shown benefits in terms of increased re-
source utilization efficiency while reducing the com-
munication effort of agents performing similar tasks
(Schuldt, 2010).
Yet, clustering agents in teams usually focuses
on short termed behavior and tasks, rather than on
middle and long term structures in agent interaction.
Furthermore, team formation processes rely on the
exchange of information about agent properties and
goals. Hence, they assume any participating agents
to behave benevolently, i.e., to be trustworthy. In an
open system, however, agents may be confronted with
deceitful behaving participants (Nickles et al., 2005)
or others simply not willing to share such information.
Thus, potential interaction partners in open MAS
cannot be assumed a priori to exhibit particular be-
havioral characteristics. In fact, they appear as black
boxes and, therefore, must be observed by the other
agents or the system designer in order to determine
their characteristics during runtime of the system.
Based on such observations, a structuring approach
for MAS has been proposed, using explicit model-
ing of expectations concerning communication flows
(Brauer et al., 2002; Nickles and Weiß, 2005). This
approach which is inspired by the sociological theory
of communication systems (Luhmann, 1995) estab-
lishes a notion of communicative agent behavior that
is reflected by the modeled expectations.
Feeding those expectations back into the decision-
making process of interacting agents offers a promis-
ing foundation for self-structuring MAS, as they re-
flect other agents’ characteristics inferred from their
observable behavior. Customer demands, for in-
stance, can be observed from the incoming orders on
the supplier’s side. The supplier can establish ex-
pectations regarding the customers’ behavior and then
adapt his own behavior based on these expectations.
Hence, the system as a whole is enabled to adapt to
implicit characteristics and external impacts by the
agents refining their communication patterns in terms
of business relationships accordingly, i.e., the system
organizes itself.
To summarize, agent coordination refers to com-
munication processes between these agents. Proto-
typical coordination mechanisms lead to a compro-
mise between operational efficiency and flexibility
with regard to dynamic environments while dynamic
team formation requires additional behavioral as-
sumptions to overcome these problems. The systems-
theoretical perspective of expectations structuring
agent interaction (rather than assumptions and com-
mitments), however, provides a promising foundation
for self-organization as a paradigm for multiagent co-
ordination.
Nevertheless, in the approach by Brauer et al.
(2002), expectations reflecting and guiding agent be-
havior are modeled by the system designer as an ex-
ternal observer. Yet, self-organization requires orga-
nizational structures to emerge from the system’s op-
erations without external intervention; i.e., the men-
tioned feedback loop has to be closed within the mul-
tiagent system. Thus, in the next section, the no-
tion of double contingency is introduced, describ-
ing the emergence of mutual expectations structuring
communication systems between agents appearing as
black boxes. In the following, this concept is oper-
ationalized in order to demonstrate its ability to en-
able autonomous coordination of agent communica-
tion systems.
4 EXPECTATION-BASED
SELF-ORGANIZATION
According to the sociologist Niklas Luhmann, double
contingency denotes both the fundamental problem of
social systems constitution as well as its own solution
leading to the emergence of such systems (Luhmann,
1995, pp. 103–136). Referring to Parsons and Shils
(1951), he points out that, given two black boxes al-
ter and ego, ”if alter makes his action dependent on
how ego acts, and ego wants to connect his action to
alter’s“ (Luhmann, 1995, p. 103), they reciprocally
block their ability to act at all.
The solution to that problem, however, lies in the
interdependency of actions, as well. As soon as alter
or ego behave in whatever way, action becomes not
only possible, but social structures emerge from the
self-referential circle of mutually dependent actions.
In fact, those structures consist of expectations evolv-
ing from, e.g., ego’s observation of his own as well as
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
106

alter’s actions that, in turn, guide the selection of ego’s
subsequent actions. Hence, a feedback loop of obser-
vation, expectation, selection, and operation (action)
emerges.
In the context of multiagent systems, double con-
tingency may be viewed analogically as the problem
of determining interaction opportunities. It also de-
notes its own solution through the emergence of ex-
pectations guiding agent communication as the fun-
damental operation in MAS. As a starting point, the
simulation model by Dittrich et al. (2003) can be
used: They simulate and analyze Luhmann’s concept
of double contingency in a scenario of two agents
interacting with each other by exchanging messages
with varying content. The agents memorize a certain
number of these messages and select their response
according to expectations calculated from the entries
in their memories. The approach by Dittrich et al.
shows the evolvement of stable interaction patterns
from the agents’ behavior under a wide range of pa-
rameter conditions (Dittrich et al., 2003, sec. 3 and
5).
In an extension of their own model, Dittrich et al.
furthermore examine the emergence of social order
among an arbitrary number of agents (Dittrich et al.,
2003, sec. 6). To this end, they introduce a random
choice of two agents in each simulation step, letting
them interact in the same way as in the basic dyadic
setting. Their results show that, for growing num-
bers of agents, stable interaction patterns only evolve
if alter’s behavior reflects the average agent behavior
within the system and if the agents are able to observe
more pairwise encounters than they are involved in
themselves Dittrich et al. (2003).
Those requirements as well as their abstract model
of message contents, however, prevent an application
of that approach for self-organization in MAS follow-
ing particular puposes. Choosing agent pairs for inter-
action at random contradicts the objective of emerg-
ing agent relationships. In fact, self-organization as
defined above refers to the choice of interaction part-
ners among the set of all agents in a MAS in its very
core. Thus, that selection must be based on expecta-
tions regarding interaction outcomes, as well. More-
over, in applied self-organizing MAS (e.g., for model-
ing supply networks), the semantics of message con-
tents depending on the respective application domain
is a crucial factor for the determination of such out-
comes. Hence, it has to be considered when generat-
ing agent expectations.
Therefore, in the following, a model of double
contingency is developed, based on the basic ap-
proach by Dittrich et al. (2003), allowing for the ap-
plication of self-organizing coordination of an arbi-
trary number of agents. Moreover, the original model
using meaningless messages is enriched with seman-
tics derived from the logistics domain, being compat-
ible with a standard interaction protocol.
4.1 Modeling Double Contingency
In this model, agent operations consist of sending
FIPA-ACL compliant messages (Foundation for In-
telligent Physical Agents [FIPA], 2002a). Observing
them refers to their storage in an agent’s memory,
which is used to calculate selection values for all pos-
sible replies. The next message to be sent by the ob-
serving agent is then selected according to these val-
ues. Thus, an agent’s communicative behavior exclu-
sively depends on its memorized observations of other
agents’ behavior, avoiding any further assumptions of
their internal properties and characteristics. The basic
steps enabling the agents to self-organize hence are:
1. The observation of incoming messages sent by
other agents
2. The selection of messages to be sent to other
agents
The memory of an agent is modeled as a vec-
tor MEM = (mem
1
, . . . , mem
n
) with a fixed length n,
where each entry mem
i
denotes a tuple of messages
m ∈ M (M being the set of all possible messages),
the second one being the response to the first one:
mem
i
= hm
received,i
, m
sent,i
i. An agent possesses two
of those memories, MEM
ego
and MEM
alter
, storing
its own reactions to perceived messages and observed
others’ reactions to its own messages, respectively.
Thus, observation takes place when sending a mes-
sage m
sent
by adding it to MEM
ego
together with the
last received message m
received
as well as when receiv-
ing a message m
received
by adding it to MEM
alter
to-
gether with the last message m
sent
the agent sent itself.
Each time, a tuple of messages is memorized, if this
would lead to a memory size > n the oldest entry is
removed from the memory.
This way to model an agent’s memory is an im-
portant modification of that by Dittrich et al. (2003),
differing in alter not only being considered one single
agent, but the whole community of agents other than
ego. This reflects Luhmann’s understanding of dou-
ble contingency as a phenomenon not restricted to an
encounter of two individuals, but occurring between
systems in a generalized manner (Luhmann, 1995,
pp. 105–106). Thus, expectations may well be es-
tablished regarding the behavior of the whole MAS,
considering it as a social system. The entries in its
memory therefore reflect an agent’s observations of
its interaction with all of its fellow agents.
SELF-ORGANIZING SUPPLY NETWORKS - Autonomous Agent Coordination based on Expectations
107

Moreover, this interpretation of double contin-
gency between an agent and the whole agent commu-
nity allows not only for the content of a message to
be selected according to memorized experience from
former agent interactions, but also for using the se-
lection mechanism to determine its receivers (i.e., the
interaction partners). Hence, the advantages of the
dyadic model by Dittrich et al. (2003) regarding struc-
tural emergence can be retained while avoiding the
drawbacks of its extension for an arbitrary number of
agents.
In order to calculate expectations from the agents’
memories, a function lookup : MEM × M × M −→
[0, 1] is defined, that estimates the probability of one
message being observed as the response to another:
lookup(MEM, m
received
, m
sent
) =
l
m
received
,m
sent
P
m
j
∈M
l
m
received
,m
j
(1)
where
l
m
received
,m
sent
=
c
M
|M|
+
n
X
i=1
n + 1 − i
n
·
1 if mem
i
ˆ=hm
received
, m
sent
i
0 else
(2)
Here, mem
i
ˆ=hm
received
, m
sent
i denotes the pairwise
equality of the received and sent messages compared
to those in memory entry mem
i
according to their per-
formatives, sets of receivers and contents. This is the
second major modification of the original model, al-
lowing for considering advanced message semantics
(in contrast to the very abstract message representa-
tion by Dittrich et al. (2003)). Especially the content
of messages depends on the application domain, en-
abling the usage of domain dependent equality mea-
sures (e.g., the distinction of orders for different prod-
uct types). The constant c
M
is used to avoid message
combinations to be regarded completely impossible in
case of missing observations (cf. Dittrich et al. (2003,
sec. 9.4)). With mem
1
being the most recent observa-
tion, this function uses a linear discount model to re-
flect the agent gradually forgetting past observations.
Two kinds of expectations are then calculated for
selecting an agent’s next message: An expectation
certainty (EC) that denotes an agent’s certainty about
which reaction to expect from the MAS following its
own message and an anticipated expectation (AE)
1
that reflects an agent’s anticipation of other agents’
expectations towards its own behavior.
1
Dittrich et al. (2003) call this expectation-expectation
(EE), literally translating Luhmann’s original German term.
Luhmann, however, uses anticipated expectation in the En-
glish edition of his main work (Luhmann, 1995).
The EC is calculated using a function certainty :
MEM × M −→ [0, 1] that is based on a modified ver-
sion of the standard deviation in order to estimate an
agent’s assuredness over the possible reactions on its
next message m
sent
(Dittrich et al., 2003, sec. 2.1 and
9.5):
EC
m
sent
= certainty(MEM
alter
, m
sent
) (3)
with
certainty(MEM, m
sent
) =
v
u
t
|M|
|M| − 1
X
m
j
∈M
1
|M|
− lookup(MEM, m
sent
, m
j
)
!
2
(4)
This linear function returns a value of 0 for uniformly
distributed probability estimations over the others’
possible reactions to an agent’s message and a value
of 1 for the most inhomogenous distribution of those
estimated probabilities. Thus, it reflects the certainty
of the agent expecting a particular response to its mes-
sage. Note, however, that the lookup of each value for
the possible reactions of the MAS is used with the
sent message as its first argument. This is because
MEM
alter
contains ego’s observations of himself from
alter’s perspective. Thus, as ego’s m
sent
is what alter
receives from him, it is treated as the received mes-
sage in MEM
alter
.
On the other hand, the AE is calculated directly
through the lookup-function as the estimated proba-
bility of the agent’s next message m
sent
in response
to the last received message m
received
(Dittrich et al.,
2003, sec. 2.1):
AE
m
sent
= lookup(MEM
ego
, m
received
, m
sent
) (5)
As MEM
ego
stores all observations of ego’s responses
to received messages, Equation 5 reflects ego’s antici-
pation of alter’s perception of his behavior. Hence, the
AE denotes an agent’s estimation of what is expected
from itself by the community of its fellow agents.
Both types of expectations are finally combined in
a weighted sum to a selection value V for each op-
tion for a next message m
sent
∈ M. This value rep-
resents the potential of a given message to stabilize
the system, as high selection values reproduce them-
selves when a corresponding message is chosen and
thus fed back into the control loop. Differing from
Luhmann’s theory and the model by Dittrich et al.,
at this stage, an explicitly represented utility function
utility : M −→
+
is further introduced. This function
enables V not only to reflect the system’s stability, but
also directs the agent’s behavior towards domain de-
pendent performance criteria. Thus, V
m
sent
is given by
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
108

the following equation:
V
m
sent
=(αEC
m
sent
+ (1 − α)AE
m
sent
)
· utility(m
sent
) +
c
f
|M|
(6)
Here, the parameter α ∈ [0, 1] weights the balance be-
tween EC and AE, while c
f
is another constant to
avoid marginal differences in the weighted sum to
cause overly high effects on the selection of messages
and to retain an agent’s ability to try out alternative
messages, i.e., to occasionally explore the possibility
space (cf. Dittrich et al. (2003, sec. 9.1)).
Calculating V
m
sent
for all possible message options
m
sent
∈ M enables an agent to select its operations
(i.e., the messages to be sent) according to the expec-
tations calculated from observations of its interaction
with other agents within a MAS. As the selection of
an operation leads to further observations, the afore-
mentioned feedback loop is closed. Yet, the method
of actually choosing an operation in accordance with
the calculated selection values remains to be deter-
mined. That method depends on an agent’s role in the
MAS and is introduced in the next subsection.
4.2 Representing the Logistics Domain
When modeling supply network participants as au-
tonomous agents, these agents may have different ca-
pabilities. As shown in Figure 2, they can be classified
in primary producers that produce raw materials with-
out consuming anything, final consumers that only
consume products, and manufacturers that consume
materials and semi-finished parts in order to transform
them into new parts and products. Concerning the
business relationships between the entities, it is suf-
ficient to distinguish the agents by their roles as pro-
ducers and/or consumers of certain goods (manufac-
turers acting both as producers and consumers). Their
respective possible relationships as suppliers and cus-
tomers are depicted by the edges between the entities
in Figure 2 (with the left hand side of an edge being
attached to a supplier and its right hand side being
connected to the respective customer).
These relationships denote possible occurrences
of order/delivery processes, that form the fundamen-
tal operations of a logistics system. They are mod-
eled using the FIPA-REQUEST interaction protocol
(Foundation for Intelligent Physical Agents [FIPA],
2002b): An order is placed by sending a REQUEST
message containing a product type and the requested
amount of that good to any subset of the possible sup-
pliers for this product. An answer with the REFUSE
or FAILURE performative is considered a failure to
deliver while an INFORM leads to the supplier agent
removing the specified amount of products from its
inventory and the customer adding it to its own one.
A2
A2
A2
B2A2
B2A2
B2A2
B2
B2
B2
Primary production Manufacturing Final consumption
Figure 2: A simple supply network depicting agent roles
and relationships in the logistics domain.
For selecting their messages based on their expec-
tations, the agents have different objectives, according
to their respective roles. These are represented in:
1. An agent’s utility function;
2. The selection method used by an agent.
From a customer’s point of view, there are two ob-
jectives: On the one hand, a customer strives to max-
imize the number of fulfilled orders to enable con-
tinuous product consumption. On the other hand, this
role is also responsible for the amount of messages to
be handled in the MAS depending on the number of
receivers per message. In order to ensure a low com-
munication effort, the second objective is to minimize
the number of order receivers. Thus, when calculating
the selection values for each message, the following
utility function is employed:
utility(m
sent
) =
1
|rec(m
sent
)|
· eor(m
sent
) (7)
Here, rec(m
sent
) denotes the set of receivers of mes-
sage m
sent
and eor(m
sent
) is the estimated order ful-
fillment rate, calculated by:
eor(m
sent
) =
X
m
j
∈M
lookup(MEM
alter
, m
sent
, m
j
)
·
1 if perf (m
j
) = INFORM
0 else
(8)
As perf (m
j
) indicates the performative of message
m
j
, the eor represents the estimated probability of a
positive answer to the given order. Hence, this utility
function favors those orders that have a small number
of receivers while having a high estimated probability
to be fulfilled.
A message m
sent
finally is randomly chosen out
of the set of all possible messages with a probabil-
ity based on its selection value. In order to be able to
SELF-ORGANIZING SUPPLY NETWORKS - Autonomous Agent Coordination based on Expectations
109

adjust the level of randomness in this selection, the se-
lection value is further modified by an exponent γ, al-
lowing for choosing from a range between completely
random selection (γ = 0) and deterministically select-
ing the maximum value (γ = ∞). Therefore, following
Dittrich et al. (2003, sec. 2.1) again, selection is done
using a probability distribution over all possible mes-
sages m
sent
, calculated as follows:
p(m
sent
) =
V
γ
m
sent
P
m
j
∈M
V
γ
m
j
(9)
From a supplier’s point of view, on the other hand,
the objectives are easier to represent. A supplier is
assumed to be generally interested in fulfilling an or-
der if possible. If it is not possible to fulfill all or-
ders, a supplier prefers to maximize the system’s sta-
bility in terms of predictability of further incoming
orders and anticipated expectations of the customers.
In other words, a supplier favors orders by his regu-
lar customers as he can expect them to place further
orders in the future and he can anticipate the expec-
tation of their orders being fulfilled. This setting is
directly represented in the weighted sum of EC and
AE. Thus, the supplier’s utility function remains un-
used (utility(m
sent
) = 1).
For the choice of a message, the selection value
V
m
sent
is calculated for each answer m
sent
∈ M with
perf (m
sent
) = INFORM. The answers are then sorted
by their respective selection values. Beginning with
the highest value, the messages are processed in de-
scending order. As long as the supplier’s inventory
stock level allows for fulfilling the processed order,
an INFORM message is sent. If that is no longer pos-
sible, all subsequent orders are refused.
5 EMPIRICAL EVALUATION
In order to validate the ability of expectation-based
self-organization to efficiently structure and operate
multiagent systems modeling supply networks, that
approach will be compared to the performance of
a system with a previously defined communication
structure. For this purpose, the approach is im-
plemented and applied to an example scenario us-
ing the multiagent-based simulation system PlaSMA
(Schuldt et al., 2008).
5.1 Experimental Setup
In this evaluation, a network with three tiers and three
parallel operating entities is modeled as depicted in
Figure 2. In this sample scenario, each agent pro-
duces and/or consumes an amount of two units of the
product types A and/or B (two A being transformed
into two B by the agents at the manufacturing tier).
Furthermore, every agent has an outbound inventory
capacity of four units per product type, restricting the
amount of goods that can be produced and stored by a
single logistics entity. The agents acting as customers
pursue a policy of ordering an amount of four units
if the respective inventory stock level reaches six or
less.
In the simulation, a message sent by an agent can
be received and processed in the next time slice at the
earliest. Therefore, sending an order and receiving
the response takes two simulation cycles. In that time,
four units of the required type of products can be con-
sumed. Thus, the amount of goods ordered enables
maximal utilization of production and consumption
processes while requiring minimal outbound storage
capacity on the suppliers’ side. However, the thresh-
old of six units for placing an order enables the agents
at the manufacturing tier to build up safety stocks,
allowing for continued production in case of supply
shortfalls and thus compensating disturbances at the
early network tiers.
Prestructuring this network can easily be done by
choosing an arbitrary bijection out of the possible re-
lationships between each two tiers. For each order
following the mentioned policy, this ensures the num-
ber of receivers being one (the possible minimum)
and the supplier to be able to fulfill that order as
soon as enough raw material has been produced in
an initialization phase (as the amount of consumed
goods equals that of produced ones). Thus, such an
arrangement of relationships necessarily leads to a
maximized operation efficiency of the modeled sup-
ply network using a minimal number of sent mes-
sages. Regarding these objectives, it therefore guar-
antees optimal results making it especially suitable as
a reference for the self-organizing approach.
Yet, without prior knowledge of other agents’ ca-
pabilities and relationships, the choice of interac-
tion partners leading to an efficient and reliable net-
work structure is not an obvious one. As the possi-
ble configurations of message receivers for each or-
der correspond to the power set of the set of avail-
able suppliers (without the empty set), in a network
with n tiers and m parallel actors at each tier, the
total number of potential relationships is (m · (2
m
−
1))
n−1
(the possible communication paths through the
network).
2
Thus, in the chosen scenario the self-
2
There are m agents at a tier with 2
m
− 1 possible inter-
action partners, each. The potential paths throw the network
are given by the combination of those options over all n − 1
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
110
organizing agents can choose between 441 possible
interaction patterns leading to different performance
rates. Therefore, in this simple scenario, agent coordi-
nation is already complex enough to make it suitable
for evaluating the efficiency of emerging communica-
tion structures.
For this purpose, the expectation-based agents are
configured as follows: The set of possible orders to be
sent by a customer is given by the possible combina-
tions of their receivers, their performatives, and their
content. As there is only one type and a fixed amount
of units to order per customer, there is only one pos-
sible content. The same holds for the performative, as
an order is always a REQUEST message. Thus, the
set of possible orders is determined by the possible
combinations of a message’s receivers (the power set
of the set of receivers). For the replies, on the other
hand, the receiver as well as their contents are preas-
signed by the incoming orders. Hence, a supplier’s
only choice is between the message performatives ac-
cording to the FIPA-REQUEST interaction protocol.
For generating the results presented in the follow-
ing subsection, the constant values are based on those
used by Dittrich et al. (2003): c
M
= 2 and c
f
= 0.02.
The agent memory size is set to n = 25 for both
MEM
ego
and MEM
alter
, the balance between EC and
AE to α = 0.5, and the customers’ selection value gain
to γ = 3. All agent memories are initially populated
with randomly chosen messages.
In order to validate the approach to expectation-
based self-organization, it is compared to an optimal
configuration as outlined above. The performance is
measured with regard to the final consumers customer
satisfaction rate (i.e., the number of fulfilled orders),
the number of receivers per order, and the utilization
of the final consumers’ product consumption. The
first two criteria directly reflect the customers’ utility
function and give information about the reliability of
emerging relationships between agents (customer sat-
isfaction) as well as about the communication effort
needed to operate the network (message receivers).
Thus, these measures reflect the extend of stability of
the emerging network structures. The consumers’ uti-
lization, on the other hand, is an additional logistics
performance measure that allows to validate the sup-
ply network’s overall operating efficiency in terms of
product throughput rates.
5.2 Results and Discussion
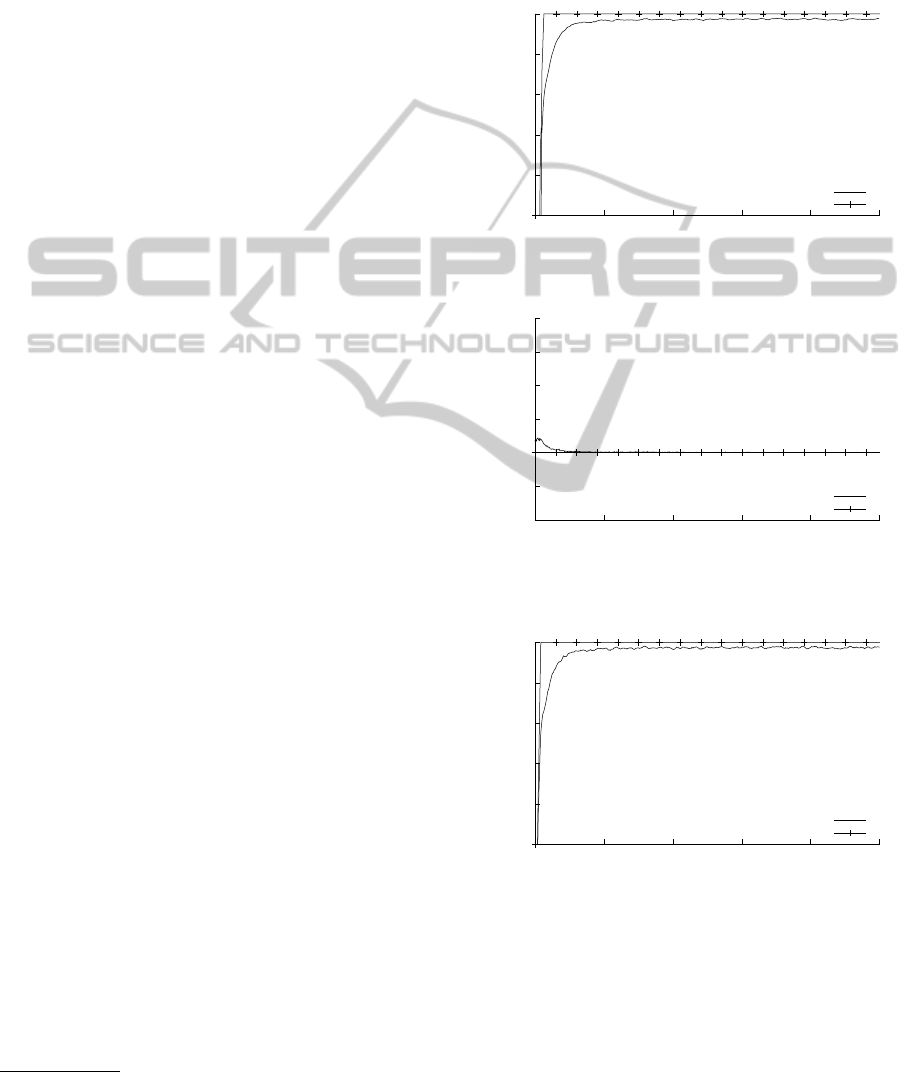
The results depicted in Figures 3–5 show the customer
satisfaction, number of receivers, and consumer uti-
lization as average values over 200 simulation runs.
links between two tiers.
Each run consists of 1000 production and/or con-
sumption operations. For the calculation of the or-
der fulfillment rate, the last ten messages received are
considered for each time slice while the utilization is
measured over the last ten attempts to consume the
respective amount of products.
0
0.2
0.4
0.6
0.8
1
0 200 400 600 800 1000
Customer satisfaction
Simulation time
Self-organizing
Prestructured
Figure 3: Customer satisfaction among the final consumers.
0
0.5
1
1.5
2
2.5
3
0 200 400 600 800 1000
# receivers
Simulation time
Self-organizing
Prestructured
Figure 4: Number of message receivers (orders of final con-
sumers).
0
0.2
0.4
0.6
0.8
1
0 200 400 600 800 1000
Process utilization
Simulation time
Self-organizing
Prestructured
Figure 5: Consumption rate (utilization) among the final
consumers.
For the prestructured reference configuration, the
figures show that there is a short initialization phase
until the inventories of the suppliers are filled high
enough to be able to fulfill the customers’ orders. Af-
ter that phase, the optimal values are reached for the
order fulfillment rate and the customers’ utilization
SELF-ORGANIZING SUPPLY NETWORKS - Autonomous Agent Coordination based on Expectations
111

while the number of receivers per order is always one
by definition.
In the self-organizing network, these levels are
not reached completely. However, the values con-
verge near the optimum, showing that the agents au-
tonomously establish one to one interaction relation-
ships (Figure 4) that still lead to a near optimal order
fulfillment rate of more than 97% (Figure 3). The pro-
cess utilization (Figure 5) as a logistics performance
indicator corresponds to these values, as the agents
always order the minimal amount of products which
directly leads to supply shortfalls in case of refused
orders.
These results reflect the capability of generating
social order as it is observed by Dittrich et al. (2003)
in their original model. Thus, changing their interpre-
tation of a dyadic encounter between individuals to
a more general understanding of double contingency
regarding alter a whole community of entities allows
for transferring the properties of their basic approach
to a multiagent scenario. Therefore, an application of
expectation-based self-organization in MAS based on
Luhmann’s notion of double contingency is possible
without the requirement for a reduction of interaction
to pairwise communication processes or the need for
extended agent observation activities.
Concerning the logistics application, the results
demonstrate that the expectation-based approach to
self-organizing agent interaction is not only capable
of efficiently structuring and operating the modeled
supply network. In fact, it is even able to establish an
optimal configuration of agent communication chan-
nels (one to one relationships) leading to similar per-
formance rates compared to the benchmark arrange-
ment in the course of the simulation. As the agents
occasionally explore alternative interaction options,
delivery failures occur from time to time leading to
slightly less than optimal customer satisfaction and
utilization rates due to the minimal order size and in-
ventory capacities. Regarding these measures, safety
stocks and increased order sizes may compensate that
disturbances to further improve the logistics perfor-
mance.
To summarize, the feedback loop of agent obser-
vation and expectation-based selection of operations
shows the ability to reach near optimal results without
the requirement for a priori assumptions about agent
characteristics (as, e.g., determining the benchmark
configuration requires knowledge of the agents’ pro-
duction and consumption rates) or repetitive negoti-
ations between several agents. As it is not generally
possible to optimally prestructure a logistics network
due to the dynamics of the logistics domain and the
black box nature of agents in open MAS, expectation-
based self-organization provides a promising coordi-
nation method for supply systems being adaptive as
well as operating efficiently.
6 CONCLUSIONS
In this paper, the requirement for adaptive yet efficient
supply networks has been identified. As multiagent
systems provide a means for decentralized model-
ing of logistics networks, possible coordination tech-
niques have been investigated in terms of their appli-
cability to address the identified challenges in supply
network organization. In this context, expectations re-
garding observable behavior have been presented as
a means for dynamically structuring agent relation-
ships, avoiding the need for a priori assumptions re-
garding agent properties and behavior.
Based on theoretical foundations from sociology
(Luhmann, 1995), a simulation approach to emerg-
ing interaction patterns using expectations has been
adapted and generalized to be applicable in multia-
gent systems. That method has been evaluated in a
simulated supply network scenario according to coor-
dination efficiency and reliability as well as logistics
performance.
The simulation results illustrate that self-organ-
ized agent coordination based on mutual expectations
is able to establish organizational structures approx-
imating optimal performance values regarding the
evaluation criteria. Hence, the approach has been
shown to enable efficient interaction of autonomous
entities to emerge solely based on locally observable
agent behavior.
However, there are still questions open for future
examination. While the presented approach performs
very well in a stable agent community with repeat-
ing interaction contents (i.e., a static supply network
setup), it remains to be analyzed in a setting with dy-
namically changing agent memberships and activities.
In such a scenario, a self-organizing network can be
assumed to actually outperform a predefined structure
as the latter is not able to adapt to changing condi-
tions. Furthermore, in that context, an examination
of the different parameters’ impact on the predictabil-
ity and speed of convergence (learning rate) and the
limits of overall performance of the emerging system
structure will give further insights into the capabil-
ities of expectation-based self-organization and may
motivate further refinements of that approach to agent
coordination.
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
112

ACKNOWLEDGEMENTS
This research is partly funded by the German Re-
search Foundation (DFG) within the Collaborative
Research Center 637 “Autonomous Cooperating Lo-
gistic Processes: A Paradigm Shift and its Limita-
tions” (SFB 637) at Universit
¨
at Bremen, Germany.
REFERENCES
Brauer, W., Nickles, M., Rovatsos, M., Weiß, G., and
Lorentzen, K. F. (2002). Expectation-Oriented Analysis
and Design. In Wooldridge, M. J., Weiß, G., and Ciancar-
ini, P., editors, AOSE 2001, LNCS 2222, pages 226–244,
Berlin, Heidelberg. Springer.
Dittrich, P., Kron, T., and Banzhaf, W. (2003). On the Scal-
ability of Social Order: Modeling the Problem of Double
and Multi Contingency Following Luhmann . Journal of
Artificial Societies and Social Simulation, 6(1).
Finin, T., Fritzson, R., McKay, D., and McEntire, R. (1994).
KQML as an agent communication language. In Adam,
N. R., Bhargava, B. K., and Yesha, Y., editors, CIKM
1994, pages 456–463, New York. ACM.
Fischer, K., Florian, M., and Malsch, T., editors (2005). So-
cionics. Scalability of Complex Social Systems. Number
3413 in Lecture Notes in Artificial Intelligence (LNAI).
Springer, Berlin, Heidelberg.
Foundation for Intelligent Physical Agents [FIPA] (2002a).
FIPA Agent Communication Language Specifications.
Standard, FIPA.
Foundation for Intelligent Physical Agents [FIPA] (2002b).
FIPA Request Interaction Protocol Specification. Stan-
dard, FIPA. Document No. SC00026H.
Horling, B. and Lesser, V. (2005). A Survey of Multi-Agent
Organizational Paradigms. The Knowledge Engineering
Review, 19(4):281–316.
Horling, B., Mailler, R., and Lesser, V. (2004). A Case
Study of Organizational Effects in a Distributed Sensor
Network. In Sonenberg, L. and Sierra, C., editors, AA-
MAS 2004, pages 1294–1295, New York. IEEE Com-
puter Society.
H
¨
ulsmann, M., Scholz-Reiter, B., Austerschulte, L.,
Wycisk, C., and de Beer, C. (2008). Autonomous Co-
operation – A Way to Cope with Critical Incidents in
International Supply Networks (ISN)? An Analysis of
Complex Adaptive Logistic Systems (CALS) and their
Robustness. 24th EGOS Colloquium. Vrije Universiteit
Amsterdam.
H
¨
ulsmann, M., Scholz-Reiter, B., Freitag, M., Wycisk, C.,
and De Beer, C. (2006). Autonomous Cooperation as
a Method to cope with Complexity and Dynamics? –
A Simulation based Analyses and Measurement Concept
Approach. In Bar-Yam, Y., editor, ICCS 2006, Boston.
Luhmann, N. (1995). Social Systems. Stanford University
Press, Stanford.
Nickles, M., Rovatsos, M., and Weiss, G. (2005).
Expectation-oriented modeling. Engineering Applica-
tions of Artificial Intelligence, 18(8):891–918.
Nickles, M. and Weiß, G. (2005). Multiagent Systems With-
out Agents – Mirror-Holons for the Compilation and En-
actment of Communication Structures. In Fischer et al.
(2005), pages 263–288.
Parsons, T. and Shils, E., editors (1951). Toward a General
Theory of Action. Harvard University Press, Cambridge.
Schillo, M. and Spresny, D. (2005). Organization: The Cen-
tral Concept for Qualitative and Quantitative Scalability.
In Fischer et al. (2005), pages 84–103.
Schuldt, A. (2010). Multiagent Coordination Enabling Au-
tonomous Logistics. Doctoral dissertation, Universit
¨
at
Bremen.
Schuldt, A., Gehrke, J. D., and Werner, S. (2008). De-
signing a Simulation Middleware for FIPA Multiagent
Systems. In Jain, L., Gini, M., Faltings, B. B., Terano,
T., Zhang, C., Cercone, N., and Cao, L., editors, WI-IAT
2008, pages 109–113, Sydney. IEEE Computer Society
Press.
Wooldridge, M. and Jennings, N. R. (1999). The Coop-
erative Problem-solving Process. Journal of Logic and
Computation, 9(4):563–592.
SELF-ORGANIZING SUPPLY NETWORKS - Autonomous Agent Coordination based on Expectations
113
