
TEAM FORMATION FOR AGENT COOPERATION IN LOGISTICS
Protocol Design and Complexity Analysis
Arne Schuldt
Centre for Computing and Communication Technologies (TZI)
University of Bremen, Am Fallturm 1, 28359 Bremen, Germany
Keywords:
Agents, Cooperation, Team formation, Interaction protocol, Protocol design, Complexity analysis.
Abstract:
Supply network management is a challenging task due to the complexity, dynamics, and distribution of lo-
gistics processes. Delegating process control to intelligent software agents that represent logistics objects
and act on their behalf helps approach these challenges. The resulting problem decomposition reduces the
computational complexity. Dynamics can be dealt with locally. An important prerequisite for coordinated
process control is that agents can cooperate with each other. Based on requirements from logistics, this paper
presents an interaction protocol for team formation. A thorough complexity analysis for the proposed method
is conducted because the arising interaction effort is not obvious as it depends on the number of teams formed.
Therewith, agent developers can estimate the interaction effort and thus the applicability of the method in
advance. Finally, an application of the introduced protocol is outlined.
1 INTRODUCTION
Managing complex supply networks with software
systems is a challenging task. In particular, coordi-
nating logistics processes requires dealing with the
following challenges:
complexity caused by the high number of logistics
objects and their parameters,
dynamics caused, for instance, by transient customer
demands and changes in the environment, and
distribution because logistics processes often span
over multiple companies and even continents.
These properties prevent the application of centralis-
tic and monolithic software systems. Generating op-
timal plans centrally consumes a lot of time. Often,
the dynamics therefore renders these plans outdated
already in the moment their generation is finished.
Moreover, the physical distribution prevents relevant
information from being available centrally.
Consequently, the paradigm of autonomous con-
trol in logistics (Windt and Hülsmann, 2007) dele-
gates decision-making to the participating entities. In
contrast to other approaches (Chaib-draa and Müller,
2006), not only companies or departments, but ac-
tually individual logistics objects are considered au-
tonomous. For instance, shipping containers are
themselves responsible for planning and scheduling
their way through the logistics network. The com-
putational complexity is reduced because each entity
only considers its own parameters and those of co-
operating entities (Schuldt, 2010). This increases re-
activity and robustness of process control because ex-
ceptions can be dealt with locally. Autonomous logis-
tics can be implemented with intelligent agents being
representatives for logistics objects.
An important finding is that individual agents can
frequently not satisfy their logistics objectives on
their own (Schuldt and Werner, 2007). As a conse-
quence, they must cooperate with other agents. The
formal model for cooperation of intelligent agents
(Wooldridge and Jennings, 1999) distinguishes four
consecutive steps of the cooperative problem-solving
process (Figure 1). As a prerequisite, agents must
recognise a potential for cooperation because joint ac-
tion is not reasonable without. Having identified this
potential, agents can form a team. Subsequently, they
collaboratively elaborate a plan. Finally, the team ac-
tion step deals with joint execution of this plan.
This paper focuses on the team formation step.
There is a demand for a particular interaction proto-
col for team formation in logistics because interaction
schemes are underspecified in the original model for
cooperation. This paper has two contributions:
1. Protocol design
2. Complexity analysis
398
Schuldt A..
TEAM FORMATION FOR AGENT COOPERATION IN LOGISTICS - Protocol Design and Complexity Analysis.
DOI: 10.5220/0003164703980405
In Proceedings of the 3rd International Conference on Agents and Artificial Intelligence (ICAART-2011), pages 398-405
ISBN: 978-989-8425-41-6
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

Plan FormationTeam FormationRecognition Team Action
Figure 1: The four steps of the model for cooperation (Wooldridge and Jennings, 1999). As a precondition, agents must
recognise a potential for cooperation. Subsequently, agents form both a team and a joint plan before they actually act jointly.
The protocol design is documented in Section 2. Rel-
evant requirements for team formation in autonomous
logistics are derived and contrasted to existing ap-
proaches. Based on this analysis, an interaction
scheme for team formation is introduced. In order
to estimate the applicability of the new protocol, the
approach is thoroughly analysed with respect to its in-
teraction effort in Sections 3 and 4. Section 5 outlines
an application of the introduced protocol.
2 PROTOCOL DESIGN
Team formation is an important prerequisite for coop-
eration of autonomous logistics entities. Section 2.1
motivates the demand for cooperation by identifying
the potential for cooperation. In particular, relevant
requirements for team formation mechanisms in au-
tonomous logistics are derived. Section 2.2 contrasts
these requirements to existing approaches. Finally,
Section 2.3 presents an agent interaction protocol that
satisfies the identified requirements.
2.1 Motivation and Requirements
As a prerequisite for cooperation among intelli-
gent agents, the model for cooperation demands
that a group of agents can jointly achieve a goal
(Wooldridge and Jennings, 1999). Reasons for acting
collaboratively are twofold. On the one hand, an indi-
vidual agent may not be capable of achieving its goal
in isolation. On the other hand, the agent may have a
goal conflict for all of its respective own actions.
In the first case, agents with complementing ca-
pabilities should form teams in order to jointly ac-
complish their task. In autonomous logistics, also
the second case occurs quite frequently (Schuldt and
Werner, 2007). Think, for instance, of an intelligent
package that intends to be transported from a ware-
house to a distribution centre. In principle, the pack-
age could achieve this objective on its own by nego-
tiating with a truck, also represented by an intelligent
agent, that takes over the transport. However, trans-
porting an individual package by truck is frequently
not cost-efficient. Instead, it is desirable that multiple
packages with the same origin and destination jointly
employ a truck in order to prevent a goal conflict re-
garding their cost-efficiency. Therefore, the important
task for autonomous logistics entities is to establish
teams based on joint properties such as a common lo-
cation and destination.
Apart from general interaction design principles
(Rosenschein and Zlotkin, 1994; Sandholm, 1999),
the requirements for team formation in this area of
application are as follows:
1. Unique teams
2. Flexible teams
3. Genericness
4. No prior knowledge
5. Decentralisation
6. Efficiency
The demand for unique teams means that only one
team should exist for each instantiation of a team
property. In terms of the above example, there should
only be one team of packages for each pair of ori-
gin and destination. This ensures the highest re-
source utilisation of the trucks employed. Of course,
each team can intentionally employ multiple trucks
if necessary. In other words, the requirement for
unique teams means that agents group themselves by
an equivalence relation with respect to one property.
Nevertheless, different properties and thus teams may
exist for different purposes, e.g., transport and stor-
age service allocation.
Furthermore, teams should be flexible in the sense
that additional members can join after the initial for-
mation. The method should be generic in that it is
not restricted to specific descriptors of properties. The
team formation mechanism should not make or only
make few requirements regarding prior knowledge
participants must have about the structure of the mul-
tiagent system and other participants. The approach
should be decentralised in order to prevent bottle-
necks, thereby still being efficient.
2.2 Related Work
Previous work on team formation focused on formal-
ising organisations of agents (Ferber and Gutknecht,
1998; Hannoun et al., 2000; Fischer et al., 2003)
as well as the internal states of agents during team
formation (Wooldridge and Jennings, 1999; Dignum
et al., 2000). Less effort has been spent on agent
interaction protocols for team formation. Previous
TEAM FORMATION FOR AGENT COOPERATION IN LOGISTICS - Protocol Design and Complexity Analysis
399
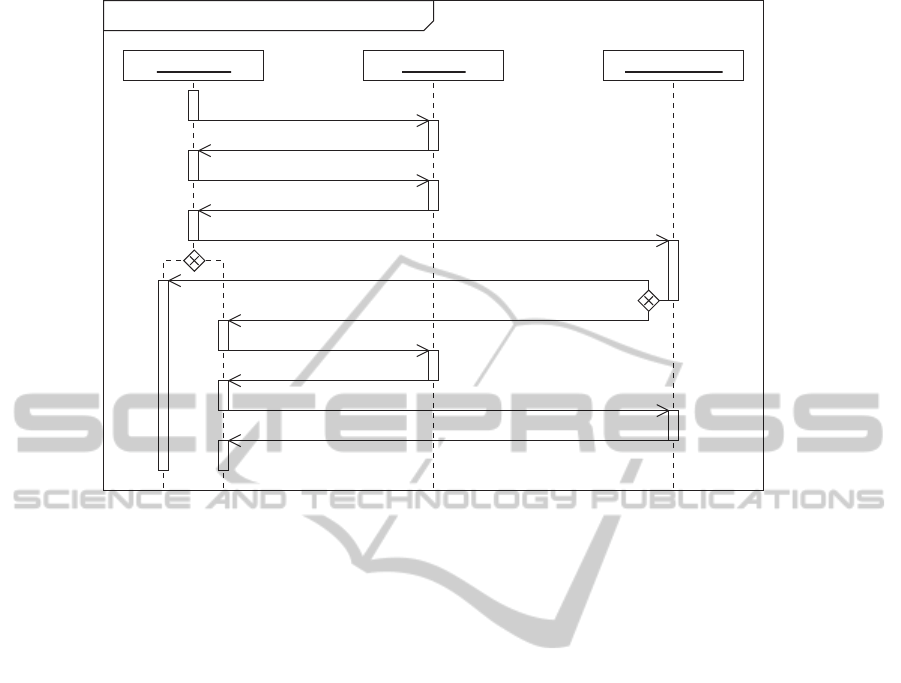
:Participant :Directory :TeamManager
n
n
m≤n
l=n-m
request-search-teams
inform-team-list
request-register
inform-registered
request-team-match
inform-team-match
failure-team-match
request-deregister
inform-deregistered
request-join-team
inform-team-joined
Optimistic-TeamFormationByDirectory-Protocol
Figure 2: Agent interaction protocol for team formation based on a directory service. Participating agents are optimistic in
that they initially assume that they can form a new team before possibly joining an existing one.
clustering algorithms such as k-means (MacQueen,
1967) take a centralised perspective on the data to be
clustered. This perspective, however, is usually not
available in the distributed setting of multiagent sys-
tems in general and autonomous logistics in particu-
lar. Hence, they cannot be applied.
Distributed clustering is, for instance, applied
in wireless sensor networks (Akyildiz et al., 2002).
However, these approachesare not applicable because
they focus on spatial data and thus make implicit
assumptions on the environment (Heinzelman et al.,
2000) that do usually not hold in autonomous logis-
tics. In particular, this contradicts the requirement for
generic descriptors.
Peer-to-peer approaches (Ogston and Vassiliadis,
2001) provide each agent with an arbitrarily cho-
sen set of other agents it is initially connected with.
Agents inform their peers about each other so that
they can exchange their direct partners by others
that are more similar. Unfortunately, this setting
is purely artificial for autonomous logistics because
autonomous logistics entities do not have any prior
knowledge about other agents in the systems. Conse-
quently, there is no natural choice for initial peers.
Often, the contract net (Smith, 1977) interaction
protocol is applied to implement team formation.
However, it only fits the case (Section 2.1) that an
agent aims at finding others that supplement its own
capabilities. In particular, the requirements for unique
and flexible teams are not met. It cannot be pre-
vented that teams with similar properties are estab-
lished. This is particularly because members cannot
join after a team has been established. This would re-
quire that team managers continuously advertise their
team to potential new members. The question, how-
ever, remains open what might be an appropriate fre-
quency for such announcements.
2.3 Team Formation Protocol
To summarise the discussion in Sections 2.1 and 2.2,
there is a demand for a new method for team forma-
tion. Figure 2 depicts an agent interaction protocol
that reflects the identified requirements. The proto-
col is based on a previous one (Schuldt and Werner,
2007). A comparison follows below.
The involved agent roles comprise the initiating
participant, the existing team managers, as well as a
directory service that administers the list of current
team managers. When an agent decides to participate
in the team formation process, it initially registers it-
self as a new team manager with the directory. This
behaviour is optimistic in that the participant assumes
that there is currently no team manager matching its
respective properties for team formation. In order to
check whether this assumption is actually true, it re-
quests the list of all current team managers from the
directory. Afterwards, it provides all team managers
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
400

with its own properties so that the managers can de-
termine whether their properties are matching. This
communication is done in parallel to be time-efficient.
The check conducted by the team managers has
three possible outcomes. Firstly, the match process
may fail for all team managers, i.e., no team matches
the properties of the new participant. In that case,
the initial assumption was right and the new partic-
ipant actually becomes a new team manager. Sec-
ondly, one team manager may determine a match. In
that case, the optimistic assumption turns out to be
wrong. Hence, the new participant deregisters from
the directory and joins the matching team instead. Fi-
nally, it might also occur that multiple team managers
determine a match. This is the case whenever mul-
tiple agents have concurrently registered with the di-
rectory with same properties. To resolve this problem
of redundant teams, each team manager is assigned an
individual timestamp when registering with the direc-
tory. Based on this timestamp, all agents including the
superfluous team managers can join the initial team.
As an alternative to the optimistic behaviour, it
would also be possible to act conservatively as it is
done in the ancestor of the protocol (Schuldt and
Werner, 2007). In the conservative case, new par-
ticipants would first contact all existing team man-
agers before registering themselves with the directory
service. Due to concurrency, however, still multiple
agents with same properties might register as team
managers. After the registration process, it would
therefore be necessary to contact the existing team
managers again in order to resolve redundancy. The
advantage of the optimistic procedure is thus that
team managers only have to be contacted once.
The requirements derived in Section 2.1 are re-
flected as follows. The proposed interaction proto-
col ensures that the resulting teams are unique. If
teams with identical properties are established, e. g.,
due to concurrency, this can be resolved by the pro-
tocol. Team formation is flexible because the partici-
pants and not the team managers initiate team forma-
tion, i. e., participants can join teams after initial es-
tablishment. The protocol is generic because it does
not restrict the possible descriptors for team proper-
ties. Furthermore, only few prior knowledge about
the system is required because participants can re-
trieve the list of existing team managers from the di-
rectory. The approach is decentralised in that all deci-
sions are made autonomously by the participants and
team managers. The only central entity and thus a po-
tential bottleneck is the directory. But the directory
service is not necessarily provided by only one agent.
Instead, it can be offered by multiple agents which co-
ordinate with each other internally (Bellifemine et al.,
2007). Regarding efficiency, the asymptotic interac-
tion complexity for team formation is O(mn) = O(n
2
)
from a coarse perspective. However, the number m of
team managers is usually only a small fraction of all
n participants, i. e., m ≪ n. A more detailed analysis
follows in the subsequent Sections 3 and 4.
3 INTERACTION COMPLEXITY
The analysis of the interaction effort for the proposed
team formation protocol is approached in two steps.
Section 3.1 examines the possible range of team con-
figurations for given sets of agents. Based on this
foundation, Section 3.2 presents the analytical exam-
ination of the team formation interaction effort.
3.1 Possible Team Configurations
As elaborated in Section 2.1, all agents in one team
are characterised by similar properties. Although
these properties may change over time, each agent has
specific properties at the time it initiates team forma-
tion. The task is thus to find the other agents with
the same properties. There exist numerous combi-
nations how intelligent agents can be partitioned into
similar properties and accordingly teams. The distri-
bution of agents to teams can be regarded as integer
partitions (Zoghbi and Stojmenovic, 1998). As an ex-
ample, the possible integer partitions of four are:
4 = 3 + 1 = 2+ 2 = 2+ 1+ 1 = 1 + 1 + 1+ 1 (1)
Thinking of four agents, they could all pertain to the
same team. Another possibility is that there is one
team of three agents and one singleton team and so
on. The possible partitions can be written as a set of
multisets:
{{(4, 1)}, {(3, 1), (1, 1)}, {(2, 2)},
{(2, 1), (1, 2)}, {(1, 4)}} (2)
More generally, the integer partitions for arbitrary nat-
ural numbers can be defined as follows:
Definition 1 (Integer Partitions). Let N ⊂ N be a set
of natural numbers, let M = (N, m) be a multiset over
N with m : N → N
+
defining the multiplicity of the
elements of N. M = (N, m) is a partition of s ∈ N if
∑
n∈N
n· m(n) = s. The set of all partitions of s into p
summands is
partitions(s, p)
:
=
(
(N, m)
∑
n∈N
m(n) = p∧
∑
n∈N
n· m(n) = s
)
TEAM FORMATION FOR AGENT COOPERATION IN LOGISTICS - Protocol Design and Complexity Analysis
401

The total set of all partitions of i is
partitions(s)
:
=
s
[
p=1
partitions(s, p)
Definition 1 is the foundation for examining the
possible partitions of integers into parts (van Lint and
Wilson, 1992) and agents into teams, respectively.
Fast algorithms exist that compute all possible inte-
ger partitions (Zoghbi and Stojmenovic, 1998).
3.2 Interaction Effort Analysis
As elaborated in Section 2.3, the asymptotic inter-
action complexity of the team formation protocol is
O(mn) = O(n
2
) from a coarse perspective. The ac-
tual interaction effort depends on two factors:
1. The total number of team managers
2. The times at which additional participants become
team managers
Every agent that joins the multiagent system contacts
all existing team managers to find a matching team.
To determine the interaction effort for a particular
agent, one must thus find out how many team man-
agers exist at its creation time. The question how
many agents in the multiagent system are team man-
agers at a certain point in time can be reformulated. It
is equivalent to the question to how many teams the
agents in the multiagent system pertain. The ques-
tions are interchangeable because the first agent of
each team is the responsible team manager.
The question of the number of teams can be ap-
proached in two steps. Firstly, one must determine
the probability that an agent of a particular team has
already been created. Secondly, the resulting proba-
bility must be accumulated for all teams to get the to-
tal number of different teams existing. A foundation
for this investigation is the hypergeometric distribu-
tion (Bronshtein et al., 2004). It is defined as follows:
Definition 2 (Hypergeometric Distribution). Let
A ∈ N be the size of the population, let T ≤ A ∈ N
be the number of successes in the population, let a ≤
A ∈ N be the number of draws, and let t ≤ A ∈ N be
the number of successful draws. The probability for t
given a, T, and A is
P(X = t)
:
= h(t |a, T, A) =
T
t
A−T
a−t
A
a
Let A denote the total number of agents. All
agents are numbered by a in the order of their cre-
ation. That is, a− 1 agents have been created before
agent a with 1 ≤ a ≤ A. Let T denote the number of
agents pertaining to a particular team. Based on Def-
inition 2, the probability that at least one member of
the team is in the total number of agents examined so
far can be derived as follows:
P(X > 0)
:
=
T
∑
t=1
h(t|a, T, A) = 1− h(0| a, T, A) (3)
Therewith, the question of the probability that at least
one agent of a team has already been created is an-
swered. The extension to all teams follows.
The respective partitioning of agents to teams, or
to properties to be more precise, can be considered an
integer partition (Definition 1). The respective parti-
tioning of all agents A is represented by the multiset
M = (N, m) ∈ partitions(A) (4)
Summing up the probabilities for the existence of in-
dividual teams (Equation 3) for all teams (Equation 4)
in the multiagent system reveals the number of al-
ready existing teams at the creation time of agent a:
f(a, (N, m), A)
:
=
∑
n∈N
m(n) ·
1− h(0| a, n, A)
(5)
To recapitulate, the number of teams corresponds to
the number of team managers agent a has to interact
with, i.e., it specifies the expected interaction effort
of agent a. The total interaction effort of the whole
system until the creation of agent a can be derived
from Equation 5 as follows:
F(a, (N, m), A)
:
=
a
∑
i=1
f(i, (N, m), A) (6)
=
a
∑
i=1
∑
n∈N
m(n) ·
1− h(0| i, n, A)
4 CASE STUDY
A considerably high number of possible agent parti-
tions into teams exists. Hence, following the general
analysis of the interaction effort for team formation,
this section investigates a particular configuration in
more detail. Out of the variety of possible partitions,
the case in which all teams have approximately the
same size is examined. This means that those parti-
tions M = (N, m) ∈ partitions(s) with the following
numbers of s agents into p teams are considered:
N =
s
p
,
s
p
(7)
The multiplicity m of the numbers of agents in M is:
m =
s
p
, p− (s mod p)
,
s
p
, s mod p
(8)
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
402

1
100
200
300
400
500
600
700
800
900
1000
Teams
600
1
100
200
300
400
500
700
800
900
1000
Agent
0
200
400
600
800
1000
1200
Interactions
0
200
400
600
800
1000
1200
Interactions
Figure 3: The number of interaction partners for participants in the team formation interaction protocol. The number of
interactions depends on the number of predecessors in the team formation process.
For the sake of understandability, the partition can
also be written as a sum. It corresponds to the fol-
lowing equation:
s =
s
p
· (p− (s mod p)) +
s
p
· (s mod p) (9)
Note that the remainder s mod p may be zero. Then,
the right element in the sets of Equations 7 and 8
is omitted. This is in accordance with Definition 1
which demands multiplicities to be positive. In this
case, all teams have the same number of agent mem-
bers. Otherwise, it holds that all teams have approxi-
mately the same number of agents, i. e., the difference
of the number of agents does not exceed one:
∀
n
1
,n
2
∈N
|n
1
− n
2
| ≤ 1 (10)
Figure 3 depicts Equation 5 for such average
teams for all 1 ≤ a ≤ A when varying the number of
teams 1 ≤ T ≤ A for a total of A = 1, 000 agents. Fig-
ure 4 shows the overall interaction effort for the same
team partitions investigated in Figure 3. Figures 3 and
4 have a different scale. The maximum interaction ef-
fort is 1, 000 for an individual agent and about half a
million for the whole system of 1, 000 agents.
5 PROTOCOL APPLICATION
The team formation interaction protocol is currently
applied in autonomous logistics applications, such as
autonomous onward carriage (Schuldt, 2010). In on-
ward carriage, containers arriving from overseas at
container terminals have to be transported to appro-
priate warehouses. In autonomous onward carriage,
intelligent shipping containers are expected to solve
this task on their own. To this end, they haveto choose
the warehouse based on their properties. For instance,
containers with valuable goods should choose a se-
cured warehouse. After having chosen a warehouse,
the containers must organise their transport by choos-
ing a means of transport out of truck, train, and barge.
The autonomous logistics approach has been im-
plemented with JADE (Bellifemine et al., 2007) and
validated with PlaSMA (Schuldt et al., 2008). For
evaluation purposes, real-world container data has
been provided by a major European retailer of con-
sumer products. Multiagent-based simulations with
over 11,500 shipping containers show that process
control can actually be delegated to autonomous lo-
gistics entities. In particular, it can be shown that
cooperation is advantageous in autonomous logistics
(Schuldt, 2010). Both choosing storage and trans-
port resources requires cooperation. Regarding stor-
age, containers with similar cargo should be received
in the same warehouse. This helps aggregating simi-
lar goods for subsequent distribution processes. Team
formation for this purpose requires establishing teams
based on descriptors for the articles loaded. Utilis-
ing means of mass transport requires cooperation by
shipping containers with same origin and destination.
Hence, spatial criteria have to be considered for this
purpose. This means that teams for allocating stor-
age and transport resources differ in this application
(Schuldt, 2010).
TEAM FORMATION FOR AGENT COOPERATION IN LOGISTICS - Protocol Design and Complexity Analysis
403

0
100000
200000
300000
400000
500000
600000
Interactions
0
100000
200000
300000
400000
500000
600000
Interactions
1
100
200
300
400
500
600
700
800
900
1000
Teams
600
1
100
200
300
400
500
700
800
900
1000
Agent
Figure 4: The total number of interactions for team formation. Depending on the number of teams, the interaction effort
ranges between linear and quadratic.
The simulation shows that the multiagent system
outperforms the previous approach in which humans
dispatch containers manually with support by infor-
mation systems. In particular, more relevant param-
eters can be considered, thereby increasing resource
utilisation efficiency for standard cases. Moreover,
being relieved from handling standard cases, human
dispatchers can solve exceptional cases which are not
covered by the multiagent systems more efficiently.
The thorough investigation of the interaction com-
plexity helped estimate the interaction effort even be-
fore deploying agents to an actual application. In par-
ticular, the interaction effort was estimated based on
previous container data. Therewith, it was possible to
decide that the exchanged messages can actually be
handled by the multiagent system and, thus, that au-
tonomous control is actually possible in this process.
6 CONCLUSIONS AND
OUTLOOK
This paper presents an interaction protocol for team
formation of autonomous logistics entities. The pro-
tocol satisfies the domain-specific requirements for
unique and flexible teams, as well as genericness of
team descriptors. Furthermore, it demands only min-
imal prior knowledge about the system and is highly
decentralised. Therewith, it lays important founda-
tions for cooperation of autonomous logistics entities
which in turn increase the reactivity and robustness of
logistics process control.
The motivation for the new protocol as well as its
current application are in the field of logistics. How-
ever, it is not restricted to logistics and can be applied
also in other areas with similar requirements. In terms
of the model for cooperation of intelligent agents, it is
particularly applicable whenever agents with similar
properties want to cooperate.
The interaction effort of the new protocol has been
derived analytically. This is an important prerequi-
site for estimating the effort and limitations for au-
tonomous control already before the actual deploy-
ment. A thorough analysis as provided in this paper is
necessary whenever the interaction effort is not obvi-
ous, e. g., if the number of participants changes over
time. Limitations of the protocol are reached when-
ever the interaction effort exceeds the capability of the
individual agents or the whole system. A solution for
such a case is to employ an interaction protocol with a
lower degree of decentralisation (Schuldt, 2010). An
alternative might be to restrict the number of partic-
ipants, for instance, based on spatial regions of rele-
vance (Gehrke, 2009).
ACKNOWLEDGEMENTS
The author should like to thank Hartmut Messer-
schmidt for helpful comments on the complexityanal-
ysis. This research is funded by the German Research
Foundation (DFG) within the Collaborative Research
Centre 637 “Autonomous Cooperating Logistic Pro-
cesses: A Paradigm Shift and its Limitations” (SFB
637) at the University of Bremen, Germany.
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
404

REFERENCES
Akyildiz, I. F., Su, W., Sankarasubramaniam, Y., and
Cayirci, E. (2002). Wireless Sensor Networks: A Sur-
vey. Computer Networks, 38(4):393–422.
Bellifemine, F., Caire, G., and Greenwood, D. (2007). De-
veloping Multi-Agent Systems with JADE. John Wiley
& Sons, Chichester, UK.
Bronshtein, I. N., Semendyayev, K. A., Musiol, G., and
Mühlig, H. (2004). Handbook of Mathematics.
Springer-Verlag, Heidelberg, Germany, 4th edition.
Chaib-draa, B. and Müller, J. P., editors (2006). Multiagent-
Based Supply Chain Management. Springer-Verlag,
Heidelberg, Germany.
Dignum, R., Dunin-Keplicz, B., and Verbrugge, R. (2000).
Agent Theory for Team Formation by Dialogue. In
ATAL 2000, pages 150–166, Boston, MA, USA.
Springer-Verlag.
Ferber, J. and Gutknecht, O. (1998). A Meta-Model for
the Analysis and Design of Organizations in Multi-
Agent Systems. In ICMAS 1998, pages 128–135,
Paris, France. IEEE Computer Society.
Fischer, K., Schillo, M., and Siekmann, J. H. (2003).
Holonic Multiagent Systems: A Foundation for the
Organisation of Multiagent Systems. In Holo-
MAS 2003, pages 71–80, Prague, Czech Republic.
Springer-Verlag.
Gehrke, J. D. (2009). Evaluating Situation Awareness of
Autonomous Systems. In Madhavan, R., Tunstel, E.,
and Messina, E., editors, Performance Evaluation and
Benchmarking of Intelligent Systems, pages 93–111.
Springer-Verlag, Heidelberg, Germany.
Hannoun, M., Boissier, O., Sichman, J. S., and Sayettat, C.
(2000). MOISE: An Organizational Model for Multi-
agent Systems. In IBERAMIA-SBIA 2000, pages 156–
165, Atibaia, Brazil. Springer-Verlag.
Heinzelman, W. R., Chandrakasan, A., and Balakrishnan,
H. (2000). Energy-Efficient Communication Protocol
for Wireless Microsensor Networks. In HICSS 2000,
volume 8, pages 8020–8029.
MacQueen, J. (1967). Some Methods for Classification and
Analysis of Multivariate Observations. In 5th Berkeley
Symposium on Mathematical Statistics and Probabil-
ity, pages 281–296, Berkeley, CA, USA. University of
California Press.
Ogston, E. and Vassiliadis, S. (2001). Matchmaking Among
Minimal Agents Withouta Facilitator. In Agents 2001,
pages 608–615, Montreal, QC, Canada. ACM Press.
Rosenschein, J. S. and Zlotkin, G. (1994). Rules of En-
counter: Designing Conventions for Automated Ne-
gotiation Among Computers. MIT Press, Cambridge,
MA, USA.
Sandholm, T. W. (1999). Distributed Rational Decision
Making. In Weiss, G., editor, Multiagent Systems.
A Modern Approach to Distributed Artificial Intelli-
gence, pages 201–258. MIT Press, Cambridge, MA,
USA.
Schuldt, A. (2010). Multiagent Coordination Enabling Au-
tonomous Logistics. Doctoral Dissertation, Univer-
sität Bremen.
Schuldt, A., Gehrke, J. D., and Werner, S. (2008). De-
signing a Simulation Middleware for FIPA Multiagent
Systems. In WI-IAT 2008, pages 109–113, Sydney,
Australia. IEEE Computer Society Press.
Schuldt, A. and Werner, S. (2007). Distributed Clustering
of Autonomous Shipping Containers by Concept, Lo-
cation, and Time. In MATES 2007, pages 121–132,
Leipzig, Germany. Springer-Verlag.
Smith, R. G. (1977). The Contract Net: A Formalism for
the Control of Distributed Problem Solving. In IJ-
CAI 1977, page 472, Cambridge, MA, USA. William
Kaufmann.
van Lint, J. H. and Wilson, R. M. (1992). A Course in Com-
binatorics. Cambridge University Press, Cambridge,
UK.
Windt, K. and Hülsmann, M. (2007). Changing Paradigms
in Logistics. In Hülsmann, M. and Windt, K., editors,
Understanding Autonomous Cooperation and Control
in Logistics, pages 1–16. Springer-Verlag, Heidelberg,
Germany.
Wooldridge, M. and Jennings, N. R. (1999). The Cooper-
ative Problem Solving Process. Journal of Logic &
Computation, 9(4):563–592.
Zoghbi, A. and Stojmenovic, I. (1998). Fast Algorithms for
Generating Integer Partitions. International Journal
of Computer Mathematics, 70(2):319–332.
TEAM FORMATION FOR AGENT COOPERATION IN LOGISTICS - Protocol Design and Complexity Analysis
405
