OPTIMIZING THE ASSESSMENT OF CEREBRAL

AUTOREGULATION FROM LINEAR

AND NONLINEAR MODELS

Natalia Angarita-Jaimes and David Simpson

Institute of Sound and Vibration Research, University of Southampton, Southampton, U.K.

Keywords: Cerebral Autoregulation, Linear and Non-linear system identification, Blood flow, Blood pressure,

Physiological modeling, Volterra-Wiener models, Wiener-Laguerre models.

Abstract: Autoregulation mechanisms maintain blood flow approximately stable despite changes in arterial blood

pressure. Mathematical models that characterize this system have been used in the quantitative assessment

of function/impairment of autoregulation as well as in furthering the understanding of cerebral

hemodynamics. Using spontaneous fluctuations in arterial blood pressure (ABP) as input and cerebral blood

flow velocity (CBFV) as output, the autoregulatory mechanism has been modeled using linear and nonlinear

approaches. From these models, a small number of measures have been extracted to provide an overall

assessment of autoregulation. Previous studies have considered a single – or at most- a couple of measures,

making it difficult to compare the performance of different autoregulatory parameters (and the different

modeling approaches) under similar conditions. We therefore compare the performance of established

autoregulatory parameters in addition to novel features extracted from the models’ response to a band-pass

filtered impulse. We investigate if some of the poor performance previously reported can be overcome by a

better choice of autoregulation parameter to extract from the model. Twenty-six recordings of ABP and

CBFV from normocapnia and hypercapnia in 13 healthy adults were analyzed. In the absence of a ‘gold’

standard for the study of dynamic cerebral autoregulation, lower inter and intra subject variability of the

parameters and better separation between normo- and hyper-capnia states were considered as criteria for

identifying improved measures of autoregulation. We found that inter- and intra- subject variability in the

assessment of autoregulation can be significantly improved by a careful choice of autoregulation measure

extracted from either linear or non-linear models.

1 INTRODUCTION

The active control of the diameter of small blood

vessels in the brain, usually referred to as cerebral

autoregulation (CA), protects the brain against injury

due to insufficient or excessive blood flow resulting

from a temporary drop or surge in arterial blood

pressure (ABP). Autoregulation is of great clinical

interest as it can be impaired or lost in a number of

conditions, such as stroke and subarachnoid

haemorrhage (Panerai, 1998, Panerai, 2007). In

much of the published literature, blood flow is

recorded by the safe and non-invasive Doppler

ultrasound method in response to transient changes

in ABP. Sudden deflation of a thigh cuff, large

sinusoidal variations in lower-body negative

pressure, periodic breathing or squatting, and the

Valsalva maneuver have been used to provoke larger

changes in ABP (Panerai, 1998). However the most

desirable experimental protocol for assessing

autoregulation is to record data from patients at rest

(without performing any specific maneuvers or

requiring active collaboration), especially if they are

in intensive care. Thus, many recent studies have

focused on using only spontaneous fluctuations of

ABP. While this approach increases challenges in

terms of analyzing the recorded signals and can lead

to high intra- and inter-subject variability, its

effectiveness has been demonstrated (Panerai, 1998,

Panerai et al., 1998, Panerai, 2007, among others).

Algorithms already described in the literature for

estimating autoregulation involve system

identification (black-box modeling) to represent the

relationship between ABP and CBFV. Most of the

studies of autoregulation focus on linear methods

(Zhang et al., 1998, Birch et al., 1995, Panerai et al.,

1999, 2003, Simpson et al., 2001) with the more

recent inclusion of some nonlinear approaches

251

Angarita Jaimes N. and Simpson D..

OPTIMIZING THE ASSESSMENT OF CEREBRAL AUTOREGULATION FROM LINEAR AND NONLINEAR MODELS .

DOI: 10.5220/0003164902510256

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2011), pages 251-256

ISBN: 978-989-8425-35-5

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

(Panerai et al., 1999, Marmarelis et al., 2002,

Panerai et al., 2004, Angarita-Jaimes et al., 2010).

Although nonlinear techniques can provide

improved model fits, their benefit in assessing

cerebral autoregulation is still unclear with few

studies having systematically compared them to

linear alternatives.

In the investigation of autoregulation from linear

models, the extraction of a small number of

parameters from the frequency-, the impulse- or

step-response of the models have been studied.

Examples of autoregulatory parameters include gain,

phase and coherence in selected frequency ranges,

(Zhang et al., 1999, Panerai et al., 1999, Birch et al.,

1995, Liu et al., 2003), selected features of the step-

response (e.g. slopes, amplitudes at selected points)

(Simpson et al., 2001, Liu et al., 2003). Alternative

methods include the autoregulatory index (ARI)

(Tiecks et al., 1995), or the correlation of the ABP

and CBFV time series (Piechnik et al., 1999). The

majority of published studies have only considered a

single -or at most- a couple of measures for the

analysis of cerebral blood flow control from

spontaneous variations (Liu et al., 2003, Panerai et

al., 2001, among others) and no single method for

assessing autoregulation has become accepted as a

gold standard..

The current paper aims to contribute to

optimizing this last, but crucial step in detecting

impairment in patients’ autoregulation from the

recorded signals. In this study, we investigate the

performance of both linear and nonlinear models,

and compare different measures extracted from the

models to assess cerebral autoregulation. In the

absence of a gold standard, the autoregulatory

parameters are evaluated on a sample of signals

recorded from healthy volunteers in whom

temporary impairment of autoregulation was

induced by hypercapnia. Based on the results, we

suggest some autoregulatory measures that are most

promising for future physiological and clinical

studies.

2 METHODS

2.1 Data Collection and Pre-processing

The study was performed on 13 healthy volunteer

subjects (age 32 ± 8.8 years) and was approved by

the local Research Ethics Committee. All recordings

were made with subjects in the supine position with

the head elevated. Middle cerebral artery velocity

was measured using a Transcanial Doppler

Ultrasound system (Scimed QVL-120) in

conjunction with a 2MHz transducer held in position

by an elastic headband. Simultaneously arterial

blood pressure (ABP) was non-invasively monitored

using a finger cuff device (Ohmeda 2300 Finapress

Bp monitor). End-tidal CO2 (EtCO2) levels were

monitored via an infra-red capnograph (Datex

Normocap 200). The experimental protocol for CO2

reactivity test was as follows: each recording began

with a period of breathing ambient air for

approximately 5 minute, followed by 2 minutes of

elevated (EtCO2 ) due to the inhalation of 5% CO2

in air.

The signals were pre-processed off-line. The

maximum velocity envelope from the spectra of the

Doppler signal was extracted by fast Fourier

transform (FFT) every 5 ms. The ABP signals were

digitized at 200 Hz. Short periods of evident artifact

as well as any spikes on the signals were removed

by linear interpolation. The ABP and CBF signals

were low pass filtered (20 Hz). The start of each

heart cycle was automatically identified from the

ABP signal, after which the average ABP and

CBFVs from the right and left MCA were calculated

for each heartbeat. This time series was then

interpolated with a third-order polynomial, and

sampled at a constant rate of 5 Hz. In order to reduce

the serial correlation between samples, the signals

were further decimated to a new sampling rate of

1Hz, following anti-alias filtering with a cut-off

frequency at 0.5 Hz. These recordings were

normalized by their mean values, and the mean

values of the resultant signals were then removed. In

that way, the relative change in each signal was

obtained, and will be denoted by %ABP and

%CBFV, respectively.

Figure 1: Representative recording, showing%ABP and

%CBFV. A phase lead of CBFV indicates a good cerebral

autoregulatory response.

2.2 Data Analysis

For each subject a segment of data was selected

from before (normocapnia – NC) and during 5%

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

252

CO2 breathing (hypercapnia – HC). The former

were approx. 300 s long and the latter approx. 100 s.

For both linear and nonlinear models, %ABP

was the input and %CBFV the output. Since both

signals are normalized, the underlying assumption is

that in the absence of autoregulation changes in

%CBFV would passively follow those in %ABP

(Panerai et al., 1999). All models were estimated

according to the usual least-mean-squares approach.

A linear sixth order (5 seconds in duration) FIR filter

(Liu et al., 2005) was chosen, since the

autoregulatory response is largely completed during

this time (Panerai et al., 2003, Liu et al., 2003). A

non-linear Volterra-Wiener model, as previously

proposed (Mitsis et al., 2003, Panerai et al., 1999,

Panerai et al., 2003), was also estimated using the

Wiener-Laguerre estimation procedure (for more

details see for example Panerai et al., 1999). The

number of lags used for both the linear and nonlinear

kernels was 12.

3 ASSESMENT OF CEREBRAL

AUTOREGULATION

3.1 Selection of Autoregulatory

Parameters

A commonly used approach (Panerai et al., 1999,

Panerai et al., 2003, Liu et al., 2005) to assess

cerebral autoregulation is to look at the final value of

the models response after applying an idealized step.

From physiology, the step response is expected to

first show a sharp increase in flow when blood

pressure rises, followed by a return towards baseline

within a few seconds as autoregulation provokes

arteriolar vasoconstriction. In the absence of

autoregulation, %CBFV would remain elevated.

However, the step response shows large variability

across subjects as well as erratic variations and

decays to values less than zero that are hardly

compatible with physiology (Simpson and Birch,

2008, Liu et al., 2005) – see Fig. 2A. The relatively

narrow frequency range of spontaneous oscillations

in blood pressure is expected to lead to poor

estimation of the frequency response in the very low

and very high frequencies where the system is not

excited. This in turn probably causes the wide spread

in the final values of the step responses and the

erratic rapid variations respectively (Figure 2).

Simpson and Birch (2008) therefore proposed an

alternative test-input to assess model responses.

Instead of the step, a cosine wave modulated by a

Gaussian envelope (Fig. 2B and Fig. 3) was chosen.

This pulse reflects more closely the characteristics of

ABP from spontaneous fluctuations and its shape is

visually similar to fluctuations observed in

spontaneously varying ABP signals.

Figure 2: Step (a) and pulse (b) response for thirteen

subjects estimated from a 5 seconds-long FIR model. The

inputs are shown as the bold-dotted line. Considerably

larger dispersion is observed in the step compared to the

pulse response.

In order to quantify autoregulation using this

response, , four parameters were selected, as shown

in Fig. 3: the time of the left shift of the response

(TLS, in seconds), measured as the difference in

time between input and output crossing the abscissa

after the main peak, the amplitude of the pulse

response at 1.5 seconds (A1.5), the amplitude at 6

seconds (A6) and the time of the second negative

peak (TP) - for the input signal this occurs at 3.5

seconds. These parameters were chosen as they

reflect the expected left-shift (phase-lead) of the

autoregulatory response, and had been found most

robust in preliminary work; A1.5 and A6 lie on the

steep slopes of the descending and ascending

responses, and are therefore likely to be most

sensitive to temporal shifts in the response.

We compare these novel parameters with others

previously proposed in the literature. First, we

estimated the final value of the step response (FVS)

for both the linear and nonlinear models. Then, for

-10 0 10

-3

-2

-1

time (s)

Input

Output

TLS

A1.5

Figure 3: The %ABP test input (dotted line - sinusoid

modulated by a Gaussian pulse) and the estimated

response (solid line - %CBFV), together with the

parameters used to quantify autoregulation.

OPTIMIZING THE ASSESSMENT OF CEREBRAL AUTOREGULATION FROM LINEAR AND NONLINEAR

MODELS

253

the linear models, the average phase (Pha) was

calculated from transfer function analysis in the

frequency range from 0.07 Hz to 0.2 Hz (Zhang et

al., 1998, Birch et al., 1995), and coherence, (Coh)

was evaluated over a similar range (Zhang et al.,

1998, Panerai et al., 1998). The correlation method

(Mx) was also estimated from the average Pearson’s

correlation coefficient of 4 equal segments of the

%ABP and %CBFV time series (Piechnik et al.,

1999). The Autoregulatory Index ARI was

calculated from the set of models proposed by

Tiecks et al. (1995). For each recording, the set of

models was applied to the %ABP, and the model

leading to the highest correlation coefficient

between the model generated velocity and the

measured %CBFV gave the ARI. Finally, a

parametric model based on the coefficients of a first-

order (two taps) FIR filter was evaluated. The

second coefficient of the filter H1 was selected as it

has been shown to reflect autoregulatory activity

(Simpson et al., 2001).

3.2 Statistical Analysis

The aim of estimating autoregulatory parameters is

to be able to distinguish between impaired and

normal autoregulation. Since hypercapnia is known

to impair autoregulation, changes in the

autoregulatory parameters in response to increased

pCO

were tested using Wilcoxon matched pairs

tests. In addition repeatability and intra- and inter-

subject variability were also evaluated. Inter-subject

variability was assessed by calculating the standard

deviation during normo and hypercapnia, and

averaging the result (SD). In order to compare the

performance of parameters, SD was normalized by

the difference in mean value between NC and HC

(CVd).

To investigate the effect of noise and as an

indication of the repeatability of the autoregulatory

parameters, 100 simulated signals were generated

from each of the recordings. Additive noise was

modeled based on the residual error in %CBFV (i.e.

the signal component that cannot be explained by

applying the identified models to the %ABP signals)

using an AR model of order 8. Surrogate %CBFV

signal were then generated by applying the identified

models (linear or nonlinear) to the %ABP signals

and then adding the random noise to simulate

residuals. Autoregulation parameters were then

calculated from these simulated signals, and their

standard deviation was considered as the intra-

subject variability for each recording and parameter.

These were also normalized by the parameter’s

mean difference between normocapnia and

hypercapnia, and their average across the subjects

was denoted by mCVd. Low values of CVd and

mCVd indicate low dispersion and wide separation

between groups.

For each model, the predicted velocity response

was also compared to the measured data and the

model’s performance was evaluated using the

normalized mean square error (NMSE). Cross-

validation, with two equal segments, was used to

calculate NMSE.

4 RESULTS

Table 1 shows the NMSE in fitting different models

to the data. The most sophisticated model has the

smallest error on the training data (150 s duration)

but on the validation data set performs poorly. The

simplest model (1

order FIR) overall shows the

poorest model fit, both on training and validation

data.

Table 1: Mean ± SD NMSE across 13 subjects for the

different models used on baseline recordings.

The performance of the different autoregulatory

parameters is shown in Figure 4, and provides a

rather different picture of which model might be

most appropriate in quantifying autoregulation. CVd

and mCVd estimates, indicating inter- and intra-

subject variability respectively, are presented for all

10 parameters studied. The last five were evaluated

for both the linear (L) and nonlinear models (NL).

Autoregulatory parameters with the smallest

CVd indicate best separation between NC and HC,

and can thus considered to provide the clearest

distinction between normal and impaired

autoregulation in terms of inter-subject variability.

Amongst the parameters studied H1, TP (both for

linear and nonlinear models), A1.5 (linear model)

and A6 (nonlinear model) had the lowest CVd. The

latter three show a clear improvement compared to

the final value obtained from the step response

(FVS). Furthermore, Wilcoxon matched pair test

showed that the magnitude of these parameters

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

254

Mx Pha Coh ARI H1 L NL L NL L NL L NL L NL

100

120

140

160

180

FVS

A1.5

TLS

CVd

Inter-subject variability

mCVd

Intra-subject variability

Autoregulatory Parameter

Figure 4: Comparison of the different autoregulatory parameters. L (linear) and NL (non-linear) models, respectively. The

different significance levels of the Wilcoxon test comparing parameters during NC and HC are grouped as: + 0.009<p <

0.0009; * 0.09< p ≤ 0.009, o p≤0.09 (inter-subject variability) The parameters showing the strongest distinction between

NC and HC for linear and non-linear models, are circled.

changed significantly between NC and HC (H1,

p≈0.0014; TP-L, p≈0.0006; TP-NL p≈0.002, A1.5-

L p≈0.004; A6-NL p≈0.0006).

The different measures performed differently

depending on the models used to characterize the

relationship between ABP and CBFV. For example,

whilst the amplitude at 1.5 s or TLS performed well

with the L model, these had very high inter-

individual dispersion for the NL approach.

Conversely, amplitude at 6 s was the best parameter

for the NL and poorer for L. A slight improvement

in FVS was observed by using the NL approach.

When evaluating the influence of additive noise

in the recordings, the highest dispersion in terms of

mCVd (see Figure 4, darker bar) was noted for the

non-linear models, and especially the time-delay

parameters. In some cases the mCVd was larger than

CVd, which probably reflects the differences in

normalization: in the former dispersions are

normalized by the differences for each individual

(and then averaged across the cohort), but in the

latter it normalization is by the average difference.

Conventional parameters extracted from the

frequency response (Pha, Coh) as well as Mx were

relatively robust to noise (low mCVd). Overall, the

autoregulatory parameters with the lowest variability

and best separation between pC02 levels are H1,

A1.5 (linear model) and A6 (nonlinear model). The

excellent performance of the simplest parameter,

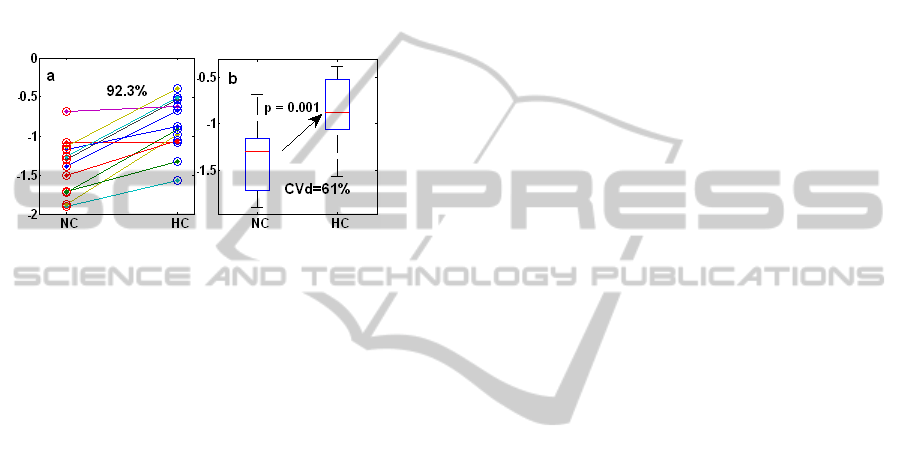
H1, is particularly notable, and is shown in more

detail in Figure 5, with 12 of 13 subjects showing

the expected increase in H1 during HC.

5 DISCUSSION

In previous work, the high inter-subject variability

of a number of measures of cerebral blood flow

control and poor repeatability has been noted

(Panerai et al., 2003, Simpson et al., 1999). The

results in this work showed that the model used to

represent the relationship between blood flow and

blood pressure, and how the models are then used

(the calculation of autoregularory parameters), can

notably increase the uncertainty in the estimates.

The current work is probably the most extensive

comparison between different parameters of

autoregulation published to date. In some of the

earlier work (Panerai et al., 1999, Panerai et al.,

2003, Mitsis et al., 2004, Angarita-Jaimes et al.,

2010) the primary concern has been with how well

different models fit the data. This however is only an

intermediate step in addressing the main challenge:

quantifying autoregulation when only spontaneous

fluctuations in ABP and CBFV are present. In the

continued absence of a gold-standard measure of

autoregulation, we take as criteria for assessing

performance the ability to distinguish between

normal (during normo-capnia) and impaired (during

hyper-capnia) autoregulation. The current work also

moves beyond the more established ‘test inputs’ that

give impulse, step or frequency (i.e. sine-wave)

responses, recommending a ‘test input’ that is

physiologically more realistic, in the form of a

broad-band pulse.

Larger dispersion was observed in the traditional

autoregulatory parameters, particularly in the final

OPTIMIZING THE ASSESSMENT OF CEREBRAL AUTOREGULATION FROM LINEAR AND NONLINEAR

MODELS

255

value of the step response, compared to some of the

measures extracted from the pulse response, as

indicated by CVd (see Figure 4). The simulations

indicate that intra-subject variability, due to assumed

additive noise in the recordings is a large contributor

the overall dispersion in results. However in this

respect, H1 outperformed all other measures. H1

was also among the best in terms of inter-subject

variability. It should also be noted that model fit

(Table 1) alone clearly is not a good indicator of

what makes for the best method in the assessment of

autoregulation.

Figure 5: a) Magnitude of H1 during normocapnia (NC)

and hypercapnia (HC). b) Box plots representation of the

median, quartile, minimum and maximum of H1.

A number of other parameters for assessing

autoregulation, including parameters taken directly

from the model (as H1 for the first order FIR filter)

were also investigated, but none proved superior to

the ones presented. The relatively small sample of

recordings available and relatively large number of

parameters tested is a limitation of the current study.

It is possible that the relative performance of the

methods reflects peculiarities or random effects in

the particular data set available. Given that

parameters estimated are not independent, the usual

methods for determining statistically significant

differences between the approaches are not

appropriate. However, the large differences observed

between methods, probably do indicate which

approaches are most promising to be taken on in a

further study on a larger data set.

6 CONCLUSIONS

In this work we have compared a number of

measures to evaluate autoregulatory activity. Some

of the parameters extracted from the proposed pulse

input show less variability compared with the more

conventional parameters extracted from the

frequency and step responses. Thus relatively small

variations across as well as within subjects were

found for the amplitude of the pulse response at

certain lags (A1.5, A6). These also showed a clearer

distinction between the different levels of

autoregulation (quantified by the p value). In

particular, for linear models A1.5 would be

recommended whereas A6 seemed to perform well

for nonlinear models. However, the results obtained

from H1 suggest that this parameter from a very

simple model might be the method of choice, with

small coefficients of variation (CVd, mCVd). This

method also allows the analysis of relatively short

data segments and thus lends itself to further studies

of time-varying (adaptive) estimates of dynamics in

cerebral blood flow control.

ACKNOWLEDGEMENTS

We would like to thank Drs. Stephanie Foster and

Lingke Fan and Prof. David Evans (Leicester Royal

Infirmary) for generously providing the anonymized

data used in this study and Innovation China UK for

funding support.

REFERENCES

Aaslid, R. et al., 1989 Cerebral autoregulation dynamics

in humans. Stroke, 20:45-52.

Angarita-Jaimes, N. et al., 2010. Nonlinear modelling of

CA using cascade models. Proc. Medicon 2010,

Greece.

Birch, A. et al., 2002. The repeatability of CA using

sinusoidal lower -ve pressure. Phys. Meas, 23,73-83

Liu, Y. et al., 2003 Dynamic cerebral autoregulation

assessed using an ARX model. Med. Eng. Phys., 25.

Liu, J. et al., 2005. High spontaneous fluctuation in ABP

improves the assessment of CA. Physiol. Meas, 26

Mitsis, G. et al., 2004 Nonlinear modelling of dynamic

CBF in healthy humans. Adv Exp Med Biol. 551:259-

265.

Panerai, R. et al., 1998. Grading of CA from spontaneous

fluctuations in ABP. Stroke, 29:2341-2346.

Panerai, R. 1998. Assessment of CA in humans -a review

of measurement methods. Physiol.Meas. 19.

Panerai, R. et al., 1999. Linear and nonlinear analysis of

human dynamic CA. Am J Heart Circ Physiol. 277

Panerai, R. et al., 2003. Variability of time-domain indices

of dynamic CA Physiol Meas, 24:367–381.

Piechnik, S. et al., 1999 The continuous assessment of

cerebrovascular reactivity Anesth Analg, 89:944–9

Simpson, D. et al., 2001. A parametric approach to

measuring CA Ann Biomed Eng, 29:18–25.

Simpson, D. and Birch, A., 2008. Optimising the

assessment of CA from black-box models. Proc.

MEDSIP 2008.

Tiecks, F. et al., 1995. Comparison of static and dynamic

CA measurements. Stroke 26: 1014-1019.

Westwick, D. and Kearney, R., 2006. Identification of

Nonlinear Physiological Systems. IEEE Press, 1st Ed.

Zhang R et al., 1998 Transfer function analysis of dynamic

CA in humans. Am. J. Physiol., 274.

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

256