
TWO-MODES CYCLIC BIOSIGNAL CLUSTERING BASED
ON TIME SERIES ANALYSIS
Neuza Nunes, Tiago Araújo
Physics Department, FCT-UNL, Lisbon, Portugal
Hugo Gamboa
Physics Department, FCT-UNL, Lisbon, Portugal
PLUX – Wireless Biosignals, Lisbon, Portugal
Keywords: Biosignals, waves, Unsupervised learning, Clustering, Data mining, Signal-processing.
Abstract: In this paper we introduce an unsupervised learning algorithm which distinguishes two different modes in a
cyclic signal. We also present the concept of “mean wave” which averages all signal waves aligned in a
notable point (n
th
zero derivative). With that information the signal’s morphology is captured. The clustering
mechanism is based on the information collected with the mean wave approach using a k-means algorithm.
The algorithm produced is signal-independent, and therefore can be applied to any type of signal providing
it is a cyclic signal that has no major changes in the fundamental frequency. To test the effectiveness of the
proposed method, we acquired several biosignals (accelerometry, electromyography and blood volume
pressure signals) in the context tasks performed by the subjects with two distinct modes in each. The
algorithm successfully separates the two modes with 99.2% of efficiency. The fact that this approach
doesn’t require any prior information and the preliminary good classification performance makes this
algorithm a powerful tool for biosignals analysis and classification.
1 INTRODUCTION
Human-activity tracking techniques focus on direct
observation of people and their behavior. This could
be done, as an example, with cameras (Jezekiel Ben-
Arie, 2002), accelerometers to track human motion
(Jonghun Baek et al., 2004), or contact switches to
compute facial expressions with the
electromyography patterns (Joshua R. Smith, 2005)
(Alan J. Fridlund, 2007).
In this work we acquired several cyclic
biosignals – such as accelerometry (ACC),
electromyography (EMG) and blood volume
pressure (BVP) signals – from subjects performing
some context tasks, and we’ve developed
an unsupervised learning algorithm which is capable
to distinguish two different modes in the same
acquired signal.
The developed algorithm follows an
unsupervised learning approach, as it doesn't require
any prior information (Zoubin Ghahramani, 2004).
We use the k-means cluster algorithm due to its
efficiency and effectiveness (Xindong Wu, 2007).
As a clustering method, our algorithm is signal-
independent and doesn’t use specific information
about the signals. Although our algorithm is signal-
independent, the signals used must be cyclic signals,
with only two distinctive modes and a small
variation of fundamental frequency between those
modes.
Warren Liao (2005) presents a survey on time
series data clustering, exposing past researches on
the subject. He organizes the works in three groups:
whether they work directly with the raw data,
indirectly with features extracted or indirectly with
models built from the raw data. We created a
different algorithm as we intended to work with
single signals with different modes or activities in it,
and the previous studies uses various signals each
one distinct with only one mode or activity.
A more resemble approach, as the clustering is
based on the similarity of wave shapes presented in a
single time series data, is the work of Dr. Rodrigo
Quiroga (2007) with spike sorting. However, as the
257
Nunes N., Araújo T. and Gamboa H..
TWO-MODES CYCLIC BIOSIGNAL CLUSTERING BASED ON TIME SERIES ANALYSIS .
DOI: 10.5220/0003165002570264
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2011), pages 257-264
ISBN: 978-989-8425-35-5
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)
neuron activity is not periodic, the spikes are
detected with a threshold and the clustering
procedure uses features extracted from those parts of
the signal.
We present the concept of “mean wave” which
averages all signal waves aligned in a notable point,
that we call triggering point, such as maximum,
minimum, zero or inflexion point. Our algorithm
automatically separates each signal’s cycle and
computes the mean wave using an alignment on the
triggering point of each cycle. With that information
the signal’s morphology is captured. Our clustering
algorithm uses the signal’s cycles information
gathered from the mean wave approach to separates
the two modes cycles of the entire signal.
As our mean wave approach effectively captures the
morphology of a signal, can be useful in several
areas – as a clustering basis or just for a simple
signal analysis.
In the following section the signal acquisition
methodology is presented. In section 3 we expose
the signal processing detailing all algorithms steps.
Finally in sections 4 and 5 we detail and discuss our
results and algorithm performance, concluding the
work.
2 METHODS
2.1 Acquisition System and Sensors
To acquire the biosignals necessary to this study we
used a surface electromyography (EMG) sensor,
emgPLUX, a triaxial accelerometer (ACC),
xyzPLUX, and a finger blood volume pressure
(BVP) sensor, bvpPLUX (bioPLUX Research
Manual, 2010).
For the signal’s analog to digital conversion and
bluetooth transmission to the computer we used a
wireless signal acquisition system, bioPLUX
research, which has 12 bit ADC and a sampling
frequency of 1000 Hz (bioPLUX Research Manual,
2010). In the acquisitions with accelerometers just
the axis with inferior-superior direction was
connected to the bioPLUX.
2.2 Data Acquisition and Data Format
Several tasks were designed and executed in order to
acquire signals that had two distinctive modes.
We conceived a synthetic digital signal and
collected signals from four different activities
scenarios with the accelerometer sensor, and one for
each EMG and BVP sensors.
2.2.1 Synthetic Signal
To test our algorithm, a synthetic wave (Figure 1)
created using a low-pass filtered random walk (of
100 samples), with a moving average smoothing
window of 10% of signal’s length, and multiplied by
a hanning window, was repeated 30 times, so all the
cycles were identical. After a small break on the
signal the wave was repeated 20 more times, with an
identical small change of 40 samples in all waves,
creating a second mode.
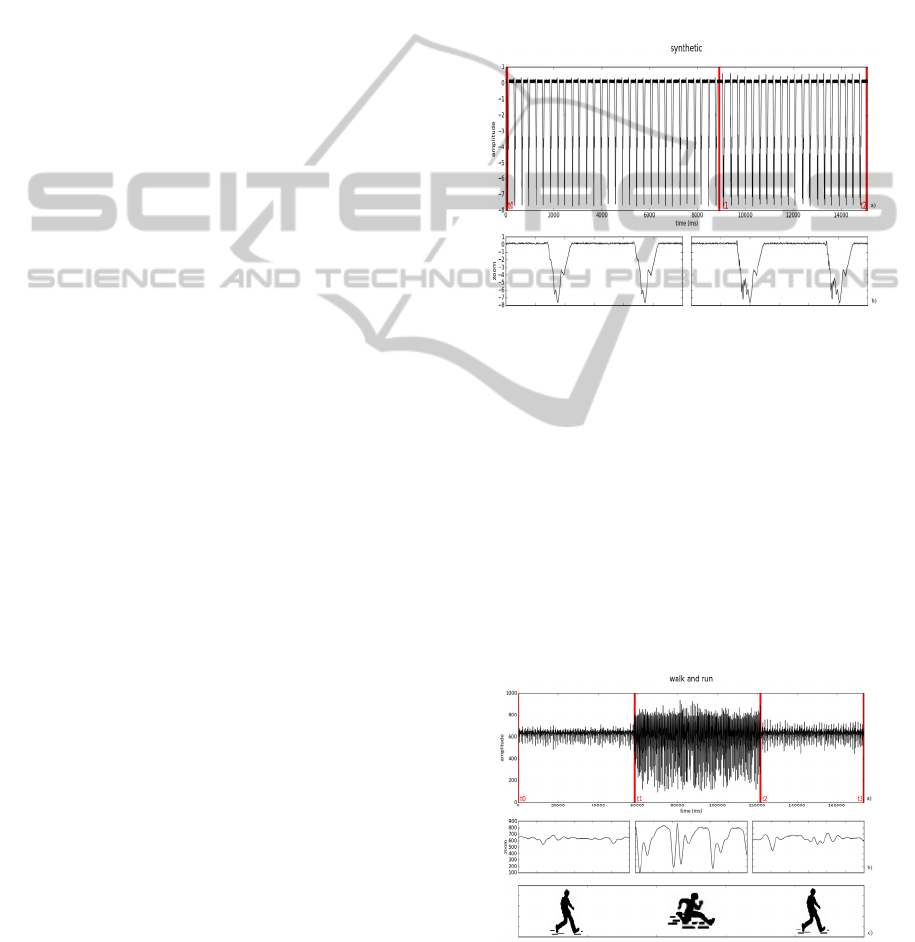
Figure 1 a): Synthetic signal with identical waves from t0
to t1 and from t1 to t2; b): corresponding zoomed waves.
2.2.2 Walking and Running (ACC)
With an accelerometer located at the right hip and
oriented so the y axis of the accelerometer (the only
connected to the bioPLUX) was pointing upward,
the subjects performed a task of walking and
running non-stop (on a large circle drawn on the
floor).
The subjects walked for about 1 minute at a slow
speed, then spent 1 minute running, and ended with
1 minute walking again. The signal acquired is
represented in figure 2.
Figure 2 a): Acceleration signal of walking (t0 to t1 and t2
to t3) and running (t1 to t2); b): corresponding zoomed
waves; c): tasks performed.
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
258

2.2.3 Running and Jumping (ACC)
With an accelerometer located at the right hip and
oriented so the y axis of the accelerometer (the only
connected to the bioPLUX) was pointing upward,
the subjects performed a task of running non-stop
(on a large circle drawn on the floor) and jumping
also continuously but at the same place.
The subjects spent 1 minute running, followed by
1 minute jumping. The signal acquired is
represented in figure 3.
Figure 3 a): Acceleration signal of running (t0 to t1) and
jumping (t1 to t2); b): corresponding zoomed waves; c):
tasks performed.
2.2.4 Jumping with and Without Impulsion
(ACC)
In this task, the following procedure was executed:
14 seconds of “normal” jumping (small jumps
without a big impulsion), 24 seconds of jumping
with some boost and again 7 seconds of normal
jumping.
The subjects used an accelerometer located at the
right hip and oriented so the y axis of the
accelerometer (the only connected to the bioPLUX)
was pointing upward. The signal acquired is
represented in figure 4.
2.2.5 Skiing (ACC)
Figure 5 shows the acceleration signal of an
accelerometer attached to the ski pole, below the
handgrip, used by the subject when skiing.
In the 37 seconds of the signal the subject
performed two different techniques, called V1 and
V2. V1 skate is an asymmetrical uphill technique
involving one poling action over every second leg
stroke. V2 skate is used for moderate uphill slopes
and on level terrain, involving one poling action for
each leg stroke. (Erik Andersson, 2010)
Figure 4 a): Acceleration signal of normal jumps (t0 to t1
and t2 to t3) and jumps with boost (t1 to t2); b):
corresponding zoomed waves; c): tasks performed.
Figure 5 a): Acceleration signal of skiing with V2
technique (t0 to t1 and t2 to t3) and skiing with V1
technique (t1 to t2); b): corresponding zoomed waves; c):
tasks performed.
The first 7 cycles of the signal (about 5 seconds)
were produced through a V2 technique, the next 27
cycles (about 25 seconds) a V1 technique and the
final 8 cycles the technique was V2 again.
2.2.6 Elevation and Squat of the Legs
(EMG)
The subject was standing straight with both feet
completely on the ground and was asked to
performed 12 elevations of the legs - getting on the
tiptoes and back with both feet completely on the
ground - followed by 11 squats - bending the knees
and back standing straight - (Figure 6). The EMG
data were collected using bipolar electrodes at the
gastrocnemius muscles of the right leg.
TWO-MODES CYCLIC BIOSIGNAL CLUSTERING BASED ON TIME SERIES ANALYSIS
259

Figure 6 a): EMG signal of the gastrocnemius muscle’s
contraction through the elevation (t0 to t1) and squat (t1 to
t2) of the inferior members; b): corresponding zoomed
waves; c): tasks performed.
2.2.7 Normal (at rest) and High Beat (after
Exercise) Signal (BVP)
The subjects were instrumented with a BVP sensor
on the fourth finger of the left hand and were seating
with his left forearm resting on a platform.
We’ve made one acquisition with the subject at
rest. The subjects performed intensive exercise that
was not collected to avoid undesirable artefacts due
to movement. After the exercise, we acquired
another BVP signal.
For the purpose of this study we used both
signals (at rest and after exercise) in the same file,
cutting a part of each signal and concatenating them
offline. The resulting signal is represented in figure
7.
Figure 7 a): BVP signal with the subject at rest (t0 to t1)
and after exercise (t1 to t2); b): corresponding zoomed
waves; c): tasks performed.
All the signals referenced above are available at
OpenSignals (Opensignals.net website, 2010).
3 SIGNAL PROCESSING
The collected data was processed offline using
Python with the numpy (T. Oliphant, 2006) and
scipy (T. Oliphant, 2007) packages.
Signal processing algorithms were developed for
automatic detection of a mean wave representative
of the signal’s behavior and the k-means algorithm
was used to cluster the signals. The main idea of this
algorithm is to define a loop with k centroids far
away from each other, take each point belonging to a
given data set and associate it to the nearest centroid.
Repeating the loop, the centroids position will
change because they are re-calculated as barycenters
of the clusters result, and after several iterations the
position will stabilize and we achieved the final
clusters (Dênis Martins, 2008).
Figure 8 describes the method used to process
the signals. All biosignals were submitted to a
signal-specific pre-processing phase and then to a
generic signal-independent phase (composed with a
mean wave and clustering procedure) which was
applied to all the signals of this study.
Figure 8: Signal’s processing procedure schematics.
For the pre-processing phase, the acceleration
signals were low-pass filtered using a smoothing
filter with a moving average window of 50 points.
The BVP signal was also low-passed filtered with
the same moving average window as the
acceleration signals. Random noise with 1/5 of
original amplitude was added to the synthetic signal.
The EMG signal was centered at y axis zero, by
subtracting its mean value, and then rectified. Then
we applied the smoothing filter with a moving
average window of 300 points.
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
260

In the next sections the generic processing
procedure will be described.
3.1 Mean wave
The autoMeanwave algorithm is the base function
to identify the individual waves. After running this
algorithm we will have the mean wave computed
with the individual wave’s information.
This algorithm receives, by input, a signal, its
sampling frequency and a trigger mode (this one can
be omitted and the algorithm will use the maximum
point as default).
As we’re working with cyclic signals, the first
step of the automatic mean wave algorithm is the
detection of the signal’s fundamental frequency. For
that we use the fundamentalFrequency
algorithm. With the result we compute the window
size value and randomly selected a part of the signal
with the same number of samples as the window
size. With that signal’s part and the original signal
itself we run sumvolve algorithm to get the signal
events (series of points that we consider the center of
each cycle).
After this we have all the information necessary
to compute the mean wave, which we do in the
computeMeanwave algorithm.
Algorithm 1
autoMeanwave
Input:
Signal, sampling frequency, trigger
mode.
Output:
Fundamental frequency, window size,
events.
Next we will describe minutely the sub-
algorithms referenced above.
Algorithm 2
fundamentalFrequency
Input:
Signal, sampling frequency.
Output:
Fundamental frequency.
In the fundamentalFrequency function,
we smoothed the result of the original signal’s fast
fourier transform with a moving average window of
5% of the signal’s length. We assumed the
frequency value of the first big peak located at the
smoothed FFT signal as the fundamental frequency
of the original signal.
With the fundamental frequency value we could
compute the sampling size of a signal’s cycle. We
call that value “window size”, with a 20% margin:
winsize = (f
S
/ f
0
) *1.2 (1)
Being f
S
the sampling frequency and f
0
the
fundamental frequency. We open the window 20%
to use some more samples than a cycle.
Although there are more robust methods to
determine the fundamental frequency of a signal,
this approach is adequate for our work as the
purpose was to have a close idea of the size of a
cycle. We actually use more than one exact cycle as
we use a margin of 20%, opening the window
calculated with the fundamental frequency. Notice
that further on we use a correlation function to detect
meaningful events on a cycle, so the fundamental
frequency is just used as a preliminary estimation to
support others algorithms.
Algorithm 3
sumvolve
Input:
Two signals
Output:
Distance values.
This algorithm works as a correlation function.
Sliding the smaller window part of the signal (given
by argument) through the original signal, one sample
at a time, this algorithm compares the distance of the
two windows. We used the mean square error as the
distance function:
(2)
The result of this algorithm is a signal composed
with distance values. That distance values shows the
difference between each sliding winsize cycle and
the window selected at the first place.
After, we found all the minimum peaks of the
resulted correlation signal. Those peaks will be our
events.
Algorithm 4
computeMeanwave
Input:
Signal, events, window size.
Output:
Mean wave and standard deviation
error wave.
With the events and the window size, we cut the
signal into periods that we assume as our signal
cycles:
cycle = signal[event – winsize/2 : event
+ winsize/2]
(3)
This way, based on all cycles, we could compute
the mean value to each cycle sample, and compose a
mean wave. The standard deviation error wave is
computed with the same principle, calculating the
standard deviation error instead of the mean value.
For a better visualization of the results, we computed
TWO-MODES CYCLIC BIOSIGNAL CLUSTERING BASED ON TIME SERIES ANALYSIS
261

an error area with the standard deviation error wave
obtained. For that, we added and subtracted one
standard deviation error wave to the mean wave,
getting a superior and inferior wave, to graphically
present the error area (66% of the error). This is
shown in the results section.
After the results shown above, a final adjustment
was made: the alignment of every signal’s cycles.
The position of the mean wave’s minimum point
was detected, and that become our trigger point. The
minimum position was chosen as the trigger position
- we could use the maximum (of the signal or the
derivative), or the zero crossings, for example.
With this trigger point we recalculate the peak
events, or cutting points, used in the
computeMeanwave algorithm:
events = events + trigger – winsize/2 (4)
With the events variable recalculated, we used
the computeMeanWave function again, so the
cycles were aligned and the resultant mean wave
more accurate.
3.2 Clustering
For the clustering procedure we developed a
function that receives the signal to cluster, the
window size and cutting events produced with the
autoMeanwave algorithm.
We go through all the cutting events and for each
we select a part of the signal with center at that event
and a number of samples to both sizes equal to the
window size. Then we compare that cut with each of
the others (with the center in the others cutting
events and the same window size), using the
distance wave-to-wave formula:
Algorithm 5
distanceMatrix
Input:
Signal, Cutting events, window size.
Output:
Matrix with wave-to-wave distances.
(5)
With s
1
and s
2
being the parts of the signal selected
before.
With all of the distance values for each wave, we
built a matrix of distances.
Figure 9: Matrix of distances produced for the synthetic
waves (a)) and the skiing task (b)).
Figure 9 presents two matrixes of distances,
obtained with the imshow command. Figure 9 a)
shows the matrix of the synthetic waves distances
and figure 9 b) the matrix for the skiing task
distances. As we can see, the synthetic matrix is
almost ideal, as all the waves are equal – the
distance values only are minimums or maximums. In
the skiing matrix however, the matrix assumes a
greater variation of distances, as the cycles are not
exactly the same. However, it’s visible the similarity
between the cycles of the same technique (7 cycles
V2, 27 cycles V1 and 8 cycles V2).
To cluster the signal we used the kmeans
algorithm. Those functions received the matrix
created with the distanceMatrix algorithm and
the number of clusters expected in the data, giving
the clusters and distances to the clusters as result.
4 RESULTS AND DISCUSSION
Figure 10 shows the graphics of the resulting mean
waves (line) and deviation error area (filling) after
running the algorithms referenced above. At the left
(figure 10 a.) the graphics represent the initial mean
waves created, before the clustering procedure. At
the right (figure 10 b.) we have the mean waves
representative of the signal parts that were divided
according to the resultant clustering codebook.
It’s visible that the mean waves at the left gather
information about the behavior of the signal, even if
there are some changes in shape or frequency along
the signal. After the clustering procedure there are
some predictable variations in the resultant mean
waves. We notice an overall reduction of the
deviation error after the clustering procedure and
also a reshaping of the mean wave.
After running the clustering procedure we gather
the results for each task performed. These results are
shown in table 1.
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
262

Figure 10: Mean waves of all the tasks before (a)) and after (b)) the clustering procedure.
Table 1: Clustering results.
Task
Number
of Cycles
Cycles
correctly
clustered
Errors Misses
Synthetic 50 49 0 1
Walk and run 343 342 1 0
Run and jump 296 295 1 0
Jumps 85 84 1 0
Skiing 42 41 0 1
Elevation and
squat
23 23 0 0
BVP rest and
afterexercise
165 159 4 2
All 1004 991 7 5
It is important to note that some cycles weren’t
classified, and that occurred because sometimes the
borders of the signal didn’t have a full cycle - the
distanceMatrix algorithm (algorithm 5) cannot
be used to compare a short cycle with the regular
ones. Therefore, those cycles have been rejected for
lack of pattern quality, and won’t be taken into
account.
In the “walk and run” activity there were some
extra classification points. The cycles were correctly
clustered (with only 1 error encountered), but in the
“walking” mode there were some extra points
between those cycles that were also classified. The
reason is a relatively large variation in the
fundamental frequency from the walking to the
running activity - despite one activity has all cycles
well defined (by events variable described at (4)),
the other as less than one cycle per period cut
(because of that change of fundamental frequency).
This condition shows a limitation of our algorithm –
doesn’t allow big changes in the frequency domain
in the different modes presented on the signal.
The errors of classification, note that only 7
errors were encountered, and 2 of those errors were
in transition periods – where the cycle wave is still
TWO-MODES CYCLIC BIOSIGNAL CLUSTERING BASED ON TIME SERIES ANALYSIS
263

reshaping to form the other activity and the distance
value to the mean wave or to the clusters mean
values is bigger than anywhere else on the signal.
This occurred in the jumps and in the walk and run
activities.
Given the results we can affirm that our
clustering algorithm based on the mean wave
information only returned 7 errors out of 999 cycles
with pattern quality, and therefore we achieved
99.2% of efficiency.
5 CONCLUSIONS
The proposed algorithm represents an advance in the
abstract clustering area, as it has an effective
detection of signal variations, tracing different
patterns for distinct clusters, whether it’s an activity,
synthetic or physiological signal.
6 FUTURE WORK
In future work we intend to repeat this procedure to
a wide range of subjects performing the same task,
perform a noise immunity test and also run the
algorithm using a signal with more than two modes.
We intend to introduce an automatically
perception of the cycles which are too distance from
the cluster and assign those cycles to a new
“rejection class”. This will reduce the number of
errors due to a strange cycle, in particular the
mode’s transition cycles.
The local detection of the fundamental frequency
is also a future goal, as we intend to realize when
there’s a major variation of fundamental frequency
and make our algorithms adapt its behavior
according to that variation.
Finally, we have the intention of creating a
multimodal algorithm, which can receive more than
one signal, and process those at the same time and
with the same treatment. This could be useful if we
want to use the 3 axis of an accelerometer, or
conciliate the information of a BVP with an
electrocardiography (ECG) signal.
ACKNOWLEDGEMENTS
The authors would like to thank PLUX – Wireless
Biosignals for providing the acquisition system and
sensors necessary to this investigation. We also like
to thank NIH, the Norwegian School of Sports and
Science, Håvard Myklebust and Jostein Hallén for
acquiring and allowing us to work with the Skiing
signal used in this study. We acknowledge Rui
Martins and José Medeiros for their help and advices
on the BVP acquisition procedure.
REFERENCES
Andersson, E., Supej, M., Sandbakk, Ø., Sperlich, B.,
Stöggl, T., Holmberg, H. (2010) Analysis of sprint
cross-country skiing using a differential global
navigation satellite system. Eur J Appl Physiol. DOI
10.1007/s00421-010-1535-2
Baek, J., Lee G., Park, W., Yun, B. (2004). Accelerometer
Signal Processing for User Activity Detection,
Knowledge-Based Intelligent Information &
Engineering Systems, Vol. 3215/2004, 610-617. DOI
10.1007/978-3-540-30134-9_82
Ben-Arie, J., Wang, Z., Pandit, P., Rajaram, S. (2002).
Human Activity Recognition Using Multidimensional
Indexing. IEEE Transactions on Pattern Analysis and
Machine Intelligence, vol. 24, no. 8, 1091-1104.
Fridlund, A., Schwartz, G., Fowler, S. (2007) Pattern
Recognition of Self-Reported Emotional State from
Multiple-Site Facial EMG Activity During Affective
Imagery. Society for Psychophysiological Research.,
vol. 21, no. 6. DOI 10.1111/j.1469-
8986.1984.tb00249.x
Liao, T. Warren. (2005) Clustering of time series data – a
survey. Pattern Recognition 38 (2005) 1857 – 1874.
Martins, D., Mattos, M., Simões, P., Cechinel, C., Bettiol,
J.; Barbosa, A. (2008) Aplicação do Algoritmo K-
Means em Dados de Prevalência da Asma e Rinite em
Escolares. In: XI Congresso Brasileiro de Informática
em Saúde (CBIS'2008), 2008.
PLUX – Wireless Biosignals, bioPLUX Research Manual,
PLUX’s internal report, 2010.
Quiroga, Rodrigo Q. (2007) Spike sorting. Scholarpedia,
2(12):3583
Smith, J., Fishkin, K., Jiang, B., Mamishev, A., Philipose,
M., Rea, A., Roy, S., Sundara-Rajan, K. (2005).
RFID-Based Techniques for Human-Activity
Detection. Communications of the ACM, vol. 48, no.
9, 39-44.
T. Oliphant. Guide to Numpy. Tregol Publishing, 2006.
T. Oliphant. SciPy Tutorial. SciPy, http://www.scipy.org/
SciPy Tutorial, 2007.
Wu, X., Kumar, V., Quinlan J., Ghosh J., Yang, Q.,
Motoda, H., McLachlan, G., Ng, A., Liu, B., Yu, P.,
Zhou, Z., Steinbach, M., Hand, D., Steinberg, D.
(2007). Top 10 algorithms in data mining. Knowledge
Information Systems, 14:1–37. DOI 10.1007/s10115-
007-0114-2
www.opensignals.net, last accessed on 15/07/2010
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
264
