TOWARDS FAST 3D NANOPARTICLE LOCALIZATION

FOR STUDYING MOLECULAR DYNAMICS IN LIVING CELLS

Stefan Sokoll

1,2

, Klaus T¨onnies

and Martin Heine

Research Group Molecular Physiology, Leibniz Institute for Neurobiology, Magdeburg, Germany

Research Group Computer Vision, Otto-von-Guericke University, Magdeburg, Germany

Keywords:

3D particle localization, Nanometer sub-resolution, Live cell imaging, Confocal ﬂuorescence microscopy.

Abstract:

Studying molecular dynamics is crucial for understanding biological processes in living cells. In principle, this

is achieved by attaching ﬂuorescent particles to molecules of interest and their detection using ﬂuorescence

microscopy. These analysis require fast optical techniques with at least 20Hz frame rate and a resolution

below the diffraction limit in all three spatial dimensions. Current approaches basically rely on determining

the correlation between features of the particle’s 2D point spread function (PSF) and the focal distance to the

center of the particle. However, they are still unsuitable for the application to live cell imaging where the

refractive index mismatch is present. This mismatch leads to non-stationary optical properties of the particles

on which the algorithms rely, necessitating a calibration procedure prior to every experiment. However, this is

almost unfeasible to particles attached to living cells.

We established a spinning disk confocal setup and employ Quantum dots (QD) as ﬂuorescence particles. Cor-

responding models of the axial PSF features that deﬁne the distance to the center of the particle are developed

and analyzed in the presence of the refractive index mismatch. We present this analysis as the base for the

future development of a 3D localization technique applicable to living cells.

1 INTRODUCTION

Neurons are polarized cells that communicate via

synapses with each other. Each synapse consists of a

pre- and post-synaptic side, with the ﬂow of informa-

tion going from the former to the latter. Basically, on

the arrival of a signaling action potential at a chem-

ical synapse, the interplay of different molecules at

the pre-synapse may lead to a release of neurotrans-

mitters into the synaptic cleft (see Figure 1). After ab-

sorbance by receptors at the post-synaptic side, neu-

rotransmitters may be again convertedinto a signaling

potential.

Figure 1: Signal transmission at a chemical synapse.

The probability of successful signal transmission

between the pre- and post-synaptic side is liable to

strong variation, which is called synaptic plasticity. It

is believed to be fundamental for learning and mem-

ory. Many different molecules participate in synaptic

transmission, e.g. adhesion molecules, receptors, and

voltage-gated ion channels. In order to be successful,

their arrangement, number, and density seems to be

very important. In particular, molecular dynamics at

the active zone of the pre-synapse, which describes

the area of possible neurotransmitter release, are of

special interest.

A well established technique for studying molec-

ular dynamics in living cells is the attachment of ﬂu-

orescent particles at molecules of interest and their

detection using ﬂuorescence microscopy. This pro-

cedure involves the acquisition of time-series images,

either solely two-dimensional or taken at different fo-

cal positions combined to three-dimensional stacks.

The trajectories of single particles are then computed

from the particular position in each acquisition (see

Figure 2).

Studying molecular dynamics requires the optical

techniques to perform with at least 20Hz frame rate

210

Sokoll S., Tönnies K. and Heine M..

TOWARDS FAST 3D NANOPARTICLE LOCALIZATION FOR STUDYING MOLECULAR DYNAMICS IN LIVING CELLS.

DOI: 10.5220/0003166502100215

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2011), pages 210-215

ISBN: 978-989-8425-36-2

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 2: Microscopic 3D image of a QD (in red) and its

preceding trajectory (in blue), together with synapses (in

green), allowing colocalization analysis.

and a resolution at the molecular level in all three

spatial dimensions. For biological applications, 20Hz

frame rate are necessary to distinguish different types

of molecular diffusion by their diffusion coefﬁcients.

High spatial resolution in all three dimensions is es-

pecially required as the active zone is usually not big-

ger than 100-500nm in size and does not necessar-

ily reside in plane with the focal plane of the micro-

scope. To date, various approaches have been devel-

oped, but these techniques are only suitable in the ab-

sence of the refractive index mismatch, which is the

deviation of the refractive indices between the objec-

tive’s immersion medium and the observed biologi-

cal medium. As this mismatch is unavoidable in live

cell imaging, the optical properties of the particles on

which the algorithms rely, cannot be expected to be

stationary along the optical axis (Hell et al., 1993).

Thus, a calibration has to be performed prior to every

experiment, which is almost unfeasible to particles at-

tached to living cells and remains a major challenge.

In this paper, we present a model for the optical

properties of Quantum dot (QD) nanoparticles, im-

aged with a spinning disk confocal setup, and analyze

it in the presence of the refractive index mismatch.

We ﬁrst highlight recent developments in the ﬁeld of

single nanoparticle localization followed by the pre-

sentation of our axial model. Furthermore, we ana-

lyze the model qualitatively and ﬁnally conclude that

the inﬂuence of the refractive index mismatch has to

be considered.

2 RELATED WORK

In confocal ﬂuorescence microscopy, the spatial reso-

lution is limited to 200-300nm in the lateral and about

500-700nm in the axial direction by the diffraction of

light (Huang et al., 2009). Thus, the image of every

sharp spot on the object appears with a blurred inten-

sity proﬁle in the image plane of the microscope. This

is referred to as the point spread function (PSF) of the

microscope and deﬁnes the minimal distance of two

light sources such that they can still be resolved in the

image.

Localization microscopyis a reasonabletechnique

to overcome this limitation ((Schmidt et al., 1996),

(Kubitscheck et al., 2000), (Cheezum et al., 2001)).

For two-dimensional images, this technique basically

comprises the ﬁtting of a Gaussian functionto the PSF

of a particle (see Figure 3). Thus, at least the center

Figure 3: Principle of localization microscopy, leading to

sub-pixel localization accuracy.

of a particle can be determined with higher accuracy

than the resolution, leading to an accuracy δx approx-

imated by

δx =

√

, (1)

where s is the standard deviation of the PSF and N the

number of collected photons (Thompson et al., 2002).

By analyzing image stacks, this technique is in

principle extendable to 3D. The axial center of the

particle is deﬁned by the minimum standard devia-

tion of the Gaussian ﬁts in all slices ((van Oijen et al.,

1998), (Sch¨utz et al., 2000), (Ragan et al., 2006)).

However, such approaches show only a poor time res-

olution due to the necessity to acquire multiple im-

ages for one stack, leading to deformations of the PSF

induced by particle movement (see Figure 4). Re-

Figure 4: (a) shows the symmetric 3D PSF of an immobile

particle. Due to particle movement, the PSF shown in (b) is

deformed.

TOWARDS FAST 3D NANOPARTICLE LOCALIZATION FOR STUDYING MOLECULAR DYNAMICS IN LIVING

CELLS

211

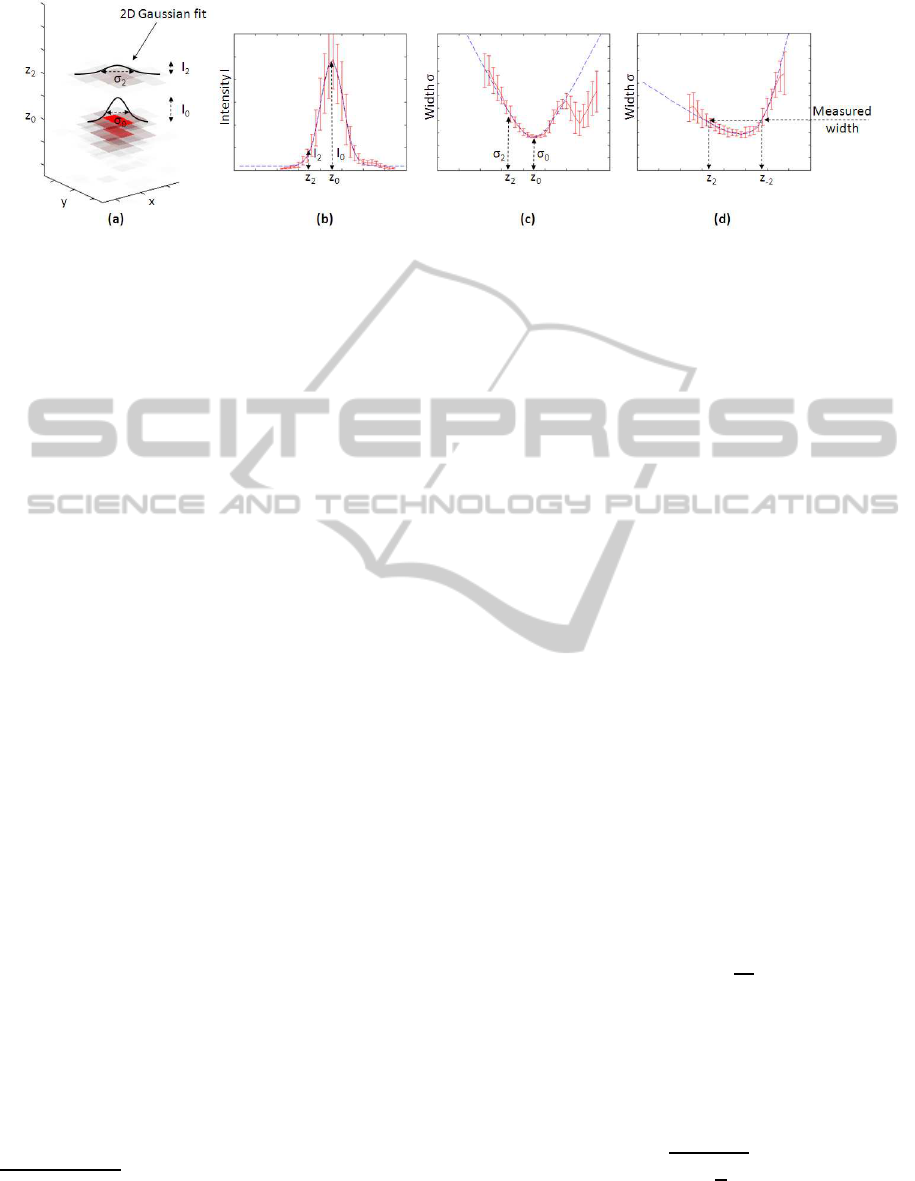
Figure 5: Axial dependency of 2D PSF features. (a) Illustrates the computation of the 2D PSF features of a 3D particle. The

resulting approximations to the Gaussian intensity and the parabolic width curve are presented in (b) and (c), respectively. The

measurements, together with the standard deviations, are shown in red and the approximations to the measurements in blue.

The parabola becomes asymmetric (d), if the refractive indexes differ. Knowing the particular curve, allows the computation

of the ambiguous distance to the center of the particle from a single measurement.

cently developed techniques allow the computation of

the axial position from one image slice by defocusing

the image ((Speidel et al., 2003), (Wu et al., 2005)) or

introducing an astigmatism into the light path ((Kao

and Verkman, 1994), (Holtzer et al., 2007)). The ba-

sic principle amounts to determine the correlation be-

tween features of the 2D PSF and the focal distance to

the center of the particle. However, due to the refrac-

tive index mismatch this correlation varies with the

depth of the particle within the biological medium and

needs to be adjusted for each experiment. This makes

current algorithms unsuitable for live cell imaging as

particles attached to molecules of living cells cannot

be immobilized for calibration.

3 AXIAL MODEL

The presented techniques were mostly carried out on

wideﬁeld microscopes. We established a spinning

disk confocal setup

, to combine the advantages of

improved spatial resolution as well as the ability to

image particles that reside deeper within the medium

(Inou´e, 2006). Decreased signal intensity is the down-

side of this choice, leading to less accurate localiza-

tion results (see Equation 1). However, in the fu-

ture, this tradeoff allows us to apply the technique

to thicker brain slices, which are biologically more

relevant than primary cultured neurons. As ﬂuores-

cence particles, we use QDs, which are semiconduc-

tor nanoparticles exhibiting excellent photostability

and narrow emission spectra (Toomre and Pawley,

2006).

Initially, we analyzed axial scans of QDs that were

In detail, our setup comprises a Nano Focusing

Piezo Stage (PRIOR Scientiﬁc), an Olympus Microscope

(BX51WI), a Yokogawa spinning disk (CSU-X1), and an

Andor iXionEM+897 CCD camera.

immobilized below the cover slip such that the refrac-

tive index mismatch had no inﬂuence. Here we found

two features of the PSF that vary with the axial dis-

tance of the measurement to the center of the particle.

These are the intensity I and the width σ of the ﬂuo-

rescent peaks at each axial position (see Figure 5(a)).

They are computed from the height and the full width

at half maximum (FWHM) of the Gaussian ﬁts, re-

spectively. As it is depicted in Figures 5(b-c), the

axial intensity distribution follows a Gaussian func-

tion and the width of the ﬂuorescence peaks matches

a parabola.

Considering the refractive index mismatch by im-

mobilizing QDs at different depths below the cover

slip, the parabola of the width becomes asymmet-

ric, where the asymmetry correlates with the depth

of the particle within the observed medium (see Fig-

ure 5(d)). The Gaussian function of the intensity is

also slightly skewed for higher particle depths. How-

ever, we found the differences to be neglectable and

for simplicity of the model, we retain a symmetric in-

tensity distribution at the moment.

Based on our experimental observations, we iden-

tiﬁed approximations to both curves. The correlation

of the intensity is modeled as a Gaussian function

given by

I(z) = o + h·e

−

, (2)

where o, h and c are the offset, height and standard

deviation, respectively. The axial dependency of the

PSF’s width is described in (Niedrig, 1993) and ex-

tending the presented formula to consider the asym-

metry introduced by the refractive index mismatch,

we get

σ(z) = σ





+ m·z, (3)

where d is the focal depth, σ

the FWHM in focus and

m represents the skewness of the parabola. Solving

BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms

212

Figure 6: (a-c) Present the axial localization accuracy dis-

tribution, the correctness of the axial model and the axial

dependency of the lateral position, respectively. All graphs

belong to measurements at 5µm depth. (a) and (c) show

measurements of individual particles and (b) provides the

average result of all particles at this depth. Illustrative ex-

amples that explain how the given curves are computed are

presented next to each graph.

these equations for z, we can compute the axial posi-

tion of the particle from only one slice applying either

the Gaussian or the parabolic approximation to the in-

tensity or the width, respectively. However, so far the

model cannot distinguish if the particle is above or

below the focal plane, as it is depicted in Figure 5(d).

4 QUALITATIVE ANALYSIS OF

THE MODEL

After introduction of the axial model we now provide

further properties that have to be considered for the

development of a fast 3D localization algorithm. We

present only qualitative results because the ﬁnal accu-

racy of the localization depends mainly on the imag-

ing conditions

First, we have analyzed the dependency of the ax-

ial localization accuracy on the distance of the im-

age acquisition to the center of the particle (see Fig-

ure 6(a)). It becomes apparent that the accuracy dis-

tributions of the intensity I and the width σ proceed

contrary to each other. The intensity model provides

higher accuracy when the particle is off-focus while

the width model has best accuracy close to the center

position. The shape of these accuracy distributions

is typical for all depths, but the localization accuracy

worsens with increasing depth. However, the contrary

course of the distributions supports the development

of a fusion strategy, possibly leading to a constant lo-

calization accuracy valid at all axial scan positions.

Next to the axial localization accuracy, the cor-

rectness of the approximation to the PSF has to be

determined. Figure 6(b) shows the systematic errors

of the axial model, computed from the constant devi-

ation of the model to the mean measurements at each

axial scan position. It reveals that the measured data

twists around the approximation, which is valid for

all depths and is consistent with earlier ﬁndings from

(Sch¨utz et al., 2000). Of course, in principle a more

accurate PSF could be computed, however, the cor-

rect computation requires the knowledge about opti-

cal properties of the setup that are generally not acces-

sible as (Speidel et al., 2003) already pointed out. We

consider a more accurate model as a possible future

improvement to the accuracy of the localization algo-

rithm. For now we accept that error, which is only

in the order of 1/4 of the localization accuracy and

is expected to be reducible via fusion of the models.

Furthermore, we found the systematic error to remain

constant for all tested depths.

To compute the 3D position of a particle, the de-

pendencyof the lateral position on the axial scan posi-

tion is also required. Figure 6(c) shows that the lateral

position varies with different measurements along the

axial axis. This hinders the computation of the lat-

eral position independently of the axial position and

has to be further investigated. However, at least these

curve shapes, presented in Figure 6(c), are generally

valid for all particles and depths. Finally, we found

that the lateral localization accuracy is best at the cen-

ter of the particle, which agrees with Equation 1 and

slightly improves with increasing depth.

Current data was acquired by imaging of QDs emitting

655nm light with an oil objective of magniﬁcation 100x.

QDs were illuminated by 488nm light and consecutively

scanned for 50ms with z-stacks covering 4µm and a step

size of 100nm. 50 z-stacks were acquired of each particle.

TOWARDS FAST 3D NANOPARTICLE LOCALIZATION FOR STUDYING MOLECULAR DYNAMICS IN LIVING

CELLS

213

Figure 7: Variation of axial model parameterization for particles at different depths. (b) shows width curve examples for each

depth with the measured data in red and the parabolic approximations in a dedicated color. (a) and (c) visualize the PSF for

particles at depth 0µm and 15µm, respectively.

5 INFLUENCE OF THE

REFRACTIVE INDEX

MISMATCH

The presented axial model considers the refractive in-

dex mismatch and is valid independently of the par-

ticle’s depth in the medium. However, the parame-

ters of the model change with varying depths in the

medium.

To prove that the consideration of this variation

is necessary, we performed calibration measurements

at different depths with QDs immobilized in Mowiol

and at monolayers of HEK cells

. The test set com-

prises always 40 particles at depths of 0, 5, 10 and

15µm in Mowiol and at 0 and 5µm at HEK cells. Each

particle was axially scanned 50 times. Figure 7 de-

picts example data from width measurements at dif-

ferent depths in Mowiol. The different depths are

color coded. It becomes apparent that the curve is

symmetric only at zero depth and turns asymmetric

for higher depths.

Analysis of the curve parameters revealed that the

standard deviation c of the Gaussian and the gradient

m of the parabola increase with depth. They uniquely

deﬁne a certain depth. Figure 8 depicts the different

curves when only these classifying parameters are ad-

justed to the depth and mean values are taken for the

remaining ones.

Using wrong parameters for the model will lead

to the computation of incorrect axial positions of the

particle. For instance, let’s assume that a particle was

acquired at depth 5µm but is mistakenly expected to

be at depth 10µm. Given that, Figure 9 shows the

axial position error for each slice in the stack. It is

apparent that in this example the error is roughly half

as large as the axial localization accuracy presented in

Mowiol is a transparent embedding medium for cell

preparations. HEK cells are Human Embryonic Kidney

cells, widely used in cell biology research due to their sim-

ple handling and fast growth.

Figure 8: The mean intensity and width curves at different

particle depths if only the Gaussian standard deviation c,

respectively the gradient m, are adjusted. These ﬁndings

are valid for Mowiol and HEK cell preparations.

Figure 6(a) even though only the classifying parame-

ters are varied. Hence, the error cannot be neglected

and this proves that for live cell imaging, where the re-

fractive index mismatch cannot be avoided, calibrat-

ing the model parameters is indispensable.

Figure 9: Illustrated are the axial position errors for each

model in case one mistakenly expects a particle at depth

10µm instead of its correct position at 5µm.

6 CONCLUSIONS

We presented a model that facilitates the fast 3D local-

ization of nanoparticles in living cells, using a spin-

ning disk confocal setup. We performed qualitative

analyzes and described its dependency on the parti-

cle’s depth in the medium, proving that the refrac-

tive index mismatch has to be considered for live cell

imaging applications.

We propose two major objectives for future work.

BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms

214

First, we have to develop a localization algorithm

that takes the properties of our model into account.

Here, major challenges are the ambiguity of the axial

model, which we like to address by the introduction

of a cylindric lens in the light path as well as a fusion

strategy for the intensity and width models to increase

the localization accuracy. Second, and far more im-

portant, we have to solve the problem that the model

parameters cannot be adjusted via calibration. Here,

we focus on the estimation of the parameters during

each experiment by formulation as an expectation-

maximization problem.

ACKNOWLEDGEMENTS

This work is supported by grants from the DFG (HE

3604/2-1).

REFERENCES

Cheezum, M. K., Walker, W. F., and Guilford, W. H. (2001).

Quantitative comparison of algorithms for tracking

single ﬂuorescent particles. Biophysical Journal,

81:2378–2388.

Hell, S., Reiner, G., Cremer, C., and Stelzer, E. H. K.

(1993). Aberrations in confocal ﬂuorescence mi-

croscopy induced by mismatches in refractive index.

Journal of Microscopy, 169:341–405.

Holtzer, L., Meckel, T., and Schmidt, T. (2007). Nanometric

three-dimensional tracking of individual quantum dots

in cells. Applied Physics Letters, 90.

Huang, B., Bates, M., and Zhuang, X. (2009). Super-

resolution ﬂuorescence microscopy. Annual Review

of Biochemistry, pages 993–1016.

Inou´e, S. (2006). Foundations of confocal scanned imaging

in light microscopy. Handbook of Biological Confocal

Microscopy, pages 1–16.

Kao, H. P. and Verkman, A. S. (1994). Tracking of single

ﬂuorescent particles in three dimensions: use of cylin-

drical optics to encode particle position. Biophysical

Journal, 67:1291–1300.

Kubitscheck, U., K¨uckmanna, O., Kuesa, T., and Peters, R.

(2000). Imaging and tracking of single gfp molecules

in solution. Biophysical Journal, 78:2170–2179.

Niedrig, H. (1993). Lehrbuch der Experimentalphysik. Wal-

ter de Gruyter, Berlin, 9th edition.

Ragan, T., Huang, H., So, P., and Gratton, E. (2006). 3d

particle tracking on a two-photon microscope. Journal

of Fluorescence, 16:325–336.

Schmidt, T., Sch¨utz, G. J., Baumgartner, W., Gruber, H. J.,

and Schindler, H. (1996). Imaging of single molecule

diffusion. Proceedings of the National Academy of

Sciences of the United States of America, 93:2926–

2929.

Sch¨utz, G. J., Pastushenko, V. P., Gruber, H. J., Knaus,

H. G., Pragl, B., and Schindler, H. (2000). 3d imag-

ing of individual ion channels in live cells at 40 nm

resolution. Single Molecules, 1:25–31.

Speidel, M., Jon`a˘s, A., and Florin, E. L. (2003). Three-

dimensional tracking of ﬂuorescent nanoparticles with

subnanometer precision by use of off-focus imaging.

Optics Letters, 28:69–71.

Thompson, R. E., Larson, D. R., and Webb, W. W. (2002).

Precise nanometer localization analysis for individual

ﬂuorescent probes. Biophysical Journal, 82:2775–

2783.

Toomre, D. and Pawley, J. B. (2006). Disk-scanning con-

focal microscopy. Handbook of Biological Confocal

Microscopy, pages 221–237.

van Oijen, A. M., K¨ohler, J., Schmidt, J., M¨uller, M.,

and Brakenhoff, G. J. (1998). 3-dimensional super-

resolution by spectrally selective imaging. Chemical

Physics Letters, 292:183–187.

Wu, M., Roberts, J. W., and Buckley, M. (2005). Three-

dimensional ﬂuorescent particle tracking at micron-

scale using a single camera. Experiments in Fluids,

38:461–465.

TOWARDS FAST 3D NANOPARTICLE LOCALIZATION FOR STUDYING MOLECULAR DYNAMICS IN LIVING

CELLS

215