OPTICAL METHODS FOR LOCAL PULSE WAVE

VELOCITY ASSESSMENT

T. Pereira, M. Cabeleira, P. Matos, E. Borges, V. Almeida, J. Cardoso, C. Correia

Instrumentation Center, Physics Department, University of Coimbra, R Larga, Coimbra, Portugal

H. C. Pereira

Instrumentation Center, Physics Department, University of Coimbra, Coimbra, Portugal

ISA- Intelligent Sensing Anywhere, Coimbra, Portugal

Keywords: Optical probes, Photodiode, Waveform distension, Pulse Transit Time, Pulse Wave Velocity.

Abstract: Pulse wave velocity (PWV) is a clinically interesting parameter associated to cardiac risk due to arterial

stiffness, generally evaluated by the time that the pressure wave spends to travel between two arbitrary

points. Optic sensors are an attractive instrumental solution in this kind of time assessment applications due

to their truly non-contact operation capability, which ensures an interference free measurement. On the

other hand, they can pose different challenges to the designer, mostly related to the features of the signals

they produce and to the associated signal processing burden required to extract error free, reliable

information. In this work we evaluate two prototype optical probes dedicated to pulse transit time (PTT)

evaluation as well as three algorithms for its assessment. Although the tests were carried out at the test

bench, where “well behaved” signals can be obtained, the transition to a probe for use in humans is also

considered. Results demonstrated the possibility of measuring pulse transit times as short as 1 ms with less

than 1% error.

1 INTRODUCTION

Pulse wave velocity (PWV) is defined as the

velocity at which the pressure waves, generated by

the systolic contraction of the heart, propagate along

the arterial tree. PWV is a measure of regional

arterial stiffness of the arterial territory between the

two measurement sites. This parameter is related to

the elastic modulus (E) of the arterial wall (which

represents the intrinsic wall stiffness), and the

arterial geometry (thickness: h) and blood density

(ρ). The first relationship was formulated by Moens

and Korteweg and expresses:

PWV =

(1)

Later on, Bramwell and Hill described (1) the

association in terms of distensibility (D), which is

determined by the blood vessel’s compliance (C),

the former relation can be expressed:

PWV

(2)

From the expression, we can deduce that higher

PWV corresponds to lower vessel distensibility and

compliance and therefore to higher arterial stiffness.

The pulse waves travel through the arteries at a

speed of 4 to 10 meters per second depending on the

vessel (PWV increases with the distance from the

heart), and the elastic condition of the arterial wall,

which is affected by a variety of factors in health

and disease (Bramwell, 1922; Nichols, 2005).

The most common technique to assess non-

invasively PWV is based on the acquisition of pulse

waves generated by the systolic ejection at two

distinct locations, separated by a distance d, and

determination the time delay, or pulse transit time,

due to the pulse wave propagation along the arterial

tree (Rajzer, 2008). The PWV parameter is then

simply calculated as the linear ratio between d and

the PTT.

Pereira T., Cabeleira M., Matos P., Borges E., Almeida V., Cardoso J., Correia C. and C. Pereira H..

OPTICAL METHODS FOR LOCAL PULSE WAVE VELOCITY ASSESSMENT.

DOI: 10.5220/0003166800740081

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2011), pages 74-81

ISBN: 978-989-8425-35-5

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

Many different pulse waves have been used to

assess pulse wave velocity, such as pressure wave,

distension wave or flow wave. The gold standard in

PWV assessment uses pressure waves measured by

pressure sensors (Laurent, 2006). These sensors

need to exert pressure in the blood vessel this will

distort the waveform, and may lead to inaccurate

measurements. Another drawback of this method is

the fact that the predicted PWV is relative to a large

extension of the arterial tree and therefore is the

conjunction of different local PWVs.

Other studies describe ultrasonic probes that

predict PWV using Doppler Effect and modified

ecography probes (Minnan Xu, 2002), but the PWV

measurements were unreliable.

Recently (Kips et al, 2010; Vermeersch et al,

2008), described alternative approaches for

estimating carotid artery pressures with an

ultrasound system. Calibrated diameter distension

waveforms were compared to the more common

approach based on pressure waves, proving to be a

valid alternative to local pressure assessment at the

carotid artery.

All the previous techniques are minimally

invasive, but the probe has to be in contact with the

patient’s tissues at the artery site. This contact, as

stated above, can distort the signal integrity and thus

rise the interest in exploring true non-contact

technique.

The propagation of pressure waves in arterial

vessels generates distensions in the vessel’s walls.

These distensions can be optically measured in

peripheral arteries like the carotid that, as they run

very close to the surface impart a visible distention.

This distention, as it modulates the reflection

characteristics of the skin, can be used to generating

an optical signal correlated with the passing pressure

wave.

The probes developed in this work, gather the

light generated by LED illumination and reflected by

the skin, using two photodiodes placed 3 cm apart,

all assemble in a single probe. PWV is assessed by

measuring the time delay between the signals of the

two photo-sensors using different algorithms that are

also discussed.

2 TECNOLOGIES

Two distinct types of silicon optical sensors – planar

and avalanche photodiode (APD) – are used in this

work, each one requiring a particular electronic

circuitry. Results, however, are derived by the same

signal processing algorithms.

Each probe incorporates two identical optical

sensors placed 3 cm apart and signal conditioning

electronics based on a transconductance amplifier

and low-pass filter. The APD probe includes the

high voltage biasing circuitry (250V) necessary to

guarantee the avalanche effect. Illumination is

provided by local, high brightness, 635 nm light-

emitting diodes (LEDs).

A photodiode (PD) is a type of photo-detector

with the ability of converting light into either current

or voltage, according to the modus operandi. One

decided to use a planar, rectangular-shaped

photodiode, its dimensions being 10.2x5.1mm. This

is silicon solderable photodiode feature low cost,

high reliability and a linear short circuit current over

a wide range of illumination.

Analogously to the conventional photodiodes,

APDs operate from the electron-hole pairs created

by the absorption of incident photons. The high

reverse bias voltage of APDs, however, originates a

strong internal electric field, which accelerates the

electrons through the silicon crystal lattice and

produces secondary electrons by impact ionization.

This avalanche effect is responsible for a gain factor

up to several hundred.

APDs are operated with a relatively high reverse

voltage and will typically require 200 to 300 volts of

reverse bias. Under these conditions, gains of around

50 will result from the avalanche effect, providing a

larger signal from small variations of light reflected

from the skin and will, at least theoretically, improve

the signal-to-noise ratio (SNR).

On the other hand, since the sensitive area of this

sensor is very small (1 mm

), the accuracy of the

estimations increases. In fact, comparatively to the

planar photodiode, in which the detection of light

takes place over a much larger area, this sensor can

measure an almost punctual section of the skin, thus

decreasing the error associated to the detection solid

angle.

The two prototype probes, on which we support

this work, incorporate an APD from Adavanced

Photonics (SD 012-70-62-541) and a planar type

from Silonex (SLCD-61N3) respectively.

3 TEST SETUP

The test setup was designed to assess the two main

parameters of in PWV measurements: linearity and

time resolution.

Their assessment was carried out in a test setup

where illumination is provided by two LEDs whose

light intensities reproduce the same signal with a

OPTICAL METHODS FOR LOCAL PULSE WAVE VELOCITY ASSESSMENT

variable time delay between them, as shown in

Figure 1.

Two arbitrary waveform generators, Agilent

33220A (AWG1 and AWG2), are synchronously

triggered by an external signal. The waveform

generators have been previously loaded with the

same typical cardiac waveforms and the mutual

delay is selected in order to simulate different pulse

transit times (Figure 2). These signals must be added

to a small offset of the order of the magnitude of the

forward voltage drop of the LED, so that the

resulting light intensity is linearly modulated by the

LED signal current. A 16-bit resolution data

acquisition system (National Instruments, USB6210)

samples the signals at a 20 kHz rate, adequate for

PTTs as low as 100 µs and stores them for off-line

analysis using MatlabTM.

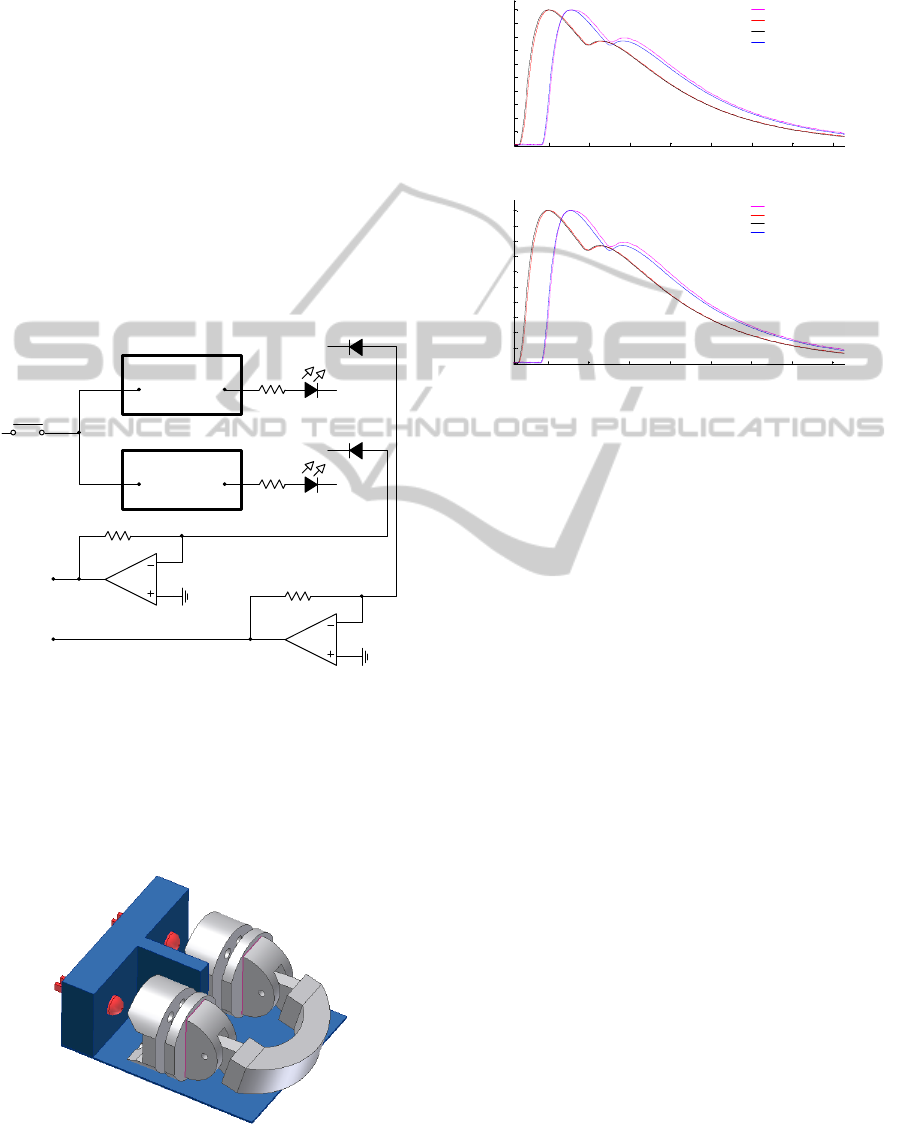
Figure 1: Light modulation and detection circuit.

In the test setup, the probe is placed in front of a

test device, see Figure 2, which holds the two

modulated LEDs and provides light isolation to

prevent crosstalk. During the tests, the LEDs of the

probe itself are deactivated and all light comes from

the LEDs in the test device.

Figure 2: During test, the probe is held to the blue part.

The test LEDs activated by circuit of Figure 1.

Figure 3 shows a typical set of signals generated and

detected by the circuit of Figure 1.

Figure 3: Excitation and detector responses for a) Planar

Photodiode b) Avalanche Photodiode.

To assess the operational limits of our probes and

algorithms, we designed three different tests. In the

first one, signals with frequency similar to the

normal heart rate but with delays within the

interesting PTT range are fed to the system to

investigate the integral linearity error. This test was

performed at a constant frequency of 1.5 Hz and

time delays varying from 1ms to 100ms,

corresponding to PWVs in a 30m/s to 0.3m/s

interval. This range of values includes the normal

PTT range of values in humans.

In the second test we assess the robustness of the

algorithms to noise. To do this, we add white noise

of amplitudes ranging from 1% to 50% of the signal

amplitude in 0.02% steps, to the isolated pair of

pulses. For each noise level, 1000 samples produced

in order to obtain reasonable statistics. The resulting

PTT distribution is then studied.

The third test was intended to validate our

algorithm’s operability under a wide range of

frequencies (simulating different Heart rates) with a

time lag far greater than the maximum PTT seen in

humans. It consisted of varying the output frequency

(1 Hz to 200 Hz) of the cardiac pulses keeping the

time lag between the two signals at 1.1ms.

Trigger

PD1

PD2

AWG1

AWG2

0.05 0.1 0.15 0.2 0.25 0. 3 0. 35 0.4

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Time [sec]

Amplitude [A.U.]

Signal Sensor 1

Signal Sensor2

Signal LED 1

Signal LED 2

0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Time [sec]

Amplitude [A.U.]

Signal Sensor 1

Signal Sensor2

Signal LED 1

Signal LED 2

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

4 SIGNAL PROCESSING

Three different algorithms for extracting the time

delay from the detector’s signals are considered.

They are referred to as foot-to-foot, cross-correlation

and phase spectra. Their basis derives from the

homonymous mathematical functions.

The accuracy of the results delivered by the

algorithms discussed in this section is compared

with the reference delay selected at the waveform

generators.

In the foot-to-foot method and in spite of more

complex methods (Kazanavicius, 2005), a simple

detection of the time lag between the start of the

upstroke of the two consecutive pulses is carried out.

This is possible due to the well behaved nature and

low noise levels of our signals. A different situation

occurs in signals collected from a patient, mostly

due to baseline drift.

The cross-correlation method is based on the

well known property of the peak of cross-

correlogram that allows delays to be calculated by

subtracting the peak time position from the pulse

length (Azaria, 1984). Two different correlation

functions are used: one that belongs to the

MatlabTM core (Xcorr) and another one that

generates the cross-correlation making direct use of

the cross-correlation theorem (Fcorr).

The third method uses data in the phase spectra

of the signals. In this method, we first identify the

exact frequency of the signal’s harmonics, using the

amplitude spectra, and then, extract the

corresponding phase angles from the phase spectra.

The phase angle, θ, is related with angular

frequency of the phase spectrum, ω and with the

time delay, t, according to:

t⋅=

(3)

On its turn, the time delay is computed from the

phase angles of the same harmonic in the phase

spectra of each signal, θ

and θ

(

)

−

(4)

Despite the fact that, theoretically, the time delay

can be determined at any harmonic of the complete

spectrum, the practice, however, differs, given their

affectation by noise. Nevertheless, by performing

the filtering at the detector amplifier level, one is

able to obtain a lower error, as long as the best

harmonics (that is, with the highest SNR possible)

are selected. For the circuits used in this study, one

checked best performances when the time delay was

computed at the 2nd harmonic in the APD case and

in the 4th one for the PP circuits.

5 RESULTS

This section is dedicated to the discussion of results

obtained with the two probes using the previously

mentioned algorithms.

5.1 Integral Linearity

By definition, integral linearity is the maximum

deviation of the results from the reference straight

line, expressed as a percentage of the maximum. We

explore delays in the 1 to 100 ms interval. Results

are shown in Figures 4 and 5.

A higher number of points are taken close to the

origin since this is the interesting range of values in

human PTT studies using the optical probes.

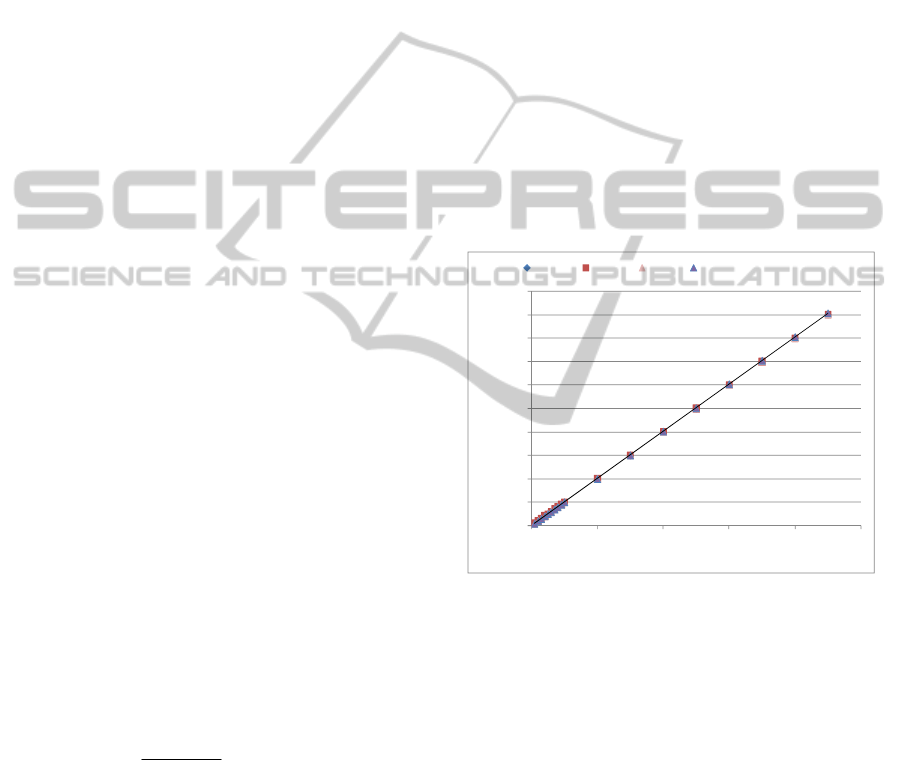
Figure 4: Reference Delay versus measured delay for the

PP probe. The APD curve practically coincides with this

one.

For both probes, all the algorithms produce highly

linear (better than 1%) results as well as low error

agreement with the reference time delay.

5.2 PTT Error

Error plots, expressed as a percentage of the

corresponding reference value, are shown in Figures

5 and 6. We discuss the main differences between

the PP and the APD probes.

y = 1,0067x -0,0002

R² = 1

0,01

0,02

0,03

0,04

0,05

0,06

0,07

0,08

0,09

0,1

0 0,02 0,04 0,06 0,08 0,1

Time Delay [sec]

Reference Time Delay [sec]

Xcorr Fcorr Foot Phase

OPTICAL METHODS FOR LOCAL PULSE WAVE VELOCITY ASSESSMENT

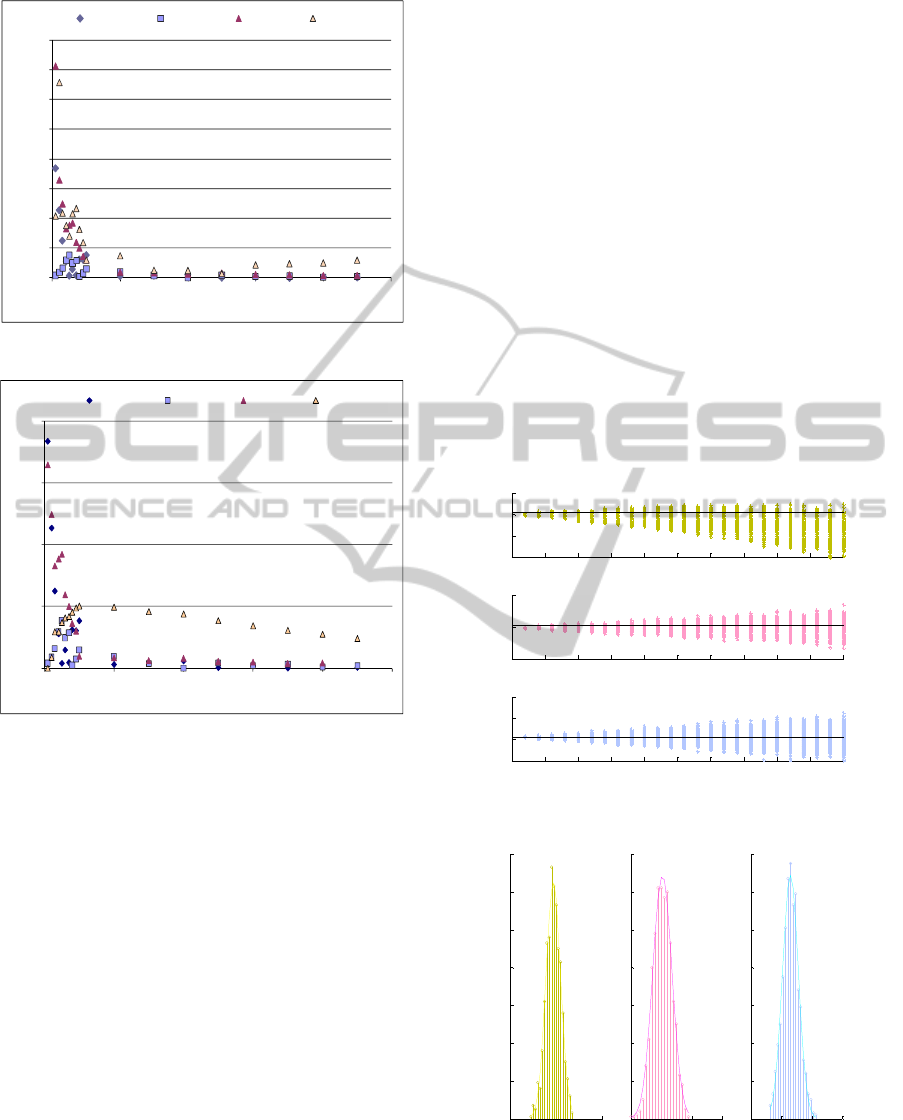
Figure 5: Relative errors by algorithm, for the PP probe.

Figure 6: Relative errors, by algorithm, for the APD probe.

While the PP probe exhibits lower than 8% error,

the APD one never exceeds the 4% limit.

Cross-correlation (Fcorr version) can be

identified as the best performing algorithm with a

relative error never exceeding 1% in any probe.

In the APD probe, the phase angle detection

method also yields very good (lower than 1%) error,

but poor performance for the PP probe, mainly in the

small time lag region.

As expected all the algorithms performed almost

perfectly for higher than 10ms time delays.

5.3 Noise Tolerance

Robustness of the algorithms to noise is assessed by

adding normal distribution noise to the photodiode

readings and studying the resulting effect on the

algorithm output.

This test was performed just for the correlation

and phase methods. It was not used in foot-to-foot

detection, because, as long as added noise is of the

order of magnitude of the threshold used to detect

the upstroke, the upstroke will not be detected at all.

Data collected by the PP and APD probes was

submitted to this test using the following procedure:

for each noise level, the algorithm under test was run

1000 times, with an independent noise vector

affecting every run.

In total, 25 relative noise levels, from zero to 0.5

of peak amplitude, were explored.

Figures 7 to 12, enclosing the full information of

this test, are shown side by side to make

comparisons easier.

Figures 8 and 9 show the dispersion introduced

by noise for a reference delay of 4.1 ms. The

resulting PTT values, taken as the mean value of

each distribution, are plotted in Figure 9. While

these figures concern the PP probe, Figures 10, 11

and 12 represent the same study for the APD probe.

As mentioned before, noise is expressed as a

fraction of the peak amplitude of the signal.

Figure 7: Dispersion introduced by noise in the PP probe.

Figure 8: PTT dispersion plots for each algorithm, for a

relative noise level of 0.14. The gaussian fittings stress the

normal nature of the distributions.

0 0,02 0,04 0,06 0,08 0,1

Erro r [%]

Reference Time Delay [sec]

Xcorr Fcorr Foot Phase

0 0,02 0,04 0,06 0,08 0,1

Error [%]

Reference Time Delay [sec]

Xcorr Fcorr Foot Phase

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5

x 10

-3

Xcorr

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5

x 10

-3

Fcorr

Time [sec]

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5

x 10

-3

Phase

Relative noise

3.5 4 4.5 5

x 10

-3

100

120

140

Time [sec]

Phase

3.5 4 4.5 5

x 10

-3

100

120

140

Time [sec]

Fcorr

3 4 5

x 10

-3

100

120

140

Time [sec]

Xcorr

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

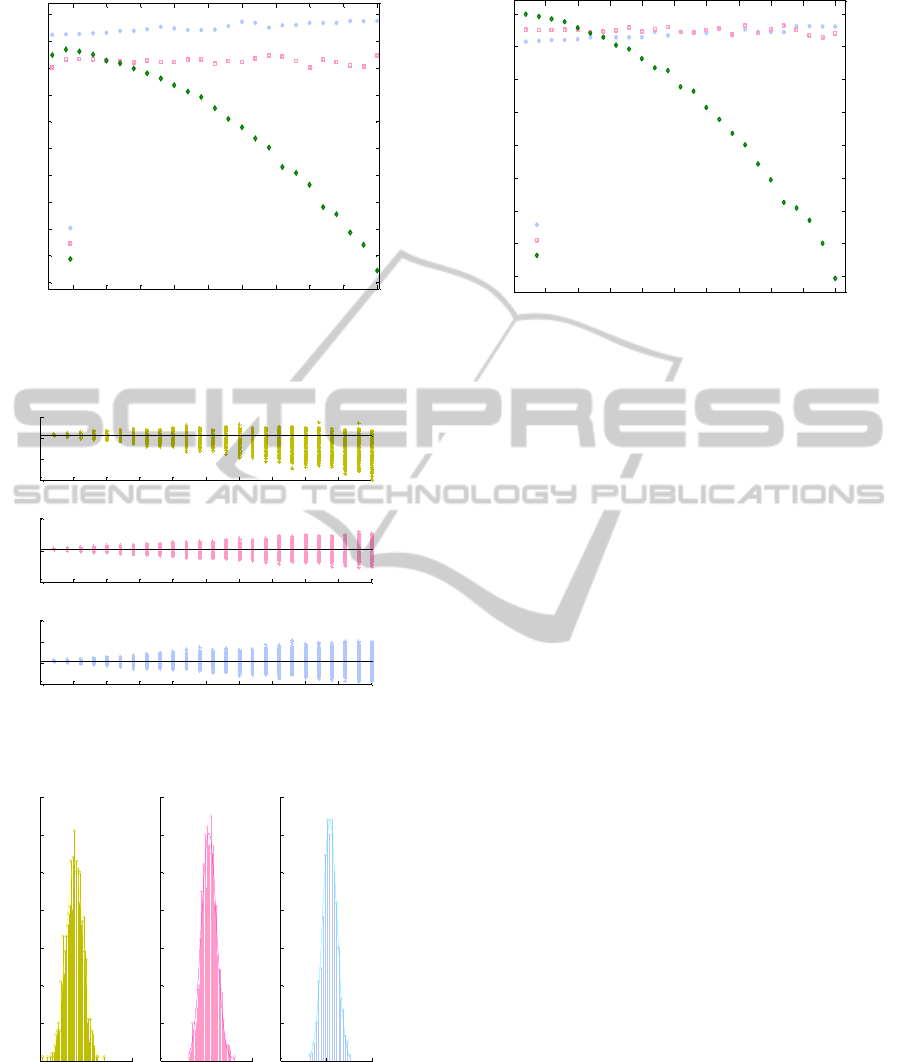
Figure 9: Mean of distribution vs. relative noise for a 4.1

ms reference delay in the PP probe.

Figure 10: Dispersion introduced by noise for the APD

probe.

Figure 11: PTT dispersion plots for each algorithm, for a

relative noise level of 0.14. The gaussian fitting stresses

the normal nature of the distribution.

Figure 12: Mean of distribution vs. relative noise for a 4.1

ms reference delay in the APD probe.

Not surprisingly, the dispersion introduced by

adding noise is also gaussian with variance

proportional to the noise level (Figures 8 and 11).

However, different robustness to noise is

exhibited by each of the three tested algorithms, with

the phase and Fcorr methods showing the lowest

errors when subject to high levels of noise.

It is also clear that the Xcorr based algorithm is

not robust to noise and, under high noise conditions

it shows a strong tendency to under-evaluate PTT, as

shown in Figures 9 and 12.

The phase method exhibits the higher levels of

robustness since its median remains constant for

high noise levels and, in addition, the corresponding

distribution shows the lower variance. The large

offset yielded by this algorithm in the PP probe (but

not in the APD probe) is rather puzzling and is

probably associated to the particular shape of PP

signals which, very much unlike the APD, are

conditioned by the large equivalent capacity of the

photosensor.

Another clarifying way to look at the overall

performance of probes and algorithms is shown in

Figure 13 where the probabilities of the algorithm

returning a PTT value with less than 5% and less

than 10% error are plotted against noise. Results,

expressed as a percentage, are derived from 1000

runs per curve.

Data in Figure 13 confirms the superior

robustness of the phase method.

0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5

3.2

3.3

3.4

3.5

3.6

3.7

3.8

3.9

4.1

4.2

x 10

-3

Relative noise

Time [sec]

Phase

Fcorr

Xcorr

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5

x 10

-3

Xcorr

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5

x 10

-3

Fcorr

Time [sec]

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5

x 10

-3

Phase

Relative noise

2 4 6

x 10

-3

100

120

140

Time [sec]

Phase

2 4 6

x 10

-3

Time [sec]

Fcorr

2 4 6

x 10

-3

Time [sec]

Xcorr

0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0. 45 0.5

3.4

3.5

3.6

3.7

3.8

3.9

4.1

4.2

x 10

-3

Relative noise

Time [sec]

Phase

Fcorr

Xcorr

OPTICAL METHODS FOR LOCAL PULSE WAVE VELOCITY ASSESSMENT

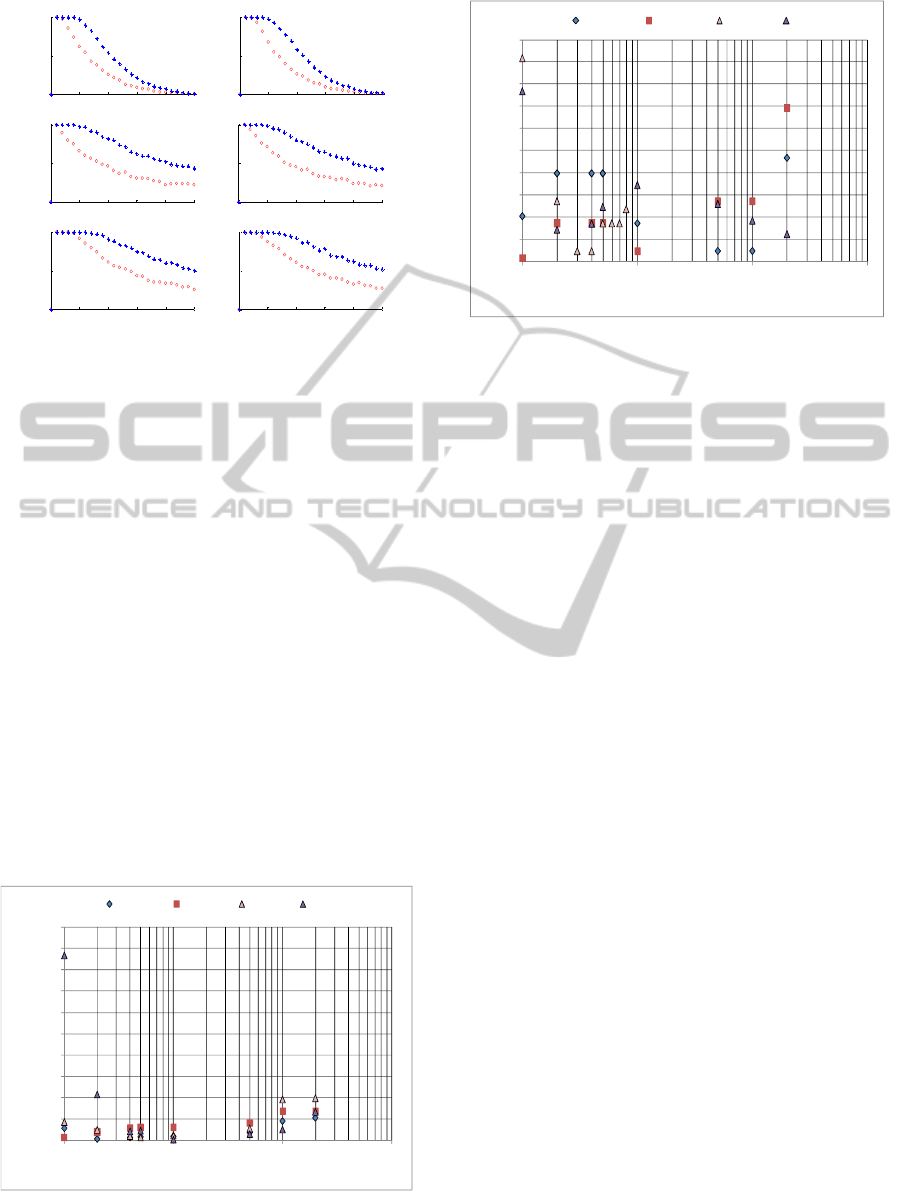
Figure 13: Measurements with less than 5% error (blue

dots) and less than 10% error (red circles) vs. relative

noise.

As can be stated, all algorithms can deliver 100%

measurements within the specified error threshold,

up to a certain noise level, where the curves show a

turning point and start decaying towards zero. The

phase algorithm not only shows a higher turning

point but also decays much slowly as noise

increases, denoting extra robustness to noise.

5.4 Algorithm Robustness

A final test was carried out in order to study the

effect of different heart rates on the performance of

the algorithms. In fact, all the data mentioned so far

was acquired at a rate of 1 pulse per second, thus,

any conclusive notes might not be valid for other

acquisition rates. Accordingly, the referred test was

performed for signal repetition rates varying from 1

to 200 Hz, without artificial noise added to the

readings and for a known constant time delay.

Figure 14: Plot of the relative errors for each algorithm for

a range of frequencies of signal, for the PP probe.

Figure 15: Plot of the relative errors for each algorithm for

a range of frequencies of signal, for the APD probe.

The value used for the time delay, 1.1 ms, was

selected by mere convenience. At this point it’s not

unimportant to remark that the AWG2 (Figure 1)

can define the time delay as an angle, the delay

angle, with a precision of a tenth of a degree; on the

other side, for the specific used set of repetition

rates, the value of 1.1 ms yields feasible values for

delay angles that, otherwise, could not be loaded by

the equipment.

In conclusion, as Figures 14 and 15 reveal, the

APD probe performs superiorly (note that the

vertical scales of the figures are different). It is also

noticeable that the Fcorr and the phase algorithms

produce the best results if the entire range of

repetition rates is considered.

6 CONCLUSIONS

Two optical probes specifically designed to measure

PTT have been developed and tested along with

three different signal processing algorithms.

Tests show that although both probes are capable

of measuring PTT accurately, the APD based one is

more precise and accurate.

All three tested algorithms can measure PTT

with an error below 8%. Nevertheless, just the one

designated by Fcorr exhibits the capability of

measuring PTT with an error bellow 1%, for the

complete range of delays. The phase method shows

the higher levels of robustness to noise.

When the signal repetition rate spans over a large

range of values, the Fcorr algorithm can deliver

PTTs with the lowest errors.

The natural follow-up of this work will be start

acquiring pulse data in humans. Figure 16 shows a

preliminary acquisition in human using the APD

0 0.1 0.2 0.3 0.4 0.5

100

PPD - Xcorr

0 0.1 0.2 0.3 0.4 0.5

100

PPD - Fcorr

Time [sec]

0 0.1 0.2 0.3 0.4 0.5

100

PPD - Phase

Relative noise

0 0.1 0.2 0.3 0.4 0.5

100

APD - Xcorr

0 0.1 0.2 0.3 0.4 0.5

100

APD - Fcorr

0 0.1 0.2 0.3 0.4 0.5

100

APD - Phase

Relative noise

10%

20%

30%

40%

50%

60%

70%

80%

90%

100%

1 10 100 1000

Error [%]

Repetition rate [Hz]

Xcorr Fcorr Foot Phase

10%

12%

14%

16%

18%

20%

1 10 100 1000

Error [%]

Repetition rate [Hz]

Xcorr Fcorr Foot Phase

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

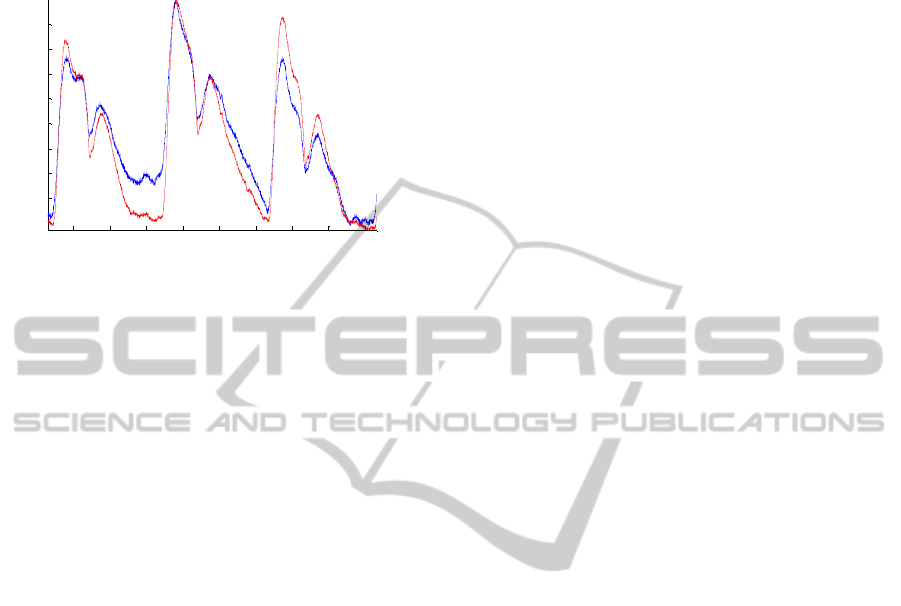
probe. The shape of the pulses is very clear, not to

much affected by noise and allows the anticipation

of good results.

Figure 16: Preliminary results of the APD probe acquiring

data in humans.

ACKNOWLEDGEMENTS

The authors acknowledge the support from

Fundação para a Ciência e Tecnologia (FCT) for

funding (PTDC/SAU-BEB/100650/2008).

REFERENCES

Laurent S, et al., 2006. Expert consensus document on

arterial stiffness: methodological issues and clinical

applications Eur Heart. J. 27 2588-2605.

Kips J, et al., 2010. The use of diameter distension

waveforms as an alternative for tonometric pressure to

assess carotid blood pressure. Physiol. Meas. 31

(2010) 543–553.

Vermeersch S. J. et al., 2008. Determining carotid artery

pressure from scaled diameter waveforms: comparison

and validation of calibration techniques in 2026

subjects. Physiol. Meas. 29 1267–80.

Minnan Xu, 2002 Local Measurement of the Pulse Wave

Velocity using Doppler Ultrasound. Massachusetts

Institute of Tecnology.

Bramwell J. and Hill A., 1922. The velocity of the pulse

wave in man. Proc Roy Soc Lond [Biol]. 93 298-306

Nichols, W. and O’Rourke, M. F., 2005. McDonald’s

Blood Flow in Arteries: Theoretical Experimental and

Clinical Principles. 5th ed., London.

Rajzer M. et al., 2008. Comparison of aortic pulse wave

velocity measured by three techniques: Complior,

Spymocor and Arteriograph. J. Hypertens. 26

2001:2007.

Azaria M. and Hertz D., 1984. Time delay estimation by

generalized cross correlation methods. IEEE Trans.

Acoustics, Speech, and Signal Processing, vol. ASSP-

32, pp. 280-285.

Kazanavicius E. and Gircys R., 2005. Mathematical

Methods for determining the foot point of the Arterial

Pulse Wave and Evaluation of Proposed Methods.

ISSN 1392 – 124X Information Technology and

Control.

0.5 1 1.5 2 2.5 3 3.5 4 4.5

x 10

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Time [sec]

A.U.

OPTICAL METHODS FOR LOCAL PULSE WAVE VELOCITY ASSESSMENT