
BINDING FREE ENERGY CALCULATION VIA MOLECULAR
DYNAMICS SIMULATIONS FOR A miRNA:mRNA INTERACTION
G. Paciello, A. Acquaviva, E. Ficarra, M. A. Deriu, A. Grosso and E. Macii
Dep.of Control and Computer Engineering and Dep.of Mechanics, Politecnico di Torino
C.so Duca degli Abruzzi 24, Torino, Italy
Keywords:
miRNA, Molecular dynamics, Thermodynamic integration.
Abstract:
In this paper we present a methodology to evaluate the binding free energy of a miRNA-mRNA complex
through Molecular Dynamics-Thermodynamic Integration simulations. We applied our method on the C −
elegans let-7 miRNA:lin-41 mRNA complex, known to be a validate miRNA:mRNA interaction, in order
to evaluate the energetic stability of the structure. The methodology has been designed to face the various
challenges of nucleic acid simulations and binding free energy computations and to allow an optimal trade-off
between accuracy and computational cost.
1 INTRODUCTION
MicroRNAs (miRNAs) are endogenously produced
21 ÷ 23-nt long riboregulators implicated in the con-
trol of biological processes such as differentiation,
cell proliferation and developmental timing(Bartel,
2004)(Cevec et al., 2008). MiRNAs’ target predic-
tion is an interesting field of research widely investi-
gated in the last years. Currently almost all the ex-
isting miRNAs’ target prediction algorithms consider
only general principles based on secondary structure
analyses.
In the present work, we propose a study of the ener-
getic stability of a specific experimentally validated
interaction(Vella et al., 2004), that is the bound be-
tween C − elegans let-7 miRNA fragment and its
complementary site LCS2 in the 3
′
UTR of the lin-
41 mRNA(Cevec et al., 2008), by calculating their
binding free energy via Molecular Dynamics (MD)-
Thermodynamic Integration (TI) simulations.
The contribution of this work is twofold. First, we
devise a methodology for the computation of the free
energy of this interesting class of RNA strands, also
taking into account the computational costs. Second,
thanks to the MD simulations, we highlighted the rel-
evance of tridimensional structure informations on the
free energy result.
2 MATERIALS AND METHODS
2.1 System Set-up
The original NMR let-7:lin-41 atomic struc-
ture(Cevec et al., 2008) was taken from the Protein
Data Bank (PDB) with accession code 2JXV and
then modified to better mould the interaction between
miRNA and mRNA pointed out in nature(Vella et al.,
2004).
The secondary structure so obtained is shown in Fig-
ure 1.
Figure 1: let-7 miRNA:lin-41 mRNA modified model. The
dot represents a wobble base pair.
The modified complex was solvated in a cubic box
with 12000 TIP4P water molecules to avoid dis-
tortions(Cheatham, 2004) and then its negative net
charge neutralized with 27 sodium ions. The coor-
dinates were optimized via 3 ps steepest descendent
energy minimization, after which an all atom position
restrained simulation for 5 ps under a constant force
of 1000 kJmol
−1
nm
−2
was carried out. All the sim-
ulations were performed using the ffamber94 Force
Field(Cornell et al., 1995) that we integrated in Gro-
318
Paciello G., Acquaviva A., Ficarra E., A. Deriu M., Grosso A. and Macii E..
BINDING FREE ENERGY CALCULATION VIA MOLECULAR DYNAMICS SIMULATIONS FOR A miRNA:mRNA INTERACTION.
DOI: 10.5220/0003167703180321
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2011), pages 318-321
ISBN: 978-989-8425-36-2
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

macs 4.0.5 distribution(Van Der Spoel et al., 2005).
2.2 Molecular Dynamics Simulations
A preliminary set of MD simulations was conducted
to check the conformational stability of the molecular
system and to select the best simulation parameters to
adopt in the subsequent free energy simulations. Due
to the well known helix shape modifications(Pan and
Mackerell, 2003), the first and the last nucleotides of
both RNA chains were restrained with a force con-
stant of 1000kJmol
−1
nm
−2
. The temperature was
maintained constant at 310K and all bonds were kept
rigid thanks to the LINCS Algorithm. Non bonded
interactions were calculated using a neighbor list up-
dated every 5 time steps. Cut-off distance for short-
range interactions was set at 1.2nm. Fast Particle-
Mesh Ewald electrostatics (PME) in all the three di-
mensions was used to calculate long-range electro-
static forces. The interpolation order for PME was
set as cubic whereas the relative strength of Ewald-
shifted direct potential at Coulomb distance at 10
−5
.
A leap-frog algorithm was used for integrating New-
ton’s equations of motion. Trajectory structures were
saved at 0.1ps intervals from a 1ns and a 10ns long
molecular dynamics simulations.
2.3 Free Energy Calculations
Thermodynamic-Integration (TI) approach was used
to calculate the binding free energy. The TI technique
allows to obtain the free energy difference ∆G be-
tween two states of a system, A described by a Hamil-
tonian H(λ = 0) = H
A
and B defined by a Hamiltonian
H(λ = 1) = H
B
, by changing from A to B state the in-
teraction parameters that define the Hamiltonian H as
a function of a coupling parameter λ as showed in Eq.
1.
∆G
BA
= G
B
− G
A
=
Z
1
0
dG(λ)
dλ
dλ =
Z
1
0
h
dH(λ)
dλ
i
λ
dλ
(1)
The thermodynamiccycle implemented to achieve the
desired binding free energy value is reported in Figure
2(Lawrenz et al., 2009).
In order to achieve the conditions described by the
thermodynamic cycle, the B state of the system was
opportunely edited during the simulations. At any in-
termediate state the Hamiltonian of the system was
defined by Eq. 2.
H(λ) = (1− λ)H
A
+ λH
B
(2)
Regarding Eq. 2, the ensemble averages of the deriva-
tive of the Hamiltonian were calculated via 1ns long
∆G
BIND
= ∆G
2
− ∆G
1
Figure 2: Thermodynamic cycle used in binding free en-
ergy calculations. The two branches of the cycle have to
be considered in order to obtain the free energy of binding
between the ligand, mRNA, and the receptor miRNA.
constrained MD simulations at the constant pressure
of 1atm. The averages of the derivatives, obtained
from the simulations, were then integrated giving rise
to ∆G
1
(Figure 2) and ∆G
2
(Figure 2). The binding
free energy was then calculated by subtracting the first
quantity to the second as synthesized in Figure 2.
3 RESULTS AND DISCUSSION
3.1 Molecular Dynamics
The stability of let-7:lin-41 complex, known to be
strictly depending on several elements(Cheatham,
2004), was evaluated via the atom positional-RMSD
analysis in the unconstrained MD trajectory struc-
tures from the initial molecular configuration. Let-7
miRNA, called ’Chain A’, showed an average RMSD
value of 0.281nm and a maximum RMSD value of
0.421nm after about 887ps of simulation. Lin-41
mRNA, called ’Chain B’ presents, instead, a higher
RMSD mean value of about 0.389nm, and a remark-
able deviation from the initial trajectory in the first
part of the run.
To maintain the original helix shape during the
run the atomic fluctuations of about 30 atoms (one
nucleotide) at the beginning and at the end of the
strands were limited: In this manner the RMSD aver-
age value for Chain A is 0.136nm whereas for Chain
B is 0.167nm. The achieved stability of the complex
was analyzed also via a 10ns long simulation. In this
case the maximum RMSD value obtained is 0.214ns
after 5090ps of running. The choice to adopt re-
BINDING FREE ENERGY CALCULATION VIA MOLECULAR DYNAMICS SIMULATIONS FOR A miRNA:mRNA
INTERACTION
319

(a)
(b)
Figure 3: Model and explanation of the molecular system during the constrained simulation. In Subfigure (a) is reported a
scheme of the constrained molecular complex and in Subfigure (b) the summarize of the restraints applied.
straints, sketched and summarized in Figure 3 (a) and
(b), was considered plausible by taking into account
previous biological researches(Schwarz and Zamore,
2002)(Vella et al., 2004).
3.2 Free Energy Calculations
The binding free energy values were obtained by
starting from a number of lambda set to 11 and by in-
crementing it progressively until (for a fixed number
of lambda) the percentage error of the ensamble aver-
ages of the derivative of the Hamiltonian between two
successive lambda values was inferior to a threshold
set to 4% with respect to the total variation between
λ = 0 and λ = 1.
The criterion was satisfied for both ligand and
complex with 60 lambda values. In this sampling
conditions, the free energy for the branch relative to
the complex was equal to 4043, 57kcal/mol whereas
for the ligand it was 3939, 32kcal/mol. As such,
the final binding free energy value obtained was
−104, 25kcal/mol. We noticed however that starting
from 51 lambda values the error is clearly reaching
an asintotic behaviour with percentage errors around
2%.
This aspect was further investigated by consider-
ing the accuracy of the free energy results obtained
with respect to the error achieved using 60 lambda
values, for which the threshold error criterion is satis-
fied: We noticed that a very good accuracy is reached
already with 19 lambda, the percentage error is about
7% and a further improvement is obtained with 51
lambda, the error is here about 0.25%.
3.3 Scalability Analysis
In the following we report about the characterization
of the stability of the binding free energy computa-
tions on a Symmetric Multiprocessing (SMP) archi-
tecture, namely a 4+4 Intel(R) Core(TM) i7 CPUs
920 @ 2.67GHz machine. The simulations for var-
ious lambdas were implemented as independent pro-
cesses. The experiments were conducted using the set
up of the TI-MD simulations previously discussed,
but with a length reduced to 5ps since by profiling
the short and long simulations we observed the same
characteristics in terms of system resource utilization
(i.e. percentage of memory and cache accesses). We
run 2, 4, 8, 12, 16, 24, 32 and 64 parallel simula-
tions during which the average percentage CPU user
utilization for the processes was recorded by taking
advantage of the command pidstat of the Sysstat util-
ities. We will report here only the obtained CPU user
utilization statistics, because the system utilization for
the processes was found to be negligible. As it is
shown by trace ’I’ of Figure 4, the real trend of the
average CPU utilization for the processes is very dif-
ferent from the ideal one of Figure 4 trace ’II’, ob-
tained by assuming a perfect independence between
processes, that is the simulation time is independent
from the number of lambdas: Even if we increase
the number of simulations and thus the workload im-
posed to the system, the simulation time remains con-
stant until the number of CPU is larger or equal to
the number of processes. Then it increases in a lin-
ear way. Trace ’I’ is far from the ideal behavior, as
the simulation time increases as a function of lambda.
This is mainly due to two effects. The first effect is
the impact of memory congestion. Indeed, even if the
processes do not communicate or use shared memory
BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms
320
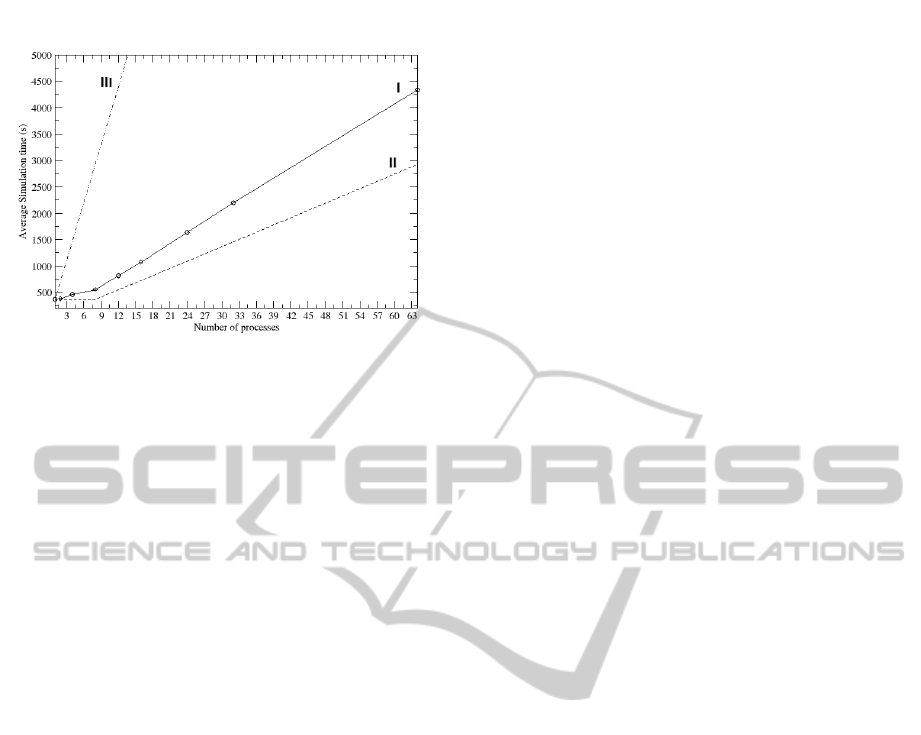
Figure 4: Trend of the simulation time at the increasing
of the running processes. Trace ’I’ and ’II’ are respec-
tively the real and the ideal trend for the simulation time
obtained by running an increasing number of parallel pro-
cesses, whereas trace ’III’ is that relative to an increasing
number of serial processes. The cycles on Trace ’I’ mark
the number of processes for which the test have been made.
regions, there is a considerable contention for access
to the L2 cache and the main memory. The latter
arises when the number of processes overcomes the
number of available CPUs. Indeed, it can be observed
that trace ’I’ is characterized by two different trends.
The first one, from 1 to 8 lambda, where only the
memory contention contributes. The second, from 8
to 64 lambda, where the context switch and process
migration overheads are also present, leading to an in-
creasing slope of the curve. The utilization is almost
100% before 8 lambda and decreases after 8 lambda,
where each process has to share the CPU with others.
It is worth nothing however that besides the overhead
discussed, the parallelization is unquestionably more
advantageous with respect to performing serial simu-
lations, whose simulation times are reported in Trace
’III’ of Figure 4. Overall, by putting together the
accuracy results with the computation costs, we can
conclude that a suitable trade-off between computa-
tion and accuracy can be set to 19 lambda.
4 CONCLUSIONS
The methodology presented in this paper has been de-
signed to face the various challenges of nucleic acid
simulations and binding free energy computations.
First, the positioning of the restraints has been deter-
mined to overcome the stability problems due to the
remarkable folding activity and the base pairs open-
ing of the complex. As a results, we were finally able
to perform MD simulations in stable conditions.
Second, the accuracy of the thermodynamic inte-
gration steps. On this concern, we studied the scala-
bility of the thermodinamic integration to determine a
reasonable trade-off between computation and accu-
racy. We shown that to achieve an error on the bind-
ing free energy computation lower than 4% we need
to perform 60 parallel simulations. On the other side,
a good trade-off between computation and accuracy
is already reached using 19 parallel simulations.
REFERENCES
Bartel, D. P. (2004). MicroRNAs: Genomics, Biogenesis,
Mechanism, and Function. Cell.
Cevec, M., Thibaudeau, C., and Plavec, J. (2008). Soluc-
tione structure of a let-7 miRNA:lin41 mRNA com-
plex from C.elegans. Nucleic Acids Research.
Cheatham, T. E. (2004). Simulation and modelling of nu-
cleic acid structure, dynamics and interactions. Cur-
rent Opinion in Structural Biology.
Cornell, W. D., Cieplak, P., Bayly, C. I., Gould, I. R., Merz,
K. M., Ferguson, D. M., Spellmeyer, D. C., Fox, T.,
Caldwell, J. W., and Kollman, P. A. (1995). A second
generation force field for the simulation of proteins,
nucleic acids, and organic molecules. J. Am. Chem.
Soc.
Lawrenz, M., Baron, R., and McCammon, J. A.
(2009). Independent-trajectories thermodynamic-
integration free-energy changes for biomolecular sys-
tem: Determinants of N5HN1 Avian Influenza Virus
Neuraminidase Inhibition by Peramivir. Journal of
Chemical Theory and Computation.
Pan, Y. and Mackerell, A. D. (2003). Altered structural
fluctuations in duplex RNA versus DNA: a confor-
mational switch involving base pair opening. Nucleic
Acids Research.
Schwarz, D. S. and Zamore, P. D. (2002). Why do miRNAs
live in the miRNP? Genes e Development.
Van Der Spoel, D., Lindahl, E., Hess, B., Groenhof, G.,
Mark, A. E., and Berendsen, H. J. C. (2005). GRO-
MACS: Fast, flexible, and free. Journal of computa-
tional chemistry.
Vella, M. C., Reinert, K., and Slack, F. J. (2004). Ar-
chitecture of a validate microRNA::target interaction.
Chemistry e Biology.
BINDING FREE ENERGY CALCULATION VIA MOLECULAR DYNAMICS SIMULATIONS FOR A miRNA:mRNA
INTERACTION
321
