FREQUENCY CHARACTERIZATION OF A MAGNETICALLY

ACTUATED MEMS RESONANT BIOSENSOR

V. Russino, F. Pieri

Dipartimento di Ingegneria dell’Informazione, Universit

a di Pisa, Via G. Caruso 16, 56122 Pisa, Italy

D. Paci

STMicroelectronics, Via Tolomeo 1, 20010 Cornaredo, Italy

Keywords:

Biosensors, Resonant sensors, Microbalances, MEMS.

Abstract:

In this work, the mass response of a resonant, CMOS (Complementary MOS) compatible MEMS sensor,

oriented at the detection of diagnostic markers, is presented. The sensor is fabricated with a MEMS (Micro-

electro-mechanical System) post-processing method on a standard, CMOS-based VLSI technology, retaining

maximum compatibility with the CMOS process ﬂow. The mechanical resonator is based on inductive actu-

ation and detection, and the sensing is based on the microbalance principle. A protocol for covalent bonding

of organo-functional silanes (to be used as link sites for biomolecular probes) on the resonator surface is pre-

sented. The effect on the mechanical frequency response of a test mass attached to the surface is demonstrated

by grafting of gold nanoparticles (NP’s) to the amino-terminated surface silanes.

1 INTRODUCTION

MEMS resonators have been proposed as biosensors

based on the gravimetric principle, trying to trans-

fer the approach of the ubiquitous Quartz Crystal Mi-

crobalance (QCM) to the MEMS domain. Miniatur-

ization of resonant biosensors could lead to several

advantages: reduced amount of biological samples,

possibility of integration of multiple sensors on a sin-

gle substrate (sensor arrays), potential for the inte-

gration of conditioning electronics on the same chip,

with consequent improved SNR and, in turn, sensi-

tivity. While the fabrication of piezoelectric MEMS

resonant sensors (the microscopic counterpart of the

QCM) is certainly possible (Zuniga et al., 2009),

other transduction mechanisms are accessible in the

MEMS world: for example capacitive (Teva et al.,

2006), piezoresistive (Sone et al., 2004), each with

advantages and drawbacks.

A few speciﬁc issues must be addressed in the de-

sign of a feasible MEMS resonant biosensor: the de-

vice (and its package) must withstand operation in a

liquid environment (a severe requirement, for exam-

ple, in capacitive MEMS resonators which are prone

to stiction, i.e. elastocapillary collapse (Maboudian

and Howe, 1997); the functionalization protocol of

the resonator surface must be compatible with other

on-chip components (metal lines used for electric sig-

nal distribution, on-board electronics, etc.) (Lenci

et al., 2010). In this work, we addressed these issues

by developing a MEMS torsional resonator with mag-

netic driving and sensing.

The high torsional stiffness and large cavity un-

der the moving parts eliminates the stiction problem,

while a carefully designed silanization protocol al-

lows for reliable operation of the sensor. In the fol-

lowing, after a description of the design, MEMS fab-

rication and functionalization methods, we present

a full electrical characterization of the resonators in

terms of its frequency response.

The operation of the resonator as a microbalance

is demonstrated by anchoring gold NP’s on the res-

onator surface and measuring the consequent shift in

resonance frequency. A discussion of the experimen-

tal data is then carried out, and an estimate of the sen-

sor mass sensitivity is presented.

2 DESIGN AND FABRICATION

The proposed MEMS sensor is based on a torsional

resonator, whose overall structure is sketched in Fig.1

391

Russino V., Pieri F. and Paci D..

FREQUENCY CHARACTERIZATION OF A MAGNETICALLY ACTUATED MEMS RESONANT BIOSENSOR.

DOI: 10.5220/0003167803910396

In Proceedings of the International Conference on Biomedical Electronics and Devices (BIODEVICES-2011), pages 391-396

ISBN: 978-989-8425-37-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Sketch of the sensor structure.

(Paci et al., 2008). A square plate with a central hole

(the hole is required for fabrication purposes, see sec-

tion 2.2) is suspended over a cavity etched on a crys-

talline silicon substrate by means of two thin beams,

acting as torsional springs. Two separate, concentric

inductors (in red and light blue in Fig.1) are embed-

ded in the plate, while the electrical connections to the

inductors are embedded in the suspending beams.

To drive the plate into mechanical resonance, an

external static magnetic ﬁeld (provided, for example,

by a permanent magnet) is required. An alternating

current injected in one of the inductors (the driving

loop) generates Lorentz forces on two sides of the

loop, and the resulting mechanical torque drives the

plate into oscillation, whose amplitude is only signif-

icant (a few degrees at its maximum) if the frequency

of the driving signal is close to or exactly at the me-

chanical resonance frequency of the structure.

Because of the external magnetic ﬁeld, an EMF

(electromotive force) at the same frequency of the

input current is induced on the second inductor (the

sensing loop). The amplitude of this EMF is signiﬁ-

cant only at the resonance frequency, so that the de-

vice effectively acts as a frequency selective system

(a resonant ﬁlter). A parasitic voltage component,

caused by mutual inductance between the two induc-

tors, is also present at the output.

The surface of the plate is biochemically activated

by covalent bonding of an organo-functional silane

layer, with a protocol which retains CMOS com-

patibility with other on-board components (including

electronic circuits). The functional group of the silane

molecule can be used to link bioreceptors, which in

turn bind speciﬁcally with the target biomolecule.

The resulting shift in mass can be measured by the

consequent shift in the resonance frequency with an

all-electrical measurement system. It this work, gold

nanoparticles (NP’s) (Diegoli et al., 2006) anchored to

amino terminal groups of the silane molecules were

used as the test mass to demonstrate the viability of

the transduction mechanism.

2.1 Magneto-mechanical Modelling

Despite being a distributed parameter system, the de-

vice depicted in Fig.1 can be described with reason-

able accuracy by a reduced model by treating it as a

lumped parameter mechanical resonator, governed by

an ordinary differential equation:

θ + D

θ + kθ = Γ

(t) (1)

where θ is the rotation angle of the plate, J is its the

rotational moment of inertia, D is a damping coef-

ﬁcient (mostly caused by viscous losses in the sur-

rounding air), k is a torsional spring constant, Γ

is the input magneto-mechanical coupling coefﬁcient

(proportional to the external magnetic ﬁeld) (Tilmans,

1996), and i

is the driving current.

The mechanical resonance frequency f of the sys-

tem is thus f

= 1/2π ·

k/J. Theoretical and sim-

ulated resonance frequencies for our devices are in

the 25 ÷100 kHz range. A straightforward analysis

shows that in presence of an additional surface mass

density µ

(caused by the analyte captured at the plate

surface), the resonance frequency undergoes a relative

shift equal to:

∆ f

= −

(2)

where t

and ρ

are the plate thickness and volume

mass density, respectively.

From the electrical point of view, a complete

equivalent two-port network can be developed for the

device (Paci et al., 2008). Its open circuit trans-

admittance (output voltage to input current transfer

function) is equal to:

H(s) =

(s)



1 +

Qω

+ Ms (3)

where Γ

and Γ

are input and output magneto-

mechanical coupling coefﬁcients, ω

= 2π f

is the

resonance angular frequency, Q =

√

kJ/D is the res-

onator quality factor, M is the mutual inductance be-

tween the two loops, and s is the generalized (com-

plex) angular frequency.

2.2 Device Fabrication

The devices process fabrication is based on the post-

processing of the STMicroelectronics BCD6s pro-

cess. The resonator plate is fabricated from the

BIODEVICES 2011 - International Conference on Biomedical Electronics and Devices

392

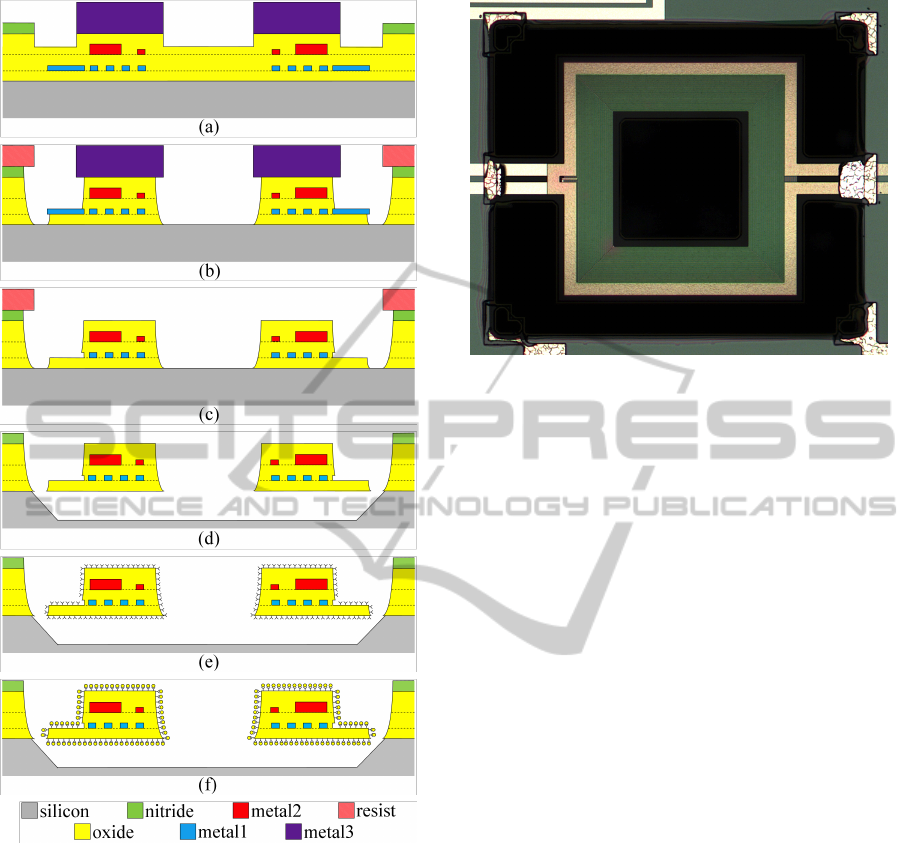
Figure 2: Sketch of the MEMS fabrication process (not to

scale). The single steps are described in the text.

inter-metal dielectric layers, while loops are fabri-

cated using the metal interconnection layers. A post-

processing sequence, designed to be CMOS compati-

ble, was used to release the microbalance.

The silicon chip section as received from the

foundry is shown in Fig.2a. The thick metal3 layer

(dark purple) is used as a mask to protect the res-

onator structure during the subsequent etch of the di-

electrics, basically silicon dioxide (yellow), while the

external structures (connection lines from and to the

loops, pads, etc.) are protected by a standard pho-

tolithographic resist (pink). The oxide is removed

in a buffered HF solution (Fig.2b) to reach the sili-

con substrate surface. At this point, the metal3 is not

Figure 3: Optical microscope photograph of one the fab-

ricated resonators. The plate side length is 400 µm. The

driving loop (yellow outer border) is clearly visible. The

dark area corresponds to the cavity in the silicon substrate.

required anymore and is then removed in a wet etch

(Fig.2c). The resist is removed as well, and the release

phase can be performed. During the release, carried

out in a buffered tetra-methyl-ammonium hydroxide

(TMAH) solution at 85

◦

C, the silicon under the plate

is anisotropically etched along (100) planes, so that

the plate and springs are mechanically detached from

the substrate. The chemistry of the TMAH solution

is tuned to allow etch of the silicon while removing

both the oxide and the metal negligibly (Biswas et al.,

2006). Because of the anisotropy, a central hole is

required in the plate to allow complete release of the

structure (Fig.2d). At this point, the resonators appear

as in Fig.3. The overall dimensions of a resonator is

(depending on the speciﬁc type) in the range of a few

hundreds of micrometers.

Once the mechanical structure of the resonator is

ready, the sample is glued to the ﬁnal, gold plated

ceramic package which will be used for electri-

cal characterization, and the silanization phase takes

place. Organo-functional silane deposition is com-

monly used as an intermediate step towards the cre-

ation of bioactive protein layers in biosensing appli-

cations. In this work, the silanization protocol devel-

oped in (Lenci et al., 2010) was tailored to suit the

needs of the speciﬁc application.

A preliminary cleaning of the sample in an ammo-

nia based solution (NH

OH(25%):H

O:H

(30%)

1:1:4 vol.) is performed. After 5

in the solution,

the sample is rinsed twice in deionized water (D.I.).

After this step, the resonator surface is terminated by

hydroxyl groups, which are required to allow covalent

bonding of the silane. While sulphuric acid-based so-

lutions (e.g. piranha) are most commonly used in the

FREQUENCY CHARACTERIZATION OF A MAGNETICALLY ACTUATED MEMS RESONANT BIOSENSOR

393

literature (Kim et al., 2008), they are not compatible

with exposed aluminium which is present in our sam-

ples at the external electric pads.

Immediately after rinsing, the sample is im-

mersed in an aqueous solution of 3-amino-propyl-

triethoxysilane (APTES) (0.05% vol.) for 5

, and

rinsed again in D.I. (Fig.2e). The sample then un-

dergoes a curing phase (Ballarin et al., 2008) by im-

mersion in acetone for 60

. During this phase, loosely

bound silane molecules or silane clusters are removed

and the overall quality of the silane layer improves.

At this point, the resonators are ready for charac-

terization. A single silicon chip contains up to four

resonators. The input and output inductors of each

resonator are bonded to the package gold contacts by

means of thin aluminum wires (Fig.4). A ﬁrst fre-

quency response of the resonator is measured using

the procedure detailed in the next section. To elimi-

nate the inﬂuence of ambient humidity (a common in-

terferer for gravimetric sensor), the sample is heated

in oven at 120

◦

C for 30

and immediately moved to

a sealed aluminium box for the electrical character-

ization. The resonators are then loaded with an ad-

ditional mass to verify their behaviour as gravimetric

sensor.

The added mass is represented by gold NP’s which

are known to bind to the exposed amino groups of the

silane layer. A 25 µl drop of a 30nm gold NP colloid

(British Biocell International) is deposed on the chip

(Fig.2f). After 60

, the sample is rinsed in D.I., dried

in oven (30

at 120

◦

C), and the frequency response

of the resonators is then measured again. To ensure

that the NP anchoring is speciﬁc to the silane layer, a

Figure 4: Photograph of a sensor chip mounted in its ce-

ramic package. Each chip contains four working resonators.

The bonding wires connecting the chip pads to the package

are also visible. The package side is 2.5 cm.

reference sample underwent the same procedure with

the exclusion of the silanization steps.

The amount of added mass was estimated by

Scanning Electron Microscope (SEM) observation of

the resonator front surface at several different test

sites (6 to 8 for each resonator). The number of NP’s

at each site, 1µm ×1 µm in size, was counted and

averaged. The resultant added mass density µ

was

calculated by supposing a constant diameter of 30nm

for each NP, and then multiplied by the total resonator

surface to obtain an estimate of the total added mass.

No trace of NP’s was found on the reference sample.

3 CHARACTERIZATION SETUP

The instrumentation setup for electrical characteriza-

tion is sketched in Fig.5. The input current is provided

by a waveform generator. The output voltage signal is

pre-ampliﬁed (the voltage level is in the hundreds of

microvolt range) and then fed to a lock-in ampliﬁer,

which measures the amplitude and phase relationship

between the input and the output signal. Both the

waveform generator and ampliﬁer are remotely con-

trolled by a personal computer.

The external magnetic ﬁeld is provided by two

permanent magnets. The ﬁeld amplitude is around

70mT. Before each measurement session, the sam-

ple is dried in oven (see section 2.2) and placed in

a sealed aluminium box. At least two measurement

sessions are performed for each resonator: one after

silanization, and one after NP grafting.

For each session, four different frequency curves

are measured: the ﬁrst, with a 20 kHz measure-

ment window centred at the theoretical resonance fre-

quency, obtained by FEM (Finite Element Method)

simulations, is used to identify the actual resonance

frequency peak. The other three measurements are

performed around the actual resonance frequency

with a 500 Hz window and a 5 Hz step. Each curve

requires between 10 and 30 minutes.

Moreover, as the magneto-mechanical coupling

coefﬁcients (Γ

and Γ

of Eq.3) are proportional to

the magnetic ﬁeld, a single response curve without

Figure 5: Schematic representation of the experimental

setup for electrical characterization.

BIODEVICES 2011 - International Conference on Biomedical Electronics and Devices

394

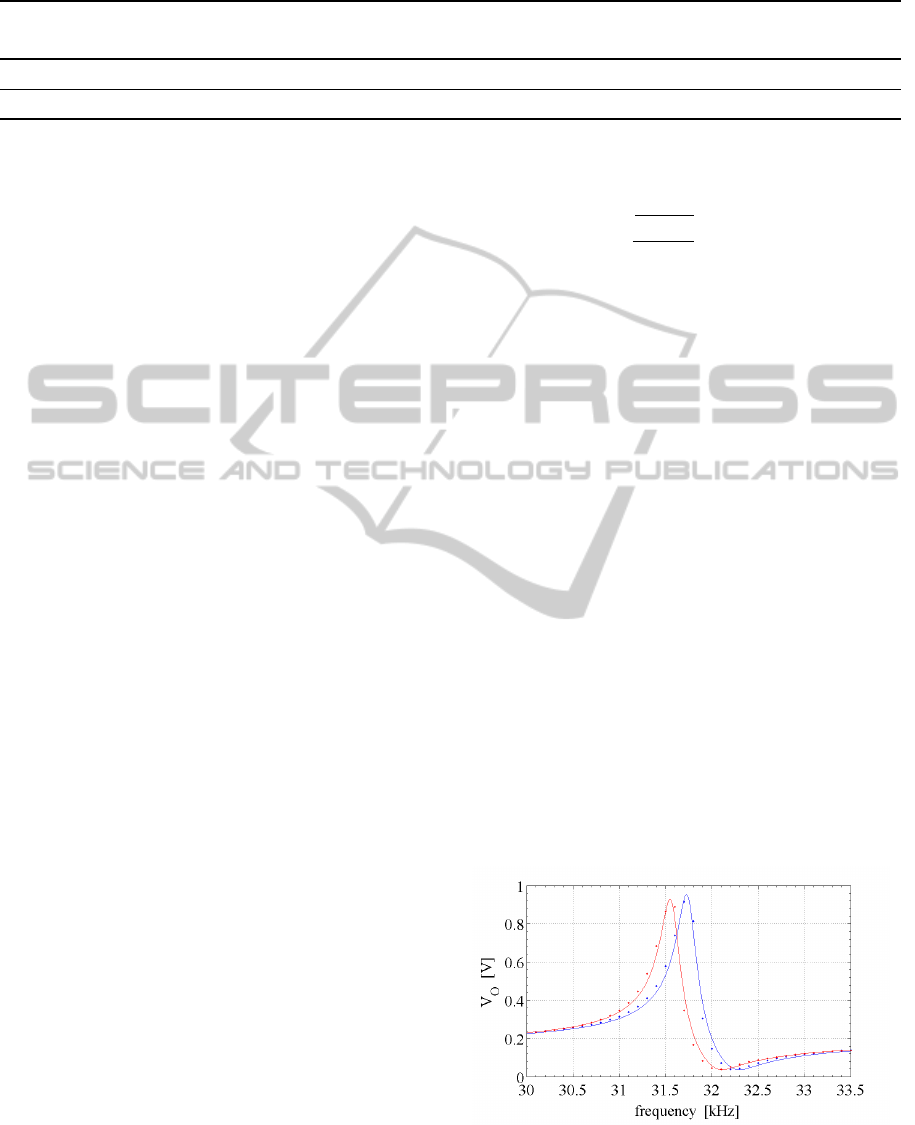
Table 1: Experimentally extracted parameters for two different resonators.

MB108

Q σ

[Hz] [Hz] [Hz] [Hz] [kg/m

] [kg/m

] [m

/kg]

200×200 94581 2.5 94291 2.5 287 1.26 3.67·10

−5

0.57·10

−5

−79.59

400×400 31749 1.0 31612 0.6 157 5.67 3.86·10

−5

1.31·10

−5

−117.27

magnets (and thus with Γ

= Γ

= 0) is also per-

formed on each resonator to extract the value of the

mutual inductive coupling coefﬁcient M.

The purely mechanical response (i.e. the ﬁrst term

in the RHS of Eq.3) is then extracted by subtraction of

the mutual inductance term from the actual measured

data. The obtained data points are then numerically

ﬁtted against the analytical expression of the mechan-

ical response to extract the most relevant mechani-

cal parameters, most importantly (from the applica-

tion point of view) the resonance frequency f and the

quality factor Q. For each resonator, their values are

averaged over the three measurements. Typical mea-

sured response curves are presented in Fig.6, where

the effect of the added mass on the resonance fre-

quency is also shown.

4 DISCUSSION AND

CONCLUSIONS

Typical extracted parameters from two different res-

onator types, fabricated on the same chip, are sum-

marized in Table 1. The MB108-400 resonator is

the device shown in Fig.3; the MB108-200 resonator

is a similar device, but with a smaller central plate

(200µm ×200 µm) and comparatively longer suspen-

sion springs. For each parameter, both the averaged

value (over three measures) and its standard deviation

(σ

∗

) are shown.

The initial resonance frequency f

was measured

immediately after silanization, and its value is af-

fected by very little error. The resonance frequency

after NP exposure, f

is consistently lower than the

initial frequency, and corresponds to a frequency shift

of a few hundred hertz (or 0.75% and 0.30% for the

two resonators, respectively). While the resonance

frequency tends to drift to higher values after a few

days on ambient storage (most likely because of ad-

sorption of ambient moisture), a drying step (30

120

◦

C) recovers its original value almost completely.

The frequency shifts must be compared to the

measured values of the added mass density µ

to ob-

tain an estimate of the sensor sensitivity. Given the

different area of the two devices, a sensitivity param-

eter allowing a fair comparison can be deﬁned as (Jan-

shoff et al., 2000):

S =

− f

−1

] (4)

The measured values for our resonators are around

79.6 and 117.3m

−1

for the two devices (Table 1,

last column). These values compare favourably to

the typical values for macroscopic QCM’s (about

−1

in (Janshoff et al., 2000)), but also to other

MEMS resonant sensors: (Zuniga et al., 2009), for

example, claims about 60 m

−1

. Compare also, for

a review, (Shen et al., 2010).

If the resonator plate thickness and density are

known, Eq.2 can be used to extract a theoretical value

of the mass density µ

S,T

from experimental frequency

shift data. If this analysis is carried out for our

devices, the theoretical mass density is consistently

higher than the measured one (by a factor of two or

more in some cases), with a correspondingly higher

value of the actual sensitivity S. Separate FEM anal-

ysis conﬁrms the trend implied by the simpliﬁed an-

alytical model used to obtain Eq.2, so that this dis-

crepancy cannot attributed to oversimpliﬁcation in the

mechanical model. Several other factors might come

into play in this case. Among them, the effect of the

NP adhesion on the residual (usually compressive)

stresses of the plate oxide ﬁlm (which are certainly

present due to fabrication issues and were neglected in

this analysis) and on the overall stiffness of the mem-

Figure 6: Frequency response of the resonator of Fig.3, be-

fore (blue) and after (red) NP grafting. Actual data are in-

dicated by the dots, while the lines are ﬁtted curves. The

contribution of the mutual inductance is not subtracted yet

(see text).

FREQUENCY CHARACTERIZATION OF A MAGNETICALLY ACTUATED MEMS RESONANT BIOSENSOR

395

brane (in particular in the torsional beams).

In conclusion, we demonstrated the operation

of a magnetically actuated MEMS resonator with

electrical input and output as a sensitive mass sen-

sor. The measured sensitivities can be compared

favourably to standard QCM’s and other imple-

mented MEMS microbalances. Moreover, a MEMS-

compatible silanization protocol for the resonator ac-

tive surface was developed as well. Such a silane

layer can be used as a precursor to the fabrication of a

bioactive layer to transform the device in a complete

resonant biosensor.

ACKNOWLEDGEMENTS

This work was partly ﬁnanced under a PRIN 2008

grant by the Italian Ministry for University and Re-

search.

REFERENCES

Ballarin, B., Cassani, M., Scavetta, E., and Tonelli, D.

(2008). Self-assembled gold nanoparticles modiﬁed

ito electrodes: The monolayer binder molecule effect.

Electrochim. Acta, 53:8034–8044.

Biswas, K., Das, S., Maurya, D., Kal, S., and Lahiri, S.

(2006). Bulk micromachining of silicon in tmah-based

etchants for aluminum passivation and smooth sur-

face. Microel. J., 37:321–327.

Diegoli, S., Mendes, P., Baguley, E., Leigh, S., Iqbal,

P., Diaz, Y. G., Begum, S., Critchley, K., Ham-

mond, G., Evans, S., Attwood, D., Jones, I., and

Preece, J. (2006). ph-dependent gold nanoparticle

self-organization on functionalized si/sio2 surfaces.

Journal of Experimental Nanoscience, 3:333–353.

Janshoff, A., Galla, H., and Steinem, C. (2000). Piezoelec-

tric mass-sensing devices as biosensors - an alternative

to optical biosensors? Angew. Chem. Int., 39:4004–

4032.

Kim, J., Seidler, P., Fill, C., and Wan, S. (2008). Investiga-

tions of the effect of curing conditions on the structure

and stability of amino-functionalized organic ﬁlms on

silicon substrates by fourier transform infrared spec-

troscopy, ellipsometry, and ﬂuorescence microscopy.

Surf. Sci., 602:3323–3330.

Lenci, S., Tedeschi, L., Domenici, C., Lande, C., Nan-

nini, A., Pennelli, G., Pieri, F., and Severi, S.

(2010). Protein patterning on polycrystalline silicon–

germanium via standard uv lithography for biomems

applications. Materials Science and Engineering C,

doi:10.1016/j.msec.2010.07.002.

Maboudian, R. and Howe, T. (1997). Critical review: ad-

hesion in surface micromechanical structures. J. Vac.

Sci. Technol. B., 15:1–20.

Paci, D., Pieri, F., Toscano, P., and Nannini, A. (2008). A

cmos-compatible, magnetically actuated resonator for

mass sensing applications. Sensors and Actuators B,

129:10–17.

Shen, W., Mathison, L., Petrenko, V., and Chin, B. (2010).

A pulse system for spectrum analysis of magnetoelas-

tic biosensors. Appl. Phys. Lett., 96:163502.

Sone, H., Okano, H., and Hosaka, S. (2004). Picogram

mass sensor using piezoresistive cantilever for biosen-

sor. Jpn. J. Appl. Phys., 43:4663–4666.

Teva, J., Abadala, G., Torresa, F., Verda, J., P

erez-Murano,

F., and Barniola, N. (2006). A femtogram resolution

mass sensor platform, based on soi electrostatically

driven resonant cantilever. part i: Electromechanical

model and parameter extraction. Ultramicroscopy,

106:800–807.

Tilmans, H. (1996). Equivalent circuit representation of

electromechanical transducers: I. lumped-parameter

systems. J. Micromech. Microeng, 6:157–176.

Zuniga, C., Rinaldi, M., Khamis, S., Johnson, A., and Pi-

azza, G. (2009). Nanoenabled microelectromechani-

cal sensor for volatile organic chemical detection. Ap-

plied Physics Letters, 94:223122.

BIODEVICES 2011 - International Conference on Biomedical Electronics and Devices

396