BISTABILITY AND THE COMPLEX DEPLETION PARADOX IN
THE DOUBLE PHOSPHORYLATION-DEPHOSPHORYLATION
CYCLE
Guido Dell’Acqua and Alberto Maria Bersani
Dipartimento di Scienze di Base e Applicate all’Ingegneria, Sapienza Universit`a di Roma
via Antonio Scarpa 16, 00161 Rome, Italy
Keywords:
Michaelis-Menten kinetics, Quasi steady-state approximations, Substrate sequestration.
Abstract:
In this paper we discuss the applicability of the standard quasi steady-state approximation (sQSSA) to complex
enzyme reaction networks, like the ones involved in intracellular signal transduction. In particular we focus on
the dynamics of the intermediate complexes, which in common literature either are ignored or are supposed to
rapidly become negligible in the quasi steady-state phase, differently from what really happens. This brings to
what we call ”complex depletion paradox”, according to which complexes disappear in the conservation laws,
in contrast with the equations of their dynamics. Applying the total quasi steady-state approximation (tQSSA)
to the double phosphorylation-dephosphorylation cycle, we show how to solve the apparent paradox, without
the need of further hypotheses, like, for example, the substrate sequestration.
1 INTRODUCTION -
MICHAELIS-MENTEN
KINETICS AND QUASI
STEADY-STATE
APPROXIMATION
Michelis-Menten kinetics (Henri, 1901a; Henri,
1901b; Michaelis and Menten, 1913; Briggs and Hal-
dane, 1925) represents a fundamental milestone in
biochemistry, as it gives a very good approximation
of the dynamics of the different enzymes involved. Its
formulation considers a reaction where a substrate S
binds an enzyme E reversibly to form a complex C.
The complex can then decay irreversibly to a product
P and the enzyme, which is then free to bind another
molecule of the substrate.
This process is summarized in the scheme
E + S
a
−→
←−
d
C
k
−→ E + P, (1)
where a, d and k are kinetic parameters (supposed
constant) associated with the reaction rates.
The fundamental step is modeling all of the interme-
diate reactions, including binding, dissociation and
release of the product using mass action and conserva-
tion laws. This leads to an ordinary differential equa-
tion (ODE) for each involved complex and substrate,
where the concentration variation for each reactant is
proportional to the reactant concentrations. We refer
to this as the full system.
From now on we will use the same symbols for the
names of the enzymes and their concentrations. For
(1) the equations are
dS
dt
= −a(E
T
−C)S+ dC (2)
dC
dt
= a(E
T
−C)S− (d + k)C . (3)
with initial conditions
S(0) = S
T
, C(0) = 0, (4)
and conservation laws
E +C = E
T
, S+C+ P = S
T
. (5)
The initial conditions give the concentrations of
S and C at the beginning of the reaction, and their
dynamics is described by the ODEs, while E and P
can be deduced from S and C via (5). Here E
T
is
the total enzyme concentration, assumed to be free
at time t = 0. Also the total substrate concentra-
tion, S
T
, is free at t = 0. This is called Michaelis-
Menten (MM) kinetics (Michaelis and Menten, 1913;
55
Dell’Acqua G. and Bersani A..
BISTABILITY AND THE COMPLEX DEPLETION PARADOX IN THE DOUBLE PHOSPHORYLATION-DEPHOSPHORYLATION CYCLE.
DOI: 10.5220/0003169800550065
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2011), pages 55-65
ISBN: 978-989-8425-36-2
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

Briggs and Haldane, 1925; Segel, 1988; Bisswanger,
2002). Let us observe that the system (2–3) admits
only one asymptotic solution. This solution is given
by C = S = 0, so that from (5) we get asymptotically
P = S
T
and E = E
T
. This means that all the substrate
eventually becomes product due to the irreversibility,
while the enzyme eventually is free and the complex
concentration tends to zero.
Assuming that the complex concentration is approxi-
mately constant after a short transient phase leads to
the usual Michaelis-Menten (MM) approximation, or
standard quasi steady-state approximation (sQSSA).
It leads to an ODE for the substrate while the complex
is assumed to be in a quasi-steady state (i.e.,
dC
dt
≈ 0):
dS
dt
≈ −kC ≈ −
V
max
S
K
M
+ S
, S(0) = S
T
, (6)
where
V
max
= kE
T
, K
M
=
d + k
a
. (7)
Segel and Slemrod (Segel and Slemrod, 1989)
showed that a necessary condition for the validity of
the sQSSA approximation is
E
T
≪ K
M
+ S
T
which is valid when the enzyme concentration is
much lower than either the substrate concentration or
the Michaelis constant K
M
(Segel, 1988; Segel and
Slemrod, 1989). This condition is usually fulfilled for
in vitro experiments, but often breaks down in vivo
(Straus and Goldstein, 1943; Sols and Marco, 1970).
However, to simulate physiologically realistic in
vivo scenarios, one faces the problem that the MM
approximation is no longer valid as mentioned above.
Hence, even though the kinetic constants such as K
M
are identical in vivo and in vitro, they need to be im-
plemented in an approximation which is valid for the
system under investigation.
Approximations such as the total QSSA (tQSSA)
(Laidler, 1955; Borghans et al., 1996; Tzafriri,
2003),which is valid for a broader range of parameters
covering both high and low enzyme concentrations,
have been introduced recently. It arises by introduc-
ing the total substrate
¯
S = S +C.
(2)–(3) then become
d
¯
S
dt
= −kC
dC
dt
= a[C
2
− (E
T
+
¯
S+ K
M
)C + E
T
¯
S] . (8)
Assuming that the complex is in a quasi steady-state

dC
dt
= 0

yields the tQSSA
d
¯
S
dt
≈ −kC
−
(
¯
S),
¯
S(0) = S
T
, (9)
where
C
−
(
¯
S) =
(E
T
+ K
M
+
¯
S) −
p
(E
T
+ K
M
+
¯
S)
2
− 4E
T
¯
S
2
(10)
is the only biologically allowable solution of
dC
dt
= 0
in (8).
Tzafriri (Tzafriri, 2003) showed that the tQSSA is
valid whenever
ε
Tz
:=
K
2S
T
E
T
+ K
M
+ S
T
p
(E
T
+ K
M
+ S
T
)
2
− 4E
T
S
T
− 1
!
≪ 1,
(11)
where K =
k
a
, and that this is always roughly valid in
the sense that
ε
Tz
≤
K
4K
M
≤
1
4
. (12)
The parameter K is known as the Van Slyke-Cullen
constant.
Most of current literature uses the sQSSA also to
describe the network of enzyme reactions involved in
the intracellular signal transduction.
However, in vivo the reactions are coupled in
complex networks or cascades of intermediate, sec-
ond messengers with successive reactions, competi-
tion between substrates, feedback loops etc. In some
cases approximations of such scenarios have been car-
ried out within the MM scheme, not only without any
examination of its applicability, but also neglecting
the complexes involved in the reactions (see for ex-
ample (Hatakeyama et al., 2003; Markevich et al.,
2004; Chickarmane et al., 2007)). Other authors (Or-
tega et al., 2006) make use of conservation laws that
account for the presence of the complexes. Neverthe-
less the asymptotic values of the reactants do not yet
correspond to the values obtained integrating numeri-
cally the full systems. In order to explain this appar-
ent incoherence we must underline that the sQSSA,
as every QSSA, represents the system dynamics after
a (in general short) transient phase, during which the
substrates are partially bound and the complexes be-
gin to form. Consequently, since the QSSA is applied
considering the complexes substantially constant, the
total concentration of free and activated substrate(s)
will be considered constant, but its value, due to the
presence of complexes, cannot coincide with the ini-
tial substrate value, when all the complex concentra-
tions were equal to zero. Setting S
T
as initial value
BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms
56

for the total amount of (inactive and activated) sub-
strate concentrations in the sQSSA naturally brings to
wrong conclusions, since the system is forced to ful-
fill a conservation law that implicitly neglects all the
complex concentrations. This is clearly shown in Fig-
ure 6.
In this paper we study the double
phosphorylation-dephosphorylation, on one side
showing that the use of the sQSSA brings to wrong
asymptotic values, on the other showing that the
use of the tQSSA brings to correct predictions for
the asymptotic concentrations of all the reactants,
because the total variables take simultaneously into
account substrates and complexes. In particular,
we show that the sQSSA can predict bistability for
large value ranges, whereas the full system shows
monostability.
2 THE COVALENT
MODIFICATION CYCLE
A case where it is important to consider the contri-
bution from intermediate complexes is the ubiquitous
mechanism of covalent modification, such as the cy-
cle of phosphorylation and subsequent dephosphory-
lation of an enzyme. This reaction is very impor-
tant in every intracellular pathway, because the pro-
cess of phosphorylation and dephosphorylation is one
of the most important to activate and inactivate en-
zymes. The mechanism, which provides the building
blocks of the MAPK cascade, consists of a substrate
S, which can be modified, for example by phosphory-
lation, to the form P. Vice versa, P can be transformed,
e.g. by dephosphorylation, back to S. The scenario
investigated in the ground-breaking work (Goldbeter
and Koshland, 1981) assumes that the enzymesfollow
the Michaelis-Menten reaction mechanism, given by
S+ E
1
a
1
−→
←−
d
1
C
1
k
1
−→ E
1
+ P
P+ E
2
a
2
−→
←−
d
2
C
2
k
2
−→ E
2
+ S
(13)
The reaction is governed by the coupled ODEs
d S
dt
= −a
1
E
1
· S + d
1
C
1
+ k
2
C
2
dC
1
dt
= a
1
E
1
· S − (d
1
+ k
1
)C
1
dC
2
dt
= a
2
E
2
· P− (d
2
+ k
2
)C
2
(14)
with initial conditions
S(0) = S
T
, C
i
(0) = 0, i = 1, 2
and conservation laws
S
T
= S+C
1
+C
2
+ P, (15)
E
i,T
= E
i
+C
i
, i = 1, 2 . (16)
In the MAPK pathway, the upstream kinase (de-
noted MKKK, i.e., MAP kinase kinase kinase; for
example Raf), when activated, phosphorylates the
immediately downstream target, which is also a ki-
nase (MAPKK, i.e., MAP kinase kinase, for example
MEK) successively on two specific sites, eventually
activating it. This last double-phosphorylated kinase
(MAPKK-PP) acts on the MAPK (for example ERK)
through specific phosphorylation events on two dis-
tinct sites. The activated MAPK is then responsible
for further downstream signalling.
The activated cascade is shut down by the reverse
action of specific phosphatases (Camps et al., 2000;
Zhan et al., 2001), whose outcome is the time mod-
ulation of the signal, probably through the regulation
of the active kinase (for example, transient versus sus-
tained activation). Moreover, the phosphatase con-
trols the steady state level of activated MAPK, which,
in turn, controls downstream processes.
The double phosphorylation, as well as double
dephosphorylation of MAPK, was recently modeled
taking into consideration the competition between the
pools of MAPK with different phosphorylation states
(Hatakeyama et al., 2003; Markevich et al., 2004).
We model this process by assuming that competition
holds for both the phosphorylation as well as the de-
phosphorylation processes as in (Hatakeyama et al.,
2003).
In presence of a reaction cycle, it is natural to ex-
pect that the complexesare continuously depleted and
created and that in a stationary state their concentra-
tions cannot tend to zero.
This fact was already observed in (Goldbeter and
Koshland, 1981) in the case of the phosphorylation-
dephosphorylation cycle. Nevertheless most of cur-
rent literature, when applying the sQSSA to complex
schemes, imposes implicitly the depletion of all the
complexes, seriously affecting the conservation laws
and consequently the asymptotic values of the reac-
tant concentrations.
However, as observed in the previous section,
even when the conservation law for substrates takes
into account the complexes, the application of the
sQSSA corresponds to ignore the initial, rapid tran-
sient phase, where complexes begin to be created
and the total amount of free (inactive, monophospho-
rylated and double phosphorylated) substrates is no
more equal to S
T
.
On the other hand the tQSSA cannot produce this
situation, because the substrates and the complexes
BISTABILITY AND THE COMPLEX DEPLETION PARADOX IN THE DOUBLE
PHOSPHORYLATION-DEPHOSPHORYLATION CYCLE
57

formed by them are included in the same (total) vari-
ables and the system cannot distinguish between free
substrates and bound ones. For this reason, differently
from the sQSSA, the tQSSA saves the conservation
laws and produces the same asymptotic values as the
full system.
The most dramatic consequence is that, when ap-
plied to well-known mechanism, like, e.g., the (dou-
ble) phosphorylation-dephosphorylation cycle, or the
MAPK cascade, the sQSSA predicts phenomena
which do not appear when the mechanisms are stud-
ied by means of the full system of equations describ-
ing the systems or by means of the tQSSA.
For example, in (Pedersen et al., 2008) it is
shown that the supposed depletion of the com-
plexes in the sQSSA brings to uncorrect asymptotic
values of the inactive and active substrate in the
Goldbeter-Koshland cycle, as predicted in (Goldbeter
and Koshland, 1981). On the other hand, the tQSSA
reproduces in a very satisfactorily way not only the
asymptotic values but also the dynamics of the reac-
tants.
In (Sabouri-Ghomi et al., 2008) it is shown that,
in several mechanisms, (like, e.g., the antagonistic
toggle switch), the sQSSA can yield bistability even
when the system, described by the full system of
equations, is not bistable.
In (Flach and Schnell, 2006) and (Pedersen et al.,
2008) it is shown that when the system undergoes os-
cillations any QSSA risks to fail, because the cen-
tral hypothesis for the quasi steady-state assumption
is a substantial equilibrium for the complexes, which
cannot be guaranteed in presence of the substrate os-
cillations. Flach and Schnell tested their considera-
tions on the van Slyke-Cullen mechanism (van Slyke
and Cullen, 1914), while Pedersen et al. studied the
MAPK cascade with feedback, as in (Kholodenko,
2000).
In (Ciliberto et al., 2007; Pedersen and Bersani,
2010) it is shown that the tQSSA reproduces zero-
order ultrasensitivity in the Goldbeter-Koshland cy-
cle, according to what was predicted in (Goldbeter
and Koshland, 1981), while the sQSSA, for a wide
range of parameter values, is not able to yield ultra-
sensivity whenever it is expected by the theory.
As already remarked, the main reason for the fail-
ures of the sQSSA lays in the fact that the complexes,
far from asymptotically going to zero, are not ac-
counted in the conservation laws. This implies the
prediction, by the sQSSA, of lower total concentra-
tions than what is expected or experimentally ob-
served. This fact induced some authors (Bluthgen
et al., 2006; Legewie et al., 2007; Xing and Chen,
2008), either to re-discover the sequestration of the
substrates by the kinases or the phosphatates, or to
postulate the existence of some substrate sequestra-
tion mechanisms, by means of competition or inhi-
bition, made by other enzymes. Actually, the use of
the tQSSA not only does not need any additional se-
questration hypothesis, but also correctly accounts for
the exact asymptotic concentration values, of inactive,
active and bound substrates. Let us remark that one
of the main advantages of any QSSA is the simpli-
fication of the mathematical scheme describing the
enzyme reactions, which allows us to capture many
qualitative and quantitative features that could not ob-
served by means of the full system.
In the next section we will compare the applica-
tion of the sQSSA and the tQSSA to the study of
the double phosphorylation-dephosphorylationmech-
anism, showing that, while the latter brings to the
same results as the full system, the former brings to
consistent errors, mainly in the asymptotic concen-
tration values, predicting bistability for large value
ranges, whereas the full system (and the tQSSA) show
monostability.
3 THE EQUATIONS
We want to study the scheme
MAPKK-PP
MAPK
v
1
''
MAPK-P
v
2
((
v
4
gg
MAPK-PP
v
3
hh
MKP3
NN
PP
 
(17)
where the double-phosphorylated kinase (MAPKK-
PP) acts on the MAPK (for example ERK) through
specific phosphorylation events on two distinct sites,
while the phosphatase (MKP3) acts with a reverse ac-
tion on MAPK-PP, inactivating it.
Several authors have modeled this reaction. In
(Ortega et al., 2006) it is supposed that both phospho-
rylation and dephosphorylation happen in only one
step. In (Markevich et al., 2004) the authors describe
the dephosphorylation reaction as a two step mecha-
nism. In (Salazar and Hofer, 2006) both phosphory-
lation and dephosphorylation are assumed to be two
step reactions.
We will focus our analysis on the models de-
scribed in (Ortega et al., 2006) and (Markevich et al.,
2004).
The reaction, as described in (Ortega et al., 2006), can
BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms
58

be summarized as follows
M + E
k
11
−→
←−
k
−11
M − E = C
1
k
12
−→ M
p
+ E
M
p
+ E
k
21
−→
←−
k
−21
M
p
− E = C
2
k
22
−→ M
pp
+ E
(18)
M
pp
+ F
k
31
−→
←−
k
−31
M
pp
− F = C
3
k
32
−→ M
p
+ F
M
p
+ F
k
41
−→
←−
k
−41
M
p
− F = C
4
k
42
−→ M + F
where M, M
p
and M
pp
respectively represent the in-
active, the monophosphorylated and the double phos-
phorylated MAPK, E and F are respectively the ki-
nase MAPKK-PP and the phosphatase MKP3 and C
i
are the intermediate complexes.
Using the law of mass action, the full system of
equations governing the dynamics of the system is
therefore
dM
dt
= −k
11
ME + k
−11
C
1
+ k
42
C
4
dM
p
dt
= −k
21
M
p
E + k
−21
C
2
+ k
−41
C
4
−k
41
M
p
F + k
32
C
3
+ k
12
C
1
dM
pp
dt
= −k
31
M
pp
F + k
−31
C
3
+ k
22
C
2
dC
1
dt
= k
11
ME − (k
−11
+ k
12
)C
1
dC
2
dt
= k
21
M
p
E − (k
−21
+ k
22
)C
2
dC
3
dt
= k
31
M
pp
F − (k
−31
+ k
32
)C
3
dC
4
dt
= k
41
M
p
F − (k
−41
+ k
42
)C
4
(19)
with initial conditions
M(0) = M
T
, M
p
(0) = M
pp
(0) = 0, C
i
(0) = 0,
(20)
where i = 1, . . . , 4 and conservation laws
M + M
p
+ M
pp
+C
1
+C
2
+C
3
+C
4
= M
T
, (21)
E +C
1
+C
2
= E
T
, F +C
3
+C
4
= F
T
. (22)
Setting K
i
=
k
−i1
+ k
i2
k
i1
, i = 1, . . . , 4, the sQSSA im-
plies that
C
1
=
ME
K
1
, C
2
=
M
p
E
K
2
, C
3
=
M
pp
F
K
3
, C
4
=
M
p
F
K
4
(23)
which give
dM
dt
= −
k
12
K
1
ME +
k
42
K
4
M
p
F
dM
p
dt
= −
k
22
K
2
M
p
E −
k
42
K
4
M
p
F +
k
32
K
3
M
pp
F +
k
12
K
1
ME
dM
pp
dt
=
k
22
K
2
M
p
E −
k
32
K
3
M
pp
F
(24)
where
E =
E
T
1+
M
K
1
+
M
p
K
2
, F =
F
T
1+
M
pp
K
3
+
M
p
K
4
and
M(0) = M
T
, M
p
(0) = M
pp
(0) = 0.
Let us observe that, when we apply the sQSSA, we
set all the complexes constant. This means that the
conservation law becomes
M + M
p
+ M
pp
= constant (25)
The constant in (25) is, in general, different from M
T
but the application of both the sQSSA and the con-
servation law since the beginning of the reaction nat-
urally brings to the equality constant = M
T
.
This leads to the complex depletion paradox: the
application of the sQSSA implies that, while the com-
plexes are related to the substrates by the equations
(23), they are implicitly set equal to zero, because of
(25).
The consequences are that the sQSSA predicts
asymptotic values for the different substrate species
which are higher than those ones predicted by the full
system.
Let us introduce the total QSSA (tQSSA) by setting
M = M +C
1
, M
p
= M
p
+C
2
+C
4
, M
pp
= M
pp
+C
3
.
(26)
In terms of these new variables, supposing that the
complexes are in a quasi steady-state, the set of equa-
tions (19) becomes
dM
dt
= k
42
C
4
− k
12
C
1
,
dM
p
dt
= −k
22
C
2
− k
42
C
4
+ k
32
C
3
+ k
12
C
1
,
dM
pp
dt
= −k
32
C
3
+ k
22
C
2
.
(27)
with same initial conditions of (20) and conservation
law
M + M
p
+ M
pp
= M
T
(28)
and where the complexes are given in function of the
total substrates by
BISTABILITY AND THE COMPLEX DEPLETION PARADOX IN THE DOUBLE
PHOSPHORYLATION-DEPHOSPHORYLATION CYCLE
59

(M −C
1
)(E
T
−C
1
−C
2
) − K
1
C
1
= 0
(M
p
−C
2
−C
4
)(E
T
−C
1
−C
2
) − K
2
C
2
= 0
(M
pp
−C
3
)(F
T
−C
3
−C
4
) − K
3
C
3
= 0
(M
p
−C
2
−C
4
)(F
T
−C
3
−C
4
) − K
4
C
4
= 0
(29)
The above system of equations has been obtained us-
ing the QSSA (
dC
i
dt
= 0), (21) and (22) in the last 4
equations of (19).
Let us remark that, in this case, we do not observe
any complex depletion paradox, because the initial
conditions are given on the total substrates, no mat-
ter if the substrates are free or bound. Consequently,
even after the application of the quasi steady-state ap-
proximation, the conservation law is fully respected,
without any additional condition on the complexes.
Thus the tQSSA yields the same asymptotic values
for all the reactants (complexes included) as the full
system.
Similarly, the reaction described in (Markevich et al.,
2004) can be summarized as follows:
M + E
k
1
−→
←−
k
−1
M − E = C
1
k
2
−→ M
p
+ E
M
p
+ E
k
3
−→
←−
k
−3
M
p
− E = C
2
k
4
−→ M
pp
+ E
(30)
M
pp
+ F
h
1
−→
←−
h
−1
C
3
h
2
−→ C
4
h
3
−→
←−
h
−3
M
p
+ F
M
p
+ F
h
4
−→
←−
h
−4
C
5
h
5
−→ C
6
h
6
−→
←−
h
−6
M + F
which can be translated, as before, into differential
equations by the law of mass action:
dM
dt
= −k
1
ME +k
−1
C
1
+ h
6
C
6
− h
−6
MF
dM
p
dt
= −k
3
M
p
E + k
−3
C
2
+ h
3
C
4
− h
−3
M
p
F
−h
4
M
p
F + k
2
C
1
+ h
−4
C
5
dM
pp
dt
= −h
1
M
pp
F + h
−1
C
3
+ k
4
C
2
dC
1
dt
= k
1
ME −(k
−1
+ k
2
)C
1
dC
2
dt
= k
3
M
p
E − (k
−3
+ k
4
)C
2
dC
3
dt
= h
1
M
pp
F − (h
−1
+ h
2
)C
3
dC
4
dt
= h
−3
M
p
F +h
2
C
3
− h
3
C
4
dC
5
dt
= h
4
M
p
F − (h
−4
+ h
5
)C
5
dC
6
dt
= h
5
C
5
+ h
−6
MF −h
6
C
6
(31)
with initial conditions
M(0) = M
T
, M
p
(0) = M
pp
(0) = 0, C
i
(0) = 0,
(32)
where i = 1, . . . , 6 and conservation laws
M + M
p
+ M
pp
+C
1
+C
2
+C
3
+C
4
+C
5
+C
6
= M
T
,
(33)
E +C
1
+C
2
= E
T
, F +C
3
+C
4
+C
5
+C
6
= F
T
.
(34)
Setting
K
i
=
k
−i
+ k
i+1
k
i
, i = 1, 2, H
i
=
h
−i
+ h
i+1
h
i
, i = 1, 4
the sQSSA approximation implies that
C
1
=
ME
K
1
, C
2
=
M
p
E
K
2
, C
3
=
M
pp
F
H
1
,
C
4
=
1
h
3

h
2
M
pp
H
1
+ h
−3
M
p

F , C
5
=
M
p
F
H
4
,
C
6
=
1
h
6

h
5
M
p
H
4
+ h
−6
M

F
which give
dM
dt
= −
k
2
K
1
ME +
h
5
H
4
M
p
F
dM
p
dt
= −
k
4
K
2
M
p
E −
h
5
H
4
M
p
F +
h
2
H
1
M
pp
F +
k
2
K
1
ME
dM
pp
dt
=
k
4
K
2
M
p
E −
h
2
H
1
M
pp
F
(35)
where
E =
E
T
1+
M
K
1
+
M
p
K
2
,
F =
F
T
1+
M
pp
H
1
(1+
h
2
h
3
) + H
5
M
p
+
h
−6
h
6
M
with H
5
=
h
−3
h
3
+
1
H
4
+
h
5
h
6
H
4
and
M(0) = M
T
, M
p
(0) = M
pp
(0) = 0.
Let us introduce again the tQSSA by setting
M = M +C
1
+C
6
, M
p
= M
p
+C
2
+C
4
+C
5
,
M
pp
= M
pp
+C
3
.
In terms of these new variables, supposing that the
complexes are in a quasi steady-state, the set of equa-
tions (31) becomes
dM
dt
= −k
2
C
1
+ h
5
C
5
,
dM
p
dt
= k
2
C
1
− k
4
C
2
+ h
2
C
3
− h
5
C
5
,
dM
pp
dt
= k
4
C
2
− h
2
C
3
.
(36)
BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms
60

with same initial conditions of (20) and conservation
law
M + M
p
+ M
pp
= M
T
(37)
and where the complex are given in function of the
total substrates by
(M −C
1
−C
6
)(E
T
−C
1
−C
2
) − K
1
C
1
= 0
(M
p
−C
2
−C
4
−C
5
)(E
T
−C
1
−C
2
) − K
2
C
2
= 0
(M
pp
−C
3
)(F
T
−C
3
−C
4
−C
5
−C
6
) − H
1
C
3
= 0
h
2
C
3
+ h
−3
(M
p
−C
2
−C
4
−C
5
)(F
T
−C
3
−C
4
−
C
5
−C
6
) − h
3
C
4
= 0
(M
p
−C
2
−C
4
−C
5
)(F
T
−C
3
−C
4
−C
5
−C
6
)−
H
4
C
5
= 0
h
5
C
5
+ h
6
(M −C
1
−C
6
)(F
T
−C
3
−C
4
−C
5
−C
6
) = 0
(38)
As before, the above system of equations has been
obtained using the QSSA (
dC
i
dt
= 0), (33) and (34) in
the last 6 equations of (31).
4 NUMERICAL SIMULATIONS
AND FIGURES
We have numerically integrated (19) and (31), as well
as their M-M approximations (24) and (35), with the
standard MATLAB stiff integrator ODE15S. The set
of kinetic parameters shown in Table (2) was taken
from (Markevich et al., 2004), as well as the value of
M
T
. The set of kinetic parameters shown in Table (1)
is almost the same, except in the two-step dephospho-
rylation phase, where we have eliminated the param-
eters related to the second step. Doing so, we tried
to find the qualitative differences between a one-step
and a two-step dephosphorylation process.
Table 1: Kinetic parameters of reaction (18).
k
11
k
−11
k
12
k
21
0.02 1 0.01 0.032
k
−21
k
22
k
31
k
−31
1 15 0.0045 1
k
32
k
41
k
−41
k
42
0.0092 0.01 1 0.5
The results are shown in Figures 1–7. Note that
the asymptotic values of the tQSSA are not shown
because, as already remarked, the tQSSA gives the
same asymptotic values of the full system. To find
the stationary branches of the three substrate forms
(M, M
p
and M
pp
) we have used an iterative algorithm,
that can be explained briefly as follows. First, when
looking for stationary points, i. e., when we set all the
first members of (19) equal to zero, it is easy to ex-
press all variables in function of the complexesC
1
and
C
2
. Then, we begin the iteration on a stable branch,
Table 2: Kinetic parameters of reaction (30), taken from
(Markevich et al., 2004).
k
1
k
−1
k
2
k
3
0.02 1 0.01 0.032
k
−3
k
4
h
1
h
−1
1 15 0.045 1
h
2
h
3
h
−3
h
4
0.092 1 0.01 0.032
h
−4
h
5
h
6
h
−6
1 0.5 0.086 0.0011
finding the solution of the full system of ODEs via
numerical integration (performed with the standard
MATLAB stiff integrator ODE15S). At the subse-
quent step, to find the solution of the two equations
for C
1
and C
2
on the same stable branch, we use as
starting guess in the MATLAB’s routine FSOLVE the
solution obtained at the previous step, and we repeat
iteratively this procedure. As expected, stability prob-
lems appeared near threshold values, where stable and
unstable stationary branches cross. Fine tuning mech-
anisms of input values of the iterative scheme allowed
us to reconstruct efficiently and satisfactorily all the
three stationary branches.
The computational costs for the simulations and the
iterative algorithm, in terms of CPU time, are in gen-
eral absolutely low, of the order of seconds for the
former, and of few minutes for the latter.
The results show clearly the limits of the sQSSA
when applied to cycles, where the central role of
the intermediates cannot be neglected. Indeed, when
the total amount of enzymes is sufficiently low the
sQSSA approximation shows discrete results (first
two branches on the left of Figures 1–4), while when
the total concentration of enzymes grows the sQSSA
is completely wrong both for the asymptotic values
and, more importantly, for the range of bistability.
Note that for MKP3 = 400, 500 the sQSSA predicts
a wide range of bistability, while the dynamics of the
system is in a monostable regime.
In Figure 5 we show the dynamics of all the sub-
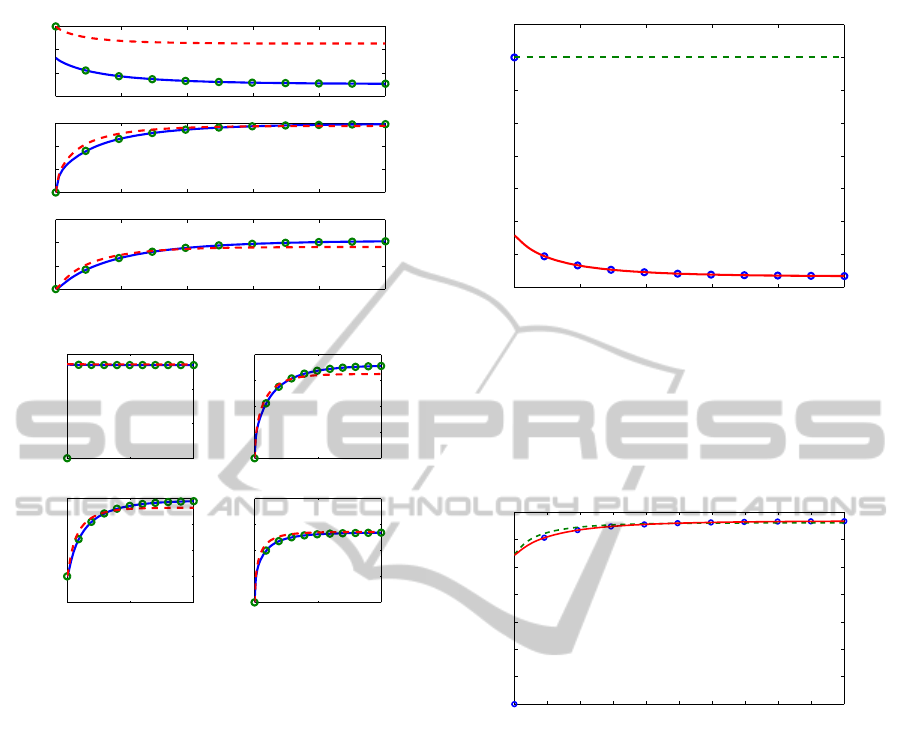
strate and complex concentrations. The sQSSA fails
its prediction of the behavior of M, because the initial
conditions bring to ignore the presence of the com-
plexes, while, as shown in the plot of C
1
, complexes
cannot be neglected, even if the initial kinase and
phosphatase concentrations are much less than M
T
.
In Figures 6–7 we show the meaning of the com-
plex depletion paradox: ignoring the initial, fast tran-
sient phase, the sQSSA imposes as initial condition
for the sum of the substrate concentrations M + M
p
+
M
pp
the value M
T
of the initial concentration of the
unphosphorylated substrate. Actually, even in a fast
transient phase the substrates begin to be bound in
BISTABILITY AND THE COMPLEX DEPLETION PARADOX IN THE DOUBLE
PHOSPHORYLATION-DEPHOSPHORYLATION CYCLE
61

0 100 200 300 400 500 600 700 800
0
50
100
150
200
250
300
350
400
450
500
MAPKK
M
Figure 1: Stationary branches of the inactive MAPKK
(M) in the full system (19) (solid) and in its sQSSA
approximation (24) (dashed), obtained varying the ini-
tial concentration of the kinase MAPKK, for different
values of the initial concentration of the phosphatase:
MKP3=20,50,100,200,300,400,500 (left-right); kinetic pa-
rameters as in Table 1 and M
T
= 500.
0 100 200 300 400 500 600 700 800
0
2
4
6
8
10
12
14
16
18
20
MAPKK
M
p
Figure 2: Stationary branches of the mono-phosphprylated
MAPKK (M
p
) in the full system (19) (solid) and in its
sQSSA approximation (24) (dashed), obtained varying the
initial concentration of the kinase MAPKK, for differ-
ent values of the initial concentration of the phosphatase:
MKP3=20,100,300,500 (left-right); kinetic parameters as in
Table 1 and M
T
= 500.
the complexes and the initial condition for the quasi
steady-state phase should be set less than M
T
. Thus,
using (25), the total contribution of substrates remains
constant, with value M
T
.
Nevertheless, as shown in Figure 7, relations (23)
give at any time a concentration value different from
zero for the total complexes C
1
+ C
2
+ C
3
+ C
4
, in
contrast with the previous figure, where the fact that
M + M
p
+ M
pp
is always equal to M
T
would imply
0 100 200 300 400 500 600 700 800
0
50
100
150
200
250
300
350
400
450
500
MAPKK
M
pp
Figure 3: Stationary branches of the double phosphory-
lated MAPK (M
pp
) in the full system (19) (solid) and in
its sQSSA approximation (24) (dashed), obtained varying
the initial concentration of the kinase MAPKK, for differ-
ent values of the initial concentration of the phosphatase:
MKP3=20,50,100,200,300,400,500 (left-right); kinetic pa-
rameters as in Table 1 and M
T
= 500.
0 50 100 150 200 250 300 350 400
0
50
100
150
200
250
300
350
400
450
500
MAPKK
M
pp
Figure 4: Stationary branches of the double phosphory-
lated MAPK (M
pp
) in the full system (31) (solid) and in
its sQSSA approximation (35) (dashed), obtained varying
the initial concentration of the kinase MAPKK, for differ-
ent values of the initial concentration of the phosphatase:
MKP3=50,100,200,300,400,500 (left-right); kinetic param-
eters as in Table 2 and M
T
= 500.
that C
1
+C
2
+C
3
+C
4
= 0 at any time.
On the other hand, in the tQSSA, considering as
initial condition for the total substrate M(0) = M
T
we
obtain a very good approximation of the true (and in
general unknown) initial condition after the transient
phase, because in this phase we can reasonably sup-
pose that only the binding of M in the complexC
1
has
happened, without affecting the value of M.
BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms
62

0 200 400 600 800 1000
440
460
480
500
M
0 200 400 600 800 1000
0
2
4
6
M
p
0 200 400 600 800 1000
0
5
10
15
time
M
pp
0 500 1000
0
10
20
30
C
1
0 500 1000
0
0.01
0.02
0.03
0.04
C
2
0 500 1000
−2
0
2
4
6
time
C
3
0 500 1000
0
0.2
0.4
0.6
0.8
time
C
4
Figure 5: Dynamics of the system (19) with MAPKK=30,
MKP3=20, kinetics parameters as in Table 1 and M
T
= 500:
full system (circles), tQSSA approximation (solid), sQSSA
approximation (dashed).
5 CONCLUSIONS
Many intracellular reactions are governed by thresh-
old mechanisms. The wrong determination of the
asymptotic reactant concentrations can heavily affect
the mathematical model of the system and its predic-
tions. Though the sQSSA represents a very important
tool for the qualitative and quantitative study of sin-
gle enzyme–substrate reactions, it has shown to be in
general inadequate, for several reasons, when applied
to complex reaction networks, like those ones occur-
ring inside the cell.
In this paper we show that, in the case of the
phosphorylation-dephosphorylation cycle, the appli-
cation of the tQSSA or, better, of the full system of
equations is in general much more appropriate.
One of the main advantages of the sQSSA is the
simplification of the mathematical scheme describ-
ing the enzyme reactions, which allows us to capture
many qualitative and quantitative features that could
not observed by means of the full system. Again, as
0 200 400 600 800 1000
465
470
475
480
485
490
495
500
505
time
Figure 6: Dynamics of M + M
p
+ M
pp
in the reaction (18):
full system (circles), tQSSA approximation (solid), sQSSA
approximation (dotted). Here MAPKK=30, MKP3=20, ki-
netic parameters as in Table 1 and M
T
= 500. Differently
from the full system and the tQSSA, the sQSSA predicts at
any time a constant value M
T
for M+M
p
+M
pp
that would
imply C
1
+C
2
+C
3
+C
4
= 0.
0 100 200 300 400 500 600 700 800 900 1000
0
5
10
15
20
25
30
35
time
Figure 7: Dynamics of C
1
+ C
2
+C
3
+C
4
in the reaction
(18): full system (circles), tQSSA approximation (solid),
sQSSA approximation (dashed). Here MAPKK=30,
MKP3=20, kinetics parameters as in Table 1 and M
T
= 500.
In contrast with the previous figure, the sQSSA predicts at
any time a value of C
1
+C
2
+C
3
+C
4
different from zero.
shown in this paper, the application of the tQSSA
brings to predictions that are much more accurate
than the sQSSA ones, quantitatively and qualitatively.
Thus, the use of the total substrates shows to be much
more than a mere variable change, bringing to a cor-
rect explanation and prediction of the sequestration
mechanism, which is not allowed by the sQSSA.
Let us also remark that, as shown in (Pedersen
et al., 2008), in presence of mechanisms, like feed-
backs, generating oscillations, any QSSA is inad-
equate to approximate the full system, since sub-
strate oscillations imply kinase and phosphatase os-
cillations, which are in contrast with the main quasi
steady-state assumption. In this cases, in order to
obtain realistic predictions, the reactions can be de-
scribed only by the full system, though it contains a
BISTABILITY AND THE COMPLEX DEPLETION PARADOX IN THE DOUBLE
PHOSPHORYLATION-DEPHOSPHORYLATION CYCLE
63

much greater number of equations and variables.
Our aim is to extend our investigations to more
complex reactions, governing the cell function-
ing. In fact, it is well known that the mathe-
matical description of the double phosphorylation–
dephosphorylation mechanism is a common feature
not only of the MAPK but of any reaction involving a
double-step activation and the corresponding double-
step deactivation. Even if we expect, in general, much
more involved phenomena, we think that our mathe-
matical tools will be able to model, explain and pre-
dict their main characteristics.
The results that we present in this paper do need,
of course, a validation through experimental data. For
this purpose, we have got off the ground a collabora-
tion with personnel from ISMAC–CNR, the Institute
for Macromolecular studies (Genova,Italy), in order
to test our predictions.
REFERENCES
Bisswanger, H. (2002). Enzyme Kinetics. Principles and
Methods. Wiley-VCH.
Bluthgen, N., Bruggeman, F. J., Legewie, S., Herzel, H.,
Westerhoff, H. V., and Kholodenko, B. N. (2006). Ef-
fects of sequestration on signal transduction cascades.
FEBS J., 273:895–906.
Borghans, J., de Boer, R., and Segel, L. (1996). Extend-
ing the quasi-steady state approximation by changing
variables. Bull. Math. Biol., 58:43–63.
Briggs, G. E. and Haldane, J. B. S. (1925). A note on the
kinetics of enzyme action. Biochem. J., 19:338–339.
Camps, M., Nichols, A., and Arkinstall, S. (2000). Dual
specificity phosphatases: a gene family for control of
map kinase function. FASEB J., 14:6–16.
Chickarmane, V., Kholodenko, B. N., and Sauro, H. M.
(2007). Oscillatory dynamics arising from competi-
tive inhibition and multisite phosphorylation. J. Theor.
Biol., 244:68–76.
Ciliberto, A., Capuani, F., and Tyson, J. J. (2007). Model-
ing networks of coupled anzymatic reactions using the
total quasi-steady state approximation. PLoS Comput.
Biol., 3:463–472.
Flach, E. H. and Schnell, S. (2006). Use and abuse of the
quasi-steady-state approximation. IEE Proceed. Syst.
Biol., 153:187–191.
Goldbeter, A. and Koshland, D. E. (1981). An amplified
sensitivity arising from covalent modification in bio-
logical system. Proc Natl Acad Sci, 78:6840–6844.
Hatakeyama, M., Kimura, S., Naka, T., Kawasaki, T., Yu-
moto, N., Ichikawa, M., Kim, J. H., Saito, K., Saeki,
K. M., Shirouzu, M., Yokoyama, S., and Konagaya, A.
(2003). A computational model on the modulation of
mitogen-activated protein kinase (mapk) and akt path-
ways in heregulin-induced erbb signalling. Biochem.
J., 373:451–463.
Henri, V. (1901a). Recherches sur la loi de l’action de la
sucrase. C. R. Hebd. Acad. Sci., 133:891–899.
Henri, V. (1901b).
¨
Uber das gesetz der wirkung des in-
vertins. Z. Phys. Chem., 39:194–216.
Kholodenko, B. N. (2000). Negative feedback and ultra-
sensitivity can bring about oscillations in the mitogen-
activated protein kinase cascades. Eur. J. Biochem.,
267:1583–1588.
Laidler, K. J. (1955). Theory of the transient phase in kinet-
ics, with special reference to enzyme systems. Can. J.
Chem., 33:1614–1624.
Legewie, S., Schoeberl, B., N., B., and Herzel, H. (2007).
Competing docking interactions can bring about bista-
bility in the mapk cascade. Biophys. J., 93:2279–
2288.
Markevich, N. I., Hoek, J. B., and B.N., K. (2004). Sig-
naling switches and bistability arising from multisite
phosphorylation in protein kinase cascades. J. Cell
Biol., 164:353–359.
Michaelis, L. and Menten, M. L. (1913). Die kinetik der
invertinwirkung. Biochem. Z., 49:333–339.
Ortega, F., Garces, J. L., Mas, F., Kholodenko, B. N., and
Cascante, M. (2006). Bistability from double phos-
phorylation in signal transduction. kinetic and struc-
tural requirements. FEBS J., 273:3915–3926.
Pedersen, M. and Bersani, A. M. (2010). The total quasi-
steady state approximation simplifies theoretical anal-
ysis at non-negligible enzyme concentrations: Pseudo
first-order kinetics and the loss of zero-order ultrasen-
sitivity. J. Math. Biol., 60:267–283.
Pedersen, M. G., Bersani, A. M., and Bersani, E. (2008).
Steady-state approximations in intracellular signal
transduction – a word of caution. J. Math. Chem.,
43:1318–1344.
Sabouri-Ghomi, M., Ciliberto, A., Kar, S., Novak, B., and
Tyson, J. J. (2008). Antagonism and bistability in pro-
tein interaction networks. J. Theor. Biol., 250:209–
218.
Salazar, C. and Hofer, T. (2006). Kinetic models of phos-
phorylation cycles: A systematic approach using the
rapid equilibrium approximation for protein-protein
interactions. Biosystems, 83:195–206.
Segel, L. (1988). On the validity of the steady state assump-
tion of enzyme kinetics. Bull. Math. Biol., 50:579–
593.
Segel, L. A. and Slemrod, M. (1989). The quasi steady-state
assumption: a case study in perturbation. Siam Rev.,
31:446–477.
Sols, A. and Marco, R. (1970). Concentrations of metabo-
lites and binding sites, implications in metabolic reg-
ulation. Curr. Top. Cell. Regul., 2:227–273.
Straus, O. H. and Goldstein, A. (1943). Zone behavior of
enzymes. J. Gen. Physiol., 26:559–585.
Tzafriri, A. R. (2003). Michaelis-Menten kinetics at high
enzyme concentrations. Bull. Math. Biol., 65:1111–
1129.
BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms
64

van Slyke, D. D. and Cullen, G. E. (1914). The mode of
action of urease and of enzymes in general. J. Biol.
Chem., 19:141–180.
Xing, J. and Chen, J. (2008). The Goldbeter-Koshland
switch in the first-order region and its response to dy-
namic disorder. PLOS ONE, 3:e2140.
Zhan, X. L., Wishart, M., and L., G. K. (2001). Nonrecep-
tor tyrosine phosphatases in cellular signaling: regula-
tion of mitogen-activated protein kinases. Chem. Rev.,
101:2477–96.
BISTABILITY AND THE COMPLEX DEPLETION PARADOX IN THE DOUBLE
PHOSPHORYLATION-DEPHOSPHORYLATION CYCLE
65