A HIGH ACCURACY CT BASED FEM MODEL

OF THE LUMBAR SPINE TO DETERMINE

ITS BIOMECHANICAL RESPONSE

A. Tsouknidas

Laboratory for Machine Tools and Manufacturing Engineering, Mechanical Engineering Department

Aristoteles University of Thessaloniki, Thessaloniki, Greece

N. Michailidis, S. Savvakis

Physical Metallurgy Laboratory, Mechanical Engineering Department, Aristoteles University of Thessaloniki

Thessaloniki, Greece

K. Anagnostidis

Orthopaedic Department ”Papageorgiou” General Hospital, Aristoteles University of Thessaloniki

Thessaloniki, Greece

K.-D. Bouzakis

Laboratory for Machine Tools and Manufacturing Engineering, Mechanical Engineering Department

Aristoteles University of Thessaloniki, Thessaloniki, Greece

G. Kapetanos

Orthopaedic Department ”Papageorgiou” General Hospital, Aristoteles University of Thessaloniki

Thessaloniki, Greece

Keywords: Computer Tomography, Lumbar Spine, High Accuracy FEM Model, Biomechanical Response.

Abstract: The lumbar spine is origin of the most frequent complains among all human body parts, since almost 80%

of the population will at some point in life exhibit back related pathologies which in their majority will not

require invasive surgery. Regardless the cause or the development of the problem, the in-depth investigation

of its cause is of the upmost importance during treatment or preoperative evaluation. In this context a model

of the L1-L5 vertebra, capable of accurately assessing the biomechanical response of the lumbar spine

derived from human activity as well as externally induced loads, would be an effective tool during the

examination of normal or clinical conditions. This study presents a CT based FEM model of the lumbar

spine taking into account all function related boundary conditions such as mechanical property anisotropy,

ligaments, contact elements mesh size etc. The developed model is capable of comparing the mechanical

response of a healthy lumbar spine to any given pathology, which can be easily introduced into the model,

thus providing valuable insight on the stress development within the model and predict critical movements

and loads of potential patients.

1 INTRODUCTION

Three dimensional finite element models

representing functional parts of the spine have been

repeatedly introduced over the last years in order to

simulate the biomechanical response of spinal units

(Little et al, 2010, Ezquerro et al, 2004, Wang et al,

2006) or investigate trauma related surgical

treatment (Polikeit et al, 2003, Ashish and Pramod

2009).

Several methods used to obtain the geometrical

characteristics of the investigated set of vertebra

have also been introduced. Even though touch probe

222

Tsouknidas A., Michailidis N., Savvakis S., Anagnostidis K., Bouzakis K. and Kapetanos G..

A HIGH ACCURACY CT BASED FEM MODEL OF THE LUMBAR SPINE TO DETERMINE ITS BIOMECHANICAL RESPONSE .

DOI: 10.5220/0003172102220227

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2011), pages 222-227

ISBN: 978-989-8425-36-2

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

digitizers (Lee et al, 2002) and laser scanners (Heuer

et al, 2007) are able to provide high accuracy

measurements, thus leading to an accurate

representation of the spine, non intrusive methods

such as CT (Kinder et al, 2009) or nuclear magnetic

resonance (NMR) (Pfirrmann, et al, 2001) ease the

extraction of a patients’ examined areas geometry

while comparing favorably in terms of data

processing and inherent defect determination.

Recent studies have used combinations of the

above techniques to simulate parts of the human

spine ranging from a set of vertebra (Lodygowski et

al, 2005) up to several parts of the spine (Guan et al,

2006). Nevertheless, a high accuracy CT based

model of the lumbar spine with regard to specific

material related properties (directional anisotropy of

the bone, etc.) and all relating connective tissue

(unequal properties distribution among annulus

fibrosus layers, ligaments, contact areas etc.) has to

the best of our knowledge, yet to be introduced. This

exact task is the aim of the present investigation.

2 ANALYTICAL MODEL

2.1 Volume Reconstruction

During the reconstruction of the lumbar spine (L1-

L5) CT were the imaging modality of choice due to

their ability to demonstrate high inherent image

contrast between bone and soft tissue. This enables

relatively unhindered segmentation of the bone from

soft tissue, allowing the generation of a

geometrically accurate volumetric data set of the

patients lumbar spine. The basic concept is to

overlay CT scan slices which represent the outline of

each vertebra with respect to the angulations of the

spines axis (Blankevoort et al., 2008; Beimersade et

al., 2008; Kobayashi et al., 2009). During the

present investigation apatients lumbar spine was

scanned in its entirety from below the lower

boundaries of L1 to the upper limit of L5 ensuring

the full 3D visual representation of the examined

area.

Data acquisition was in accordance to DICOM

(Digital Imaging and Communications in Medicine)

and interpolation of the CT information ensured an

isotropic data set. Although this process did not

result in higher resolution of the reconstructed set of

vertebra, it lead to smoother representation allowing

the distinct removal of the remaining soft tissue in

close proximity to the bone.

After the representation of the surfaces the

resulting volumes were generated considering an

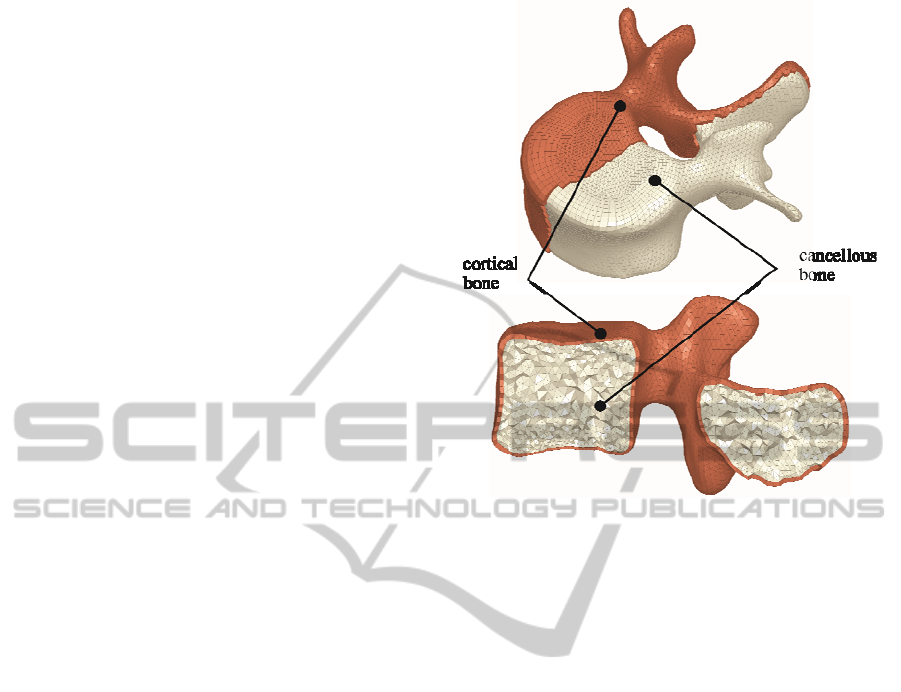
Figure 1: Resulting mesh of of the L5 vertebra.

outer cortex for each vertebra corresponding to the

cortical bone with a varying thickness of 0.5-1mm

depending on the longitudal slice of volume in the

spines axial direction. The remaining volume of

each vertebra was considered as cancellous bone and

described as such in the way illustrated in Figure 1.

Unlike the aforementioned procedure, the

intervertebral discs of the lumbar spine were reverse

engineered based on the superior and inferior surface

of the connecting vertebral bodies. This method

compares favorably to the regeneration of the discs

based on CT measurements due to the fact that their

volume is characterized by severely altering density

and the inhomogeneous tissue does not facilitate

precise segmentation by imaging techniques. The

geometric characteristics of the intervertebral discs

were designed based on the existing spinal bone

tissue while anatomic data like the inner nucleus

pulposus and the surrounding outer annulus were

considered. The resulting superior and inferior

meshed geometry of every intervertebral disc (see

Figure 2) consists of six spline based layers,

proportional concentric to the outer contour of the

disc, covering a total of 65% of the discs superior

and inferior surface.

2.2 FEM Model

During the meshing of the intervertebral discs,

quadric elements were employed for the annulus

A HIGH ACCURACY CT BASED FEM MODEL OF THE LUMBAR SPINE TO DETERMINE ITS BIOMECHANICAL

RESPONSE

223

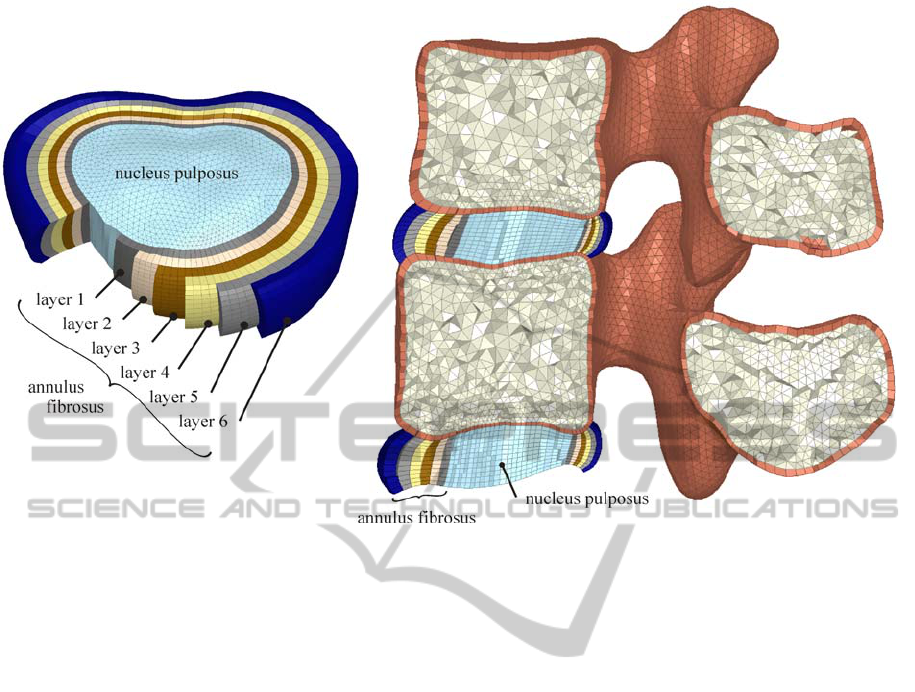
Figure 2: Intervertebral disc reconstruction with nucleus pulposus and the surrounding annulus ground substance.

ground substance in order to facilitate the

implementation of the annulus fibrosus in form of

cable elements positioned crosswise within the

tetrahedron structure ensuring accurate simulation of

their biomechanical response.

The remaining model, nucleus pulposus and

vertebrae, composes of tetra elements (pyramides)

and the unhindered connection at the models contact

areas (quadric- tetra elements interface) was ensured

through the diametrical incision of two triangles in

every rectangle, maintaining the same nodes

throughout the intervertebral disc surface and the

vicinical vertebrae. This approach obviated the

usage of contact elements thus reducing the

processing time of the FEM model.

The mechanical properties of cortical and

cancellous bone were considered as anisotropic (Lu

and Hutton, 1996, Smit et al, 1997) and are

presented in Table 1 along with the strength

characteristics of the nucleus pulposus and the of the

annulus ground substance intervertebral discs.

Among the most important characteristics of the

FEM model was the incorporation of a set of cable

elements, adding valuable mechanical characteristics

to the simulation. The annulus fibrosus was

considered to exhibit varying young modulus for

each set of layer in the radial direction of the

annulus (as presented in Figure 2) in order to reflect

the unequal distribution of this structures properties.

Next to these several other cable elements were

employed representing the remaining connective

tissue between each set of vertebrae, thus ensuring

the precise transition of forces among the vertebra

and simulating the accurate biomechanical response

of the lumbar spine.

Figure 3a demonstrates all aforementioned

connections (ligaments, contact elements and

annulus fibrosus) used as input to the FEM software

(Ansys 12.1 Academic license) as well as a

simplified model (Figure 3b) illustrating only the

cable and contact elements considered during the

simulation.

The mechanical properties as well as the cross

sectional area of each cable element used within the

model (Shirazi-ald et al, 1984, Smit et al, 1997, Lu

and Hutton, 1996) are presented in Table 2. All

cable elements were simulated with Ansys link 10

elements which are capable of receiving only tension

loads resembling the ligaments in a rather accurate

way.

The meshing of the spine segment was

conducted in ANSA of BETA CAE Systems in

order to ensure all above mentioned characteristics

leading to a realistic and isotropic stress transition

within the considered bone and intervertebral disc.

The resulting max. and min. element size as well as

the number of elements for each set of material

considered, are demonstrated in Table 3.

BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms

224

Table 1: Material properties and element specifications of cortical and cancellous bone as well as nucleus pulposus and

annulus ground substance.

Material type Young modulus [Mpa] Poisson ratio Element type used

Cortical bone E

= 11.300 v

= 0,484 solid 185

= 11.300 v

= 0,203

22.000 v

= 0,203

= 3.800

= 5.400

Cancellous bone E

= 140 v

= 0,45 solid 95

= 140 v

= 0,315

= 200 v

= 0,315

= 48,3

Nucleus pulposus 0,2 v = 0.4999 solid 185

Annulus ground substance 4,2 v = 0.45 solid 185

Figure 3: a) Set of two vertebrae (L4 and L5), intervertebral disc and ligaments b) simplified model without bone and tissue

presenting only ligaments and contact elements.

Table 2: Mechanical properties of ligaments, contact elements and annulus fibrosus layers.

Cable element type Young modulus [Mpa] Poisson ratio Cross-sectional area [mm

]

Lig. long. anterius 20 0,3 38

Lig. long. Posterius 70 0,3 20

Lig. flava 50 0,3 60

Lig. intertransversia 50 0,3 10

Lig. interspinalia 28 0,3 35,5

Lig. supraspinalia 28 0,3 35,5

Lig. capsulae 20 0,3 40

Annulus fibrosus layer 1 550 0,45 0,7

Annulus fibrosus layer 2 495 0,45 0,63

Annulus fibrosus layer 3 440 0,45 0,55

Annulus fibrosus layer 4 420 0,45 0,49

Annulus fibrosus layer 5 385 0,45 0,41

Annulus fibrosus layer 6

360

0,45

0,3

A HIGH ACCURACY CT BASED FEM MODEL OF THE LUMBAR SPINE TO DETERMINE ITS BIOMECHANICAL

RESPONSE

225

Table 3: Mesh related figures of the lumbar spine model.

Material

type

no. of

Elements

max size

Element

min size

Element

Cortical

bone

87.521 1,78 mm 0,08 mm

Cancellous

bone

712.361 3,04 mm 0,97 mm

Nucleus

pulposus

317.251 2,27 mm 0,72 mm

Annulus 298.657 3,71 mm 1,87 mm

3 RESULTS

The validation of the model was based on torsion,

extension, flextion, left and right bending

simulations to determine the resulting inclination of

spine segments under specific loads and compare

those to experimental values found in literature

(Panjabi et al, 1994). Figure 4 demonstrates the

developing stress distribution of the examined set

and intervertebral disc for a 10Nm flexion moment.

Figure 4: Calculated stress distribution on a set of L2-L3

vertebrae subjected to extension.

Figure 5 exhibits that the load induced response of

the vertebra is almost identical to its experimentally

determined one.

Figure 5: Calculated and experimental load-inclination

diagram.

4 CONCLUSIONS

The introduced model facilitates the evaluation of

induced loads on the lumbar spine. Pathological

defects, trauma as well as therapy oriented

intervention can be assessed prior to the actual

practice on the patient. This model may also be a

valuable tool in preoperative evaluation of the

biomechanical response of the system to a function

specific implant.

ACKNOWLEDGEMENTS

The authors would like to thank BETA CAE

Systems SA for providing them with the CAE pre-

processor ANSA, used during surface and volume

generation and meshing of the introduced model.

REFERENCES

Little, J. P., Pearcy, M. J., Tevelen, G., Evans, J. H.,

Pettet, G., Adam, C. J., 2010, The mechanical

response of the ovine lumbar anulus fibrosus to

uniaxial, biaxial and shear loads, Journal of the

Mechanical Behavior of Biomedical Materials, 3, 146-157

Ezquerro, F., Simón, A., Prado, M., Pérez, A., 2004,

Combination of finite element modeling and

optimization for the study of lumbar spine

biomechanics considering the 3D thorax–pelvis

orientation, Medical Engineering & Physics, 26(1),

11-22

Wang, J. P., Zhong, Z C., Cheng, C. K., Chen, C. S., Yu,

C. H., Chang, T.K., Wei, S.H., 2006, Finite element

analysis of the spondylolysis in lumbar spine., Biomed

Mater Eng.16(5), 301-308.

Polikeit, A., Ferguson, S.J., Nolte, L.P., Orr, T.E., 2003,

Factors influencing stresses in the lumbar spine after

the insertion of intervertebral cages: finite element

analysis. Eur Spine J., 12(4):413-20

BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms

226

Ashish, D., Pramod, P,, 2009, Development of Computer

Aided 3D Model From Computed Tomography

Images and its Finite Element Analysis for Lumbar

Interbody Fusion with Instrumentation, International

Journal of CAD/CAM 9(1) 121-128

Lee, K. K. Teo, E. C. Qiu, T. X. Ng, H. W. and Yang, K.,

2003, Finite element modeling of L2-L3 using

digitizer,” Int. J. Computer Application Technology

(IJCAT) (Special issue on Biomedical Engineering

and I.T.) 20 1-9

Heuer, F., Schmidt, H., Claes, L., Wilke, H. J., 2008, A

new laser scanning technique for imaging

intervertebral disc displacement and its application to

modeling nucleotomy, Arthroscopy: The Journal of

Arthroscopic and Related Surgery 23(3) 260-269

Klinder, T., Ostermann, J., Ehm, M., Franz, A., Kneser,

R., Lorenz, C., 2009, Automated model-based vertebra

detection, identification, and segmentation in CT

images, Medical Image Analysis 13, 471–482

Pfirrmann, C., Metzdorf, A., Zanetti, M., Hodler, J., Boos,

N., 2001, Magnetic Resonance Classification of

Lumbar Intervertebral Disc Degeneration, SPINE

26(17), 1873–1878

Lodygowsky, T., Kakol, W., ierszycki, M., 2005, Three-

dimensional nonlinear finite element model of the

human lumbar spine segment, Acta of Bioengineering

and Biomechanics 7(2)

Guan, Y., Yoganandan, N., Zhang, J., Pintar, F., Cusick,

J., Wolfla, C., Maiman, D., 2006, Validation of a

clinical finite element model of the human

lumbosacral spine, Med Bio Eng Comput 44, 633–641

Blankevoort, L., Beimers, L., Jonges, R., Valstar, E.R.,

Tuijthof, G.J.M., 2008. The accuracy of a CT-based

bone segmentation technique for measuring the range

of motion of the joints in the ankle. J. Foot Ankle Res.

1, O34

Beimersade, L., Tuijthofde, G.J.M., Blankevoortde, L.

Jonges. R., Maas, M., Van Dijk, C.N., 2008. In-vivo

range of motion of the subtalar joint using computed

tomography, J. Biomech. 41, 1390-1397

Kobayashi, K., Odagawa, K., Sakamoto, M., Tanabe, Y.,

2009. Accuracy of Single Plane X-Ray Image-Based

Technique for Assessment of Knee Kinematics,

Journal of Biomechanical Science and Engineering 4,

192-200

Lu, Y.M, Hutton, W.C, Gharpuray, V.M., 1996, Do

bending, twisting and diurnal fluid change in the disc

affect the propensity to prolapse? A viscoelastic finite

element model. Spine, 21,2570-2579.

Smit, T. H., Odgaard, A., Schneider, E., 1997, Structure

and function of vertebral trabecular bone. Spine

15;22(24), 2823-2833.

Shirazi-Adl, S.A., Shrivastava, S.C., Ahmed, A.M., 1984,

Stress analysis of the lumbar disc-body unit in

compression. A three-dimensional nonlinear finite

element study. Spine 9(2),120-34

A HIGH ACCURACY CT BASED FEM MODEL OF THE LUMBAR SPINE TO DETERMINE ITS BIOMECHANICAL

RESPONSE

227