
OPTICAL FLOW BY MULTI-SCALE ANNOTATED KEYPOINTS
A Biological Approach
Miguel Farrajota, J. M. F. Rodrigues and J. M. H. du Buf
Vision Laboratory, Institute for Systems and Robotics (ISR)
University of the Algarve (ISE and FCT), 8005-139 Faro, Portugal
K
eywords:
Optical flow, Multi-scale, Keypoint classification, Visual cortex, Segregation, Tracking.
Abstract:
Optical flowis the pattern of apparent motion of objects in a visual scene and the relative motion, or egomotion,
of the observer in the scene. In this paper we present a new cortical model for optical flow. This model is based
on simple, complex and end-stopped cells. Responses of end-stopped cells serve to detect keypoints and those
of simple cells are used to detect orientations of underlying structures and to classify the junction type. By
combining a hierarchical, multi-scale tree structure and saliency maps, moving objects can be segregated, their
movement can be obtained, and they can be tracked over time. We also show that optical flow at coarse scales
suffices to determine egomotion. The model is discussed in the context of an integrated cortical architecture
which includes disparity in stereo vision.
1 INTRODUCTION
Optical flow, also called optic flow, is the motion pat-
tern caused by moving objects in a visual scene. It
can be described by motion or displacement vectors
of entire objects or parts of them between successive
time frames. In the case of egomotion, i.e., the eye
of a moving person or a moving camera, the relative
motion between observer and scene also contributes.
Experiments have strengthened the arguments that
neurons in a specialised region of the cerebral cortex
play a major role in flow analysis (Wurtz, 1998), that
neuronal responses to flow are shaped by visual strate-
gies for steering (William and Charles, 2008), and
that flow processing has an important role in the de-
tection and estimation of scene-relative object move-
ments during egomotion (Warren and Rushton, 2009).
For the latter, the brain identifies and globally dis-
counts (i.e., subtracts) optical flow patterns across the
visual scene, a process called flow parsing.
(Morrone et al., 2000) demonstrated that neurons
in area V5/MT (medial temporal) respond selectively
to components of optical flow, such as circular and
radial motion. (Smith et al., 2006) showed that neu-
rons in area MST (middle superior temporal) seem to
be more selective to complex movements than those
in area MT, the latter being more devoted to simple
movements, although both areas respond to all mo-
tion stimuli but with different activation patterns. Al-
though many cells may respond to more than one type
of motion stimulus, individual cells show different di-
rection selectivities (Duffy and Wurtz, 1991). In ad-
dition, cells in area MST were reported to be selective
for rotation and expansion (Orban et al., 1992), hav-
ing larger receptive fields and less precise retinotopic
mapping than those in area MT. Therefore, MST cells
conveymore global information about a scene’s struc-
ture and motions (Smith et al., 2006).
An essential function of visual processing is to
establish the position of the body in space and, in
concert with the other sensory systems, to monitor
its movements: egomotion through optical flow (Wall
and Smith, 2008). For example, forward motion gen-
erates an expanding flow pattern on the retinae and,
with eyes fixated centrally, the heading direction cor-
responds to the centre of expansion. Area MST being
sensitive to more global optical flow patterns, it has
been suggested that MST has a central role in guid-
ing heading in macaques. The same authors identi-
fied two areas of the human brain which represent vi-
sual cues to egomotion more directly than does area
MST. One is the putative area VIP in the anterior part
of the intraparietal sulcus. The other is a new visual
area coined cingulate sulcus visual area (CSv). In
contrast to these new areas, areas V1 to V4 and MT
respond about equally to stimuli mimicking arbitrary
motion and egomotion, whereas area MST has inter-
mediate properties, responding well to various motion
307
Farrajota M., M. F. Rodrigues J. and M. H. du Buf J..
OPTICAL FLOW BY MULTI-SCALE ANNOTATED KEYPOINTS - A Biological Approach.
DOI: 10.5220/0003172403070315
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2011), pages 307-315
ISBN: 978-989-8425-35-5
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

stimuli but with a modest preference for egomotion-
compatible stimuli.
Apart from motion processing, we know that the
visual cortex detects and recognises objects by means
of the ventral “what” and dorsal “where” subsystems.
Both bottom-up (visual input code) and top-down(ex-
pected object and position) data streams are necessary
for obtaining size, rotation and translation invariance,
assuming that object templates are normalised in vi-
sual memory.
Recently we presented cortical models based on
multi-scale line/edge and keypoint representations
(Rodrigues and du Buf, 2006; Rodrigues and du Buf,
2009b). These representations, all based on responses
of simple, complex and end-stopped cells in V1, can
be integrated for different processes: visual recon-
struction or brightness perception, focus-of-attention
(FoA), object segregation and categorisation, and ob-
ject and face recognition. The integration of FoA, re-
gion segregation and object categorisation is impor-
tant for developing fast gist vision, i.e., which types
of objects are about where in a scene.
Optical flow, as for disparity in stereo vision, com-
plements colour and texture in object segregation,
possibly in, but not necessarily limited to, the dorsal
“where” pathway where keypoints may play a major
role in FoA (Rodrigues and du Buf, 2006). In this pa-
per we present a new model for cortical optical flow
which is based on annotated (classified) multi-scale
keypoints. We show that the information can be used
for egomotion and for object segregation and track-
ing.
In Section 2 we present multi-scale keypoint de-
tection and annotation, in Section 3 optical flow de-
tection, in Section 4 object tracking using optical flow
information, and we conclude with a final discussion
and lines for future work in Section 5.
2 MULTI-SCALE KEYPOINT
ANNOTATION
Keypoints are based on end-stopped cells (Rodrigues
and du Buf, 2006). They provide important informa-
tion because they code local image complexity. More-
over, since keypoints are caused by line and edge jun-
tions, detected keypoints can be classified by the un-
derlying vertex structure, such as K, L, T, + etc. This
is very useful for most if not all matching problems:
object recognition, stereo disparity and optical flow.
In this section we describe the multi-scale keypoint
detection and annotation processes.
2.1 Keypoint Detection
Gabor quadrature filters provide a model of cortical
simple cells (Rodrigues and du Buf, 2006). In the
spatial domain (x,y) they consist of a real cosine and
an imaginary sine, both with a Gaussian envelope.
Responses of even and odd simple cells, which cor-
respond to real and imaginary parts of a Gabor fil-
ter, are obtained by convolving the input image with
the filter kernel, and are denoted by R
E
s,i
(x,y) and
R
O
s,i
(x,y), s being the scale, i the orientation (θ
i
=
iπ/N
θ
) and N
θ
the number of orientations (here 8)
with i = [0,N
θ
− 1]. Responses of complex cells are
then modelled by the modulus
C
s,i
(x,y) = [{R
E
s,i
(x,y)}
2
+ {R
O
s,i
(x,y)}
2
]
1/2
.
There are two types of end-stopped cells, single and
double. These are applied to C
s,i
and are combined
with tangential and radial inhibition schemes in or-
der to obtain precise keypoint maps K
s
(x,y). For a
detailed explanation with illustrations see (Rodrigues
and du Buf, 2006). Below, the scale of analysis will
be given by λ expressed in pixels, where λ = 1 corre-
sponds to 1 pixel.
Figure 1 (top-left) shows a scene with, on the sec-
ond row from top, keypoints detected (diamond sym-
bols) at two scales λ = 6 (left) and 27 (right). At
top-right it shows one quadrant of a test image with
a black square against a homogeneous background
(top-left) and a noisy background (top-right), both
with a correctly detected keypoint at the junction. All
other images show annotated keypoints; see below.
2.2 Keypoint Annotation
In order to classify any detected keypoint, the re-
sponses of simple cells R
E
s,i
and R
O
s,i
are analysed, but
now using N
φ
= 2N
θ
orientations, φ
k
= kπ/N
θ
and
k = [0, N
φ
− 1]. This means that for each simple-
cell orientation on [0,π] there are two opposite anal-
ysis orientations on [0,2π], e.g., θ
1
= π/N
θ
results in
φ
1
= π/N
θ
and φ
9
= 9π/N
θ
; see Fig. 2 (top).
This division into response-analysis orientations
is acceptable, according to (Hubel, 1995), because a
typical cell has a maximum response at some orienta-
tion and its response decreases on both sides, from 10
to 20 degrees, after which it declines steeply to zero;
see also (du Buf, 1993). In addition, this division is a
compromise between the cost (CPU time) of the num-
ber of orientations and the accuracy of the results.
Classifying keypoints is not trivial, because re-
sponses of simple and complex cells, which code the
underlying lines and edges at the vertices, are unre-
liable due to response interference effects (du Buf,
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
308

Figure 1: Keypoint detection and annotation. Input scene
(top-left) with, on the 2nd row, keypoints detected at scales
λ = 6 (left) and 27 (right). The 3rd and 4th rows show anno-
tated keypoints at scales λ = {6, 12,18,27}. The top-right
image shows one quadrant of a black square against a ho-
mogeneous background (left) and noisy background (right),
both at λ = 6.
1993). This implies that responses must be analysed
in a neighbourhood around each keypoint, and the
size of the neighbourhood must be proportional to the
scale of the cells. The validation of the line and edge
orientations which contribute to the vertex structure is
based on an analysis of the responses of simple cells,
both R
E
s, j
and R
O
s, j
, and consists of three steps: (1) only
responses with small variations at three distances are
considered, (2) local maxima of the responses over
orientations are probed and the remaining orientations
are inhibited, and (3) responses of even and odd sim-
ple cells are matched in order to keep the orientations
which are common to both.
In step (1), at any scale and each orientation φ
k
the
responses of the simple cells on three circles around
the keypoint position, with radii λ/2, λ and 2λ, are
compared. Instead of only taking the responses at
φ
k
, the orientation intervals φ
k
± π/N
φ
are considered.
The three maximum responses of R
E/O
k,r
in the orien-
tation interval around k and at the three radii r are
detected, and their maximum
ˆ
R
k
= max
r
R
E/O
k,r
. Only
responses with small variations at the three radii are
considered (R > 0.6
ˆ
R
k
), yielding N
β
candidate ori-
entations. The smallest radius of λ/2 was chosen
because of the interference effects referred to above
(du Buf, 1993). The other two radii were determined
experimentally.
Biologically, the above process is based on clus-
ters of groupingcells with dendritic fields (Fig. 2 (top)
in red) covering the orientation intervals at each of
the three radii. These grouping cells combine other
cells with self-inhibition for non-maximum suppres-
sion. The three grouping cells at the three radii feed
into another grouping cell which compares the re-
sponses and which inhibits itself when the responses
are not similar. Figure 2 (bottom) shows responses
of simple cells in the case of a black square against
a noisy background (Fig. 1 top-right). It shows two
scales, λ = 6 (column 1 and 2) and λ = 15 (column 3
and 4), only three of all eight orientations (top to bot-
tom), even cells in columns 1 and 3 and odd cells in
columns 2 and 4. Dark levels are negative and bright
ones are positive. Also shown is one detected key-
point at each scale with, in red, the three circles at
λ/2, λ and 2λ at which the grouping cells are located.
The drawing at the top shows the orientation intervals,
also in red, covered by the dendritic fields in the case
of θ
1
with opposite orientations φ
1
and φ
9
.
In step (2), the responses at the detected orienta-
tions are summed,
¯
R = Σ
k
R
k
, and, for validation pur-
poses, all responses
ˆ
R
k
below a threshold value of
¯
R
are suppressed (0.95
¯
R/N
β
). Biologically, this is done
by another grouping cell which sums responses of the
grouping cells in step (1) and which may inhibit the
same cells if their response is too low.
If there also exist maximum responses
ˆ
R
k
at the
two neighbouring orientations φ
k−1
and φ
k+1
, they
will be inhibited if they are too low (
ˆ
R
k±1
< 0.95
ˆ
R
k
).
The abovevalues were determined by analysing many
objects like triangles, squares and polygons.
Step (2) is necessary because we need the orienta-
tions which convey the most consistent information,
i.e., not being due to varying lighting levels, light
sources casting shadows, background structures and
OPTICAL FLOW BY MULTI-SCALE ANNOTATED KEYPOINTS - A Biological Approach
309

Figure 2: Top: a few orientations of simple cells (θ) and
opposing orientations for keypoint classification (φ) plus, in
red, orientation intervals covered by grouping cells. Bot-
tom: responses of simple cells at 3 orientations (top to bot-
tom) and at two scales λ = 6 (left) and λ = 15 (right). From
left to right: responses of even and odd simple cells. Also
shown is one detected keypoint with, in red, the 3 circles on
which the responses are analysed for keypoint annotation.
even dynamic backgrounds like the wind playing the
crowns of trees. Figure 1 (top-right) shows the dif-
ference in the case of the same black square against a
homogeneous background (left) and a structured one
(right). The diagonal structure in the background has
a much lower contrast than the edge of the square.
Hence, without step (2) the keypoint would have been
annotated by three orientations instead of two.
The analysis in step (3) only concerns the match-
ing of equal orientations, i.e., inhibiting all orienta-
tions which have not been detected in the responses of
both even (R
E
s, j
) and odd (R
O
s, j
) simple cells. Remain-
ing orientations φ
k
are attributed to the keypoint, plus
the junction type K, L, T, +, etc. Again, the match-
ing is achieved by grouping cells which combine the
grouping cells devoted to R
E
s, j
and R
O
s, j
.
In the above procedure there is only one excep-
tion: keypoints at isolated points and blobs, especially
at very coarse scales, are also detected but they are not
caused by any line/edge junctions. Such keypoints are
labeled “blob” without attributed orientations.
The bottom four images in Fig. 1 show re-
sults of keypoint annotation at the four scales λ =
{6,12, 18,27}. At fine scale there are many keypoints
and at coarse scale less. Below, the annotated key-
points will be exploited in different processes. As
mentioned above, keypoint detection may occur in
cortical areas V1 and V2, whereas keypoint annota-
tion requires bigger receptive fields and could occur
in V4. Optical flow is then processed in areas V5/MT
and MST.
3 OPTICAL FLOW
Optical flow is determined by matching annotated
keypoints in successive camera frames, but only by
matching keypoints which may belong to the same
object. To this purpose we use regions defined
by saliency maps. Moreover, we do not consider
all scales independently, for two reasons: (1) non-
relevant areas of an image can be skipped because of
the hierarchical scale structure, and (2) by applying a
hierarchical tree structure, the accuracy of the match-
ing can be increased, therefore also increasing the ac-
curacy of the optical flow. The latter idea is based on
the strategies as employed in our visual system (Ro-
drigues and du Buf, 2009a; Bar, 2004).
3.1 Object Segregation
We apply a multi-scale tree structure in which at a
very coarse scale a root keypoint defines a single ob-
ject, and at progressively finer scales more keypoints
are added which convey the object’s details. However,
coarser scales imply bigger filter kernels and more
CPU time, so for practical reasons the coarsest scale
applied here will be λ = 27, which is a compromise
between speed and quality of results.
Below we use λ = [6,27] with ∆λ = 3, and at the
moment all keypoints at λ = 27 are supposed to rep-
resent individual objects, although we know that it is
possible that several of those keypoints may belong
to a same object. Each keypoint at a coarse scale is
related to one or more keypoints at one finer scale,
which can be slightly displaced. This relation is mod-
elled by down-projection using grouping cells with
a circular axonic field, the size of which (λ) defines
the region of influence. A responding keypoint cell
activates a grouping cell. Only if the grouping cell
is also excitated by responding keypoint cells at one
level lower (the next finer scale), a grouping cell at
the lower level is activated. This is repeated until the
finest scale has been reached. By doing so, all key-
points outside the areas of influence of the grouping
cells will not be considered, thus avoiding unneces-
sary computations. Figure 3 (top) illustrates the prin-
ciple of the linking process with cones representing
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
310
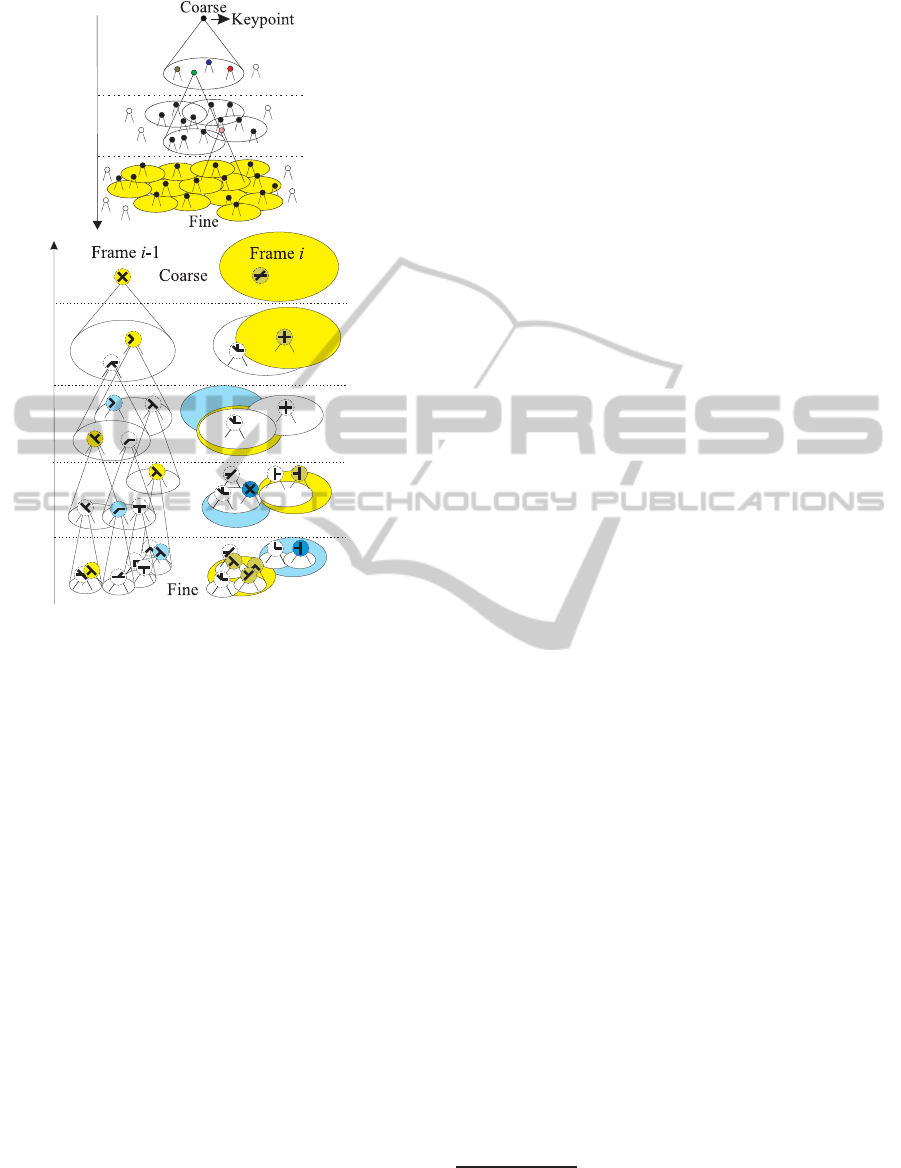
Figure 3: Top: hierarchical tree structure over scales. Bot-
tom: matching of annotated keypoints between successive
frames; see text for details.
the axonic fields of the grouping cells. At the finest
scale the region of influence of the keypoint at the
coarsest scale is indicated by the yellow area.
As mentioned above, at a very coarse scale each
keypoint – or central keypoint CKP – should corre-
spond to an individual object. However, at the coars-
est scale applied, λ = 27, this may not be the case and
an object may cause several keypoints. In order to
determine which keypoints could belong to the same
object we combine saliency maps with the multi-scale
tree structure.
A saliency map can be based on keypoints as these
code local image complexity (Rodrigues and du Buf,
2006). Such a map is created by summing detected
keypoints over all scales s, such that keypoints which
are stable over scale intervals yield high peaks, but
in order to connect the individual peaks and yield re-
gions a relaxation area is applied. As applied above,
the area is proportional to the scale and has a ra-
dius of λ. Here, we simplify the computation of
saliency maps by summing responses of end-stopped
cells at all scales, which yields similar results. Fig-
ure 6 (right) shows on the 2nd to the 4th row examples
of such saliency maps which correspond to the input
frames to their left. For illustration purposes the maps
were scaled to the interval [0,255]. The maps will be
thresholded in order to obtain segregated regions; see
below.
3.2 Keypoint Matching
At this point we have, for each frame, the tree struc-
ture which links the keypoints over scales, from
coarse to fine, with associated regions of influence
at the finest scale. We also have the saliency map
by summing responses of end-stopped cells over all
scales. The latter, after thresholding, yields segre-
gated regions which are intersected with the regions
of influence of the tree. Therefore, the intersected re-
gions link keypoints at the finest scale to segregated
regions which are supposed to represent individual
objects.
Now, each annotated keypoint of frame i can be
compared with all annotated keypoints in frame i− 1.
This is done at all scales, but the comparison is re-
stricted to an area with radius 2λ instead of λ at each
scale in order to allow for larger translations and ro-
tations. In addition: (1) at fine scales many keypoints
outside the area can be skipped since they are not
likely to match over large distances, and (2) at coarse
scales there are less keypoints, λ is bigger and there-
fore larger distances (motions) are represented there.
The tree structure is built top-down, Fig. 3 (top), but
the matching process, Fig. 3 (bottom), is bottom-up:
it starts at the finest scale because there the accuracy
of the keypoint annotation is better. Keypoints are
matched by combining three similarity criteria with
different weight factors: the distance D, the attributed
orientations O, and the tree correspondence C.
The distance D serves to emphasise keypoints
which are closer to the centre of the matching area.
For having D = 1 at the centre and D = 0 at radius
2λ, we use D = (2λ − d)/2λ with d the Euclidean
distance. Biologically, there may be no need to use
Euclidean distances if a kind of dynamic feature rout-
ing in space and time is used, possibly with motion
prediction in the “where” pathway.
1
Dynamic routing
from frame i − 1 to frame i, possibly also involving
previous frames i − 2 etc., is a spatiotemporal map-
ping, assuming a stack of neural layers in which a
few previous maps are stored: a new frame is al-
ways pushed on the “top-of-stack” and older frames
are also being pushed down. As for dynamic rout-
ing in invariantobject recognition, see (Rodriguesand
1
Motion prediction is a form of adaptation which could
explain the motion aftereffect, for example our illusion that
a railway station moves after our train has stopped. This
may occur in area MT (Kohn and Movshon, 2003).
OPTICAL FLOW BY MULTI-SCALE ANNOTATED KEYPOINTS - A Biological Approach
311

Figure 4: Top: dynamic routing between coarse keypoints
of successive frames (left), and cell representation of dis-
tance D (right). Bottom: cell representation of orientation
O (left), and tree correspondence C (right); see text for de-
tails.
du Buf, 2009a), the principle can be based on linking
first keypoints at very coarse scales (central keypoints
or CKP in Fig. 4 top-left) in space after which finer
scales refine the linking (Fig. 4 top-right). This is sub-
ject to ongoing research.
The orientation error O measures the differences
of the attributed orientations, but with a relaxation of
±π/N
θ
of all orientations such that also a small ro-
tation of the vertex structure is allowed. Similar to
D, the summed differences are combined such that
O = 1 indicates good correspondence and O = 0 a
lack of correspondence. Obviously, keypoints marked
“blob” do not have orientations and are treated sep-
arately. Biologically, the orientation error could be
based on the number of intermediate layers in the
routing which is necessary to establish correspon-
dence of the vertex structure, which is shown simpli-
fied in Fig. 4 (bottom-left).
Parameter C measures the number of matched
keypoints at finer scales, i.e., at any scale coarser than
the finest one. The keypoint candidates to be matched
in frame i and in the area with radius 2λ are linked
in the tree to localised sets of keypoints at all finer
scales. The number of linked keypoints which have
been matched is divided by the total number of linked
keypoints. This is achieved by sets of grouping cells
at all but the finest scale which sum the number of
linked keypoints in the tree, both matched and all.
Hence, parameter C describes the consistency of the
matching at a candidate’s position at the finer scales,
thereby influencing the matching of the candidate at
the actual scale. Figure 4 (bottom-right) illustrates
in colour the matched keypoints which influence the
matching at coarser scales; see also Fig. 3 (bottom).
The three parameters are combined by grouping
cells which can establish a link between keypoints in
frame i− 1 and i. Mathematically we use the similar-
ity measure S = αO+ βC+ γD, with α = 0.4, β = 0.3
and γ = 0.3. These values were determined empiri-
cally. The candidate keypoint with the highest value
of S in the area (2λ) is selected and the vector between
the keypoint in frame i − 1 and the matched one in
frame i is computed. The remaining candidates in the
area can be matched to other keypoints in frame i− 1,
provided they are in their local area. Keypoints which
cannot be matched are discarded.
Figure 5 (top-left) shows a sequence of 10 frames
with a moving and rotating star combined into one
image and, at right, examples of keypoints detected at
scales λ = 6 (left) and 24 (right), together with their
annotation below. The 2nd row (left) shows the opti-
cal flow vectors from the first to the last frame. The
other images show two superimposed frames with
egomotion of the camera and the optical flow vectors
at four scales λ = {6, 12,18,27}. It can be seen that
there are some but few errors. In principle, such out-
liers can be removed, but important is that the cor-
rect egomotion can be seen at all scales with, as ex-
pected, more variation at the finest scale. In fact, the
flow detected at the coarsest scale (bottom-right) is
already sufficient to extract the egomotion. This is
consistent with object categorisation and recognition
(Bar, 2004; Oliva and Torralba, 2006; Rodrigues and
du Buf, 2009b): coarse-scale information is available
first and this is used for a first but rough categorisation
(80 – 100 ms), after which information at finer scales
becomes available to refine the categorisation.
After obtaining egomotion vectors at the coarsest
scale, by averaging but perhaps after elimination of
outliers in local neighbourhoods because of possible
camera rotation, egomotion can be eliminated by sub-
tracting this information from all flow vectors (War-
ren and Rushton, 2009). Bearing this in mind, when
we compute the tree correspondence C for keypoint
matching at only the coarsest scale, the result will be
similar. However, the result will be more robust if
we use all scales, as in the object categorisation and
recognition process (Rodrigues and du Buf, 2009b).
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
312

Figure 5: Optical flow results. Top-left: frames with a mov-
ing and rotating star combined into one image. Top-right:
detected keypoints at scales λ = 6 (left) and 24 (right), with
the annotated keypoints below. Second from top, at left, op-
tical flow vectors. The other images show two combined
frames with egomotion of the camera and optical flow vec-
tors at scales λ = {6,12,18,27}.
4 TRACKING OF OBJECTS
After thresholding, the saliency map of a frame yields
separated regions-of-interest(RoI); see Fig. 6, the 2nd
to 4th row at right. These regions can be intersected
with the regions as defined by the tree structure, in
Fig. 3 (top) shown in yellow. The regions of the den-
dritic fields of the end-stopped cells which generate
the saliency map will overlap the regions of the ax-
onic fields of the keypoint-grouping cells in the tree
structure. Hence, neighbouring keypointsare grouped
together in the RoIs and their displacement vectors
after the matching process yield the optical flow of
segregated image regions, i.e., where an individual
object or a combination of connected (sub)objects is
or are moving. In order to discard very small opti-
cal flow due to the camera’s motion (not significant
egomotion; see above) and to obtain more robust re-
sults, optical flow vectors are only computed if at at
least four scales the matched keypoints in successive
frames have displacement vectors with a length which
is bigger than one pixel.
Figure 6 (top) shows a montage of a sequence with
a moving robot car (at left) and the tracked optical
flow vectors (at right): in white for λ = 6 and in red
for λ = 27. Rows 2 to 4 show frames with the robot
car segregated in a box (at left) and the correspond-
ing saliency maps (at right). The bottom row shows
zooms of two frames with flow vectors at scale λ = 9.
Figure 7 shows two more sequences with moving
persons. The top sequence shows a moving person far
away, with the bounding box and tracked motion (ar-
rows). The bottom sequence shows a person at close
range, in which case the different motions of the dif-
ferent body parts can be distinguished, also the mo-
tion of the shadow. The bottom sequence illustrates
a real application: detecting and tracking moving ob-
stacles on paths and sidewalks, which is for a naviga-
tion aid for the blind in the context of the SmartVision
project. In this case the optical flow is complemented
by the borders of the path and their intersection in the
vanishing point, and the tracking of the centre of the
bounding box relative to the vanishing point can be
used to detect if the obstacle is approaching or not,
for obstacle avoidence.
5 CONCLUSIONS
In a previous paper we have shown that keypoint
scale-space provides very useful information for con-
structing saliency maps for Focus-of-Attention(FoA),
and that faces can be detected by grouping facial land-
marks defined by keypoints at eyes, nose and mouth
(Rodrigues and du Buf, 2006). We have also shown
that line/edge scale-space provides very useful infor-
mation for face and object recognition (Rodrigues
and du Buf, 2009b). Obviously, object detection and
recognition are related processes, with a seamless in-
tegration in the where and what pathways. However,
there is no (known) dichotomy in the sense that key-
points are only used in the where pathway and lines
OPTICAL FLOW BY MULTI-SCALE ANNOTATED KEYPOINTS - A Biological Approach
313

Figure 6: Top: a sequence with a moving robot car (left)
and combined optical flow vectors (right), in white at a fine
scale and in red at a coarse scale. Rows 2 to 4 show frames
with the robot car segregated in a box (left) and the cor-
responding saliency maps (right). The bottom row shows
zooms of optical flow vectors at scale λ = 9.
and edges only in the what pathway.
In this paper we showed that keypoint detection
Figure 7: Two sequences with moving persons. The per-
sons have been segregated (bounding box) and tracked (top
sequence; arrows), and differently moving body parts have
been detected, including shadows (bottom sequence).
can be complemented by keypoint annotation, and
that annotated keypoints in a hierarchical tree struc-
ture can be used for keypoint matching in order to
obtain optical flow. In addition, since local clusters
of keypoints are mostly related to individual moving
objects, object segregation can be achieved and ob-
jects can be tracked. As written before, cortical areas
MT and MST are involved in optical flow and egomo-
tion, but recent results obtained with fMRI showed no
clear neural activity in their ventral (what) and dor-
sal (where) subregions, but elevated activity in be-
tween the subregions (Smith et al., 2006). This might
indicate that optical flow at MT level is processed
separately or involves both pathways. The fact that
optical flow can be used to obtain object segrega-
tion, as demonstrated here, in addition to our previous
experiments concerning saliency maps for FoA and
face detection, in all cases only using keypoint scale
space, would indicate some “preference” of the dorsal
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
314

(where) pathway for keypoints. This idea is strength-
ened by the fact that area MT also plays a role in
the motion-aftereffect illusion (Kohn and Movshon,
2003), which is tightly related to motion adaptation
and prediction. Therefore, motion prediction might
play a very important role in the dorsal pathway, not
only where objects are now but also where they are
expected next. Such predictions tied to objects may
lead to much more efficient processing, for exam-
ple in robot vision, because most image regions can
be skipped. Nevertheless, robot vision also requires
some sort of “arousal” system for spotting new or un-
expected moving objects.
Having a model for matching keypoints in con-
secutive time frames for optical flow, the same prin-
ciple can be applied to stereo (disparity), matching
left and right frames. Since information of one of the
two frames is already available for optical flow, the re-
quired additional CPU time will be limited, especially
if only the distance of moving objects is necessary, for
example to detect objects which may be on collision
course, with and without egomotion. In general, how-
ever, disparity can be used for obtaining a 3D sketch
of an entire scene, plus the 3D structure of individual
objects in the scene which may complement the (2D)
line/edge scale space for object recognition. More-
over, optical flow and disparity can be combined to
obtain more robust object segregations.
Keypoints can complement the line/edge coding
in attributing depth, not only to vertical lines and
edges but also line and edge junctions. This results
in a sort of 3D “wireframe” representation as used in
modelling solid objects in computer graphics. The
fact that projections from left and right eyes are very
close in the cortical hypercolumns and that many sim-
ple and complex cells are also disparity tuned sug-
gests that our visual system processes 3D objects in
the same way, probably simplifying 3D object recog-
nition.
ACKNOWLEDGEMENTS
Portuguese Foundation for Science and Technol-
ogy (FCT) through the pluri-annual funding of
the Inst. for Systems and Robotics (ISR/IST), the
POS Conhecimento Program with FEDER funds, and
FCT project SmartVision (PTDC/EIA/73633/2006).
REFERENCES
Bar, M. (2004). Visual objects in context. Nature Rev.:
Neuroscience, 5:619–629.
du Buf, J. (1993). Responses of simple cells: events, inter-
ferences, and ambiguities. Biol. Cybern., 68:321–333.
Duffy, C. and Wurtz, R. (1991). Sensitivity of mst neu-
rons to optic flow stimuli. I. A continuum of response
selectivity to large-field stimuli. J. Neurophysiol.,
65(6):1329–1345.
Hubel, D. (1995). Eye, Brain and Vision. Scientific Ameri-
can Library.
Kohn, A. and Movshon, J. (2003). Neuronal adaptation to
visual motion in area mt of the macaque. Neuron,
39:681–691.
Morrone, M., Tosetti, M., Montanaro, D., Fiorentini, A.,
Cioni, G., and Burr, D. (2000). A cortical area that
responds specifically to optic flow, revealed by fMRI.
Nature Neuroscience, 3(7):1322 – 1328.
Oliva, A. and Torralba, A. (2006). Building the gist of a
scene: the role of global image features in recognition.
Progress in Brain Res.: Visual Perception, 155:23–26.
Orban, G., Lagae, L., Verri, A., Raiguel, S., Xiao, D., Maes,
H., and Torre, V. (1992). First-order analysis of optical
flow in monkey brain. PNAS, 89(7):2595–2599.
Rodrigues, J. and du Buf, J. (2006). Multi-scale keypoints
in V1 and beyond: object segregation, scale selection,
saliency maps and face detection. BioSystems, 2:75–
90.
Rodrigues, J. and du Buf, J. (2009a). A cortical frame-
work for invariant object categorization and recogni-
tion. Cognitive Processing, 10(3):243–261.
Rodrigues, J. and du Buf, J. (2009b). Multi-scale lines and
edges in v1 and beyond: brightness, object categoriza-
tion and recognition, and consciousness. BioSystems,
95:206–226.
Smith, A., Wall, M., Williams, A., and Singh, K. (2006).
Sensitivity to optic flow in human cortical areas
mt and mst. European Journal of Neuroscience,
23(2):561–569.
Wall, M. and Smith, A. (2008). The representation of ego-
motion in the human brain. Current Biology, 18:191–
194.
Warren, P. and Rushton, S. (2009). Optic flow process-
ing for the assessment of object movement during ego
movement. Current Biology, 19(19):1555–1560.
William, K. and Charles, J. (2008). Cortical neuronal re-
sponses to optic flow are shaped by visual strategies
for steering. Cerebral Cortex, 18(4):727–739.
Wurtz, R. (1998). Optic flow: A brain region devoted to
optic flow analysis? Current Biology, 8(16):R554–
R556.
OPTICAL FLOW BY MULTI-SCALE ANNOTATED KEYPOINTS - A Biological Approach
315
