RESOURCE BOUNDED DECISION-THEORETIC BARGAINING

WITH FINITE INTERACTIVE EPISTEMOLOGIES

Paul Varkey and Piotr Gmytrasiewicz

Department of Computer Science, University of Illinois at Chicago, 851 S. Morgan St., Chicago, U.S.A.

Keywords:

Bilateral bargaining, Decision theory, Interactive epistemology, Bounded rationality, Memoization.

Abstract:

In this paper, we study the problem of bilateral bargaining under uncertainty. The problem is cast in an in-

teractive decision-theoretic framework, in which the seller and the buyer agents are equipped with the ability

to represent and reason with (probabilistic) beliefs about strategically relevant parameters, the other agent’s

beliefs, the other agent’s beliefs about the current agent’s beliefs, and so on up to ﬁnite levels. The inescapable

intractability of solving such models is characterized. We present a realization of the paradigm of (resource)

bounded rationality by achieving a trade-off between optimality and efﬁciency as a function of the discretiza-

tion resolution of the inﬁnite action space. Memoization is used to further mitigate complexity and is realized

here through disk-based caching. In addition, the inevitability of model extinction that arises in such settings

is dealt with by indicating an intuitive realization of the absolute continuity condition based on maintain-

ing an ensemble model, for e.g. a random model, that accounts for all actions not already accounted for by

other models. Our results clearly demonstrate an operationalizable scheme for devising computationally efﬁ-

cient anytime algorithms on interactive decision-theoretic foundations for modeling (higher-order) epistemic

dynamics and sequential decision making in multi agent domains with uncertainty.

1 INTRODUCTION

In strategic multi agent interactions under uncertainty,

modeled in a decision-theoretic framework, it is im-

portant for an agent to reﬂect upon its (partial) knowl-

edge of the strategically relevant parameters of the

interaction and the (partial) knowledge of the oppo-

nents as it deliberates about what course of action is

best (i.e. attains highest expected utility). The phe-

nomenon of an interactive epistemology of mutual

beliefs naturally arises – an agent may form beliefs

about the parameters to represent its uncertainty, be-

liefs about other agents’ beliefs, beliefs about other

agents’ beliefs about others’ beliefs, and so on. Then,

(Bayesian) probability calculus provides a ﬂexible

and powerful means of representing and reasoning

about the resultant epistemic dynamics.

An immediate difﬁculty that arises in this frame-

work is the potential inﬁniteness of the interactive

epistemology. In game theory, esp. in the literature

on games under incomplete information, beginning

with John Harsanyi’s seminal work on this problem

(Harsanyi, 1968), there is a long tradition of work that

has been systematically addressing this issue. See, for

e.g., (Zamir, 2008) for a survey.

The game-theoretic approach centers around the

notion of an equilibrium. Particular epistemic as-

sumptions (Aumann and Brandenburger, 1995) are

necessary in order to achieve equilibirum – such as

may never be the case in an actual interaction. In

addition, many games, especially under incomplete

information, exhibit the phenomena of a multiplicity

of equilibria, with no means of uniquely identifying

“the” rational chouce from among them. Therefore,

the game-theoretic approach is limited in its ability to

prescribe a generally applicable control paradigm for

the design of intelligent autonomous agents.

A purely subjective approach of dealing with

this issue in a decision-theoretic framework was re-

cently proposed and has led to deﬁnition of a ﬁnite

interactive epistemological decision theoretic model

(DT-FIE, from here on) called the Finitely Nested

I-POMDP ((Gmytrasiewicz and Doshi, 2005) and

(Doshi and Gmytrasiewicz, 2005)). In that work, the

standard POMDP model (Lovejoy, 1991) and (Kael-

bling et al., 1998) is extended by equipping an agent

with the ability to maintain interactive (i.e. higher-

order) beliefs, up to some ﬁnite level. The standard

theory of sequential decision making is then extended

to this model to produce optimal policies. The analy-

219

Varkey P. and Gmytrasiewicz P..

RESOURCE BOUNDED DECISION-THEORETIC BARGAINING WITH FINITE INTERACTIVE EPISTEMOLOGIES.

DOI: 10.5220/0003176802190225

In Proceedings of the 3rd International Conference on Agents and Artiﬁcial Intelligence (ICAART-2011), pages 219-225

ISBN: 978-989-8425-41-6

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

ses in this paper are inspired by that work.

The problem of bilateral bargaining under uncer-

tainty is a well-known example of a multi agent se-

quential decision-making problem under uncertainty

and is well-studied in game-theoretic literature: see,

in order, (Rubinstein, 1982), (Rubinstein, 1985), (So-

bel and Takahashi, 1983), (Cramton, 1984), (Fuden-

berg and Tirole, 1983), (Grossman and Perry, 1986),

(Perry, 1986) and (Cho, 1990).

The incompleteness of the theory, from a predic-

tive as well as a prescriptive perspective, motivates

this work, in which our main objective is the realiza-

tion of an operationalizable automated DT-FIE bar-

gaining agent.

The paper is organized as follows. In the next sec-

tion, we introduce notation and set up the model. In

the following sections, we introduce and study seller

and buyer agents of successively increasing sophisti-

cation and present our various results in their appro-

priate contexts. Our main result regarding the real-

ization of bounded rationality is presented in Section

5.2, where we discuss the L2Seller type.

2 PRELIMINARIES

In this paper, we investigate a seller-offers bargain-

ing mechanism where, at every turn, the seller makes

offers and the buyer indicates whether or not a partic-

ular offer is acceptable. The game ends when an offer

is accepted unless the game has a ﬁnite horizon, in

which case it ends, possibly without agreement, when

the horizon is encountered. Delay in reaching agree-

ment is costly to either party – realized by applying

a multiplicative discount factor δ to the payoffs ($1

today is worth only $δ

dollars n days from now).

The agents ascribe a valuation to the item bar-

gained over – say c for the seller and v for the buyer.

Assume also that trade is feasible, i.e. c ≤ v. If agree-

ment is reached on the n-th stage at some price, say

x, where c ≤ x ≤ v, the payoffs to the seller and the

buyer are (x−c)·δ

n−1

and (v− x)· δ

n−1

, respectively.

It is assumed throughout that c = 0 and c ≤ v ≤ 1

(i.e. v ∈ [0, 1]) and that 0 ≤ δ ≤ 1. All this is assumed

to be commonly known; while, v itself is assumed to

be the buyer’s private information. Agents may main-

tain other relevantbeliefs and higher-order beliefs; for

e.g. the seller may maintain a belief about the buyer’s

valuation, the buyer may maintain a second-order be-

lief about the seller’s ﬁrst-order belief about its (i.e.

the buyer’s) valuation, etc. There is nothing special

about this particular informational setting; the con-

clusions easily generalize to settings where the basic

strategically relevant uncertainty is about something,

or, set of things, other than the buyer’s valuation.

Here, we recall and adopt notations from (Gmy-

trasiewicz and Doshi, 2005) to describe the agents’ in-

teractive epistemological sophistication. An Li-type

(class) for i = 1, 2..., where type is either Buyer or

Seller, denotes an agent type (class) that can model

and reason about agents of Lj-type (class), where

0 ≤ j < i. For e.g., the L2-type agent can represent

and reason about L0-type and L1-type agents, etc.

2.1 Deﬁnitions

In the following, we introduce additional notation and

deﬁnitions to make certain notions precise:

(Li)AgentA

LjAgentB

. The number of possible (Li-)AgentA

types (or, type classes, as should be clear from the

context) in the support of the Lj-AgentB’s initial

prior belief. For e.g., n

L0Buyer

L1Seller

represents the num-

ber of L0-Buyer type classes in the L1-Seller’s

prior support, and n

L1Seller

L2Buyer

represents the number

of L1-Seller types in the L2-Buyer’sprior support.

|V|. The cardinality of the discretized space of possi-

ble buyer valuations.

mpd. The minimum proﬁt demanded by the buyer.

Schedule. A (possibly ﬁnite) sequence of offers

{x1, x2, x3, ...}, where each successive offer is

made after the rejection of the previous one. We

assume a discretized space of possible offers, O.

We also assume that offer schedules are mono-

tonically decreasing. These ensure, usefully, the

ﬁniteness of the space of possible offer schedules.

An optimal schedule is one that achieves the

maximum expected utility with respect to some

(implicit) initial prior belief.

|O|. The cardinality of the discretized space of possi-

ble actions (offers).

Terminal Belief. A state of belief that need not be

explored (i.e. deliberated upon) further and can

be trivially assigned a value; for e.g. the belief

state of the (seller) agent upon encountering the

horizon of the game or after the lowest possible

potentially proﬁtable offer was just rejected, etc.

Belief-state Graph. A labelled directed graph where

all possible belief states of an agent constitute the

nodes (or, vertices) and where there is a directed

edge from a node u to a node v labelled with offer

a if the agent’s belief state changes from u to v

after performing Bayes’ belief update conditional

on the event that offer a was rejected.

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

220

3 L0-TYPE AGENTS

L0-type agents, the least sophisticated in this study,

have the capability to model the world and may have

preferences and intentions (to realize them). They do

not explicitly model other similarly intentional agents

(though, their presence may be ‘modelled’ as environ-

mental artifact or noise). The classic POMDP would

be classiﬁed as an L0-type model.

We consider a class of L0-Seller types equipped

with a simple offer generation rule: Decrement the

most recently rejected offer, if any, by some (ﬁxed or

random) amount. We assume a smallest discretiza-

tion unit for the action space, denoted as d and a mul-

tiplicative factor, denoted by m. The L0-Seller starts

with some initial offer and then decrement the cur-

rently outstanding offer by some constant amount md,

or some random amount sampled uniformly from all

possible offers that are lesser than the outstanding one

by some multiple of md, denoted respectively as L0-

Seller(md) and L0-Seller(mdr). Offers cease as soon

as one is accepted, or, if continuation is detrimental.

Example 1. Let d = 0.05. Let the outstanding of-

fer be 0.4. Then, for instance, an L0-Seller(2d)

would next offer 0.3(= 0.4 − 2 × 0.05) and an L0-

Seller(3rd) would select some offer uniformly in

{0.05, 0.2, 0.35}.

We consider L0-Buyer types with equally simplis-

tic decision behavior: a buyer with valuation v accepts

the outstanding offer x if (and only if) v − x ≥ mpd.

An L0-Buyer type is, therefore, characterized by its

valuation and mpd. We group together L0-Buyer

types with the same mpd into a type class.

4 L1-TYPE AGENTS

4.1 L1-seller

At every stage, the seller can compute the probability

that a given offer will be rejected, based on its cur-

rent belief. If the offer is indeeed rejected, the seller

updates its beliefs in a Bayesian manner, and the de-

liberation continues, until a terminal belief is encoun-

tered. This mechanism induces a directed delibera-

tion tree as the connected subgraph of the belief state

graph, where the root node is the initial prior belief

and every leaf node is a terminal belief. A particular

offer schedule, therefore, corresponds to a particular

set of paths on this tree from the root node to a termi-

nal node. An expected probability may be computed

for each path, which induces an expected utility for

each offer schedule. The seller’s task is to chose an

optimal schedule, with respect to its prior beliefs.

The complexity of the straightforward optimal

top-down traversal approach, is equal to the total

number of nodes in the deliberation tree, namely, 2

|O|

This result is obtained as a consequence of the fact

that, at every stage, the seller need not again consider

offers greater than or equal to rejected offers.

In the bottom-up approach, the seller ﬁrst solves

all terminal belief states, followed, successively, by

solving all belief states that have a directed edge in

the belief state graph to some previously solved state.

This process is complete when the root belief state is

encountered and solved. The associated complexity

depends on the number of unique belief states and can

be shown to be |V|

L0Buyer

L1Seller

Therefore, the running-times of both approaches

are exponential; the top-down approach in the dimen-

sion of the action space and the bottom-up approach

in the dimension of one component of the state space.

These values are not directly comparable; therefore,

there does not, a priori, seem to be a natural better

alternative among the two approaches.

It turns out that, in the particular case of the

L1Seller,it is possible to elegantly characterize reach-

able belief states which is then used to devise a

polynomial-time algorithm for the bottom-up ap-

proach. Due to space limitations, this is outlined only

in our technical report (Varkey, 2010). However, such

characterizations are not simple to achieve in gen-

eral. In Section 5.2, we analyze the L2-Seller and

present, as our main contribution, a boundedly ratio-

nal top-down scheme that is applicable to general Li-

type sellers.

4.2 L1-buyer

A buyer with valuation v accepts an offer x if the im-

mediate sure proﬁt (= v − x) is greater than the dis-

counted expected proﬁt from the next stage. It cal-

culates this expected proﬁt from what it expects to be

the next offer based on its beliefs, updated after seeing

the current offer x, about the seller.

This online decision-making computation is linear

in the number of mental models maintained by the

buyer, i.e. O(n

L0Seller

L1Buyer

)). Two examples follow.

Example 2. Suppose that the buyer, assumed to

have a valuation of 0.9, believes, with probabilities

0.7 and 0.3, respectively, that the seller is one of two

types – a subintentional automaton with a ﬁxed sched-

ule of offers, say {1.0, 0.8, 0.7, 0.4, 0.3, 0.2, 0.1}, or

an L0-Seller(2d) type. Call these Model 1 and Model

2, respectively. Suppose that the actual seller follows

RESOURCE BOUNDED DECISION-THEORETIC BARGAINING WITH FINITE INTERACTIVE EPISTEMOLOGIES

221

the schedule {1.0, 0.8, 0.6, 0.4, 0.3, 0.2, 0.1}. Also as-

sume that d = 0.1 and δ = 0.7.

The buyer’s belief updates and decisions at every

stage are recorded in Table 1.

Both seller models may be used to rationalize the

ﬁrst two offers. In these cases, Bayesian belief update

simply preserves the prior. The buyer rejects both

these offers because the discounted expected proﬁt

from the next stage is greater. The next offer, 0.6, is

only rationalizable using Model 2. Therefore, the up-

dated belief concentrates the entire probability mass

on this model. The discounted expected proﬁt from

the next stage is still greater – therefore, 0.6 too is

rejected. Finally, offer 0.4 is accepted.

4.2.1 Model Extinction and ACC

Example 2 usefully demonstrates the necessity and

sufﬁciency of the absolute continuity condition(ACC)

(Kalai and Lehrer, 1993) in an interactive decision-

making framework. Both models thought possible by

the buyer are wrong (in the sense that neither of them

represents the true seller). In fact, after the buyer re-

ceives offer 0.6, it (correctly) deems that the seller

cannot possibly be Model 1, and, therefore, removes

this model from the support of its beliefs. However, it

turns out that Model 2 accounts for the buyer’s obser-

vations all the way until the termination of the inter-

action (which happens when the buyer accepts offer

0.4). But note, in particular, that Model 2 is also a

wrong model of the true seller. Interestingly enough,

had the negotiations continued for one more round,

the next offer of 0.3 would have led the buyer to con-

clude that not even Model 2 could be the true model

of the seller, leading to the extinction of all models

in the buyer’s prior belief space. None of the prior

models it thought possible to begin with could suc-

cessfully explain (rationalize) reality; it realizes that

it was completely mistaken in its beliefs.

How should Bayesian decision-theoretic agents

prepare for such contingencies in multi-agent en-

vironments where it is uncertain about the type of

agent(s) with which it is interacting? As in our ex-

ample, consider an agent that starts with a prior belief

over a non-exhaustive set of possible models of the

opponent agent. If one of these models happens to be

the true model of the opponent, then our agent will

never be taken by surprise. In fact, after sufﬁcient in-

teraction and observation, its beliefs will converge to

the true model (Kalai and Lehrer, 1993). If, on the

other hand, its beliefs do not contain the true model

in its support, then, barring a fortuitous satisfaction

of ACC, the agent will eventually be completely sur-

prised (an eventual extinction of all models in its be-

lief support).

Realization of ACC through Random Models. A

closer understanding of such an agent’s beliefs yields

a way out of this quandary. If an agent is so com-

pletely mistaken in its beliefs that the true model is not

even possible a priori, it is only natural that it even-

tually faces inexplicable situations. A more realistic

approach calls for a cautious agent that includes, in

the support of its beliefs, one more model – a random

model – which would make all actions (here, offer ev-

ery possible offer) plausible with some positive prob-

ability, and, thereby, account for all contingent behav-

ior (not already modeled by the other models). Such

a prior belief will always satisfy ACC. The following

example illustrates the usefulness of this approach.

Example 3. Consider a buyer, with valuation 0.7,

who believes, with probabilities 0.5, 0.4 and 0.1, re-

spectively, that the seller is one of three possible

types – a subintentional automaton with a ﬁxed sched-

ule of offers, say {1.0, 0.9, 0.7, 0.4, 0.3, 0.2, 0.1}, or

an L0-Seller(d) type, or an L0-Seller(dr) type. Call

these Model 1, Model 2 and Model 3 respectively.

Suppose that the actual seller follows the schedule

{1.0, 0.9, 0.8, 0.7, 0.5, 0.3, 0.1}. As before, assume

that d = 0.1 and δ = 0.7.

The buyer’s belief updates and decision-making at

every stage are recorded in Table 2.

We observe that Model 1 is removed (from the

support of beliefs) when offer 0.8 is recieved. Model

2 is removed when 0.5 is recieved – leaving only the

random model, Model 3. Since this model rational-

izes every possible offer, the buyer is able to continue

interacting and eventually accepts 0.3.

5 L2-TYPE AGENTS

5.1 L2-buyer

The L2-Buyer “pre-solves” all its L1-Seller mental

models ofﬂine, incurring, in the process, an (ofﬂine)

polynomial time cost of



L1Seller

L2Buyer



|O|

× n

L0Buyer

L1Seller



Following this, its online operation is similar to that

of the L1-Buyer. Whenever an offer is recieved, it up-

dates its beliefs and decides whether or not to accept

by comparing the immediate proﬁt with the expected

proﬁt from the next stage – both of which are linear

time computations in the number of mental models –

namely, O



Seller

L2Buyer



ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

222

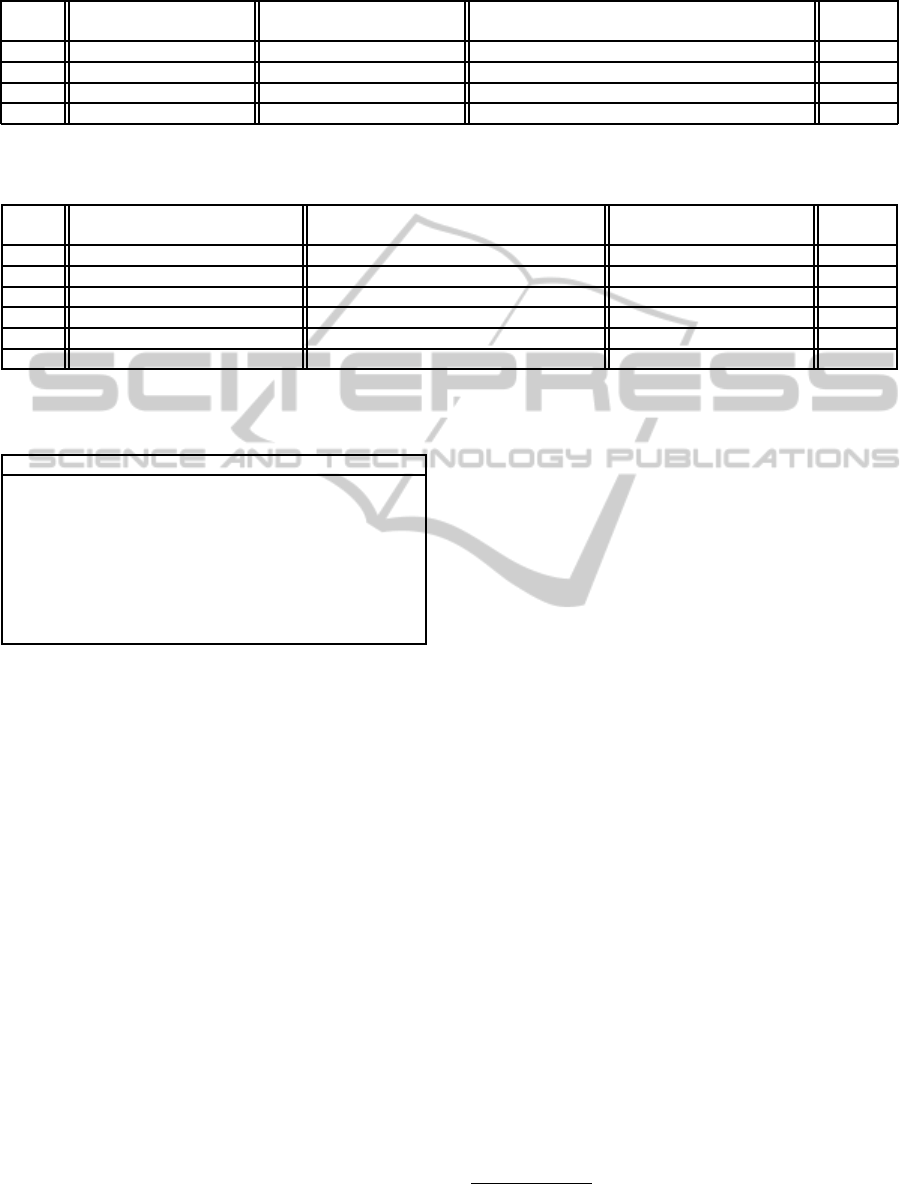
Table 1: Example 2: L1-Buyer’s belief update and sequential reasoning; v = 0.9, δ = 0.7.

Offer

Belief Expected Expected Proﬁt Accept/

Update Next Offer On Reject Reject

1.0 Both models survive 0.7· 0.8+ 0.3· 0.8 = 0.8 0.7· (0.9− 0.8) = 0.07 > −0.1(= 0.9− 1.0) Reject

0.8 Both models survive 0.7· 0.7+ 0.3· 0.6 = 0.67 0.7· (0.9−0.67) = 0.161 > 0.1(= 0.9−0.8) Reject

0.6 Only Model 2 survives 1· 0.4 = 0.4 0.7· (0.9− 0.4) = 0.35 > 0.3(= 0.9− 0.6) Reject

0.4 Model 2 survives 1· 0.2 = 0.2 0.7· (0.9− 0.2) = 0.49 < 0.5(= 0.9− 0.4) Accept

Table 2: Example 3: L1-Buyer that includes random L0-Seller model in support of prior beliefs; v = 0.7, δ = 0.7.

Offer

Belief Expected Expected Proﬁt Accept/

Update Next Offer On Reject Reject

1.0 All models survive 0.5· 0.9+ 0.4· 0.9+ 0.1· 0.5 = 0.86 < 0 Reject

0.9 All models survive 0.5· 0.7+ 0.4· 0.8+ 0.1· 0.45 = 0.715 < 0 Reject

0.8 Model 2 and Model 3 survive 0.8· 0.7+ 0.2· 0.4 = 0.64 0.7· (0.7− 0.64) = 0.042 Reject

0.7 Model 2 and Model 3 survive 0.8· 0.6+ 0.2· 0.35 = 0.55 0.7· (0.7− 0.55) = 0.105 Reject

0.5 Only Model 3 survive 1· 0.25 = 0.25 0.7· (0.7− 0.25) = 0.315 Reject

0.3 Model 3 survives 1· 0.15 = 0.15 0.7· (0.7− 0.15) = 0.385 Accept

Table 3: Column index symbol legend for Table 4.

Symbol Description

d The discretization unit

τ Time horizon ∈ {1, 2, 3, ...} ∪ inf

optimal schedule The optimal schedule of offers

θ The optimal expected proﬁt

c Number of actual computations

′

Maximum number of computations

ˆµ Executions times (in secs)

5.2 L2-seller

We note ﬁrst that a straightforward bottom-up dy-

namic programming is optimal but incurs a time com-

plexity of an order equal to the number of possible

belief states, which is doubly exponential in the di-

mension of the state space.

5.2.1 Memoization using Disk-based Caching

This extreme intractibility leads to a reexamination of

the top-down approach, which, as noted previously,

incurs an exponential time-complexity of O(2

|V|

). An

immediate enhancement that may used to mitigate

this complexity involvescaching the computed results

on disk. This caching scheme is called memoization

and works best when there are many redundancies. In

the worst-case, there are no redundancies, and the en-

tire computation tree will be stored on disk.

As before, the seller’s initial belief state and the

belief state graph induces a top-down deliberation

tree. At each belief state, the seller ﬁrst checks to see

if the solution is already available, in which case, it

was previously encountered, solved and cached. Else,

it proceeds to solve it by considering all and only of-

fers lesser than previously rejected ones. Whenever

the computation encounters a terminal belief state or

whenever it evaluates all possible offers for a given

belief state, it ascends up the deliberation tree. In the

latter case, the belief state under considerationis com-

pletely solved, in the sense that the algorithm has eval-

uated all possible offers at this state and has computed

the best offer (along with the expected proﬁt associ-

ated with this offer). This solution is then cached on

disk – in particular, in our implementation it is stored

in a relational database

. The solution is indexed by

a complete speciﬁcation of the entire belief state. In

Section 6 we present considerable empirical evidence

for the practical usefulness of memoization.

5.2.2 Realization of Bounded Rationality

The unavailability of a general analytical solution for

multiagent sequential planning under uncertainty and

the infeasibility of searching through the uncountable

space of all possible schedules using a discrete algo-

rithm necessitates our discretized dynamic program-

ming approach. It was noted earlier that the worst-

case complexity incurred is exponential in the dimen-

sion of the action space (i.e discretized space of possi-

ble offers). It is in the context of this characterization

that we recast our top-down deliberation tree traversal

approach under the paradigm of bounded rationality.

A ﬁner discretization considers a strict superset of the

space of available policies than a coarser one. There-

fore, a ﬁner discretization, though slower, is more op-

sqlite3 serves as our database backend

RESOURCE BOUNDED DECISION-THEORETIC BARGAINING WITH FINITE INTERACTIVE EPISTEMOLOGIES

223

Table 4: Experimental results for L2-Seller Ann.

d τ optimal schedule θ



c, c

′

∑

min(⌊

0.9

+1⌋,τ)

k=0



⌊

0.9

+1⌋



ˆµ

0.02 inf 0.48→0.28→0.2→0.14→0.12→0.1 0.216036 174, 70368744177664 17.861, 17.826

0.02 7 0.48→0.28→0.2→0.14→0.12→0.1 0.216036 610, 64441700 64.328, 62.477

0.02 6 0.48→0.28→0.2→0.14→0.12→0.1 0.216036 513, 10917020 52.626, 52.501

0.02 5 0.48→0.28→0.2→0.14→0.1 0.215916 408, 1550201 41.153, 41.418

0.02 4 0.48→0.28→0.18→0.12 0.214824 295, 179447 29.369, 29.228

0.02 3 0.46→0.26→0.18 0.212658 174, 16262 16.94, 16.426

0.02 2 0.48→0.28 0.21224 45, 1082 4.512, 4.768

0.05 inf 0.55→0.3→0.2→0.15→0.1 0.205083 66, 524288 6.536, 6.252

0.05 6 0.55→0.3→0.2→0.15→0.1 0.205083 162, 43796 14.958, 14.774

0.05 5 0.55→0.3→0.2→0.15→0.1 0.205083 138, 16664 12.759, 13.378

0.05 4 0.55→0.3→0.2→0.15 0.203733 106, 5036 9.575, 9.763

0.05 3 0.55→0.3→0.2 0.201405 66, 1160 6.111, 5.988

0.05 2 0.6→0.35 0.202639 18, 191 2.029, 1.774

0.1 inf 0.5→0.3→0.2→0.1 0.201527 30, 1024 3.09, 2.916

0.1 5 0.5→0.3→0.2→0.1 0.201527 49, 638 4.729, 4.5

0.1 4 0.5→0.3→0.2→0.1 0.201527 43, 386 3.916, 3.891

0.1 3 0.5→0.3→0.2 0.199453 30, 176 2.9, 2.8

0.1 2 0.6→0.4 0.2 9, 56 1.264, 1.192

0.2 inf 0.5→0.3→0.1 0.18025 10, 32 1.118, 1.242

0.2 4 0.5→0.3→0.1 0.18025 11, 31 1.41, 1.277

0.2 3 0.7→0.5→0.3 0.190684 10, 26 1.287, 1.125

0.2 2 0.5→0.3 0.197568 4, 16 0.658, 0.741

timal than a coarser one. Substantial empirical evi-

dence is presented in the next subsection in support

of this claim.

In principle, a contract algorithm can be devised

to exploit this tradeoff by choosing a discretization

unit such that the maximum number of computations

required is lesser than the total time available to the

agent. In practice, this turns out be overly conserva-

tive and wasteful. This is because the caching scheme

works really well in practice resulting in actual run-

times being much lower with memoization that with-

out. Obtaining a theoretical characterization of the

beneﬁts of memoization would pave the way to real-

izing bounded rationality for this problem in a con-

tractual environment.

In the meanwhile, bounded rationality may be re-

alized by the following simple and straightforward

anytime algorithm. First, start with a coarse dis-

cretization and compute the optimal schedule (clearly,

this will be fast but will output poor results). Then,

make the discretization ﬁner and recompute a better

schedule. This is repeated until time runs out or the

agent is interrupted – at which point the most recent

fully computed result is available.

5.2.3 Empirical Results and Discussion

We consider an L2-Seller Ann who believes that the

buyer is from one of three type classes – two L0-

Buyer classes with mpd values of 0.1 and 0.2 respec-

tively, and an L1-Buyer class which believes that the

seller is uniformly one of three types – L0-Seller(1d),

L0-Seller(3d) or L0-Seller(1dr).

We solve Ann’s model using the memoized top-

down approach for various settings of the discretiza-

tion resolution and horizon. The computations were

done on a Pentium 4 3.2GHz, 1GB RAM machine.

The results are indexed and presnted in Table 4 ac-

cording to the column index legend in Table 3. We

observe the following:

Memoization Enhancement. The number of actual

(explicit) computations performed is lesser than the

total possible number of computations by many or-

ders of magnitude.

Bounded Rationality through Fine-tuning Action

Space Discretization. The expected proﬁt is greater

for ﬁner discretizations than for coarser ones. The

running time is also greater for ﬁner discretizations.

Therefore, quality of the solution increases with a

ﬁner resolution of the action space, while correspond-

ing simultaneously to an increase in the running time.

In addition, we also observed that the inﬁnite hori-

zon case takes considerably lesser time than the ﬁ-

nite horizon case. This is not surprising considering

the fact that in the inﬁnite horizon case, the time-to-

horizon (inﬁnity) is always the same at every node

and this increases the likelihood that many more be-

lief states would be repeated than the ﬁnite horizon

case where the time-to-horizon also characterizes the

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

224

belief state. Also, as expected, larger ﬁnite horizon

settings take longer than shorter ones.

6 CONCLUSIONS

In this paper, we considered the problem of seller-

offers bilateral bargaining – an instance of the more

general problem of optimal sequential planning under

uncertainty in multiagent settings. Our main contribu-

tion consisted of developing a boundedly rational ap-

proach for the seller’s problem of generating optimal

offer schedules. The approach is based on achieving

a tradeoff between speed and solution quality by us-

ing the discretization of the action space to ﬁne-tune

the size of the search space of available policies – a

ﬁner resolution leads to better policies (in expecta-

tion) but takes longer to compute, and vice versa. We

also demonstrated how memoization may be used to

exploit redundancies in belief space deliberation. Fur-

ther, we also presented a natural way of avoiding the

problem of model extinction (for e.g. for the buyer

agent, as here) – by maintaining one random model

that explains any action not already accounted for by

other sophisticated models.

The work presented in this paper falls more gen-

erally under the recently formalized paradigm of

decision-theoretic reasoning augmentedwith ﬁnite in-

teractive belief hierarchies. We believe that the results

provided in this paper serve two purposes. Firstly,

it sets forth a principled prescription for achieving

resource bounded rational behavior in bilateral bar-

gaining. Detailed comparative studies of behavioral

economics literature are required to understand if this

model also provides a descriptive account of actual

human behavior in bargaining settings, although this

is only of secondary interest to us. And secondly,

the speciﬁc insights gained – namely, bounded ratio-

nality through ﬁne-tuning the resolution of the action

space to exploit the resultant speed-optimality trade-

off, caching during deliberation and maintaining en-

semble models to avoid model extinction – are gener-

ally applicable to other optimal sequential multiagent

planning problems under uncertainty.

REFERENCES

Aumann, R. and Brandenburger, A. (1995). Epistemic

conditions for nash equilibrium. Econometrica,

63(5):1161–1180.

Cho, I.-K. (1990). Uncertainty and delay in bargaining. Re-

view of Economic Studies, 57(4):575–95.

Cramton, P. C. (1984). Bargaining with incomplete infor-

mation: An inﬁnite-horizon model with two-sided un-

certainty. Review of Economic Studies, 51(4):579–93.

Doshi, P. and Gmytrasiewicz, P. (2005). Approximating

state estimation in multiagent settings using particle

ﬁlters. In Proceedings of the Fourth International

Joint Conference on Autonomous Agents and Multi-

agent Systems.

Fudenberg, D. and Tirole, J. (1983). Sequential bargain-

ing with incomplete information. Review of Economic

Studies, 50(2):221–47.

Gmytrasiewicz, P. and Doshi, P. (2005). A framework for

sequential planning in multi-agent settings. Journal of

Artiﬁcial Intelligence Research, 24:49–79.

Grossman, S. J. and Perry, M. (1986). Sequential bargaining

under asymmetric information. Journal of Economic

Theory, 39(1):120–154.

Harsanyi, J. C. (1968). Games with incomplete informa-

tion played by ’bayesian’ players, i-iii. Management

Science, 14:pp. 159–182, 320–334, 486–502.

Kaelbling, L. P., Littman, M. L., and Cassandra, A. R.

(1998). Planning and acting in partially observable

stochastic domains. Artiﬁcial Intelligence, 101:99–

134.

Kalai, E. and Lehrer, E. (1993). Rational learning leads to

nash equilibrium. Econometrica, 61(5):1019–45.

Lovejoy, W. (1991). A survey of algorithmic meth-

ods for partially observed markov decision pro-

cesses. Annals of Operations Research, 28:47–65.

10.1007/BF02055574.

Perry, M. (1986). An example of price formation in bilat-

eral situations: A bargaining model with incomplete

information. Econometrica, 54(2):pp. 313–321.

Rubinstein, A. (1982). Perfect equilibrium in a bargaining

model. Econometrica, 50(1):97–109.

Rubinstein, A. (1985). A bargaining model with incom-

plete information about time preferences. Economet-

rica, 53(5):1151–72.

Sobel, J. and Takahashi, I. (1983). A multistage model of

bargaining. Review of Economic Studies, 50(3):411–

426.

Varkey, P. (2010). Bounded rational decision theoretic bar-

gaining using ﬁnite interactive epistemologies (tech-

nical report). http://www.cs.uic.edu/∼pvarkey.

Zamir, S. (2008). Bayesian games: Games with incomplete

information. Discussion Paper Series dp486, Center

for Rationality and Interactive Decision Theory, He-

brew University, Jerusalem.

RESOURCE BOUNDED DECISION-THEORETIC BARGAINING WITH FINITE INTERACTIVE EPISTEMOLOGIES

225