THE MULTI-AGENT PLANNING PROBLEM

Tam´as Kalm´ar-Nagy

Department of Aerospace Engineering, Texas A&M University, College Station, TX 77845, U.S.A.

Giovanni Giardini

Gemelli S.p.A., Canegrate, Milano, Italy

Keywords:

Multiple traveling salesman problem, Genetic algorithm.

Abstract:

The purpose of this paper is to present a Multi-Agent planner for a team of autonomous agents. The approach

is demonstrated by the Multi-Agent Planning Problem, which is a variant of the classical Multiple Traveling

Salesmen Problem (MTSP): given a set of n goals/targets and a team of m agents, the optimal team strategy

consists of ﬁnding m tours such that each target is visited only once and by only one agent, and the total cost of

visiting all nodes is minimal. The proposed solution method is a Genetic Algorithm Inspired Steepest Descent

(GAISD) method. To validate the approach, the method has been benchmarked against MTSPs and routing

problems. Numerical experiments demonstrate the goodness of the approach.

1 INTRODUCTION

Improving the capability of a system to plan and

to act autonomously represents an important direc-

tion in the ﬁeld of autonomy and artiﬁcial intelli-

gence. Many applications, from space exploration

(http://marsrovers.nasa.gov, ; Hayati et al., 1997;

Baumgartner, 2000) to search and rescue problems

(Birk and Carpin, 2006; Sariel and Akin, 2005; Ja-

coff et al., 2002; Carpin et al., 2006), have underlined

the need for autonomous systems that are able to plan

strategies either with or without human feedback.

However, many ‘autonomous’ vehicles are pro-

vided with no decision or planning capability. They

are typically able to execute given commands (i.e.

reaching a particular point or using a required instru-

ment), but they are not able to decide by themselves a

sequence of tasks or a plan to achieve. Mission strat-

egy and the goals to accomplish are usually decided

by human operators.

Our long-term goal is to realize a multi-agent

planner for a team of autonomous vehicles to co-

operatively explore their environment (Giardini and

Kalm´ar-Nagy, 2007). To achieve this goal, we re-

quire that the vehicles/agents be able to compute a

coordinated mission strategy. Speciﬁcally, the overall

planning problem can be formulated as ﬁnding a near-

optimal set of paths that allows the team of agents to

visit a given number of targets in the shortest amount

of time.

This problem is quite similar to the well-known

Multiple Traveling Salesmen Problem (MTSP)

(Mitrovic-Minic and Krishnamutri, 2002; Bektas,

2006; Hong and Padberg, 1977; Singh and Baghel,

2009), a generalization of the Traveling Salesman

Problem (TSP) (Johnson and McGeoch, 1997;

http://www.tsp.gatech.edu/, ; Gutin and Punnen,

2002) that can be stated as follow:

Given n nodes (targets) and m salesmen (agents)

located at the same node (the depot), the MTSP

consists of ﬁnding m closed tours (that start and end

at the depot), such that each target is visited only

once and by only one agent and the total cost of

visiting all nodes is minimal.

MTSP has been used for modeling many real sit-

uations, from scheduling activities of companies and

industries to cooperative planning problems. See for

example (Carter and Ragsdale, 2002), where MTSP

is used for modeling the pre-printed insert schedul-

ing problem. Planning problems have also been in-

vestigated through MTSP formulations, speciﬁcally

in (Stentz and Brummit, 1998; Stentz and Brummit,

1996), where a dynamic mission planning system for

multiple mobile robots operating in unstructured en-

vironments is presented (analysis of planetary explo-

ration), or in (Yu et al., 2002), where the MTSP for-

296

Kalmár-Nagy T. and Giardini G..

THE MULTI-AGENT PLANNING PROBLEM.

DOI: 10.5220/0003177502960305

In Proceedings of the 3rd International Conference on Agents and Artiﬁcial Intelligence (ICAART-2011), pages 296-305

ISBN: 978-989-8425-40-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

mulation is used to describe a path planning problem

for a team of cooperative vehicles.

An important and well-studied extension

of the MTSP is the Vehicle Routing Problem

(http://neo.lcc.uma.es/radi aeb/WebVRP/, ; Pereira

et al., 2002), where a ﬂeet of vehicles of different

capacities, based at either one or several depots,

must deliver different customer demands (the number

of vehicles is often considered as a minimization

criterion in addition to total traveled distance).

In this work, the problem of planning a set of

strategies for cooperatively exploring the environ-

ment with a ﬂeet of vehicles is modeled as a variant

of the classical MTSP, referred to as the Multi-Agent

Planning Problem (MAPP):

Given n nodes (targets) and m salesmen (agents)

located at different depots, the MAPP consists of

ﬁnding m tours such that each target is visited only

once and by only one agent, while minimizing a given

cost function.

Here we present a multi-agent planner for obtain-

ing good quality MAPP solutions. The method is

based on a Genetic Algorithm Inspired Steepest De-

scent method, simply called GAISD.

The paper is organizedas follows: after the MAPP

formulation(Section 2), and an overviewof howsimi-

lar problems (MTSP above all) are solved (Section 3),

the proposed GA-Inspired Steepest Descent method

is described in Section 4. Results are then reported in

Section 5, conclusions in Section 6.

2 MAPP FORMULATION

Graph theory has been instrumental for analyzing and

solving problems in areas as diverse as computer net-

work design, urban planning, and molecular biol-

ogy. Highly regarded books on graph theory include

(Bondy and Murty, 1976; Diestel, 2005).

In this Section we deﬁne the problem of comput-

ing an optimal strategy for a team of agents to visit a

set of known targets.

Let T = {t

, . . . ,t

} be the set of n targets (goals)

to be visited. The i-th target t

is an object located

in Euclidean space and its position is speciﬁed by the

vector r(t

). Let A = {a

, . . . , a

} denote the set of m

agents, each one speciﬁed by the r(a

) in Euclidean

space.

For the i-th agent, the augmented vertex set is

given by V

= T ∪ a

and the conﬁguration space of

the problem is the complete graph K

n+1

The weight associated with each edge is given by

the Euclidean distance between the corresponding lo-

cations, i.e. w(v

, v

) = w(v

, v

) =k r(v

) − r(v

) k,

with v

, v

∈ V, rendering K

n+1

) a weighted and

symmetric graph.

Let P

denote a path of length k

starting at vertex

, the Multi-Agent Planning Problem is equivalent to

ﬁnding a set of m pairwise disjoint paths P

P = {P

, . . . , P

∑

i=1

= n, (1)

such that the length of the longest path

(P) = max

W (P

) (2)

is minimal (this is the so-called minmax problem). In

other words, m agents have to visit n targets in the

least amount of time, with the constraint that every

target is only visited once. Note that the agents all

have different starting positions (paths are pairwise

disjoint) and can visit a different number of targets

(no constraints are imposed on the path lengths k

The Multi-Agent Planning Problem is a variant of

the classical Multiple Traveling Salesman Problem,

that can be formulated as follows. Let T = {t

, . . . , t

}

be the set of n targets to be visited and let a denote

the unique depot the m agents share. The augmented

vertex set is given by V = T ∪ a and the conﬁguration

space of the problem is the complete graph K

n+1

(V).

Let C

denote a cycle of length k

starting and end-

ing at vertex a (the depot). The Multiple Traveling

Salesmen Problem can be formulated as ﬁnding m cy-

cles C

of length k

C = {C

, . . . ,C

∑

i=1

= n + m, (3)

such that each target is visited only once and by only

one agent and the sum of the costs of all the m tours

W (C) =

∑

i=1

W (C

) (4)

is minimal.

3 OVERVIEW OF SOLUTION

METHODS

The obvious difﬁculty with the Multiple Traveling

Salesman Problem and consequently the Multi-Agent

Planning Problem is their combinatorial nature (they

are NP-hard, and there is no known deterministic al-

gorithm that solves them in polynomial time).

A common approach is to transform the studied

THE MULTI-AGENT PLANNING PROBLEM

297

MTSP into an equivalent Traveling Salesman Prob-

lem, for which solutions can be found by applying

both well-known exact methods (e.g. branch-and-

bound algorithms and linear programming (Tschoke

et al., 1995; Balas and Toth, 1985; Schrijver, 1986))

and approximate algorithms such as Genetic Algo-

rithms, Simulated Annealing and Ant System (Carter,

2003; Kulich et al., 2004). For example, in (Goren-

stein, 1970; Tang et al., 2000) the authors proposed to

transform the MTSP into an equivalent TSP by adding

dummy cities and edges with ad-hoc null or inﬁnite

costs. However, as stated in (Gavish and Srikanth,

1986; Junjie and Dingwei, 2006; Kara and Bektas,

2006), transforming the MTSP into an equivalentTSP

can result in a harder problem to solve (i.e. the equiv-

alent TSP can be more arduous than solving an or-

dinary TSP). Similar approaches are investigated in

(Singh and Baghel, 2009; Orloff, 1974; Bellmore and

Hong, 1974).

The ﬁrst attempt to solve large-scale MTSPs is

given in (Gavish and Srikanth, 1986), where a branch-

and-bound method (the most widely adopted tech-

nique for solving these combinatorial problems (La-

porte et al., 1987)) is applied to both Euclidean (up to

100 cities and 10 salesmen) and non Euclidean prob-

lems (up to 500 cities and 10 salesmen). Branch-and-

bound is also applied in (Ali and Kennington, 1986)

for solving an asymmetric MTSP up to 100 cities.

Other solution methods have also been pro-

posed, from simulated annealing (Stentz and Brum-

mit, 1998) (here coupled with a general-purpose in-

terpreted grammar) to evolutionary algorithms (i.e. in

(Sofge et al., 2002), different evolutionaryalgorithms,

ranging from Genetic Algorithms to Particle Swarm

and Monte-Carlo optimization, are compared). In

(Junjie and Dingwei, 2006) the MTSP with ability

constraint is solved with an Ant Colony Optimiza-

tion (ACO) algorithm, where the MTSP is not trans-

lated into an equivalent TSP and the ACO algorithm

is opportunely modiﬁed for dealing with the charac-

teristics of the original problem (the MTSP). In (Jun-

jie and Dingwei, 2006) results are compared with a

modiﬁed Genetic Algorithm, that solves the equiv-

alent TSP. In (Kara and Bektas, 2006), Linear Pro-

gramming is used, and similar to (Junjie and Dingwei,

2006), the original MTSP is analyzed and solved (no

TSP translation). In both (Kara and Bektas, 2006) and

(Junjie and Dingwei, 2006), the authors conclude that

the original MTSP is easier to solve than the derived

TSP.

An important work is (Na, 2006), where different

local search heuristics are presented and compared.

In (Carter and Ragsdale, 2002; Carter and Rags-

dale, 2006; Carter, 2003; Brown et al., 2007), Genetic

Algorithms are used, and the sum of the salesmen

path lengths is minimized, as is the maximum dis-

tance traveled by each salesmen (to balance the agent

workload). (Tang et al., 2000) uses a modiﬁed Ge-

netic Algorithm on the equivalent TSP.

4 MAPP: PROPOSED METHOD

Given m ≥ 1 agents and n known targets/cities to visit,

the optimal team strategy (also called Team Plan), is

sought that allows the ﬂeet to visit every target only

once.

We represent the Team Plan as a collection of m

distinct subtours. Thus, given m agents and n targets,

Team Plan P is deﬁned as P = {P

, . . . , P

}, where

is the path of the i-th agent visiting k

< n tar-

gets. Note that this representation allows the individ-

ual subtours to have different lengths. Moreover, the

Multi-Agent Planning Problem can also be rewritten

for each i-th agent to ﬁnd the best possible Subtour of

length k

< n that satisﬁes the imposed cost function.

The proposed optimization technique is a Ge-

netic Algorithm Inspired Steepest Descent (GAISD)

method. Brieﬂy, a Genetic Algorithm (GA) is an opti-

mization technique used to ﬁnd approximatesolutions

of optimization and search problems. Genetic Al-

gorithms are a particular class of evolutionary meth-

ods that use techniques inspired by Darwin’s theory

of evolution and evolutionary biology, such as inher-

itance, mutation, selection, and crossover. In these

systems, populations of solutions compete and only

the ﬁttest survive.

Similar to the classical GA, GAISD consists of

two phases: initialization and evolution. In the initial-

ization phase, the starting Team Plan is created (see

Section 4.1), while the evolution phase (see Section

4.2) evolves it toward a near-optimal ﬁnal solution.

4.1 Initialization Phase

During the initialization phase, the starting Team Plan

is created, and thus the starting set of subtours is

planned. The initialization phase is an important

step in the optimization process, since it deﬁnes the

starting point for the evolutionary search, and conse-

quently the effectiveness of the algorithm.

Let T

= {t

, . . . , t

} and A = {a

, . . . , a

} be the

set of n targets and the m agents, respectively. The

initial Team Plan is created in a sequential order, and,

without loss of generality, we assume that the order of

planning is a

, a

, . . . , a

and that the starting subtours

have similar lengths. For feasible plans, subtours that

are pairwise disjoint need to be created.

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

298

(a) Random selection. (b) Deterministic selection.

Figure 1: Crossover operator: two subtours are randomly (a) or deterministically (b) selected and mated through the crossover

operator. In the deterministic case, the best and the worst subtours are selected.

As a ﬁrst step, a Subtour P

of length k

is com-

puted. At the end of the a

initialization phase, agent

plans its own Subtour P

considering a target set

that is simply obtained by discarding from T

the

targets visited by agent a

. In general, the i-th agent

plans a Subtour P

on the targets not yet allocated by

the previous agents. Obviously, this process yields a

feasible Team Plan P = {P

, . . . , P

Based on this mathematical formulation, two ini-

tialization methods are proposed:

• Greedy Initialization: the initial Team Plan is

created using a greedy approach to form feasible

starting subtours. Each agent selects the targets to

visit following a Nearest Neighbor method: given

a target i, target i+ 1 is the nearest not yet visited

one.

• TSP-based Initialization: for those problems

where the positions of the m agent are not imposed

(the m agents can start from any target t

∈ T), a

feasible starting Team Plan P = {P

, . . . , P

} can

be generated by clustering the TSP solution com-

puted on the complete graph K

(T). ‘Clustering’

is carried out by discarding m edges from the TSP

tour, in order to ‘equally’ subdivide it, and having

m starting subtourswith similar costs. This initial-

ization method introduces a degree of complexity

in the overall system, since a TSP solution must

be computed.

4.2 Evolution Phase

The evolution phase evolves the Team Plan, trying to

design a strategy where the mission time is reduced

(minimizing the cost W

(P), see cost function (2)).

This phase has the same mechanism of a classical

Genetic Algorithm (Goldberg, 1989) while introduc-

ing an important difference: only one Team Plan P,

not a population of them, is evolved.

At every evolution/generation step, a set of op-

erators (see Section 4.3) is applied to the subtours

∈ P, either improving the Team Plan or not. If P

improves, it is used at the next generation step, oth-

erwise the Team Plan before the application of the

operators is restored. No elitism is considered, and

the unique Team Plan changes only when its cost de-

creases (Steepest Descent). An evaluation phase eval-

uates, at each generation step, the Team Plan.

The logical ﬂowchart of the GAISD evolution

phase is shown in Figure 2.

4.3 Team Plan Operators

The evolution of the unique solution P toward a near-

optimal multi-agent strategy is accomplished by com-

bining the genetic materials of its subtours through

the application of genetic-like operators.

Three different operators have been designed: the

crossover, the mutation and the migration. The oper-

ators are applied in a predeﬁned order, and their ap-

plication depends on a given probability, as shown in

Figure 2. In addition to these operators, the heuristic

2-opt method (Matayoshi et al., 2004; Bentley, 1990;

Sengoku and Yoshihara, 1998) to directly improvethe

goodness of the single agent plans is introduced (it re-

places subtours with better ones from their ‘neighbor-

hood’).

The Crossover Operator combines the genetic

materials of two selected subtours(called parents), re-

placing them with the two newly created ones (called

offspring). At every generation step the crossover op-

erator is applied only once, thus only two subtours are

chosen and mated. Depending on a given probability

selection

), parents can be chosen either randomly (see

Figure 1(a)) or deterministically (see Figure 1(b)). In

the deterministic case, the mating process always oc-

curs between the subtours with maximum and min-

imum costs. Once selected, parents are mated in a

classical way (Goldberg, 1989): they are randomly

halved (not necessarily at the same target) and their

halves are simply swapped.

The Mutation Operator changes the Team Plan by

randomly swapping two genes between two different

subtours. The Migration Operator consists of moving

a randomly chosen target from a Subtour P

∈ P (of

length k

) to a Subtour P

∈ P (of length k

). Note that

the lengths of the subtours change: k

decreases while

increases.

THE MULTI-AGENT PLANNING PROBLEM

299

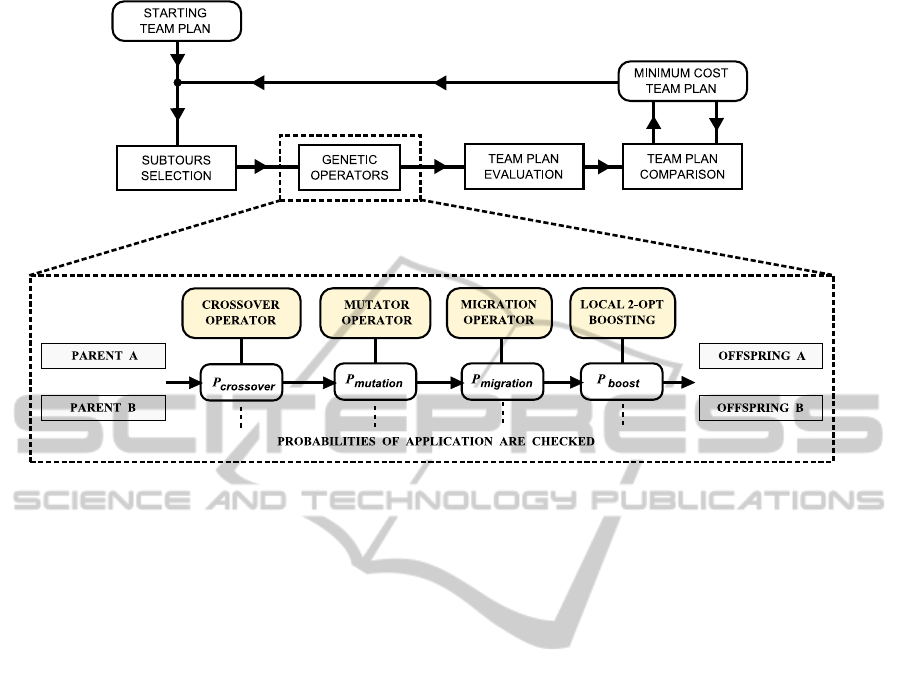
Figure 2: Flowchart of the evolution phase, together with the sequence of operators.

With probability p

boost

, each Subtour is processed

with a heuristic boosting technique. The local search

method adopted here is the 2-opt method (Matayoshi

et al., 2004; Bentley, 1990; Sengoku and Yoshihara,

1998) that replaces solutions with better ones from

their ‘neighborhood’.

Let us consider a set T of n targets and the cor-

responding complete and weighted graph K

n+1

(V)

(V = T ∪ a with a being the agent). Let P denote the

considered Subtour, with 1 ≤ k ≤ n, coded as a se-

quence of targets s = (x

, . . . , x

) (where x

∈ T). The

2-opt method determines whether the inequality

w(x

, x

i+1

) + w(x

, x

j+1

) > w(x

, x

) + w(x

i+1

, x

j+1

)

between the four vertices x

, x

i+1

, x

and x

j+1

of P

holds, in which case edges (x

, x

i+1

) and (x

, x

j+1

) are

replaced with the edges (x

, x

) and (x

i+1

, x

j+1

), re-

spectively. This method provides a shorter path with-

out intersecting edges.

5 RESULTS

An extensive set of simulations were run to test the

performance of the proposed method. Where neces-

sary, for the possibility of comparing our results with

other referenced ones, some constraints have been in-

troduced.

Unless otherwise speciﬁed, simulations were run

for 150000 generation steps, while the crossover,

mutation, migration and boosting (2-opt) operators

were applied with a p

crossover

= 70%, p

mutation

40%, p

migration

= 60% and p

boost

= 30%, respec-

tively. When the crossover operator is applied, the

probability of deterministically selecting two parents

is equal to p

selection

= 50%.

For each simulation, the initialization method is

always speciﬁed, and can be either the greedy or the

TSP-based one.

5.1 Comparison with Structured and

Well-known Solutions

In this Section, GAISD has been compared with

known literature results. In order to make the com-

parison meaningful, we introduce, where necessary,

the same constraints adopted in the referenced works.

5.1.1 Comparison with Evolutionary Algorithms

We compare our method with the results reported in

(Junjie and Dingwei, 2006), where an Ant Colony

Optimization algorithm is compared against the Mod-

iﬁed Genetic Algorithm (MGA) described in (Tang

et al., 2000). Six MTSPs, all derived from well-

known TSPLIB instances (Reinelt, 1991), are solved.

The number of agents is ﬁxed, m = 5, and they all

share the same starting location (that is, the ﬁrst tar-

get in the corresponding problem data ﬁle). In addi-

tion, the maximum length of the cycles, k

max

, is lim-

ited (note that since MTSPs are considered here, we

need to ‘modify’ the Team Plan using cycles instead

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

300

of paths).

In both (Junjie and Dingwei, 2006; Tang et al.,

2000), rounded costs are considered. Therefore, for

meaningful comparison, we need to minimize the fol-

lowing cost function:

W (C) =

∑

i=1

round (W (C

)). (5)

Finally, since a single depot is considered, only the

greedy initialization method is used.

Results are shown in Table 1, and they are based

on an average of 100 simulations. In this case, the ob-

tained results globally outperform the literature ones.

Figure 3 shows also the solution obtained for the pr76

TSPLIB problem.

0 5000 10000 15000 20000

2000

4000

6000

8000

10000

12000

14000

X COORDINATE

Y COORDINATE

(a) pr76 TSPLIB problem: starting Team Plan.

0 5000 10000 15000 20000

2000

4000

6000

8000

10000

12000

14000

X COORDINATE

Y COORDINATE

(b) pr76 TSPLIB problem: ﬁnal Team Plan.

Figure 3: The pr76 TSPLIB target conﬁguration is here

adopted, and the MTSP is solved. The maximum plan

length is constrained to k

max

= 20 targets and m = 5 agents

are considered. Cost function (5) is minimized, and the

comparison between the starting and the ﬁnal Team Plans

is shown. In (a) the starting Team Plan, with cost equal to

194618, is shown, while in (b) the ﬁnal TeamPlan, with cost

equal to 152722, is reported. This solution is 15.4% and

2.6% better than the referenced ones, obtained by imple-

menting an Ant Colony Optimization method and a Modi-

ﬁed Genetic Algorithm, respectively.

5.1.2 Comparison with Heuristics

We compare our method against the results reported

in (Na, 2006), where different heuristics methods are

proposed and compared for solving MTSP instances.

In (Na, 2006), a no-depot MTSP variant is consid-

ered (the agents do not have a predeﬁned starting loca-

tion), and the minmax optimization problem is solved

(cost function (2) is minimized). In addition, the num-

ber of salesmen is ﬁxed and no constraints on the plan

lengths are imposed. Note that since we are compar-

ing our method with MTSP results, we need to mod-

ify our Team Plan accordingly, using cycles instead

of paths. In addition, since in (Na, 2006) rounded

distances are considered, for meaningful comparison

cost function (2) is opportunely modiﬁed:

round (W (C

)). (6)

For each test case, our results are compared with only

the best ones of (Na, 2006), without considering all

the other (worse) solutions. We also report the name

of the Heuristic with which each referenced solu-

tion has been obtained (please refer to (Na, 2006) for

a more detailed description of the adopted heuristic

methods). Tables 2 and 3 show the results obtained

by initializing the Team Plan either with the greedy

or the TSP-based initialization methods, respectively.

Results are averaged over 100 simulations.

In each test case, GAISD returns good solutions,

independent of the applied initialization method. In

general, our best solutions are closer to the litera-

ture ones, and, in a few cases (for example in the

berlin52 or the pr264 problems), even better. The

greedy initialization method seems to better initial-

ize the Team Plan in those problems where the dis-

tribution of targets has a well deﬁned structure (the

pr264 problem), while in ‘small-size’ problems (i.e.

berlin52) the TSP-based method is preferable (even if

the obtained improvementdoes not justify its required

complexity, time and computational costs).

Figure 4 shows the solutions obtained by applying

the greedy (Figure 4 (a)) and the TSP-based (Figure

4 (b)) initialization methods for the kroA100 problem

(with m = 5 agents). In this case, if compared with

(Na, 2006), the TSP-based method and the greedy

method allow for ﬁnal solutions that are only 3.6%

and 7.2% worse than the cited one, respectively.

5.2 Comparison with Other Software

In this Section we test GAISD against a Mat-

lab MTSP solver, based on a Genetic Algorithm

(www.mathworks.com/matlabcentral/ﬁleexchange/,

2008) freely available online.

THE MULTI-AGENT PLANNING PROBLEM

301

Table 1: Comparison between the proposed method and the Ant Colony Optimization (ACO) and the Modiﬁed Genetic

Algorithm (MGA) methods. Results are averaged over 100 simulations. The number of targets can be easily derived from the

TSPLIB problem name. k

max

is the maximum number of targets an agent can visit. For each case, a ﬁxed number of m = 5

agents is considered. Only the greedy initialization method is used (one-depot problem).

TSPLIB

max

ACO MGA Proposed Method Difference of Means

Problem Min Mean Min Mean Min Mean ACO MGA

pr76 20 178597 180690 157444 160574 152722 156503.9 −15.4% −2.6%

pr152 40 130953 136341 127839 133337 114698 126128.8 −8% −5.7%

pr226 50 167646 170877 166827 178501 152198 158073.9 −8% −12.9%

pr299 70 82106 83845 82176 85796 70059 71705.1 −16.9% −19.6%

pr439 100 161955 165035 173839 183698 136169 138655.5 −15.6% −24.5%

pr1002 220 382198 387205 427269 459179 311492 319240.4 −17.5% −30.5%

Table 2: Heuristic comparison: for each case, 100 simulations have been run. The initialization phase is based on the greedy

method. The number of targets can easily be derived from the TSPLIB problem name.

TSPLIB Number of Heuristics Greedy Method Errors

Problem Agents Method Minimum Mean Minimum Mean Minimum Mean

berlin52

4 bisection 2182 2204.3 2183 2422.4 0.04% 9.8%

5 k-split 1713 1739.7 1825 2160.4 6.5% 24.2%

SGH 1531 1585

1611 1905.8

- 20.2%

bisection 1476 1643.1 9.1% -

kroA100

4 SGH 5955 6096.7 6000 6690.3 0.7% 9.7%

5 k-split 4629 5025.9 4964 5620.1 7.2% 11.8%

k-center 4200 4429.4

4370 5038.4

4% -

k-means 4230 4234.6 - 18.9%

bier127

4 bisection 32423 32757.5 32434 35740.9 0.03% 9.1%

6 k-split 22815 23071.7 24608 26993.3 7.8% 16.9%

pr264

4 bisection 12705 12705 12196 13830.3 −4.1% 8.8%

k-means 8526 9131.6

9000 10256.3

5.5% -

bisection 8739 9051.6 - 13.3%

Table 3: Heuristic comparison: for each case, 100 simulations have been run. The initialization phase is based on the TSP-

based method. The number of targets can easily be derived from the TSPLIB problem name.

TSPLIB Number of Heuristics TSP-based Method Errors

Problem Agents Method Minimum Mean Minimum Mean Minimum Mean

berlin52

4 bisection 2182 2204.3 2088 2359.6 −4.5% 7%

5 k-split 1713 1739.7 1804 2014.8 5.3% 15.8%

SGH 1531 1585

1576 1801.2

- 13.6%

bisection 1476 1643.1 6.7% -

kroA100

4 SGH 5955 6096.7 6000 6443.6 0.7% 5.7%

5 k-split 4629 5025.9 4796 5314.6 3.6% 5.7%

k-center 4200 4429.4

4310 4693.9

2.6% -

k-means 4230 4234.6 - 10.8%

bier127

4 bisection 32423 32757.5 32948 34606 1.6% 5.6%

6 k-split 22815 23071.7 24290 26497.1 6.4% 14.8%

pr264

4 bisection 12705 12705 13400 19135.3 5.4% 50.6%

k-means 8526 9131.6

8629 14395.8

1.2% -

bisection 8739 9051.6 - 59%

The number of agents is ﬁxed, and the minimum

path length, k

min

= 2, is imposed (this way, solutions

with paths composed of only one target are avoided).

Cost function (2) is minimized, and targets are

randomly generated over the unit square map. In

all simulations, the greedy initialization method is

adopted. Since the Matlab MTSP solver is based only

on a Genetic Algorithm, and no heuristics is used, we

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

302

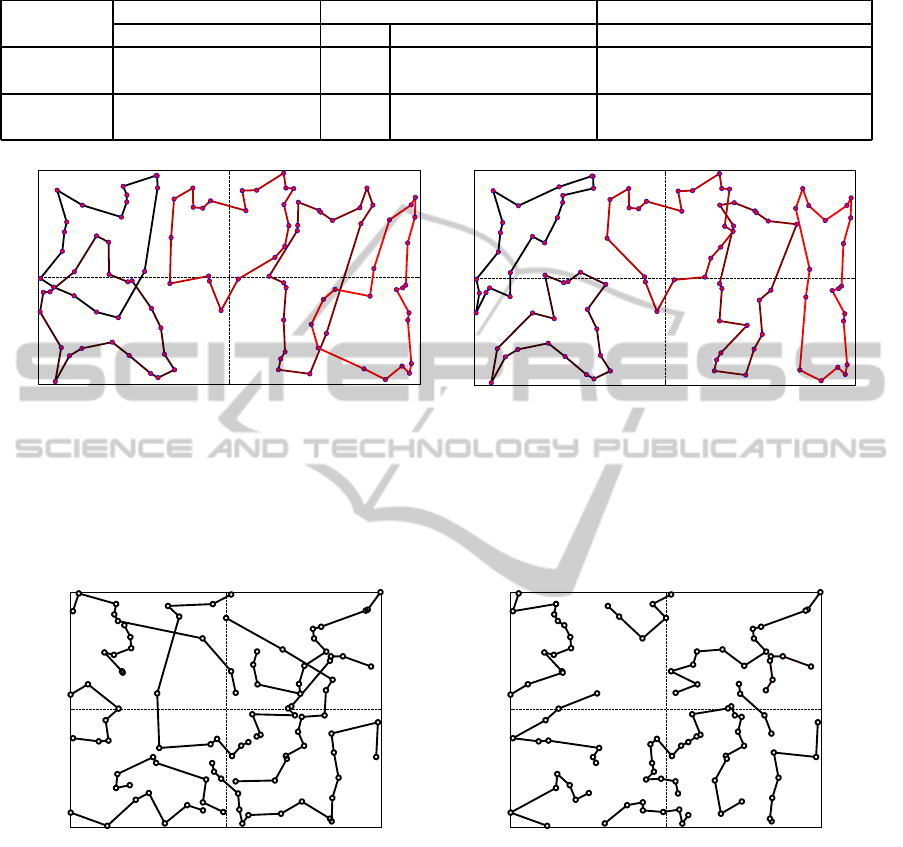
Table 4: Comparison between the proposed method against a Matlab MTSP code. For each test, k

min

= 2 and the greedy

initialization method is used. Targets are randomly generated over the unit square map.

Test case

Matlab Code Proposed Method Cost Variation

Min Mean Max p

boost

Min Mean Max Min Mean Max

100 targets

7.14 8.19 9.21

30% 6.37 6.72 7.11 −10.7% −17.9% −22.8%

10 agents 0% 6.67 7.14 7.58 −6.5% −12.8% −17.7%

200 targets

15.64 17.5 19.65

30% 9.55 9.89 10.25 −39% −43.5% −47.8%

20 agents 0% 10.05 10.6 11.23 −35.7% −39.4% −42.8%

0 2000 4000

1000

2000

X COORDINATE

Y COORDINATE

(a) kroA100 problem: greedy initialization.

0 2000 4000

1000

2000

X COORDINATE

Y COORDINATE

(b) kroA100 problem: TSP-based initialization.

Figure 4: For the same problem, the MTSP has been solved by applying both the greedy and the cluster initialization methods.

In both cases, m = 5 agents are considered, and the target set is the kroA100 TSPLIB one. In (a), the greedy initialization

method is used and the ﬁnal obtained Team Plan is shown. The ﬁnal Team Plan is the best computed one and its cost is equal

to 4964, that is 7.2% worse than the referenced one. In (b), the TSP-based initialization method is used and the obtained ﬁnal

Team Plan is shown. In this case, its cost is equal to 4796, that is only 3.6% worse than the referenced one.

0 0.5 1

0.5

X COORDINATE

Y COORDINATE

(a) Matlab solution.

0 0.5 1

0.5

X COORDINATE

Y COORDINATE

(b) Proposed method.

Figure 5: GAISD has been compared with a Matlab MTSP solver. In this example, MAPP is solved. 100 targets are randomly

distributed over the unit square map. m = 10 agents are considered. The minimum path length is k

min

= 2. Cost function (2)

is minimized. In (a) the solution obtained by running the MTSP Matlab solver is shown, and its cost is W

= 7.92. In (b) our

solution is proposed. In this case, the total cost is W

= 6.37, that is 19.5% better than the MTSP Matlab solver one.

also run a set of tests with p

boost

= 0%.

Table 4 shows the obtained results, averaged over

100 simulations. Our method clearly outperforms the

Matlab one, both with and without the application

of the 2-opt method (clearly, with the 2-opt method

the results are better). Figures 5 shows two examples

where the Matlab MTSP solver solution is compared

with the GAISD ones.

6 CONCLUSIONS AND FUTURE

WORKS

This paper describes the Multi-Agent Planning Prob-

lem, a variant of the classical Multiple Traveling

Salesman Problem where the agents do not have the

constraint of returning to their starting location. The

solution method is based on a simpliﬁed Genetic

THE MULTI-AGENT PLANNING PROBLEM

303

Algorithm, that is initialized in two different ways:

a greedy (Nearest Neighbor) and a TSP-based ap-

proach. The importance of this work is to provide

a team of agents the ability to plan a common set of

strategies, the Team Plan, by sharing in an optimal

way a set of given targets/goals.

The results presented here show the success of the

approach, demonstrating how a simple method can

solve otherwise hard combinatorial problems.

REFERENCES

Ali, A. I. and Kennington, J. L. (1986). The asymmetric m-

traveling salesman problem: a duality based branch-

and-bound algorithm. Discrete Applied Mathematics,

13(2-3):259–276.

Balas, E. and Toth, P. (1985). Branch and bound methods.

In Lawler, E. L., Lenstra, J., Rinnooy Kart, A. H. G.,

and Shmoys, D. B., editors, The Traveling Salesman

Problem, chapter 10, pages 361–397. New York, John

Wiley and Sons edition.

Baumgartner, E. T. (2000). In-situ exploration of Mars us-

ing rover systems. In Proceedings of the AIAA Space

2000 Conference, number 2000-5062, Long Beach,

CA, USA. AIAA.

Bektas, T. (2006). The Multiple Traveling Salesman Prob-

lem: an overview of formulations and solution proce-

dures. Omega (Oxford), 34(3):209–219.

Bellmore, M. and Hong, S. (1974). Transformation of Mul-

tisalesman Problem to the standard Traveling Sales-

man Problem. Journal of the ACM, 21(3):500–504.

Bentley, J. L. (1990). Experiments on Traveling Salesman

heuristics. In Proceedings of the First Annual ACM-

SIAM Symposium on Discrete Algorithms, pages 91–

99, Philadelphia, PA, USA. Society for Industrial and

Applied Mathematics.

Birk, A. and Carpin, S. (2006). Rescue robotics - A crucial

milestone on the road to autonomous systems. Ad-

vanced Robotics, 20(5):595–605.

Bondy, J. and Murty, U. (1976). Graph Theory with appli-

cations. Macmillan London.

Brown, E. C., Ragsdale, C. T., and Carter, A. E. (2007).

A grouping Genetic Algorithm for the Multiple Trav-

eling Salesperson Problem. International Journal

of Information Technology and Decision Making,

6(2):333–347.

Carpin, S., Wang, J., Lewis, M., Birk, A., and Jacoff, A.

(2006). High ﬁdelity tools for rescue robotics: re-

sults and perspectives. RoboCup 2005: Robot Soccer

World Cup IX, 4020:301–311.

Carter, A. E. (2003). Design and application of Genetic Al-

gorithms for the Multiple Traveling Salesperson As-

signment Problem. PhD thesis, Department of Man-

agement Science and Information Technology, Vir-

ginia Polytechnic Institute and State University.

Carter, A. E. and Ragsdale, C. T. (2002). Scheduling pre-

printed newspaper advertising inserts using genetic al-

gorithms. Omega, 30(6):415–421.

Carter, A. E. and Ragsdale, C. T. (2006). A new approach to

solving the Multiple Travelling Salesperson Problem

using Genetic Algorithms. European Journal Opera-

tional Research, 175(1):246–257.

Diestel, R. (2005). Graph Theory. Springer.

Gavish, B. and Srikanth, K. (1986). An optimal solution

method for large-scale Multiple Traveling Salesmen

Problems. Operations Research, 34(5):698–717.

Giardini, G. and Kalm´ar-Nagy, T. (2007). Centralized and

distributed path planning for Multi-Agent exploration.

In AIAA 2007, Conference of Guidance, Navigation

and Control.

Goldberg, D. E. (1989). Genetic Algorithms in search, op-

timization, and machine learning. Addison-Wesley

Professional, Boston, MA, USA.

Gorenstein, S. (1970). Printing Press Scheduling for

Multi-Edition Periodicals. Management Science,

16(6):B373–B383.

Gutin, G. and Punnen, A. (2002). The Traveling Salesman

Problem and its variations, volume 12 of Combina-

torial Optimizations. Kluwer Academic Publishers,

Norwell, MA, Springer edition.

Hayati, S., Volpe, R., Backes, P., Balaram, J., Welch, R.,

Ivlev, R., Tharp, G., Peters, S., Ohm, T., Petras, R.,

and Laubach, S. (1997). The Rocky 7 rover: a Mars

sciencecraft prototype. In IEEE International Confer-

ence on Robotics and Automation, volume 3, pages

2458–2464, Albuquerque.

Hong, S. and Padberg, M. (1977). A note on the Symmet-

ric Multiple Traveling Salesman Problem with ﬁxed

charges. Operations Research, 25(5):871–874.

http://marsrovers.nasa.gov. Mars Exploration Rover mis-

sions.

http://neo.lcc.uma.es/radi aeb/WebVRP/. The VRP Web.

http://www.tsp.gatech.edu/. Traveling Salesman Problem.

Jacoff, A., Messina, E., and Evans, J. (2002). Experi-

ences in deploying test arenas for autonomous mobile

robots. NIST Special Publication, pages 87–94.

Johnson, D. S. and McGeoch, L. A. (1997). The Traveling

Salesman Problem: a case study in local optimization.

Local Search in Combinatorial Optimization, pages

215–310.

Junjie, P. and Dingwei, W. (2006). An Ant Colony Op-

timization Algorithm for Multiple Travelling Sales-

man Problem. In Proceedings of the First Interna-

tional Conference on Innovative Computing, Informa-

tion and Control, pages 210–213, Washington, DC,

USA. IEEE Computer Society.

Kara, I. and Bektas, T. (2006). Integer linear program-

ming formulations of multiple salesman problems and

its variations. European Journal of Operational Re-

search, 174(3):1449–1458.

Kulich, M., Kubalik, J., Klema, J., and Faigl, J. (2004). Res-

cue operation planning by soft computing techniques.

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

304

In IEEE 4th International Conference on Intelligent

Systems Design and Application, pages 103–109, Bu-

dapest, Hungary.

Laporte, G., Nobert, Y., and Taillefer, S. (1987). A branch-

and-bound algorithm for the asymmetrical distance-

constrained vehicle routing problem. Mathematical

Modelling, 9(12):857–868.

Matayoshi, M., Nakamura, M., and Miyagi, H. (2004). A

Genetic Algorithm with the improved 2-opt method.

In IEEE International Conference on Systems, Man

and Cybernetics, volume 4, pages 3652–3658.

Mitrovic-Minic, S. and Krishnamutri, R. (2002). The Multi-

ple Traveling Salesman Problem with Time Windows:

bounds for the minimum number of vehicles. Techni-

cal Report TR 2002-11, FU CS School.

Na, B. (2006). Heuristics for No-depot Multiple Traveling

Salesmen Problem with Minmax Objective. Master’s

thesis, H. Milton School of Industrial and Engineer-

ing, Georgia Institute of Technology, Atlanta, GA.

Orloff, C. S. (1974). Routing a ﬂeet of m vehicles to/from

a central facility. Networks, 4(2):147–162.

Pereira, F., Tavares, J., Machado, P., and Costa, E. (2002).

GVR: a new Genetic Representation for the Vehicle

Routing Problem. Lecture Notes in Computer Science,

pages 95–102.

Reinelt, G. (1991). TSPLIB: a Traveling Salesman Problem

Library. In ORSA Journal on Computing, volume 3,

pages 376–384.

Sariel, S. and Akin, H. (2005). RoboCup 2004: Robot

Soccer World Cup VIII, volume 3276/2005, chapter

A Novel Search Strategy for Autonomous Search and

Rescue Robots, pages 459–466. Springer.

Schrijver, A. (1986). Theory of linear and integer program-

ming. John Wiley and Sons, Inc. New York, NY, USA.

Sengoku, H. and Yoshihara, I. (1998). A fast TSP solver

using GA on JAVA. In Third International Symposium

on Artiﬁcial Life, and Robotics (AROB III’98), pages

283–288.

Singh, A. and Baghel, A. S. (2009). A new grouping genetic

algorithm approach to the Multiple Traveling Sales-

person Problem. Soft Computing - A Fusion of Foun-

dations, Methodologies and Applications, 13(1):95–

101.

Sofge, D., Schultz, A., and Jong, K. D. (2002). Evolution-

ary computational approaches to Solving the Multiple

Traveling Salesman Problem using a neighborhood at-

tractor schema. Application of Evolutionary Comput-

ing, 2279(0302-9743):153–162.

Stentz, A. T. and Brummit, B. (1996). Dynamic mission

planning for multiple mobile robots. In Proceedings

of the IEEE International Conference on Robotics and

Automation.

Stentz, A. T. and Brummit, B. (1998). GRAMMPS: A Gen-

eralized Mission Planner for Multiple Mobile Robots.

In Proceedings of the IEEE International Conference

on Robotics and Automation.

Tang, L., Liu, J., Rong, A., and Yang, Z. (2000). A Multi-

ple Traveling Salesman Problem model for hot rolling

scheduling in Shanghai Baoshan Iron and Steel Com-

plex. European Journal of Operational Research,

124(2):267–282.

Tschoke, S., Luling, R., and Monien, B. (1995). Solv-

ing the Traveling Salesman Problem with a distributed

branch-and-bound algorithm on a 1024 processor net-

work. Proceedings of the 9th International Sympo-

sium on Parallel Processing, pages 182–189.

www.mathworks.com/matlabcentral/ﬁleexchange/ (2008).

Multiple Traveling Salesmen Problem - Genetic Algo-

rithm.

Yu, Z., Jinhai, L., Guochang, G., Rubo, Z., and Haiyan, Y.

(2002). An implementation of evolutionary computa-

tion for path planning of cooperative mobile robots. In

Proceedings of the Fourth World Congress on Intelli-

gent Control and Simulation, volume 3, pages 1798–

1802.

THE MULTI-AGENT PLANNING PROBLEM

305