
SINGLE-WALK PARALLELIZATION OF THE GENETIC
ALGORITHM
Wojciech Bo˙zejko
Wrocław University of Technology, Janiszewskiego 11-17, 50-372 Wrocław, Poland
Mieczysław Wodecki
University of Wrocław, Joliot-Curie 15, 50-383 Wrocław, Poland
Keywords:
Metaheuristics, Parallel computing, Evolutionary algorithm.
Abstract:
This paper aims at presenting theoretical properties which can be used to approximate the theoretical speedup
of parallel genetic algorithms. The most frequently parallelization method employed to genetic algorithm
implements a master-slave model by distributing the most computationally exhausting elements of the algo-
rithm (usually evaluation of the fitness function, i.e. cost function calculation) among a number of processors
(slaves). This master-slave parallelization is regarded as easy in programming, which makes it popular with
practitioners. Additionally, if the master processor keeps the population (and slave processors are used only
as computational units for individuals fitness function evaluation), it explores the solution space in exactly the
same manner as the sequential genetic algorithm. In this case we can say that we analyze the single-walk
parallel genetic algorithm.
1 INTRODUCTION
Metaheuristics based on the local search method can
be presented as processes of a graph searching in
which vertexesconstitute points of the solutions space
and arcs correspond to the neighborhood relation –
they connect vertexes which are neighbors in the so-
lutions space. We will call it neighborhood graph.
For all NP-hard problems the related neighborhood
has an exponential size. Moving on such a graph de-
fines some path (or other: trajectory) in the solutions
space. Parallel metaheuristic algorithms make use of
many processes to parallel generating or searching the
neighborhood graph.
One can define two approaches to parallelization
of the local search process with the relationship to the
number of trajectories which are concurrently gener-
ated in the neighborhood graph:
1. single-walk parallelization (single trajectory):
fine-grainedalgorithms because of the need of fast
communication (the most computational expen-
sive parts of the algorithm are parallelized),
2. multiple-walk parallelization (many trajectories):
coarse-grained algorithms, communication takes
place more rarely, comparing to single-walk par-
allelized algorithms.
These approaches challenge from the algorithm some
requirements of communication and synchronization
frequency, which implies the kind of granularity.
Single-walk parallel metaheuristics are usually fine-
grained algorithms (Bo˙zejko et al., 2010; Bo˙zejko
et al., 2008b), multiple-walk metaheuristics – coarse-
grained (Bo˙zejko et al., 2008a).
1.1 Single-walk Parallel Algorithms
Single walk algorithms go along the single trajectory,
but they can use multithread calculations to the neigh-
borhood decomposition or parallel cost function com-
putation. For example, calculations of the cost func-
tion value for more complicated cases are frequently
equivalent in determining the longest (critical) path in
a graph, as well as maximal or minimal flow.
1.2 Multiple-walk Parallel Algorithms
Algorithms which make use of a multithread
multiple-walk model search concurrently a solution
space by parallel working searching threads. Addi-
tionally, these algorithms can be divided into sub-
586
Bo
˙
zejko W. and Wodecki M..
SINGLE-WALK PARALLELIZATION OF THE GENETIC ALGORITHM.
DOI: 10.5220/0003177805860590
In Proceedings of the 3rd International Conference on Agents and Artificial Intelligence (ICAART-2011), pages 586-590
ISBN: 978-989-8425-40-9
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

classes due to communication among threads (infor-
mation about actual searching state):
1. independent search processes,
2. cooperative search processes.
If the multithread application (i.e. concurrently work-
ing search processes) does not exchange any infor-
mation we can talk about independent processes of
search. However, if information accumulated dur-
ing an exploration of the trajectory is sent to another
searching process and used by it, then we can talk
about cooperative processes (Bo˙zejko et al., 2008a).
We can also come across a mixed model, so-called
semi-independent (Czech, 2002) executing indepen-
dent search processes keeping a number of common
data.
2 THE METHODOLOGY OF
METAHEURISTICS
PARALLELIZATION
The majority of practical artificial intelligence issues,
especially connected with planning and jobs schedul-
ing, belongs to the class of strongly NP-hard prob-
lems, which require complex and time-consuming so-
lution algorithms. Two main approaches are used to
solve these problems: exact methods and metaheuris-
tics. From one side, existing exact algorithms solv-
ing NP-hard problems possess an exponential compu-
tational complexity – in practice they are extremely
time-consuming. From the other side, metaheuris-
tics provide with suboptimal solutions in a reasonable
time, even being applied in real-time systems.
Quality of the best solutions determined by ap-
proximate algorithms depends, in most cases, on the
number of analyzed solutions, therefore on the time
of computations. Time and quality demonstrates op-
posite tendency in the sense that to obtain a better
solution requires significant increase of computations
time. Parallel algorithms construction makes it possi-
ble to increase significantly the number of considered
solutions (in a unit of time) effectively using multi-
processor computing environment.
The process of an optimization algorithm par-
allelization is strongly connected with the solution
space search method used by this algorithm. The
most frequent are the two following approaches: ex-
ploitation (or search intensification) and exploration
(or search diversification) of the solution space. Due
to this classification we can consider major cate-
gories of the metaheuristic class such as: local search
methods (i.e. tabu search TS, simulated anneal-
ing SA, greedy randomized adaptive search proce-
dure GRASP, variable neighborhood search VNS)
and population-based algorithms (i.e. genetic algo-
rithm GA, evolutionary strategies ESs, genetic pro-
gramming GP, scatter search SS, ant colony optimiza-
tion ACO, memetic algorithm MA, estimated dis-
tribution algorithms EDAs). Local search methods
(LSM) start with a single initial solution improving it
in each step by neighborhood searching. LSMs often
find a locally optimal solution – they are focused on
the solution space exploitation. Population-based al-
gorithms (PBAs) use a population of individuals (so-
lutions), which is improved in each generation. It
means that the average goal function of the whole
population usually improves itself – it does not equal
improving of all the individuals. The whole process is
randomized, so these methods are almost always non-
deterministic. We can say that PBAs are focused on
the solution space exploration.
3 POPULATION-BASED
ALGORITHMS
Population-based algorithms (genetic, memetic, par-
ticle swarm optimization, etc.) are well-suited to par-
allelization due to its natural partitioning onto sepa-
rate groups of solutions, which are concurrently pro-
cessed. The method of using population of individu-
als allows us to diversify searching process onto the
whole solution space. On the other hand, using coop-
eration, it is easy to intensify the search after finding
a good region by focusing individuals onto it. Thanks
to its concurrent nature, population-based algorithms
are very handy to parallelize, especially in the inde-
pendent way using multi-start model. Low level par-
allelization is not so easy because special properties
of the considered problem have to be usually used.
3.1 Genetic Algorithm
Genetic Algorithm (GA) method is an iterative tech-
nique that applies stochastic operators on a set of in-
dividuals (population). Each individual of the popu-
lation encodes the complete solution. Starting popu-
lation is usually generated randomly. A GA applies a
recombination operator (crossover) on two solutions
in order to introduce diversity of population. Addi-
tionally, a mutation operator which randomly modi-
fies an individual is applied as the insurance against
stagnation of the search process. Traditionally GAs
were associated with the binary representation of a
solution, however in jobs scheduling area a permu-
tational solution representation is more popular and
useful.
SINGLE-WALK PARALLELIZATION OF THE GENETIC ALGORITHM
587

The performance of population-based algorithms,
such as GAs, is specially improved when running
concurrently. Two strategies of parallelization are
commonly used:
1. computations parallelization, in which operations
allied to each individuals (i.e. goal function or
genetic operators) are performed in parallel, as
well as
2. population parallelization in which the population
is partitioned into different parts which can be
evolved concurrently or exchanged.
We distinguish the following kinds of parallelization
techniques which are usually applied to genetic algo-
rithms:
• Global parallelization. This model is based on the
master-slave type concurrent processes. The cal-
culations of the objective function are distributed
among several slave processors while the main
loop of the genetic algorithm is executed by the
master processor.
• Independent runs. This approach runs several ver-
sions of the same algorithm with different param-
eters on various processors, allowing the paral-
lel method to be more efficient. The independent
runs model can be also considered as the distribu-
tion model without migration.
• Distributed (island) model. This model assumes
that a population is partitioned into smaller sub-
populations (islands), for which sequential or par-
allel GAs (usually with different crossover and
mutation parameters) are executed. The main
characteristic of this model is that individuals
within a particular island can occasionally migrate
to another island.
• Cellular (diffusion) model. In this model the
population is mapped onto neighborhood struc-
ture and individuals may only interact with their
neighbors. The neighborhood topology is usu-
ally taken from the physical processors connec-
tion network, so this is a fine-grained parallelism
where processors hold just a few individuals.
The distribution model is the most common paral-
lelization of parallel GAs since it can be implemented
in distributed-memory MIMD machines, such as clus-
ters and grids. This approach follows to coarse-
grain parallelization (Bo˙zejko and Wodecki, 2006).
Fine-grained parallel implementations of the cellular
(also called diffusion) model are strongly associated
to the machines on which they are executed (Davidor,
1991). Master-slave implementations are available,
also as general frameworks (i.e. ParadisEO of Cahon
et al. (Cahon et al., 2004)).
We present two approaches in this chapter. The
first one, in the Section 4, follows from Cant´u-Paz
(Cant´u-Paz, 2005) and we discuss it briefly. The sec-
ond one, described in the Section 5, constitutes a new
idea of the broadcasting time approximation for the
master-slave parallel genetic algorithm.
4 SEQUENTIAL BROADCASTING
A parallel genetic algorithm based on the master-slave
model consists of two major modules: (1) communi-
cation module, performed chiefly by the master pro-
cessor which broadcasts a part of population among
slave processors, and (2) computations modules, exe-
cuted both on master and slaves, in which evaluation
of the fitness function is performed. We use a nota-
tion, taken from Cant´u-Paz (Cant´u-Paz, 2005). Let
T
c
be a time used to send a portion of data between
two processors, and let T
f
denote the time required
to evaluate one individual. Each of processors, i.e.
both master and slaves, evaluates a fraction of the
population in the time
nT
f
p
, where p is the number of
processors and n is the size of the population. Next,
we assume in this section that the master broadcasts
the data to slaves processors sequentially, as Figure 1
shows. We omit the time consumed by genetic oper-
ators as well as by the mutation (it is usually much
shorter than the time of the fitness function evalua-
tion). We also assume that the part of data assigned
to each processor (i.e. the number of individuals eval-
uated) is the same both for each slave processor, and
for the master processor.
Figure 1: Sequential broadcasting in the master-slave paral-
lel genetic algorithm.
For a sequential model of broadcasting, the paral-
lel running time is given by the equation
T
p
= pT
c
+
nT
f
p
. (1)
Let us check for which p the T
p
is minimal. We de-
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
588
notes this p by p
∗
1
. Calculating
∂T
p
∂p
= 0 we get
T
c
−
nT
f
p
2
= 0, (2)
p = p
∗
1
=
r
nT
f
T
c
, (3)
which provides us with an optimal number of proces-
sors p
∗
1
minimizing the value of the parallel running
time T
p
. Calculating the maximum value of the theo-
retical speedup S
p
we obtain
S
p
=
T
s
T
p
=
nT
f
pT
c
+
nT
f
p
. (4)
Substituting the optimal number of processors p
∗
1
we
have
S
p
∗
1
=
nT
f
p
∗
1
T
c
+
nT
f
p
∗
1
=
nT
f
q
nT
f
T
c
T
c
+
nT
f
r
nT
f
T
c
=
=
nT
f
p
nT
f
T
c
+
r
(nT
f
)
2
nT
f
T
c
=
p
(nT
f
)
2
2
p
nT
f
T
c
=
1
2
r
nT
f
T
c
=
1
2
p
∗
1
,
(5)
which gives us a maximal possible speedup for this
model of the single-walk master-slave parallel genetic
algorithm.
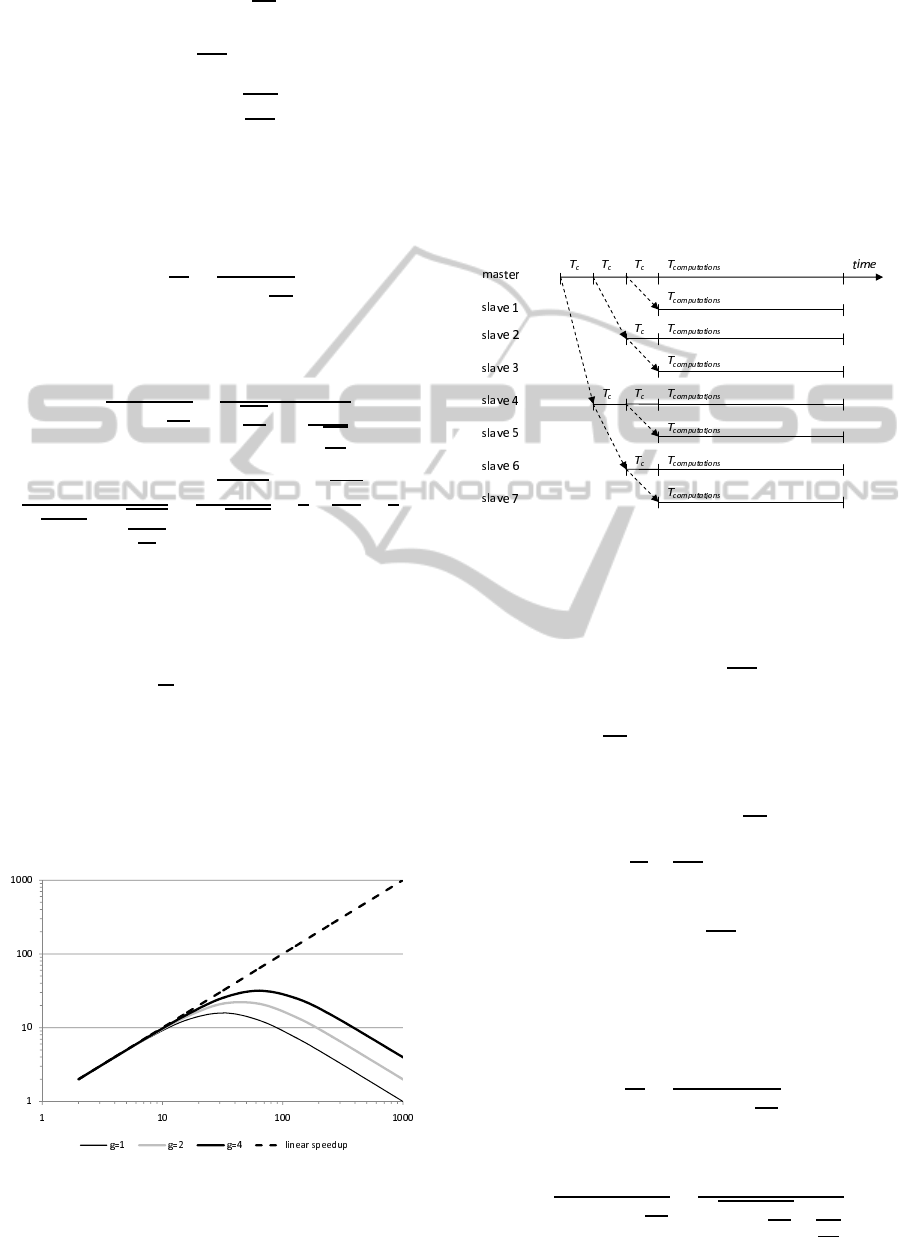
Figure 2 shows possible theoretical speedups for
a given ratio g =
T
f
T
c
. The speedup is plotted for
g = 1, 2, 4 showing that linearity of the speedup in-
creases with g parameter. In practice, T
f
is much
greater than T
c
. In such a situation the parallel algo-
rithm can achieve near-linear speedup for the number
of processors from the range [1, p
∗
1
]. For the num-
ber of processors greater than p
∗
1
speedup quickly de-
creases.
Figure 2: Theoretical speedups for the sequential broad-
casting in the master-slave parallel genetic algorithm.
5 TREE-BASED BROADCASTING
Now, we propose faster model of communication
for the master-slave parallel genetic algorithm. The
broadcasting process is based on tree communication
scheme, which gives us a possibility to obtain loga-
rithmic complexity of the broadcasting process. This
broadcasting scheme needs cooperation of all proces-
sors during the communicationprocess. As scheme of
the master-slave parallel genetic algorithm based on
this communication model is shown on the Figure 3.
Figure 3: Tree-based broadcasting in the master-slave par-
allel genetic algorithm.
For the tree-based communication model the par-
allel running time T
p
is estimated by
T
p
= T
c
log p+
nT
f
p
. (6)
In the case of using more processors, the parallel com-
putations time (
nT
f
p
) decreases, whereas the time of
communication (T
c
log p) increases. We are looking
for such a processors number p (let us call it p
∗
2
) for
which T
p
is minimal. Calculating
∂T
p
∂p
= 0 we obtain
T
c
p
−
nT
f
p
2
= 0 (7)
and then
p = p
∗
2
=
nT
f
T
c
, (8)
which provides us with an optimal number of proces-
sors p
∗
2
which minimizes the value of the parallel run-
ning time T
p
for this model of broadcasting. Calculat-
ing the maximum value of the theoretical speedup S
p
we have
S
p
=
T
s
T
p
=
nT
f
T
c
log p+
nT
f
p
. (9)
Substituting the optimal number of processors p
∗
2
we
obtain
S
p
∗
2
=
nT
f
T
c
log p
∗
2
+
nT
f
p
∗
2
=
nT
f
q
T
c
log
nT
f
T
c
+
nT
f
nT
f
T
c
=
SINGLE-WALK PARALLELIZATION OF THE GENETIC ALGORITHM
589
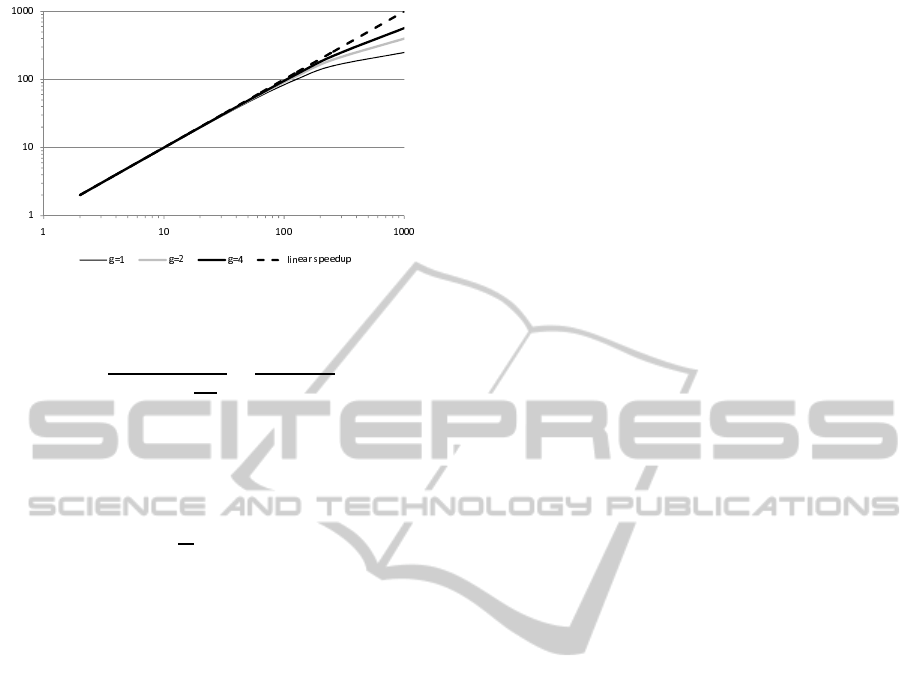
Figure 4: Theoretical speedups for the tree-based broad-
casting in the master-slave parallel genetic algorithm.
=
nT
f
T
c
(1+ log
nT
f
T
c
)
=
p
∗
2
1+ logp
∗
2
. (10)
This equation provides us with a maximal possible
speedup for the tree-base model of broadcasting for
the single-walk master-slave parallel genetic algo-
rithm.
The Figure 4 shows possible theoretical speedups
for a given ratio g =
T
f
T
c
, g = 1, 2, 4. As for sequen-
tial communication plotted on the Figure 2, linearity
of the speedup increases with the increase of the g
parameter. The parallel algorithm achieves the near-
linear speedup for the number of processors from the
range [1, p
∗
2
]. For the number of processors greater
than p
∗
2
speedup keeps on increasing.
6 REMARKS AND
CONCLUSIONS
In this paper we discussed some theoretical proper-
ties of a metaheuristics which can be used to solve
scheduling optimization problems. The tree-based
broadcasting model seems to be more efficient than
the sequential broadcasting model from the theoret-
ical point of view. In practice, it is possible to make
an additional improvement of the algorithm efficiency
by fulfilling of some processors idle time during the
communication phase – if the process is executed in
the cycle, one generation of the parallel genetic algo-
rithm after another, we can remove the synchronicity
constraint. In such a case the master processor can
execute a communication phase during a communica-
tion phase of the previous generation.
The proposed speedup estimation considered the
parallel genetic algorithm based on the master-slave
model of parallelism. The analyzed approaches give
us a theoretical approximation of the optimal number
of processors necessary to obtain the highest speedup.
Additionally, it is possible to determine theoretical
upper bounds for obtained speedups for the master-
slave model of the parallel genetic algorithm with a
single population kept by the master processor.
ACKNOWLEDGEMENTS
The work was partially supported by the Polish
Ministry of Science and Higher Education, grants
N N514 470439 (W. Bo˙zejko) and N N514 232237
(M. Wodecki).
REFERENCES
Bo˙zejko, W., Pempera, J., and Smutnicki, C. (2008a).
Multi-thread parallel metaheuristics for the flow shop
problem. In Artificial Intelligence and Soft Computing
(eds. L. Rutkowski, R. Tadeusiewicz, L.A. Zadeh, J.M.
Zurada), pages 454–462. IEEE Computational Intelli-
gence Society - Poland Chapter and the Polish Neural
Network Society.
Bo˙zejko, W., Pempera, J., and Smutnicki, C. (2008b). Paral-
lel single-thread strategies in scheduling. In Artificial
Intelligence and Soft Computing, volume 5097 of Lec-
ture Notes in Artificial Intelligence, pages 995–1006.
Springer.
Bo˙zejko, W., Uchro´nski, M., and aw Wodecki, M. (2010).
Parallel hybrid metaheuristics for the flexible job
shop problem. Computers & Industrial Engineering,
59:323–333.
Bo˙zejko, W. and Wodecki, M. (2006). A new inter-island
genetic operator for optimization problems with block
properties. volume 4029 of Lecture Notes in Artificial
Intelligence, pages 324–333. Springer.
Cahon, S., Melab, N., and Talbi, E.-G. (2004). Paradiseo on
condor-mw for optimization on computational grids.
http://www.lifl.fr/ cahon/cmw/index.html.
Cant´u-Paz, E. (2005). Theory of parallel genetic algo-
rithms. In Alba, E., editor, Parallel Metaheuristics,
pages 425–444. Wiley.
Czech, Z. (2002). Three parallel algorithms for simulated
annealing. volume 2328 of Lecture Notes in Artificial
Intelligence, pages 210–217. Springer.
Davidor, Y. (1991). A naturally occuring niche and species
phenomenon: The model and first results. In Proceed-
ings of the Fourth Internatinal Conference of Genetic
Algorithms, pages 257–263.
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
590
