
TOWARDS ROUTING FOR AUTONOMOUS ROBOTS
Using Constraint Programming in an Anytime Path Planner
Roman Barták
Faculty of Mathematics and Physics, Charles University, Praha, Czech Republic
Michal Zerola
Faculty of Nuclear Sciences and Physical Engineering, Czech Technical University, Praha, Czech Republic
Stanislav Slušný
Institute of Computer Science, Academy of Sciences of the Czech Republic, Praha, Czech Republic
Keywords: Vehicle routing, Autonomous robots, Constraint programming, Optimisation.
Abstract: Path planning is one of the critical tasks for autonomous robots. In this paper we study the problem of
finding the shortest path for a robot collecting waste spread over the area such that the robot has a limited
capacity and hence during the route it must periodically visit depots/collectors to empty the collected waste.
This is a variant of often overlooked vehicle routing problem with satellite facilities. We present two
approaches for this optimisation problem both based on Constraint Programming techniques. The former
one is inspired by the operations research model, namely by the network flows, while the second one is
driven by the concept of finite state automaton. The experimental comparison and enhancements of both
models are discussed with emphasis on the further adaptation to the real world environment.
1 INTRODUCTION
Recent advances in robotics have allowed robots to
operate in cluttered and complex spaces. However,
to efficiently handle the full complexity of the real-
world tasks, new deliberative planning strategies are
required. In this paper, we deal with the robot
performing a routine task of collecting waste for
example in large department stores where the remote
control is boring for humans and hence error prone.
In particular, we solve the problem of planning a
route for a single robot such that all waste is
collected, robot’s capacity is never exceeded, and
the route is as short as possible. We assume the
environment to be known and not changing, in
particular, the location of waste and depots is known
and the robot knows how to move between these
locations. To handle changes in the environment we
focus on anytime planning algorithms that can be re-
run when the initial task changes, for example, the
distances between the navigation points change due
to cluttered areas. We propose to use Constraint
Programming (CP) to solve the problem because of
the flexibility of CP. This allows us to use a base
model describing the core task and to add new
constraints later when necessary. Such a new
constraint could be the restriction on allowed
combinations of entrance and exit routes when
collecting the waste or visiting the depot for robots
with limited manoeuvring capabilities. Figure 1
gives an example of the initial environment (left)
and the found path for the robot (right).
Figure 1: Example of 6+3 robot planning task. The robot
(the big circle) collects waste (six small circles) and uses
collectors (three squares) to empty the bin when it is full.
313
Barták R., Zerola M. and Slušný S..
TOWARDS ROUTING FOR AUTONOMOUS ROBOTS - Using Constraint Programming in an Anytime Path Planner.
DOI: 10.5220/0003178703130320
In Proceedings of the 3rd International Conference on Agents and Artificial Intelligence (ICAART-2011), pages 313-320
ISBN: 978-989-8425-40-9
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

The task we are dealing with is to develop a
robot solving a specific routing problem – an often
overlooked variant of the standard Vehicle Routing
Problem (VRP). In our setting, the robot has to clean
out a collection of waste spread in a building, but
under the condition of not exceeding its internal
storage capacity at any time. The storage tank can be
emptied in one of available collectors. The goal is to
come up with the routing plan minimising the
travelled trajectory. This is a similar setting to a
Vehicle Routing Problem with Satellite Facilities
(VRPSF) studied in (Bard et al., 1998), where the
task is to deliver goods rather than to collect waste.
Our primary goal is to develop an algorithm that
returns good solutions in a short time (almost
anytime algorithm) and that can be easily extended
by additional constraints. Hence ad-hoc exact
techniques are not appropriate due to long runtime
and limited extendibility and we decided to use
Constraint Programming (CP) to solve the problem.
Neither of existing CP-oriented works solves the
above problem, but we can use them as the initial
motivation for the design of our constraint model.
Most of the routing models are based on the
formulation of the problem using network flows
(Simonis, 2006) so we also proposed a constraint
model based on this standard technique.
Nevertheless, the performance of this model was not
satisfactory in our experiments so we proposed a
radically new approach to model the problem using
a finite state automaton. In our preliminary
experiments, this model outperforms the traditional
model and can solve larger instances of the problem.
The paper is organised as follows. We will first
formally describe the problem to be solved. Then we
will formulate the traditional model based on
network flows that we customised to solve our
problem. After that we will describe the novel model
based on finite state automata. The paper will be
concluded by the preliminary experimental results.
2 PROBLEM FORMULATION
Recall that we are solving a single robot path
planning problem with the capacity constraint. The
robot’s environment consists of the navigation
points defined by the locations of waste and
collectors. We use a mixed weighted graph (V, E)
with both directed and undirected edges to represent
this environment. The reason for using undirected
edges is minimising the size of the representation.
The set of vertices V = {I} W C {D} consists
of the initial position I, the set W of waste vertices,
the set C of collectors and the destination vertex D.
From the initial position the robot has to visit some
waste so we have directed arcs from I to all vertices
in W. The robot can travel between the waste
vertices so we assume a complete undirected graph
between vertices in W. From any waste vertex the
robot can go to a collector so we use a directed edge
there and from any collector we can go to any waste
which is again modelled using a directed edge. We
need directed edges here as we need to count the
number of incoming and ongoing edges for the
collectors. There are no edges between the collector
vertices. As mentioned, we use a dummy destination
vertex that is connected to all collector vertices by a
directed edge. The weight of each edge describes the
distance between the navigation points. The edges
going to the dummy destination vertex D has zero
weight so the robot can actually finish at any
collector. The task to find a minimal-cost path
starting at I, finishing at D and visiting each vertex
in W exactly once such that the number of any
consecutive vertices from W does not exceed the
given capacity of the robot. Figure 2 shows the
schema of the graph with the navigation points.
Figure 2: A schema of the graph describing the robot’s
environment with the navigation points.
3 CP MODEL BASED ON
NETWORK FLOWS
The first model that we propose resembles the
traditional operations research models of vehicle
routing problems based on network flows and
Kirchhoff’s laws. Basically, we are describing
whether or not the robot traverses a given edge. For
every edge e we introduce a binary decision variable
X
e
stating whether the edge is used in the path (value
1) or not (value 0).
Let IN(v) and OUT(v) denote the set of incoming
and outgoing directed edges for the vertex v. For
example, for v W the set IN(v) contains the arc
from the vertex I and the arcs from the vertices in C.
Let ICD(v) be a set of undirected edges incident to
vertex v. This set is empty for the collector vertices;
for waste vertices it contains undirected edges
connecting the vertex with other waste vertices. The
following constraints describe that the robot leaves
the initial position I, reaches the destination position
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
314

D, and enters each collector c the same number of
times as it leaves it:
eOUT(I)
X
e
= 1,
eIN(D)
X
e
= 1,
(1)
c C:
eOUT
(
c
)
X
e
=
eIN
(
c
)
X
e
(2)
Let us now describe the constraint that each waste
vertex w is visited exactly once. It means that
exactly two edges incident to a waste vertex w are
active (used in the solution path) and there can be at
most one active incoming and outgoing directed
edge connecting the waste with the collectors or
with the initial node.
w W:
eOUT
(
w
)
IN
(
w
)
ICD
(
w
)
X
e
= 2 ,
(3)
w W:
eOUT
(
w
)
X
e
1,
(4)
w W:
eIN
(
w
)
X
e
1,
(5)
The above constraints describe any path leading
from I to D, but they also allow isolated loops as
Figure 3 shows. This is a known issue of this type of
model that is usually resolved by additional sub-tour
elimination constraints forcing any two subsets of
vertices to be connected.
Figure 3: An ineligible loop (left) satisfying the routing
(Kirchhoff’s) constraints.
In our particular setting, we need to carefully
select these pairs of subsets of vertices because there
could be collector vertices that are not visited.
Hence, we consider any pair of disjoint subsets
S
1
, S
2
(W C), such that neither S
1
nor S
2
consists of collector vertices only. More precisely,
we assume the pairs of subsets S
1
, S
2
such that:
S
2
= (W C) \ S
1
, S
1
W , S
2
W
(6)
The sub-tour elimination constraint can then be
expressed using the following formula ensuring that
there is at least one active edge between S
1
and S
2
.
eE: e S
1
e S
2
X
e
1.
(7)
Clearly, there is an exponential number of such pairs
S
1
and S
2
, which makes it impractical to introduce
all such sub-tour elimination constraints. Some
authors (Pop, 2007) propose using single or multi-
commodity flow principles to reduce the number of
constraints by introducing auxiliary variables.
However, our combination of directed and
undirected edges makes it complicated to use this
approach so we rather applied another approach
based on lazy (on-demand) insertion of sub-tour
elimination constraints. Briefly speaking, we start
with the model without the sub-tour elimination
constraints and we find a solution. If the solution
forms a valid path then we are done. Otherwise we
identify the isolated loops, add the sub-tour
elimination constraints for them and start the solver
with the updated model. This process is repeated
until a valid path is found. Obviously, it is a
complete procedure because in the worst case, all
sub-tour elimination constraints are added.
It remains to define the constraints describing the
limited capacity of the robot. For this purpose we
introduce auxiliary non-decision capacity variables
C
v
for every waste vertex v W. These variables
indicate the amount of waste in the robot after
visiting the particular vertex. The non-decision
character of the variables means that they are not
instantiated by the search procedure, but they are
instantiated by the inference procedure only. In
particular, if their domain becomes empty during
inference then it indicates inconsistency. The
following constraints are used during the inference
(w W). First, if the waste vertex w is visited
directly after the collector then there is exactly one
waste in the robot:
eIN(w)
X
e
= 1 C
w
= 1
(8)
Second, if the waste vertices u and v are visited
directly before respectively after w (or vice versa)
then the following constraints must hold between the
capacity variables:
e,f
ICD(w), e = {u,w}, f = {w,v}:
X
e
+ X
f
= 2 | C
u
– C
v
| = 2
(9)
e = {u,w}
ICD(w):
|
C
u
–
C
w
|
= 1
(10)
Finally, to restrict the capacity of the robot by
constant cap we use the following constraints for the
capacity variables:
w W: 1 C
w
cap.
(11)
The objective function to be minimised is the total
cost of edges used in the solution path:
Obj =
eE
X
e
. weight(e),
(12)
where weight(e) is the weight of edge e.
TOWARDS ROUTING FOR AUTONOMOUS ROBOTS - Using Constraint Programming in an Anytime Path Planner
315

3.1 Search Procedure
The constraint model describes how the inference is
performed so the model needs to be accompanied by
the search procedure that explores the possible
instantiations of variables X
e
.
Our search strategy resembles the greedy
approach for solving Travelling Salesman Problems
(TSP) (Ausiello et al., 1999). The variable X
e
for
instantiation is selected in the following way. If the
path is empty, we start at the initial position I and
instantiate the variable X
{I,w}
such that weight({I,w})
is the smallest among the weights of arcs going from
I. By instantiating the variable we mean setting it to
1; the alternative branch is setting the variable to 0.
If the path is non-empty then we try to extend it to
the nearest waste. Formally, if u is the last node in
the path then we select the variable X
{u,w}
with the
smallest weight({u,w}), where w is a waste vertex. If
this is not possible (due to the capacity constraint),
we go to the closest collector.
The optimisation is realised by the branch-and-
bound approach: after finding a solution with the
total cost Bound, the constraint Obj < Bound is
posted and search continues until any solution is
found. The last found solution is the optimum.
4 CP MODEL BASED ON
FINITE STATE AUTOMATA
The second model that we propose brings a radically
new approach not seen so far when modelling VRPs
or TSPs. Recall that we are looking for a path in the
graph that satisfies some additional constraints. We
can see this path as the word in a certain regular
language. Hence, we can base the model on the
existing regular constraint (Pesant, 2004). This
constraint allows a more global view of the problem
so the hope is that it can infer more information than
the previous model and hence decreases the search
space to be explored.
First, it is important to realise that the exact path
length is unknown in advance. Each waste vertex is
visited exactly once, but the collector vertices can be
visited more times and it is not clear in advance how
many times. Nevertheless, it is possible to compute
the upper bound on the path’s length. Let us assume
that the path length is measured as the number of
visited vertices, the robot starts at the initial position
and finishes at some collector vertex (we will use the
dummy destination in a slightly different meaning
here), and the weight/cost of arcs is non-negative.
Let K = |W| be the number of waste vertices and
cap 1 be the robot’s capacity. Then the maximal
path length is 2K+1. This corresponds to visiting a
collector vertex immediately after visiting a waste
vertex. Recall that each waste vertex must be visited
exactly once and there is no arc between the
collector vertices.
Our model is based on four types of constraints.
First, there is a restriction on the existence of a
connection between two vertices – a routing
constraint. This constraint describes the routing
network (see Figure 2). It roughly corresponds to the
constraints (1)-(5) from the previous model. Note
that the sub-tour elimination constraints (6)-(7) are
not necessary here. Second, there is a restriction on
the robot’s capacity stating that there in no
continuous subsequence of waste vertices whose
length exceeds the given capacity – a capacity
constraint. This constraint corresponds to the
constraints (8)-(11) from the previous model. Third,
each waste must be visited exactly once, while the
collectors can be visited more times (even zero
times) – an occurrence constraint. This restriction
was included in the constraints (1)-(5) of the
previous model, while we model it as a separate
constraint. Finally, each arc is annotated by a weight
and there is a constraint that the sum of the weights
of used arcs does not exceed some limit – a cost
constraint. This constraint is used to define the total
cost of the solution as in (12).
In the constraint model we use three types of
variables. Let N = 2K + 1 be the maximal path
length. Then we have N variables Node
i
, N variables
Cap
i
, and N variables Cost
i
(i = 1,...,N) so we
assume the path of maximal length. Clearly, the real
path may be shorter so we introduce a dummy
destination vertex that fills the rest of the path till the
length N. In other words, when we reach the dummy
vertex, it is not possible to leave it. This way, we can
always look for the path of length N and the model
gives flexibility to explore the shorter paths too.
The semantic of the variables is as follows. The
variables Node
i
describe the path hence their domain
is the set of numerical identifications of the vertices.
We use positive integers 1,...,K (K = |W|) to identify
the waste vertices, K+1,...,K+L for the collector
vertices (L = |C|), and 0 for the dummy destination
vertex. In summary, the initial domain of each
variable Node
i
consists of values 0,..., K+L. Cap
i
is
the used capacity of the robot after leaving vertex
Node
i
(Cap
1
= 0 as the robot starts empty), the initial
domain is {0,…, cap}. Cost
i
is the cost of the arc
used to leave the vertex Node
i
(Cost
N
= 0), the initial
domain consists of non-negative numbers. Formally:
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
316

i = 1,…,N (N = 2K + 1):
0 Node
i
K+L
0 Cap
i
cap, Cap
1
= 0
0 Cost
i
, Cost
N
= 0
(13)
We will start the description of the constraints with
the occurrence constraint saying that each waste
vertex is visited exactly once. This can be modelled
using the global cardinality constraint (Régin, 1996)
over the set {Node
1
,…, Node
N
}. The constraint is set
such that the each value from the set {1,.., K} is
assigned to exactly one variable from {Node
1
,…,
Node
N
} – each waste node is visited exactly ones.
The values {0, K+1,…, K+L} can be used any
number of times. Formally:
gcc({Node
1
,…, Node
N
},
{v:[1,1] v = 1,…,K,
0:[0,],
v:[0,] v = K+1,…,K+L}
(14)
where v:[min,max] means that value v is assigned to
at least min and at most max variables from
{Node
1
,…, Node
N
}.
The gcc constraint allows specifying the number
of appearances of the value using another variable
rather than using a fixed interval as in (14). Let D be
the variable describing the number of appearances of
value 0 (identification of the dummy vertex) in the
set {Node
1
,…, Node
N
}, then we can use the
following constraints instead of (14):
gcc({Node
1
,…, Node
N
},
{v:[1,1] v=1,…,K,
0:D,
v:[0,] v=K+1,…,K+L})
Node
N-D
> 0
(15)
(16)
The constraint (16) says that Node
N-D
is not a
dummy vertex; actually it is the last real vertex in
the path. We can also set the upper bound for D by
using the information about the minimal path length
(MinPathLength is a constant computed in advance):
D N – MinPathLength
(17)
These additional constraints (16) and (17) are not
necessary for the problem specification but they
improve inference (we use them in experiments).
The cost constraint can be easily described as
Obj =
i=1,…,N
Cost
i
(18)
so we can use the constraints Obj < Bound in the
branch-and-bound procedure exactly the same way
as in the previous model.
For the cost constraint to work properly we need
to set the value of Cost
i
variables. Recall that Cost
i
is
the cost/weight of the arc going from vertex Node
i
to
vertex Node
i+1
. Hence, we can connect the Cost
variables with the Node variables when specifying
the routing constraint. In particular, we use the
ternary constraints over the variables Node
i
, Cost
i
,
Node
i+1
i=1,…N-1. This set of constraints
corresponds to the idea of slide constraint (Bessiere
et al., 2007). We implement the constraint between
the variables Node
i
, Cost
i
, Node
i+1
as a ternary
tabular (extensionally defined) constraint; let us call
it link, where the triple (p, q, r) satisfies the
constraint if there is an arc from the vertex p to the
vertex r with the cost q. In other words, this table
describes the original routing network with the costs
extended by the dummy vertex. Formally:
link(p,q,r) eE: e = (p,r), q = weight(e)
(19)
(q = r = 0
(p = 0 p > K)
i = 1,…,2K: link(Node
i
, Cost
i
, Node
i+1
)
(20)
It remains to show how the capacity constraint is
realised. Briefly speaking, we use a similar approach
as for the routing constraint. The capacity constraint
is realised using a set of ternary constraints over the
variables Cap
i
, Node
i+1
, Cap
i+1
i=1,…N-1, again
exploiting the idea of slide constraint. The constraint
is implemented using a tabular constraint, let us call
it capa, with the following semantics. Triple (p, q, r)
satisfies this constraint if and only if
q is an identification of a collector vertex (q > K)
or a dummy vertex (q = 0) and r = 0
q is an identification of a waste node (0 < q K)
and r = p+1.
Recall that the domain of capacity variables is
{0,…,cap} so we never exceed the capacity of the
robot. Formally:
capa(p,q,r) q = r = 0
(21)
(q > K
r = 0)
(0 < q
K
r = p+1)
i = 1,…,2K: capa(Cap
i
, Node
i+1
, Cap
i+1
)
(22)
Any solution to the above described constraint
satisfaction problem defines a valid solution of our
single robot path planning problem with the capacity
constraint. Vice versa, any solution to the path
planning problem is also a feasible solution of the
specified constraint satisfaction problem. We omit
the formal proof due to limited space.
4.1 Search Procedure
Similarly to the previous model, it is important to
specify the search strategy. In this second model,
TOWARDS ROUTING FOR AUTONOMOUS ROBOTS - Using Constraint Programming in an Anytime Path Planner
317
only the variables Node
i
are the decision variables –
they define the search space. It is easy to realise that
the inference through the routing constraints (20)
decides the values of the Cost
i
variables and the
inference through the capacity constraints (22)
decides the values of the Cap
i
variables provided
that the values of all variables Node
i
are known.
When searching for the solution we first use a
greedy approach to find the initial solution (the
initial cost). This greedy algorithm instantiates the
variables Node
i
in the order of increasing i in such a
way that the arc with the smallest cost is preferred.
We select the node to which the least expensive arc
from the previously decided node leads. Naturally,
the capacity constraint is taken into account so only
the nodes such that the capacity is not exceeded are
assumed. This search procedure corresponds to the
search strategy of the previous model. The
difference in models allows us to use a fixed
variable ordering in the model based on finite
automata which simplifies implementation of the
search procedure. This second model also has fewer
decision variables but a larger branching factor.
To find the optimal solution we use a standard
branch-and-bound approach with restarts. To
instantiate the Node variables we use the min-dom
heuristic for the variable selection, that is, the
variable with the smallest current domain is
instantiated first. We select the values in the order
defined in the problem (the waste nodes are tried
before the collector nodes). Exactly like in the first
model after finding a solution with the total cost
Bound, the constraint Obj < Bound is posted and
search continues until any solution is found. The last
found solution is the optimum. Note that using the
well known and widely applied min-dom heuristic
for the variable selection is meaningful in this model
because we have larger domains, while the same
heuristic is useless for the previous model which
uses binary domains.
5 EXPERIMENTAL RESULTS
In this section we will present the preliminary
experimental evaluation of the presented solving
techniques. As there is no standard benchmark set
for the studied problem, we generated own problem
instances. We used a square-sized robot arena where
the positions of the waste and the initial location of
the robot were uniformly distributed. The collectors
were uniformly distributed along the boundaries of
the arena and the weights set up as a point-to-point
distance using the Euclidean metric. All the
following measurements were performed on Intel
Xeon CPU@2.5GHz with 4 GB of RAM, running a
Debian GNU Linux operating system.
5.1 Performance of the
Network Flow Model
As stated earlier, the model based on network flows
corresponds to the traditional operations research
approach, but we modified the model to describe
specifics of our robot routing problem. The model
was implemented in Java using Choco
(http://choco.emn.fr), an open-source constraint
programming library. The optimisation search
strategy uses the built-in branch-and-bound method,
while all constraints correspond to the mathematic
formulations described earlier.
Figure 4 shows the runtime (a logarithmic scale)
to obtain the optimal solution as a function of the
instance size measured by the number of waste and
by the number of collectors. We generated 15
instances for each problem size and the graph shows
the average time the solver needs for finding and
proving the optimality of the solution. The capacity
of robot was 3.
Figure 4: Runtime (seconds) for the network flow model.
As already mentioned in (Bard et al., 1998), the
satellite facilities in VRP (or collectors in robotics
case) heavily increase the complexity of the
problem. The initial experiment shows that the
runtime increases exponentially with the number of
waste but the runtime is not significantly affected by
the increased number of collectors. In fact it seems
that for different quantities of waste there are
different numbers of collectors where the best
runtime is achieved. This is an interesting
observation claiming that for a given number of
waste there is some number of collectors that gives
3
4
5
6
7
8
15
1E‐06
1E‐05
0,0001
0,001
0,01
0,1
1
10
100
3
4
5
6
7
8
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
318

the best result. Nevertheless, this observation
requires additional experiments to confirm it.
5.2 Performance of the Finite State
Automaton Model
The network flow model represents a standard
approach to solving the Vehicle Routing Problems
so we compared our novel constraint model based
on the finite state automaton directly to this
approach. The second model was implemented in
SICStus Prolog (http://www.sics.se/sicstus). Figure
5 shows the runtime (a logarithmic scale) to obtain
the optimal solution using the constraint model
based on finite state automata using the same
problems as for the model based on network flows
(Figure 4). The result also shows the exponential
grow with the increased number of waste and
weaker dependence on the number of collectors.
Figure 5: Runtime (seconds) for the FSA model.
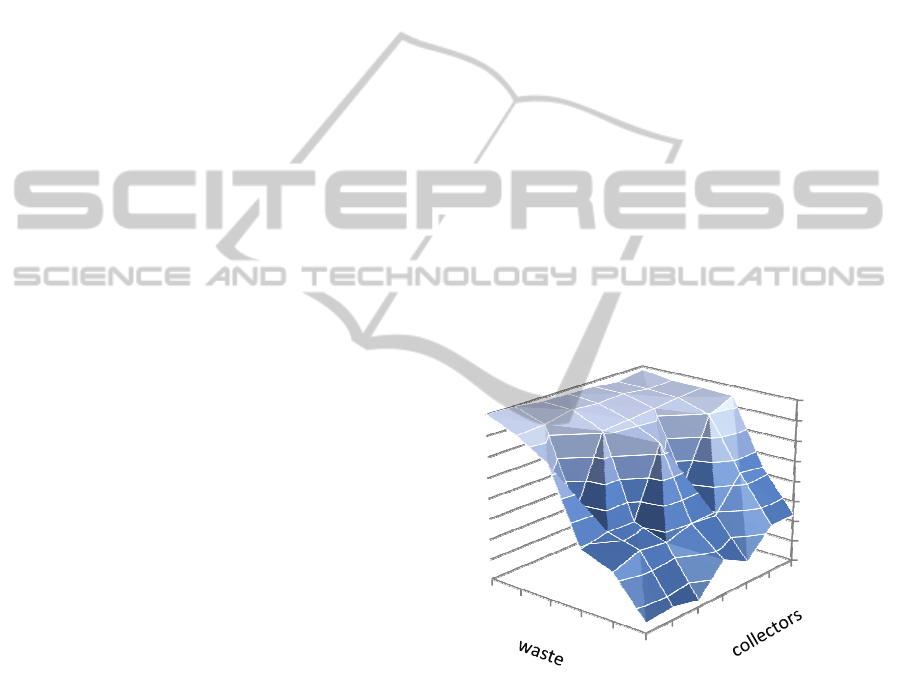
Figure 6: Time difference (seconds) between the CP
models. Positive values means that the model based on
finite state automata is faster.
To directly compare both models, we generated a
difference graph showing the difference of runtimes
for the network model and for the automata model –
the values above zero mean faster automata model,
while the times below zero mean faster network
model. Figure 6 shows these difference times. The
conclusion drawn from this graph is as follows. The
automata-based model is visibly better for a smaller
number of collectors where the problem is more
constrained and the capacity constraints can prune
more of the search space. A bit surprisingly, it seems
that the network-based model is better when the
number of collectors becomes larger. This feature
will require a further investigation.
6 CONCLUSIONS
We proposed two constraints models for deliberative
planning of the robot picking up all waste in a
known environment and putting them to collectors
while assuming a limited capacity of the robot. We
used a constraint model based on network flows that
is traditionally applied to this type of routing
problems and we developed a completely new model
based on finite state automata. Using the constraint
programming techniques allowed us to naturally
define the underlying model for which the solver
was able to find the first solution in hundreds of
microseconds on problems of reasonable size. The
preliminary experiments showed some interesting
behaviour of the model in relation to the number of
collectors that we shall further investigate.
ACKNOWLEDGEMENTS
The research is supported by the Czech Science
Foundation under the contract P202/10/1188, by
the grants LC07048 and LA09013 of the Ministry of
Education of the Czech Republic, and by the project
KJB100300804 of GA AV ČR.
REFERENCES
Ausiello, G., Crescenzi, P., Kann, V., Marchetti-
Spaccamela, A., Protasi, M., 1999. Complexity and
Approximation: Combinatorial Optimization Problems
and Their Approximability Properties, Springer.
Bard, J. F., Huang, L., Dror, M., Jaillet, P., 1998. A branch
and cut algorithm for the VRP with satellite facilities.
IIE Transactions 30(9), Springer, pp. 821-834.
Bessiere, C., Hebrard, E., Hnich, B., Kiziltan, Z.,
Quimper, C. G., Walsh, T., 2007. Reformulating
global constraints: The Slide and Regular Constraints.
3
4
5
6
7
8
15
1E‐06
1E‐05
0,0001
0,001
0,01
0,1
1
10
100
3
4
5
6
7
8
3
4
5
6
7
8
15
‐200
‐150
‐100
‐50
0
50
100
150
3
4
5
6
7
8
TOWARDS ROUTING FOR AUTONOMOUS ROBOTS - Using Constraint Programming in an Anytime Path Planner
319

In Proceedings of SARA, LNCS 4612, Springer, pp.
80-92.
Pesant, G., 2004. A Regular Language Membership
Constraint for Finite Sequences of Variables. In
Principles and Practice of Constraint Programming,
LNCS 3285, Springer, pp. 482-495.
Pop, P. C., 2007. New Integer Programming Formulations
of the Generalized Travelling Salesman Problems.
American Journal of Applied Sciences 11, pp. 932-
937.
Régin, J. C., 1996. Generalized Arc Consistency for
Global Cardinality Constraint. In Proceedings of
AAAI, AAAI Press, pp. 209-215.
Simonis, H., 2006. Constraint applications in networks. In
Handbook of Constraint Programming, Elsevier, pp.
875-903.
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
320
