EFFICIENT SYMBOLIC SUPERVISORY SYNTHESIS AND GUARD

GENERATION

Evaluating Partitioning Techniques for the State-space Exploration

Z. Fei, S. Miremadi

Department of Signals and Systems, Chalmers University of Technology, Gothenburg, Sweden

Akesson, B. Lennartson

Department of Signals and Systems, Chalmers University of Technology, Gothenburg, Sweden

Keywords:

Supervisory control theory, Deterministic ﬁnite automata, Symbolic representation, Reachability search,

Propositional formula.

Abstract:

The supervisory control theory (SCT) is a model-based framework, which automatically synthesizes a super-

visor that restricts a plant to be controlled based on speciﬁcations to be fulﬁlled. Two main problems, typically

encountered in industrial applications, prevent SCT from having a major breakthrough. First, the supervisor

which is synthesized automatically from the given plant and speciﬁcation models might be incomprehensible

to the users. To tackle this problem, an approach was recently presented to extract compact propositional

formulae (guards) from the supervisor, represented symbolically by binary decision diagrams (BDD). These

guards are then attached to the original models, which results in a modular and comprehensible representation

of the supervisor. However, this approach, which computes the supervisor symbolically in the conjunctive way,

might lead to another problem: the state-space explosion, because of the large number of intermediate BDD

nodes during computation. To alleviate this problem, we introduce in this paper an alternative approach that is

based on the disjunctive partitioning technique, including a set of selection heuristics. Then this approach is

adapted to the guard generation procedure. Finally, the efﬁciency of the presented approach is demonstrated

on a set of benchmark examples.

1 INTRODUCTION

The analysis of reactive systems has been paid much

attention by researchers and scientists in the computer

science community. One of the classic methods to an-

alyze reactive systems is utilizing formal veriﬁcation

techniques, such as model checking, to verify whether

the system always fulﬁll speciﬁcations. Nevertheless,

from the control engineering point of view, instead of

verifying the correctness of the system, a controller

which guarantees that the system behaves according

to speciﬁcations is preferred. The Supervisory Con-

trol Theory (SCT) (Ramadge and Wonham, 1987; Ra-

madge and Wonham, 1989; Cassandras and Lafor-

tune, 2008) provides such a control-theoretic frame-

work to design a device, called the supervisor, for

reactive systems referred as discrete event systems

(DESs). Given a model of the system to be controlled,

the plant, and the intended behavior, the speciﬁca-

tion, the supervisor can be automatically synthesized,

guaranteeing that the closed-loop system fulﬁlls given

speciﬁcations. SCT has been applied for various ap-

plications in different areas such as automated manu-

facturing lines and embedded systems (Balemi et al.,

1993; Feng et al., 2007; Shoaei et al., 2010).

Generally, a supervisor is a function that, given

a set of events, restricts the plant to execute desired

events according to the speciﬁcation. A typical issue

is how to realize such a control function efﬁciently

and represent it appropriately. Since the synthesis

task involves a series of reachability computations,

as the DES becoming more complicated, the tradi-

tional explicit state-space traversal algorithm may be

intractable due to the space-state explosion problem.

By using binary decision diagrams (BDDs) (Akers,

1978; Bryant, 1992), the supervisor can be repre-

sented and computed symbolically such that the state-

space explosion problem is alleviated to some extent.

However, the symbolic computation is not a silver

bullet. Transforming from the traditional explicit stat-

106

Fei Z., Miremadi S., Åkesson K. and Lennartson B..

EFFICIENT SYMBOLIC SUPERVISORY SYNTHESIS AND GUARD GENERATION - Evaluating Partitioning Techniques for the State-space Exploration.

DOI: 10.5220/0003178801060115

In Proceedings of the 3rd International Conference on Agents and Artiﬁcial Intelligence (ICAART-2011), pages 106-115

ISBN: 978-989-8425-40-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

space traversal algorithm into a BDD-based compu-

tation scheme does not guarantee that the algorithm

will become remarkably efﬁcient. Thus numerous re-

search has been performed to improve the efﬁciency

of symbolic computations. In this paper, we mainly

focus on partitioning techniques, which decompose

the state-space into a set of structural components and

utilize these partitioned components to realize efﬁ-

cient reachability computations.

Everything has its pros and cons. With BDD-

based traversal algorithms, some larger DESs could

be solved without causing the state-space explosion.

Meanwhile, another problem is arising from the BDD

representation of the resultant supervisor. Since the

original models have been reformulated and encoded,

it is cumbersome for the users to relate each state with

the corresponding BDD variables. Therefore, it is

more convenient and natural to represent the super-

visor in a form similar to the models. In (Miremadi,

2010), a promising approach is presented, where a set

of minimal and tractable logic expressions, referred

to as guards, are extracted from the supervisor and at-

tached to the original models of the closed-loop sys-

tem. However, this approach computes the supervi-

sor symbolically based on the conjunctive partition-

ing technique. This might lead to the state-space ex-

plosion, because of the large number of intermediate

BDD nodes during computation.

The main contribution of this paper is adapting a

symbolic supervisory synthesis approach to the guard

generation procedure, to make it applicable for indus-

trially interesting applications. The approach auto-

matically synthesizes a supervisor by taking the ad-

vantage of the disjunctive partitioning technique. The

monolithic state-space is then splitted into a set of

simpler components and the reachability search is

performed structurally with a set of heuristic deci-

sions. Moreover, the guard generation procedure is

tailored to use the partitioned structure to extract the

simpliﬁed guards and attach them to the original mod-

els. Finally, a comparison of algorithm efﬁciency be-

tween two partitioning techniques is made by apply-

ing them to a set of benchmark examples.

The paper is organized as follows: For the readers

who might be unfamiliar with the supervisory control

theory, Section 2 gives an informal and brief explana-

tion. Section 3 provides some preliminaries that are

used throughout the paper. The symbolic supervisory

synthesis and the guard generation procedure will be

discussed in detail in Section 4 and 5. In Section 6,

we apply what we have discussed and implemented

to several real case studies. Finally we end up with

the evaluation of two used partitioning techniques in

Section 6.2 and some conclusions in Section 7.

2 MOTIVATING EXAMPLE

For readers who might be unfamiliar with the super-

visory control theory (SCT), the following simple ex-

ample gives a brief overview and states what exact

problem this paper is about to solve.

Consider a resource booking problem where two

industrial robots need to book two resources in oppo-

site order to carry out their tasks. To avoid collisions,

a constraint requires that two robots are not allowed

to occupy two zones simultaneously.

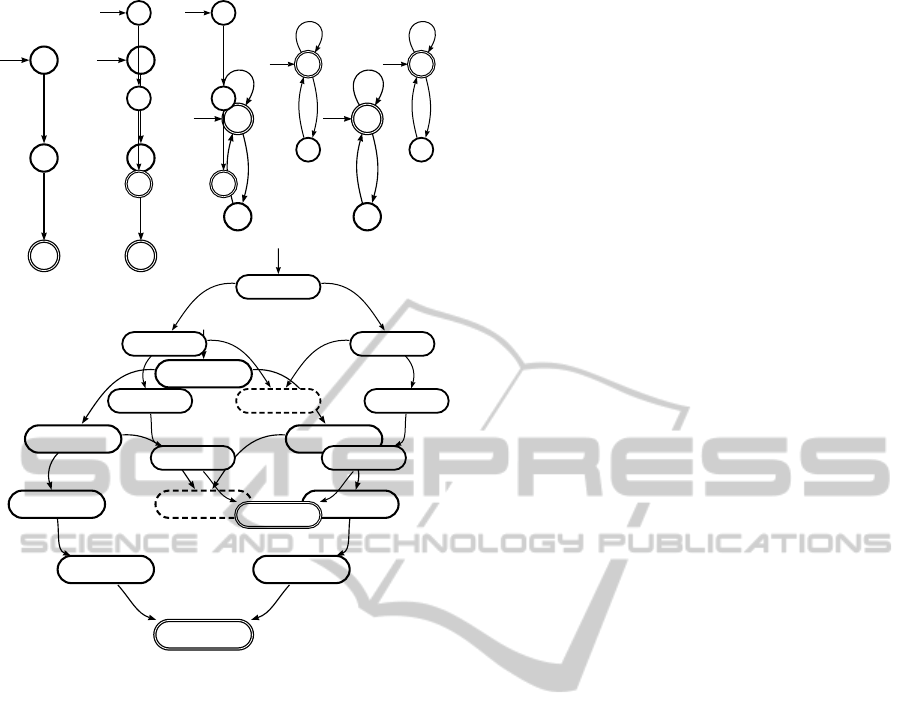
Fig. 1 shows one way to model the system as the

state machines, or automata. Fig.1a and 1b depict the

robot (plant) models and Fig. 1c and 1d depict the re-

source (speciﬁcation) models. The states having an

incoming arrow from outside denote the beginning

of the task, while the states having double circles,

called marked states, denote the accomplishment of

the task. The event use

means that Robot A uses

Resource 1. The other events can be interpreted sim-

ilarly. The goal of the SCT is to automatically syn-

thesize a minimally restrictive supervisor from these

modular models. Traditionally, to do this, the algo-

rithm starts with the composition (formally described

in Section 3.1) of all the automata as the initial candi-

date supervisor S0 (Fig. 1e), where unreachable states

have been excluded. Then the undesirable states will

be removed iteratively. Generally, undesirable states

can either be blocking or uncontrollable. A state is

blocking when no marked state can be reached, while

uncontrollable states are deﬁned in Section 3.1. In

Fig. 1e, we have one blocking state hq

which depicts the situation where Robot A has booked

Resource 1 and is trying to book Resource 2, while

Robot B has booked Resource 2 and is trying to book

Resource 1. In such case, none of the robots can do

other movements, which is a deadlock situation. Af-

ter removing the blocking state together with the as-

sociated transitions, a nonblocking supervisor is pro-

duced.

It can be observed that for such a simple example,

the composed automaton contains 12 states (unreach-

able states from the initial state have been removed).

With the system getting more complicated, the com-

posed automaton will become signiﬁcantly larger. To

alleviate this problem, a well known strategy is to rep-

resent the state space symbolically by using Binary

Decision Diagrams (BDDs). In (Miremadi, 2010),

based on this principle, an alternative approach is pre-

sented, where guards are generated to prevent the con-

trolled system to reach undesirable states. The advan-

tage of this approach is that it never constructs the

composed automaton, which means that an incom-

prehensible BDD representation of the supervisor is

EFFICIENT SYMBOLIC SUPERVISORY SYNTHESIS AND GUARD GENERATION - Evaluating Partitioning

Techniques for the State-space Exploration

107

use

(a) A.

use

(b) B.

use

(d) D.

, q

i hq

, q

i hq

, q

ihq

, q

i hq

, q

use

(e) S

Figure 1: Example. 1a-1b) Robot automata A and B,

1c-1d) resource automata C and D, and (1e) a super-

visor candidate S

avoided. Instead, the approach characterizes a super-

visor by a set of minimal guards that are attached to

the original models to represent the supervisor behav-

ior. Fig.2 shows the application of the guard genera-

tion to the example, where the variables v

, v

are introduced to hold the current states of the corre-

sponding automata.

The intention of this paper is to improve the guard

generation procedure by introducing an alternative

symbolic approach. This approach, which is based on

the disjunctive partitioning technique, partitions the

transition function into a set of simple but structural

components. These components, having the disjunc-

tive connection relation between each other, therefore

can be used to search the state-space without con-

structing a total transition function for the composed

automaton. Besides, to keep the intermediate number

of BDD nodes as small as possible, the approach in-

cludes a set of selection heuristics to search the state-

space in a structural way.

use

6= q

use

(a) A.

use

= q

use

(b) B.

use

6= q

use

= q

use

(d) D.

Figure 2: Guards representing the behavior of the su-

pervisor for the example.

3 PRELIMINARIES

This section provides some preliminaries which are

used throughout the rest of the paper.

3.1 Supervisory Control Theory

Generally, a DES can either be described by textual

expressions, such as regular expressions or graphi-

cally by for instance Petri nets or automata. For this

paper, we focus on deterministic ﬁnite automata.

A deterministic ﬁnite automaton is a ﬁve-tuple

(Q,Σ,δ, q

init

), where Q is a ﬁnite set of states,

init

∈ Q is the initial state, Q

⊆ Q is the set of

marked or accepting states, and the alphabet Σ is the

ﬁnite set of events. The transitions of the states are

expressed by the partial transition function δ, where

δ(q,σ) = ´q means that there exists a transition labeled

by event σ ∈ Σ from the source-state state q ∈ Q to the

target-state state ´q ∈ Q.

In SCT, the events in the alphabet, Σ can either be

controllable or uncontrollable. Therefore, Σ can be di-

vided into two disjoint subsets, the controllable event

set Σ

, and the uncontrollable event set, Σ

. The su-

pervisor is only allowed to restrict controllable events

from occurring in the plant.

The goal of SCT is to automatically synthesize a

maximally permissive supervisor, restricting the be-

havior of the plant to fulﬁll the given speciﬁcation.

Generally, the plant or the speciﬁcation could be mod-

ularly expressed by a number of sub-plants or sub-

speciﬁcations. The composition of two or more au-

tomata is realized by the full synchronous operator

k, deﬁned in (Hoare, 1985). For instance, if the

Figure 1: Example.1a-1b) Robot automata A and B, 1c-1d)

resource automata C and D, and 1e) a supervisor candidate

avoided. Instead, the approach characterizes a super-

visor by a set of minimal guards that are attached to

the original models to represent the supervisor behav-

ior. Fig.2 shows the application of the guard genera-

tion to the example, where the variables v

, v

are introduced to hold the current states of the corre-

sponding automata.

The intention of this paper is to improve the guard

generation procedure by introducing an alternative

symbolic approach. This approach, which is based on

the disjunctive partitioning technique, partitions the

transition function into a set of simple but structural

components. These components, having the disjunc-

tive connection relation between each other, therefore

can be used to search the state-space without con-

structing a total transition function for the composed

automaton. Besides, to keep the intermediate number

of BDD nodes as small as possible, the approach in-

cludes a set of selection heuristics to search the state-

space in a structural way.

use

(a) A.

use

(b) B.

use

(d) D.

, q

i hq

, q

i hq

, q

ihq

, q

i hq

, q

use

(e) S

Figure 1: Example. 1a-1b) Robot automata A and B,

1c-1d) resource automata C and D, and (1e) a super-

visor candidate S

avoided. Instead, the approach characterizes a super-

visor by a set of minimal guards that are attached to

the original models to represent the supervisor behav-

ior. Fig.2 shows the application of the guard genera-

tion to the example, where the variables v

, v

are introduced to hold the current states of the corre-

sponding automata.

The intention of this paper is to improve the guard

generation procedure by introducing an alternative

symbolic approach. This approach, which is based on

the disjunctive partitioning technique, partitions the

transition function into a set of simple but structural

components. These components, having the disjunc-

tive connection relation between each other, therefore

can be used to search the state-space without con-

structing a total transition function for the composed

automaton. Besides, to keep the intermediate number

of BDD nodes as small as possible, the approach in-

cludes a set of selection heuristics to search the state-

space in a structural way.

use

6= q

use

(a) A.

use

= q

use

(b) B.

use

6= q

use

= q

use

(d) D.

Figure 2: Guards representing the behavior of the su-

pervisor for the example.

3 PRELIMINARIES

This section provides some preliminaries which are

used throughout the rest of the paper.

3.1 Supervisory Control Theory

Generally, a DES can either be described by textual

expressions, such as regular expressions or graphi-

cally by for instance Petri nets or automata. For this

paper, we focus on deterministic ﬁnite automata.

A deterministic ﬁnite automaton is a ﬁve-tuple

(Q,Σ, δ,q

init

), where Q is a ﬁnite set of states,

init

∈ Q is the initial state, Q

⊆ Q is the set of

marked or accepting states, and the alphabet Σ is the

ﬁnite set of events. The transitions of the states are

expressed by the partial transition function δ, where

δ(q,σ) = ´q means that there exists a transition labeled

by event σ ∈ Σ from the source-state state q ∈ Q to the

target-state state ´q ∈ Q.

In SCT, the events in the alphabet, Σ can either be

controllable or uncontrollable. Therefore, Σ can be di-

vided into two disjoint subsets, the controllable event

set Σ

, and the uncontrollable event set, Σ

. The su-

pervisor is only allowed to restrict controllable events

from occurring in the plant.

The goal of SCT is to automatically synthesize a

maximally permissive supervisor, restricting the be-

havior of the plant to fulﬁll the given speciﬁcation.

Generally, the plant or the speciﬁcation could be mod-

ularly expressed by a number of sub-plants or sub-

speciﬁcations. The composition of two or more au-

tomata is realized by the full synchronous operator

k, deﬁned in (Hoare, 1985). For instance, if the

Figure 2: Guards representing the behavior of the supervi-

sor for the example.

3 PRELIMINARIES

This section provides some preliminaries which are

used throughout the rest of the paper.

3.1 Supervisory Control Theory

Generally, a DES can either be described by textual

expressions, such as regular expressions or graphi-

cally by for instance Petri nets or automata. For this

paper, we focus on deterministic ﬁnite automata.

A deterministic ﬁnite automaton is a ﬁve-tuple

(Q,Σ,δ, q

init

), where Q is a ﬁnite set of states,

init

∈ Q is the initial state, Q

⊆ Q is the set of

marked or accepting states, and the alphabet Σ is the

ﬁnite set of events. The transitions of the states are

expressed by the partial transition function δ, where

δ(q,σ) = ´q means that there exists a transition labeled

by event σ ∈ Σ from the source-state state q ∈ Q to the

target-state state ´q ∈ Q.

In SCT, the events in the alphabet, Σ can either be

controllable or uncontrollable. Therefore, Σ can be di-

vided into two disjoint subsets, the controllable event

set Σ

, and the uncontrollable event set, Σ

. The su-

pervisor is only allowed to restrict controllable events

from occurring in the plant.

The goal of SCT is to automatically synthesize

a maximally permissive supervisor, restricting the

behavior of the plant to fulﬁll the given speciﬁcation.

Generally, the plant or the speciﬁcation could be

modularly expressed by a number of sub-plants

or sub-speciﬁcations. The composition of two or

more automata is realized by the full synchronous

operator k, deﬁned in (Hoare, 1985). For instance,

if the plant is given as a number of sub-plants

,.. .,P

, the plant P is computed by synchronizing

the sub-plants P = P

k . .. k P

. More speciﬁcally, let

= (Q

,Σ

,δ

init

),i = 1,2 be two automata.

The full synchronous composition of A

and A

re-

sults in A

k A

= (Q

1k2

,Σ

∪Σ

,δ

1k2

init

×Q

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

108

where Q

1k2

⊆ Q

× Q

and q

1k2

init

= (q

init

). The

composite transition function δ

1k2

is deﬁned as

follows.

1k2

((q

),σ) =











,σ)× δ

,σ) if σ ∈ Σ

∩ Σ

,σ)× {q

} if σ ∈ Σ

\Σ

} × δ

,σ) if σ ∈ Σ

\Σ

undeﬁned otherwise

(1)

Additionally, given a plant P and a speciﬁcation Sp,

two properties (Ramadge and Wonham, 1987; Ra-

madge and Wonham, 1989; Cassandras and Lafor-

tune, 2008) that the supervisor has or should have are:

1. Controllability: The supervisor S is never allowed

to disable any uncontrollable event that might be

generated by the plant P. Let Σ

be the set of un-

controllable event set. A state q

is said to be an

uncontrollable state if it is enabled by the plant P,

while disabled by the supervisor S.

2. Non-blocking: This is a progress property en-

forced by the supervisor S, which guarantees that

at least one marked state is always reachable in

the closed-loop system, S k P.

3.2 Binary Decision Diagrams

Binary Decision Diagrams (BDDs), used for repre-

senting Boolean functions, can be extended to sym-

bolically represent states, events and transitions of au-

tomata. In contrast to explicit representations, which

might be computationally expensive in terms of time

and memory, BDDs often generate compact and op-

eration efﬁcient representations.

A binary decision diagram is a directed acyclic

graph (DAG) consisting of two kinds of nodes: de-

cision nodes and terminal nodes. Given a set of

Boolean variables V , a BDD is a Boolean func-

tion f : 2

→ {0, 1} which can be recursively ex-

pressed using Shannon’s decomposition (Shannon

and Weaver, 1949). Besides, a variable v

has a lower

(higher) order than variable v

if v

is closer (further)

to the root and is denoted by v

≺ v

. The variable or-

dering will impact the number of BDD nodes. How-

ever, ﬁnding an optimal variable ordering of a BDD is

an NP-complete problem (Bollig and Wegener, 1996).

In this paper, a simple but powerful heuristic based on

Aloul’s Force algorithm (Aloul et al., 2003) is used to

compute a suitable static variable ordering.

Symbolic Representation of Automata

The BDD data structure can be extended to also rep-

resent models such as automata. The key point is to

make use of characteristic functions.

Table 1: Set operations on the characteristic functions.

Sets/Operations Characteristic function

0 0

U 1

t ∈ S χ

↔ 1

⊆ S

(χ

→ χ

) ↔ 1

U\S ¬χ

∪ S

∨ χ

∩ S

∧ χ

Given a ﬁnite state set U as universe, for every S ⊆ U,

the characteristic function can be deﬁned as follows:

(α) =

1 α∈S

0 α/∈S

Set operations can be equivalently carried on cor-

responding characteristic functions. For example,

∪ S

, (S

⊆ U ) can be mapped equivalently to

∨ χ

, since S

∪ S

= {α ∈ U | α ∈ S

∨ α ∈ S

Table 1 shows more operations on characteristic func-

tions.

The elements of a ﬁnite set can be expressed as

a Boolean vector. So a set with n elements, re-

quires a Boolean vector of length dlog

ne. Just like

the case of coding the states in a set, binary encod-

ing of the transition function δ follows the same rule

but with the difference that the transition function

distinguishes between source-states and target states.

Hence, we need two Boolean vectors with different

sets of Boolean variables to express the domain of

source-states and target-states respectively.

4 BDD-BASED PARTITIONING

COMPUTATION

As mentioned above, one of the challenges to apply

SCT in industry is the state-space explosion problem

when synthesizing the supervisor. After adopting Bi-

nary Decision Diagrams, the problem can be allevi-

ated to some extent. But that’s not enough, since the

intuitive total representation of the transition function

might still be huge. Two partitioning techniques are

discussed in this section.

4.1 Safe-state Synthesis

The safe-state algorithm, an efﬁcient supervisor syn-

thesis algorithm, formally deﬁned in (Vahidi et al.,

2006), is used in this paper. The algorithm creates the

supervisor by ﬁrst building the candidate S0 = P k Sp,

then removing states from Q

until the remaining

safe states are both nonblocking and controllable.

EFFICIENT SYMBOLIC SUPERVISORY SYNTHESIS AND GUARD GENERATION - Evaluating Partitioning

Techniques for the State-space Exploration

109

As Algorithm 1 shows, given a set of forbidden

states Q

, the algorithm computes the set of safe states

by iteratively removing the blocking states (Re-

strictedBackward in line 5) and the uncontrollable

states (UncontrollableBackward in line 6). Note that

after the termination of the algorithm, not all of the

safe states are reachable from the initial state. There-

fore, a forward reachability search is needed to ex-

clude the safe states which are not reachable. The

safe-state algorithm is discussed in more detail in

(Vahidi et al., 2006).

Algorithm 1: The Safe State Synthesis.

1: input : Q

2: let X

:= Q

,k := 0

3: repeat

4: k := k + 1

5: Q

:= RestrictedBackward(Q

k−1

)

6: Q

:= UncontrollableBackward(Q

)

7: X

:= X

k−1

∪ (Q

)

8: until X

= X

k−1

9: return Q

4.2 Efﬁcient State Space Search

Not surprisingly, the backward and forward reacha-

bility searches turn out to be the bottle-neck of the

algorithm presented above. The problem with the in-

tuitive reachability is that for the large and compli-

cated modular DES, the BDD representation of the

total transition function δ

SpkP

is often too large to be

constructed. The natural way to tackle the complex-

ity of the transfer function is to split it into a set of

less complex partial functions with a connection be-

tween them. Such methods are based on conjunctive

and disjunctive partitioning techniques.

Conjunctive Representation

Conjunctive partitioning, introduced in (Burch et al.,

1991; Burch et al., 1994), is an approach to repre-

sent synchronous digital circuits where all transitions

happen simultaneously. In the context of DES, the

conjunctive partitioning of the full synchronous com-

position can be achieved by adding self-loops to the

automata for events that are not included in their orig-

inal alphabets. This leads to a situation where all au-

tomata have equal alphabet. Therefore, the conjunc-

tive transition function

for the automaton A

and the

total transition function can be deﬁned as follows:

,σ) =







,σ) if δ

,σ)

if σ /∈ Σ

undeﬁed otherwise

(2)

δ =

1≤i≤n

(3)

By making use of the above equations (2) and (3),

we can search the state-space without constructing

the total transition function. Algorithm 2 applies this

technique for the forward reachability search. Assum-

ing that the automaton set A = {A

,.. .,A

} and the

state q = hq

,.. .,q

i, the algorithm explores the

target state ´q by performing each conjunctive transi-

tion function

with arguments (the local state q

and

the event σ ∈ Σ) to get each local target state ´q

Algorithm 2: ConjForwardReachability.

1: input : Q

init

,.. .,

},Σ

2: let Q

:= Q

init

,k := 0

3: repeat

4: k := k + 1

5: Q

:= Q

k−1

∪ { ´q | ∃q ∈ Q

k−1

and ∃σ ∈ Σ,

∀i ∈ {1, 2,... ,n} such that

,σ) = ´q

}

6: until Q

= Q

k−1

7: return Q

Disjunctive Representation

The conjunctive partitioning of the transition rela-

tion works well for formal veriﬁcation of synchronous

digital circuits. However, because of the asyn-

chronous feature of the full synchronous composition

in SCT, the intermediate states (Q

k−1

) can still cause

the explosion problem when performing the reach-

ability search, which prevents the conjunctive parti-

tioning technique from being applied to large systems

in SCT. The disjunctive partitioning of the full syn-

chronous composition, explained subsequently, on the

other hand, is then shown to be an appropriate parti-

tioning.

Assuming the automaton set A = {A

,.. .,A

} and

the state q = hq

,.. .,q

i, a disjunctive transition

function, the partial transition function

, is deﬁned

based on the event σ ∈ Σ

and the dependent set D(A

(q,σ) =





∈D(A

)

i, j

,σ)





∧





/∈D(A

)

↔ q





(4)

i, j

,σ) =



,σ) if σ ∈ Σ

∩ Σ

otherwise

(5)

and

D(A

) = {A

∈ A | ∃A

∈ A where Σ

∩ Σ

0} (6)

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

110

The total transition function is deﬁned as

δ =

1≤i≤n

(7)

The construction of the dependent set for each au-

tomaton can be obtained through calculating which

automaton shares any event with it. Taking Fig. 1

as an example, for the automaton A, since it shares

the events use

, use

with the automaton C and the

event use

with the automaton D, D(A) can be con-

structed as follows:

D(A) = {A,C,D}

Besides, the total transition function deﬁned for the

state hq

i and the event use

can be ob-

tained by computing

and

, since use

only be-

longs to Σ

and Σ

. By using equations (4) and (5), it

can be inferred that

δ(hq

i,use

) =

(hq

i,use

)

(hq

i,use

) = hq

Notice that the disjunctive transition function repre-

sented in BDDs, is shown explicitly here to easily un-

derstand.

4.3 Workset based Strategies

In Section 4.2, we suggested the use of partitioning

techniques to deal with the large number of interme-

diate BDD nodes. However, using partitioning tech-

niques alone is not enough to yield efﬁcient BDD-

based reachability algorithms. In (Byr

od et al., 2006),

it has been shown that random structural reachabil-

ity search yields poor compression of intermediate

BDD nodes. In order to improve these algorithms to

substantially reduce the number of intermediate BDD

nodes, it is vital to search the state space in a struc-

tural and efﬁcient way. Here we introduce a simple

algorithm, Algorithm 3, which is formally deﬁned in

(Vahidi et al., 2006). The workset algorithm main-

tains a set of active disjunctive transition functions

. These active transition functions are selected one

at a time for the local reachability search. If there is

any new state found for the currently selected transi-

tion relation, then all of its dependent transition func-

tions (8) will be added in W

. Notice that in Algorithm

3, ”·” can be any event, since we don’t care about the

speciﬁc events as long as it is deﬁned in

) = {

| A

∈ D(A

)\{A

}} (8)

Algorithm 3: WorksetForwardReachbility.

1: input : Q

init

,.. .,

}

2: let W

:= {

,.. .,

},Q

:= Q

init

3: repeat

4: H : Pick and remove a transition

∈ W

5: k := k + 1

6: Q

:= Q

k−1

∪ { ´q | ∃q ∈ Q

k−1

(q,·) = ´q}

7: if Q

6= Q

k−1

then

8: W

:= W

k−1

∪ E(

)

9: end if

10: until W =

11: return Q

Selection Heuristics

In Algorithm 3, H denotes the heuristics of selecting

the next transition relation for the reachability search

such that the number of intermediate BDD nodes is

computed as small as possible. How a transition

is chosen among those in the working set W has great

inﬂuence on the performance of the algorithm. Here

we suggest a series of simple heuristics that have been

implemented and seem to work well on real-world

problems. In Section 6, those heuristics will be ap-

plied to a benchmark example to compare how they

inﬂuence the performance of the workset algorithm.

To ﬁnd a good heuristic, a two-stage selection rule

was implemented, see Fig.3. Using this method, a

complex selection procedure can be described as a

combination of two selection rules. In the current

implementation, the ﬁrst stage H1 selects a subset

⊂ W to be sent to H2 using one of the following

rules:

1. MaxF: Choose the automata with the largest de-

pendency set cardinality.

2. MinF: The opposite of above.

In case W

is not a singleton, the second stage H2 is

used to choose a single transition relation

among

. In the experiment, the following shown heuristics

can signiﬁcantly reduce the number of intermediate

BDD nodes for the simple problems.

1. Reinforcement learning (R) (Kaelbling et al.,

1996): Choose the best transition relation based

on the previous activity record.

2. Reinforcement learning + Tabu (RT) (Glover

and Laguna, 1997): Same as the reinforcement

learning with the difference that using tabu search

for the selection policy.

EFFICIENT SYMBOLIC SUPERVISORY SYNTHESIS AND GUARD GENERATION - Evaluating Partitioning

Techniques for the State-space Exploration

111

W’

Figure 3: The two stage selection heuristics for the workset

algorithm.

5 SUPERVISOR AS GUARDS

As mentioned in Section 1, given a supervisor repre-

sented as a BDD, it is cumbersome for the users to

relate each state to the corresponding BDD variables.

Therefore, it is more convenient and natural to rep-

resent the supervisor in a form similar to the original

models. In this section, an approach, the guard gen-

eration procedure which originates from (Miremadi,

2010), is discussed and combined with the BDD-

based disjunctive partitioning approach.

The guard generation procedure, being dependent

on three kinds of state sets (explained below), extracts

a set of conditional propositional formulae, referred to

as guards indicating under which conditions the event

can be executed without violating the speciﬁcations

and attaches them to the original models. In (Mire-

madi, 2010), the computation of the monolithic tran-

sition function is the prerequisite for generating these

state sets. Here an alternative way which is based on

the disjunctive partitioning approach is presented.

5.1 Computation of the Basic State Set

Concerning the states that are retained or removed af-

ter the synthesis process, the states that enable an ar-

bitrary event σ can be divided into three basic state

sets: forbidden state set, allowed state set and don’t

care state set.

The forbidden state set, denoted by Q

, is the set

of states in the supervisor where the execution of σ is

deﬁned for S

, but not for the supervisor. The allowed

state set, denoted by Q

, is the set of states in the

supervisor where the execution of σ is deﬁned for the

supervisor. In other word, for each event σ in S

’s

alphabet, Q

represents the set of states where event

σ must be allowed to be executed in order to end up

in states belonging to the supervisor.

In order to obtain compact and simpliﬁed guards,

inspired from the Boolean minimization techniques,

another set of states, denoted by Q

, which describes

a situation where executing σ will not impact the

result of the synthesis, is utilized to minimize the

guards.

Algorithms 4 and 5 presented below show how

to compute the forbidden states Q

and the allowed

states Q

by making use of the disjunctive transition

functions. Note that Q

and Q

denote the resultant

supervisor states and all the forbidden states yielded

from the synthesis algorithm in Section 4.1. The don’t

care state set, Q

can be deﬁned as the complement

of the union of Q

and Q

(9). The proof can be found

in (Miremadi, 2010).

= C(Q

∪ Q

) (9)

Algorithm 4: Compute Q

1: input : σ,Q

,.. .,

}

2: let Q

3: for all A

if σ ∈ Σ

4: Q

:= Q

∪ {q | ∃ ´q ∈ Q

(q,σ) = ´q}

5: end for

6: let Q

:= Q

∩ Q

7: return Q

Algorithm 5: Compute Q

1: input : σ,Q

,.. .,

}

2: let Q

3: for all A

if σ ∈ Σ

4: Q

:= Q

∪ {q | ∃ ´q ∈ Q

(q,σ) = ´q}

5: end for

6: let Q

:= Q

∩ Q

7: return Q

5.2 Guard Generation

Based on the basic state sets, some logic restrictions

can be extracted, expressing under which conditions

the events can be executed without violating the spec-

iﬁcations. For every automaton in the DES, a new

variable v is introduced to hold the current state of the

automaton. The following propositional function for

the event σ, G

: Q

×Q

×... ×Q

→ B, referred

to as guards, is deﬁned as:

,.. .v

i =







true hv

,.. .v

i ∈ Q

false hv

,.. .v

i ∈ Q

don

t care otherwise

(10)

where B is the set of Boolean values and v

rep-

resents the current state of automaton A

. In par-

ticular, σ is allowed to be executed from the state

,.. .v

i if the guard is true.

By applying minimization methods of Boolean

functions (utilizing the don’t care state set) and cer-

tain heuristics, the generated guards can be simpliﬁed.

The procedure is discussed in details in (Miremadi,

2010).

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

112

Table 2: Nonblocking and controllability synthesis.

Conjunctive Synthesis Disjunctive Synthesis

Model Reachable States Supervisor states BDD Peak Computation Time (s) BDD Peak Computation Time (s)

AGV 22929408 1148928 9890 6.50 2850 0.87

Parallel Man 5702550 5702550 12363 2.47 2334 1.57

Transfer line (1,3) 64 28 17 0.05 13 0.10

Transfer line (5,3) 1.07 × 10

8.49 × 10

2352 1.69 299 0.59

Transfer line (10,3) 1.15 × 10

6.13 × 10

31022 48.36 1257 3.89

Transfer line (15,3) 1.23 × 10

4.42 × 10

− − 3032 12.80

Cat&mouse (1,1) 20 6 43 0.02 31 0.05

Cat&mouse (1,5) 605 579 2343 0.08 273 0.09

Cat&mouse (5,1) 1056 76 848 0.30 305 0.30

Cat&mouse (5,5) 6.91× 10

3.15 × 10

− − 15964 20.86

∗

- denotes memory out.

6 CASE STUDIES

What we have discussed in the previous sections

has been implemented and integrated in the supervi-

sory control tool Supremica (

Akesson et al., 2003;

Akesson et al., 2006) which uses JavaBDD (Jav-

aBDD, 2007) as BDD package. In this section, the

implemented program will be applied to a set of rela-

tively complicated examples

. The examples are pre-

sented including references in the right column.

6.1 Benchmark Examples

A set of benchmark examples is brieﬂy described as

follows.

Automated Guided Vehicles

An AGV system, described in (Holloway and Krogh,

1990), is a simple manufacturing system where ﬁve

automated guided vehicles transport material between

stations. As the routes of the vehicles cross each

other, single-access zones are introduced to avoid col-

lisions.

Parallel Manufacturing Example

The Parallel Manufacturing Example, introduced in

(Leduc, 2002), consists of three manufacturing units

running in parallel. The system is modeled in three

layers in a hierarchical interface-based manner.

The Transfer Line

The Transfer Line TL(n,m), introduced as a tutorial

example in (Wonham, 1999), deﬁnes a very simple

The experiment was carried out on a standard Lap-

top (Core 2 Duo processor, 2.4 GHz, 2GB RAM) running

Ubuntu 10.04.

Figure 4: A single cell in the transfer line.

factory consisting of a series of n identical cells. Each

cell contains two machines and two buffers, one be-

tween the machines and one before a testing unit

which decides whether the work piece should be sent

back to the ﬁrst machine for further processing, or if

it should be passed to the next cell. Fig. 4 shows the

single cell in the transfer line. The capacity of each

buffer is m, which is usually chosen to be either 1 or

The Extended Cat and Mouse

An extended cat and mouse problem (Miremadi et al.,

2008), which is more complicated than the transfer

line model, generalizes the classic one presented in

(Ramadge and Wonham, 1987). The extended ver-

sion makes it possible to generate problem instances

of arbitrary size, where n and k denote the number of

levels and cats respectively.

6.2 Approach Evaluation

In this section, we evaluate the approach from two as-

pects. First, a comparison between two partitioning

techniques is made by analyzing the statistical data

from Fig. 2. In addition, the extended cat and mouse

example with multiple instances is utilized to investi-

gate how the choice of heuristics in the workset algo-

rithm inﬂuences the time efﬁciency.

Conjunctive vs. Disjunctive

Fig. 2 shows the result of applying two partitioning

techniques for the examples explained above. The

EFFICIENT SYMBOLIC SUPERVISORY SYNTHESIS AND GUARD GENERATION - Evaluating Partitioning

Techniques for the State-space Exploration

113

Table 3: Computing time for the nonblocking supervisor

with different heuristics.

Computation Time

(n,k) Workset(MaxF,R) Workset(MaxF,RT) Workset(MinF,R) Workset(MinF,RT)

(1,1) 0.04 0.06 0.05 0.05

(1,5) 0.30 0.27 0.33 0.36

(5,1) 0.08 0.08 0.09 0.08

(5,5) 3.15 2.90 3.85 3.42

(1,10) 0.67 0.66 0.75 0.73

(7,7) 21.4 17.6 25.5 22.9

(10,1) 0.23 0.20 0.24 0.23

(10,7) 100.3 88.5 136.4 138.0

supervisors synthesized for these examples are both

nonblocking and controllable and the safe states are

reachable. It is observed that both of the partitioning

based algorithms can handle the AGV and the Paral-

lel Manufacturing example, for which the number of

reachable states is up to 10

However, with DESs getting larger and more com-

plicated, the conjunctive partitioning technique is not

capable of synthesizing nonblocking and controllable

supervisors any more. The disjunctive partitioning,

on the other hand, could successfully explore the state

space within acceptable time. In addition, the column

”BDD Peak”, the maximal number of BDD nodes

during the reachability computation, in the ﬁgure,

shows that the disjunctive partitioning together with

heuristic decisions can effectively reduce the number

of intermediate BDD nodes.

Heuristics

Table 3 shows the computing time for synthesizing

the nonblocking supervisor from different instances.

Different combinations of heuristics, presented in

Section 4.3, are chosen to test the performance of

the workset algorithm. Empirically, for the models

with relatively large dependency sets, the heuristic

pair (MaxF,RT) seems to be a good choice, although

it hasn’t been formally proved. Observing the results

from Table 3, the workset algorithm can handle prob-

lem instances with either a large number of levels n

or cats k rather well. However, with both numbers

increasing, the computation time increases rapidly no

matter which heuristic pair is chosen.

7 CONCLUSIONS

In this paper, we improved and extended our previ-

ous work, the guard generation procedure, by apply-

ing an approach to efﬁciently performing symbolic

reachability exploration on composite discrete event

systems. More speciﬁcally, the content of the paper

can be summarized as follows:

1. Introduce the partitioning techniques to split the

BDD representation of δ

SpkP

into a set of smaller

but structural components.

2. To alleviate the problem that the intermediate

number of BDD nodes might still be huge dur-

ing the reachability exploration, we introduce the

workset algorithm together with a set of simple

heuristics to search the state-space in a structured

and efﬁcient way.

3. The guard generation procedure is tailored to

make use of the partitioned transition functions

and the synthesized supervisor to compute the ba-

sic state sets for an event.

4. The presented approach is applied to a set of

benchmark examples to be evaluated.

It is concluded that the disjunctive partitioning, with

appropriate heuristics, is suitable for solving large

modular supervisory control problems. There are sev-

eral directions towards which we could extend our ap-

proach. For instance, additional heuristics could be

applied to the workset algorithm, to further decrease

the number of intermediate BDD nodes. Moreover, it

is possible to combine with more sophisticated syn-

thesis techniques, such as compositional techniques,

to substantially improve the algorithm efﬁciency.

REFERENCES

Akers, S. B. (1978). Binary decision diagrams. IEEE Trans-

actions on Computers, 27:509–516.

Akesson, K., Fabian, M., Flordal, H., and Malik, R. (2006).

Supremica—an integrated environment for veriﬁca-

tion, synthesis and simulation of discrete event sys-

tems. In Proceedings of the 8th international Work-

shop on Discrete Event Systems WODES08, pages

384–385.

Akesson, K., Fabian, M., Flordal, H., and Vahidi, A. (2003).

Supremica—a tool for veriﬁcation and synthesis of

discrete event supervisors. In 11th Mediterranean

Conference on Control and Automation.

Aloul, F. A., Markov, I. L., and Sakallah, K. A. (2003).

Force: a fast and easy-to-implement variable-ordering

heuristic. In in ACM Great Lakes Symposium on VLSI,

pages 116–119.

Balemi, S., Hoffmann, G. J., Gyugyi, P., Wong-Toi, H., and

Franklin, G. F. (1993). Supervisory control of a rapid

thermal multiprocessor. IEEE Transactions on Auto-

matic Control, 38(7):1040–1059.

Bollig, B. and Wegener, I. (1996). Improving the vari-

able ordering of OBDDs is NP-complete. IEEE Trans.

Comput., 45(9):993–1002.

Bryant, R. E. (1992). Symbolic manipulation with ordered

binary decision diagrams. ACM Computing Surveys

24, 24:293–318.

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

114

Burch, J. R., Clarke, E. M., and Long, D. E. (1991). Sym-

bolic model checking with partitioned transition rela-

tions. In Proceedings of the International Conference

on Very Large Scale Integration, volume A-1 of IFIP

Transactions, pages 49–58. North-Holland.

Burch, J. R., Clarke, E. M., Long, D. E., Mcmillan, K. L.,

and Dill, D. L. (1994). Symbolic model checking

for sequential circuit veriﬁcation. IEEE Transactions

on ComputerAided Design of Integrated Circuits and

Systems, 13(4):401–424.

Byr

od, M., Lennartson, B., Vahidi, A., and

Akesson, K.

(2006). Efﬁcient reachability analysis on modu-

lar discrete-event systems using binary decision dia-

grams. In Proceedings of the 8th international Work-

shop on Discrete Event Systems, WODES’06, pages

288–293.

Cassandras, C. G. and Lafortune, S. (2008). Introduction to

Discrete Event Systems. Springer, 2nd edition.

Feng, L., Wonham, W. M., and Thiagarajan, P. S. (2007).

Designing communicating transaction processes by

supervisory control theory. Form. Methods Syst. Des.,

30(2):117–141.

Glover, F. and Laguna, M. (1997). Tabu search. Number 1

in Wiley-Interscience Series in Discrete Mathematics

and Optimization. Kluwer Academic Publishers.

Hoare, C. A. R. (1985). Communicating sequential pro-

cesses. Communications of the ACM, 21(8):666–677.

Holloway, L. E. and Krogh, B. H. (1990). Synthesis of feed-

back control logic for a class of controlled Petri Nets.

IEEE Transactions on Automatic Control, 35(5):514–

523.

JavaBDD (2007). available online.

Kaelbling, L. P., Littman, M. L., and Moore, A. W. (1996).

Reinforcement learning: a survey. Journal of Artiﬁcial

Intelligence Research, 4:237–285.

Leduc, R. J. (2002). Hierarchical interface-based supervi-

sory control. PhD thesis, Department of Electrical and

Computer Engineering, University of Toronto.

Miremadi, S. (2010). Symbolic Computation of Control

Functions Modeled by Automata with Variables. Li-

centiate thesis, Chalmers University of Technology,

Gothenburg, Sweden.

Miremadi, S.,

Akesson, K., Fabian, M., Vahidi, A., and

Lennartson, B. (2008). Solving two supervisory con-

trol benchmark problems using supremica. In Discrete

Event Systems, 2008. WODES 2008. 9th International

Workshop on, pages 131–136.

Ramadge, P. J. G. and Wonham, W. M. (1987). Supervisory

control of a class of discrete event processes. SIAM

Journal of Control and Optimization, 25(1):206–230.

Ramadge, P. J. G. and Wonham, W. M. (1989). The control

of discrete event systems. Proceedings of the IEEE,

77(1):81–98.

Shannon, C. E. and Weaver, W. (1949). The mathematical

theory of communication, volume 181. University of

Illinois Press.

Shoaei, M. R., Lennartson, B., and Sajed, M. (2010). Au-

tomatic Generation of Controllers for Collision-Free

Flexible Manufacturing Systems. In CASE 2010 6th

IEEE Conference on Automation Science and Engi-

neering, page 7.

Vahidi, A., Fabian, M., and Lennartson, B. (2006). Efﬁ-

cient supervisory synthesis of large systems. Control

Engineering Practice, 14(10):1157–1167.

Wonham, W. M. (1999). Notes on control of discrete event

systems. Technical report, University of Toronto.

EFFICIENT SYMBOLIC SUPERVISORY SYNTHESIS AND GUARD GENERATION - Evaluating Partitioning

Techniques for the State-space Exploration

115