AUTOMATIC FACE RECOGNITION

Methods Improvement and Evaluation

Ladislav Lenc and Pavel Kr´al

Department of Computer Science and Engineering, University of West Bohemia, Plzeˇn, Czech Republic

Keywords:

Face recognition, Self organizing maps, Eigenfaces.

Abstract:

This paper deals with Automatic Face Recognition (AFR), which means automatic identiﬁcation of a person

from a digital image. Our work focuses on an application for Czech News Agency that will facilitate to identify

a person in a large database of photographs. The main goal of this paper is to propose some modiﬁcations

and improvements of existing face recognition approaches and to evaluate their results. We assume that about

ten labelled images of every person are available. Three approaches are proposed: the ﬁrst one, Average

Eigenfaces, is a modiﬁed Eigenfaces method; the second one, SOM with Gaussian mixture model, uses Self

Organizing Maps (SOMs) for image reduction in the parametrization step and a Gaussian Mixture Model

(GMM) for classiﬁcation; and in the last one, Re-sampling with a Gaussian mixture model, several resize

ﬁlters are used for image parametrization and a GMM is also used for classiﬁcation. All experiments are

realized using the ORL database. The recognition rate of the best proposed approach, SOM with Gaussian

mixture model, is about 97%, which outperforms the “classic” Eigenfaces, our baseline, by 27% in absolute

value.

1 INTRODUCTION

Automatic Face Recognition (AFR) consists of au-

tomatic identiﬁcation of a person from a digital im-

age or from a video frame by a computer. It has

been the focus of many researchers during the past

few decades. AFR can be used in several applica-

tions: to facilitate access control to buildings; to sim-

plify the digital photo organization task; surveillance

of wanted persons; etc.

A huge amount of algorithms for face recogni-

tion were proposed. Most of them perform well un-

der certain “good” conditions (face images are well

aligned, the same pose and lighting conditions, etc.).

However, their performance is signiﬁcantly degraded

when these conditions are not accomplished. Many

methods have been introduced to handle these limi-

tations, but none of them perform satisfactorily in a

fully uncontrolled environment. AFR thus still re-

mains an open issue under general conditions.

The main goal of this paper is to propose some

modiﬁcations and improvements of existing face

recognition approaches. We would like to adapt ex-

isting methods to some particularities of our facial

ORL corpus: 1) the number of training examples are

strongly limited. However, this number is greater than

one training example; 2) the face pose

and the face

size (see Figure 1) may vary; 3) lighting conditions of

the images can also differ; 4) the time of acquisition

differs

. The recognition accuracy of the proposed

approaches will be evaluated and compared using the

ORL face database.

The outcomes of this work are designed to be used

by the Czech News Agency (

CTK) in the following

application.

CTK owns a large database (about 2 mil-

lions) of photographs. A signiﬁcant number of pho-

tos is manually annotated (i.e. the photo identity is

known). However, other photos are unlabelled; the

identities are thus unknown. The main task of our

application consists of the automatic labelling of the

unlabelled photos. This application must also han-

dle cases when one new photograph is added into the

database (automatic labelling of this picture). The

system must also guarantee the cases when the image

is not well aligned and its pose varies. Note that we

assume that about ten labelled images of every person

are available.

This paper is organized as follows. The next sec-

tion presents a short review of automatic face recog-

It means the face orientation to the camera

The images are taken in the interval of 2 years.

604

Lenc L. and Král P..

AUTOMATIC FACE RECOGNITION - Methods Improvement and Evaluation.

DOI: 10.5220/0003182206040608

In Proceedings of the 3rd International Conference on Agents and Artiﬁcial Intelligence (ICAART-2011), pages 604-608

ISBN: 978-989-8425-40-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

nition. Section 3 describes the different methods we

propose. Section 4 gives experimental results of our

methods. In the last section, we discuss the research

results and we propose some future research direc-

tions.

2 SHORT REVIEW OF FACE

RECOGNITION APPROACHES

Early face recognition approaches were based on

normalized error measures between signiﬁcant face

points. One of the ﬁrst method was designed by Bled-

soe (Bledsoe, 1966). Coordinates of important face

points were manually labelled and stored in the com-

puter. The feature vector was composed of the dis-

tances between these points. Vectors were classiﬁed

by the Nearest Neighbour rule. The main drawback

of such methods is the need of manually labelling of

important face points. On the other hand, variations

of the face pose, lighting conditions and other factors

can be handled due to this manual marking. Another

fully automatic method using similar measurements

was designed by Kanade (Kanade, 1977). In this case,

the labelling of important face points is automatic.

One of the ﬁrst successful approaches is Prin-

cipal Component Analysis (PCA), so called Eigen-

faces (Turk and Pentland, 1991). Eigenfaces is a sta-

tistical method that takes into account the whole im-

age as a vector. Image vectors are put together and

create a matrix. Eigenvectors of this matrix are cal-

culated. Face images can then be expressed as a lin-

ear combination of these vectors. Each image is rep-

resented as a set of weights for corresponding vec-

tors. Eigenfaces perform very well when images are

well aligned and have approximately the same pose.

Changing lighting conditions, pose variations, scale

variations and other dissimilarities between images

decrease the recognition rate rapidly (Sirovich and

Kirby, 1987).

Another group of approaches use Neural Net-

works (NNs). Several NNs topologieswere proposed.

One of the best performing methods based on neu-

ral networks is presented in (Lawrence et al., 1997).

Image is ﬁrst sampled into a set of vectors. Vectors

created from all labelled images are used as a train-

ing set for a Self Organizing Map (SOM). Image vec-

tors of the recognized face are used as an input of the

trained SOM. Output of the SOM is then used as an

input of the classiﬁcation step, which is a convolu-

tional network. This network has a few layers and

ensures some amount of invariance to face pose and

scale.

A frequently discussed type of face recognition

algorithms is elastic bunch graph matching (Wiskott

et al., 1999; Bolme, 2003). This algorithm is based

on Gabor Wavelet ﬁltering. Feature vectors are cre-

ated from Gabor ﬁlter responses as signiﬁcant points

in the face image. Bunch graph is created and is

consequently matched against the presented images.

Another method which utilizes Gabor wavelets is the

method proposedby Kepenekci in (Kepenekci, 2001).

It uses wavelets in a different manner. Fiducial points

are not ﬁxed. Their locations are assumed to be at the

maxima of Gabor ﬁlter responses. The main advan-

tage of Gabor wavelets is some amount of invariance

to lighting conditions.

3 METHODS DESCRIPTION

3.1 Average Eigenfaces

A classic Eigenfaces approach uses only one training

image. Our contribution is to adapt this method for

the case of more training examples being available.

We create one reference example from all training im-

age samples. In this preliminary study, we compute

from all training examples an average value of the in-

tensity at each pixel. These images are used for prin-

cipal component analysis.

3.2 SOM with a Gaussian Mixture

Model

Current face recognition methods are composed

of two steps: parametrization and classiﬁcation.

Parametrization is used to reduce the size of the origi-

nal image with the minimal loss of discriminating in-

formation. The parametrized image is then used for

classiﬁcation step instead of the original one.

We use self organizing maps in the parametriza-

tion step in order to reduce the size of the feature

vectors. The second step is a classiﬁcation by the

Gaussian mixture model. The use of the SOM in the

parametrization is motivated by the work proposed

in (Lawrence et al., 1997). Authors use also SOMs

in the ﬁrst step, while the classiﬁcation model differs.

3.2.1 Parametrization with a SOM

Input images are represented as two dimensional ar-

rays of pixel intensities. We consider grayscale pic-

tures where each pixel is represented by a single in-

tensity value. Each image can be also seen as a sin-

gle dimensional vector of size w ∗ h, where w and h

are image width and height, respectively. For the di-

mension reduction a self organizing map is used. The

AUTOMATIC FACE RECOGNITION - Methods Improvement and Evaluation

605

image is ﬁrst sampled and a set of vectors is created

by the following way. A rectangular sliding window

is used.

The sampling procedure uses a rectangular sliding

window which scans over the image. At each posi-

tion, a vector containing intensity values of pixels, is

created. The size of the created vector is l = ww∗wh,

where ww an wh are window width and height, re-

spectively. The vectors obtained from all images are

used as a training set for self organizing map. The

trained SOM (standard SOM training algorithm) is

then used for image parametrization. Each input vec-

tor is associated with the closest node of the SOM and

its position is used to compute the resulting parameter

vector. Values of this vector are created as an average

value of the node vector associated with this position.

The vectors are used as an input for the classiﬁcation

step.

3.2.2 Classiﬁcation with a GMM

Let us call F the set of featuresfor one image obtained

in the parametrization step, let I be the face image.

We use a GMM classiﬁer that computes P(F|I). The

recognized image is then:

I = argmax

P(I|F) = argmax

P(F|I)P(I) (1)

We assume all images to be equiprobable. The prior

probability P(I) can be thus removed from the equa-

tion.

3.3 Re-sampling with a Gaussian

Mixture Model

An alternative way to reduce the feature space is im-

age re-sampling. Image size is reduced using the re-

size ﬁlters from ImageMagick library

. Intensity val-

ues of the resulting images are directly used as image

vectors. These vectors are classiﬁed by a GMM in the

same way as in the previous case.

Different resize ﬁlters and the different sizes of

the resulting output vectors are evaluated. The four

ones are interpolated ﬁlters, while the last one, Cubic

ﬁlter, is a Gaussian ﬁlter. The ﬁrst method, a Point

ﬁlter, determines the closest point in the original im-

age to the new pixels position and uses its intensity

value in the resized image. The Box ﬁlter computes

an average value of the pixels placed in the ”box” (a

rectangular window of a deﬁned size). The next eval-

uated ﬁlter a Triangle ﬁlter. This ﬁlter takes into ac-

count the distances of the pixels and uses a weighted

average instead of just an average value. Hermite ﬁl-

ter has similar results as the triangle ﬁlter, but pro-

duces a smoother round off in large scale enlarge-

ments. More information about resize ﬁlters is avail-

able at ImageMagick website

4 EXPERIMENTAL SETUP

4.1 Corpus

The ORL database which was created in AT & T

Laboratories

is used to evaluate the proposed ap-

proaches. The pictures of 40 individuals were taken

between April 1992 and April 1994. For each per-

son 10 pictures are available. Every picture contains

just one face. They may vary due to three follow-

ing factors: 1) time of acquisition; 2) head size and

pose; 3) lighting conditions. The images have black

homogeneous background. The size of pictures is

92 × 112 pixels. Further description of this database

is in(Gross, 2005). Figure 1 shows two examples of

one individual.

All experiments except the classic Eigenfaces

approach are realized using a cross-validation pro-

cedure, where 10% of the corpus is reserved for the

test, and another 10% for the development set.

Figure 1: An example of faces from ORL database

4.2 Experiments

We chose a “classic” Eigenfaces as a baseline for

our experiments. A slightly modiﬁed cross-validation

procedure is used in this case. 10% of the corpus is

still reserved for the test. However for the training,

we use only one example from the training pool. All

training examplesare subsequently used. Recognition

error rate of this approach is shown in the ﬁrst section

of Table 1.

4.2.1 Average Eigenfaces

For creation of the average images ten images of each

person are used. The second section of Table 1 shows

http://www.cl.cam.ac.uk/research/dtg/attarchive/

facedatabase.html

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

606

the recognition error rate of this approach. Unfor-

tunately, the error rate of the proposed approach is

higher than the baseline. It is probably due to the

computation of an average of the image factors in the

ORL database (see Section 4.1). We assume that the

recognition rate will be better when the above men-

tioned factors are closer.

4.2.2 Parametrization with a SOM

Original images in ORL database have a size of

92× 112 pixels. A square window of dimension 5× 5

is used for image sampling. This window is moved

by 4 pixels, the overlap is thus 1 pixel. In the sam-

pling step 644 vectors of the size of 25 are created

for every image. These vectors are used to train the

two dimensional self organizing map. Then vectors

from each image are classiﬁed by the trained SOM.

For every vector a resulting value is determined as an

average value of the closest node vector. Therefore,

a vector of the size of 644 is created for every image.

These vectors are classiﬁed by a GMM with 2 Gaus-

sian mixtures.

The third section of Table 1 shows the recogni-

tion error rate of some sizes of the SOM. Several

SOM topologies are evaluated. However, only the

four best ones are reported in this table. All recogni-

tion scores are very high and outperform signiﬁcantly

all previously described approaches. The recognition

error rate is reduced to 3.75%. This table also shows

that the size of the SOM is an important clue for face

recognition.

Table 1: Automatic face recognition error rate for different

parametrization/classiﬁcations methods.

Method Error rate

1. Eigenfaces 30.85

2. Average Eigenfaces 53.88

3. SOM & GMM

SOM size Error rate

8x8 4,5

10x10 3,75

12x12 3,25

14x14 3,75

Two level Dimension Reduction. In this experiment,

we would like to evaluate the relation between the re-

duction of the parametrized input vector and the loss

of the recognition accuracy. This means to determine

the minimal feature vector without a signiﬁcant de-

crease of the performance of our system.

Another SOM is used for this additional vector

reduction in a similar way as in the previous case.

Several SOM topologies are also evaluated. Table 2

shows the recognition rate of this experiment. The re-

sults are not as good as in the previous case, but still

signiﬁcantly better than our baseline. The best recog-

nition rate is obtained with the SOM topology 10×10

neurons with a vector size 42.

Table 2: Error rates for for two level dimension reduction

with different SOM sizes.

1 level 1 SOM size 2 level SOM size Error rate

10x10 8x8 14,25

12x12 10x10 10,25

4.2.3 Parametrization by Re-sampling

Table 3 shows recognition rates for different ﬁlters

and different image sizes. This table shows that all

ﬁlters are almost comparable except the Point ﬁlter.

The worst recognition score of this ﬁlter is probably

due to its simplicity. Moreover, the best recognition

rate is obtained by the vector of size of 8× 8. We can

conclude that the recognition accuracy of this experi-

ment is close to the previous one with one level SOM

parametrization.

Table 3: Comparison of the recognition error rate of differ-

ent resize ﬁlters and different parametrized vector size with

a GMM classiﬁer

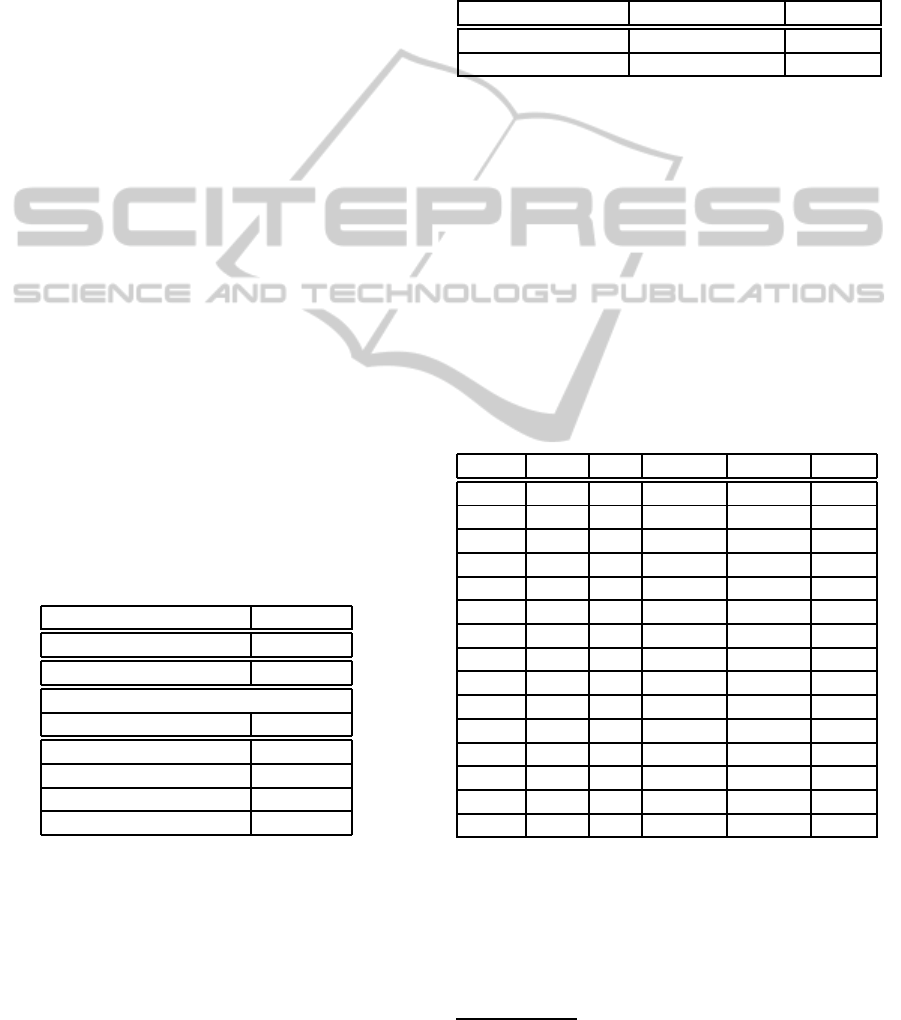
Filter Point Box Triangle Hermite Cubic

2x3 55 40 39,75 38 40,75

3x4 44,75 13,5 16 14 17,75

5x6 20,75 6,25 5 5,25 6,5

6x7 18,5 3,25 3 3 4

7x8 12,5 3,25 3,25 4,5 4

8x10 7,75 2,25 3 2,75 2,5

9x11 5 2,5 2,75 2,75 2,75

10x12 5,25 3 2,75 3,5 3

11x13 5,25 3 3 3,25 3,5

13x16 3,75 3,25 3,5 4 3,75

15x18 3,75 3,75 3,5 4 3,5

17x21 4 4 3,75 4,5 3,75

19x23 4 4,5 4,75 4,25 4,5

21x26 4 3,75 3,75 4 3,75

23x28 4,25 4,5 4,25 4,75 3,75

5 CONCLUSIONS

In this paper, three methods for automatic face recog-

nition are proposed. The recognition accuracy is eval-

uated on the ORL database. Experiments show that

http://www.imagemagick.org/Usage/resize/

AUTOMATIC FACE RECOGNITION - Methods Improvement and Evaluation

607

the ﬁrst approach, an Average Eigenfaces, does not

perform well and it is thus not a good further re-

search direction. However,the two other proposed ap-

proaches, namely SOM with Gaussian mixture model

and Resampling with a Gaussian mixture model, have

very good recognition accuracy. Their recognition er-

ror rate is close to 3%, which outperforms the “clas-

sic” eigenfaces, our baseline, by 27% in absolute

value. Moreover, these scores are also slightly higher

than those reported in (Lawrence et al., 1997) and

in (Kepenekci, 2001). The authors use also ORL

database but different approaches.

The ﬁrst perspective consists of the evaluation of

the proposed methods on larger corpora (i.e. the

CTK

database). We would like also to use another classi-

ﬁer such as Dynamic Bayesian Networks. The last

perspective consists of the combination of classiﬁers

in order to improve the recognition accuracy of the

separate models.

ACKNOWLEDGEMENTS

This work has been partly supported by the Ministry

of Education, Youth and Sports of Czech Republic

grant (NPV II-2C06009).

REFERENCES

Bledsoe, W. W. (1966). Man-machine facial recognition.

Technical report, Panoramic Research Inc., Palo Alto,

CA.

Bolme, D. S. (2003). Elastic Bunch Graph Matching. PhD

thesis, Colorado State University.

Gross, R. (2005). Face Databases. Springer-Verlag.

Kanade, T. (1977). Computer recognition of human faces.

Birkhauser Verlag.

Kepenekci, B. (2001). Face Recognition Using Gabor

Wavelet Transform. PhD thesis, The Middle East

Technical University.

Lawrence, S., Giles, S., Tsoi, A., and Back, A. (1997).

Face recognition: A convolutional neural network ap-

proach. IEEE Trans. on Neural Networks.

Sirovich, L. and Kirby, M. (1987). Low-dimensional proce-

dure for the characterization of human faces. Journal

of the Optical Society of America, 4.

Turk, M. A. and Pentland, A. P. (1991). Face recognition us-

ing eigenfaces. Computer Vision and Pattern Recog-

nition.

Wiskott, L., Fellous, J.-M., Kr¨uger, N., and von der Mals-

burg, C. (1999). Face recognition by elastic bunch

graph matching. Intelligent Biometric Techniques in

Fingerprint and Face Recognition.

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

608