EVALUATING RERANKING METHODS USING WIKIPEDIA

FEATURES

Koji Kurakado

Graduate School of Information Science and Electrical Engineering, Kyushu University, Fukuoka City, Fukuoka, Japan

Tetsuya Oishi

†

, Ryuzo Hasegawa

‡

, Hiroshi Fujita

‡

, Miyuki Koshimura

‡

†

Research Institute for Information Technology, Kyushu University, Fukuoka, Japan

‡

Faculty of Information Science and Electrical Engineering, Kyushu University, Fukuoka, Japan

Keywords:

Wikipedia, Reranking, Link analysis.

Abstract:

Many people these days access a vast document on the Web very often with the help of search engines such as

Google. However, even if we use the search engine, it is often the case that we cannot ﬁnd desired information

easily. In this paper, we extract related words for the search query by analyzing link information and category

structure. we aim to assist the user in retrieving web pages by reranking search results.

1 INTRODUCTION

In recent years, many people got possible to access

Web very easily thanks to the vast spread of internet

as well as the availability of convenient search en-

gines. For instance, Google

,Yahoo

are commonly

used. Given a few keywords, these systems retrieve

such Web pages that users want to see from among

the huge databases residing on the internet. Google,

in particular, successfully presents us the most suit-

able pages on the ﬁrst page of the retrieval results by

applying the PageRank algorithm (Page et al., 1998)

which evaluates relevance of pages based on page

links.

Nevertheless, since the Web sources are so enor-

mous and constantly increasing, it is often the case

that we are not satisﬁed with the results given by

them. To solve the problem, we propose reranking

methods based on Wikipedia. Wikipedia attracts at-

tention on the ﬁeld of NLP and Data-Mining, because

of its impressive characteristics.

We implement a reranking system that extracts re-

lated words from a given search query. The system

uses Wikipedia’s link information and category struc-

tures.

Wikipedia is a Wiki-based huge Web encyclope-

dia. As a corpus for knowledge extraction, Wikipedia

http://www.Google.co.jp/

http://www.Yahoo.co.jp/

has several useful features. Thus, there have been var-

ious Wikipedia studies.

Semantic relatedness measurement is one of

the most major Wikipedia studies. Strube and

Ponzetto (Ponzetto and Strube, 2006) were the ﬁrst

to compute measures of semantic relatedness using

Wikipedia. Their approach uses the category hier-

archy of Wikipedia. Gabrilovich and Markovitch

(Gabrilovich and Markovitch, 2007) proposed the Ex-

plicit Semantic Analysis (ESA) method. ESA rep-

resents the meaning of texts in a high-dimensional

space of concepts derived from Wikipedia page. The

semantic relatedness between two words is com-

puted by the cosine similarity between the two vec-

tors. They achieve the most accurate results using

the gWordSimilarity-353 test collectionh (Finkelstein

et al., 2002). Witten and Milne (Witten and Milne,

2008) proposed a new method based on link co-

occurrence. Although the accuracy of this approach

is a little worse than ESA, it requires far less data

and resources. Chernov et al. (Chernov et al., 2006)

extracted a category set by using links that direct to

or refer to pages included in categories. According

to their results, inlinks have superior performance in

comparison to outlinks.

Researches that try to extract useful knowledge

from Wikipedia are called ”Wikipedia Mining” by

Japanese researchers. Nakayama et al. (Nakayama

et al., 2007) proposed a method, named pﬁbf, to com-

376

Kurakado K., Oishi T., Hasegawa R., Fujita H. and Koshimura M..

EVALUATING RERANKING METHODS USING WIKIPEDIA FEATURES.

DOI: 10.5220/0003183003760381

In Proceedings of the 3rd International Conference on Agents and Artiﬁcial Intelligence (ICAART-2011), pages 376-381

ISBN: 978-989-8425-40-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

pute related words by analyzing the link structure of

Wikipedia pages. They construct a huge scale associ-

ation thesaurus. Ito et al. (Ito et al., 2008) proposed

the method that constructs an association thesaurus,

too. Their approach computes semantic relatedness

by using link co-occurrence. They mention that the

method is more scalable than pﬁbf in spite of their

high accuracy close to that of pﬁbf. The method is

similar to Milne’s in that they use co-occurrence. Al-

though the accuracy of this method is a little worse

than Milne’s, we consider the comparison should be

made in the same environment. So, we cannot say

that one is better than the other.

Nakayama et al. (Nakatani et al., 2009) pro-

posed an evaluation method of search results by an-

alyzing the link information and category structure of

Wikipedia. They extract a category domain of query

and evaluate search results by using terms included

in the domain. Hori et al. (Hori et al., 2010) use

Wikipedia as a source for query expansion.

2 RERANKING WEB SITES

In this section, we describe our reranking methods

based on Wikipedia. We calculate the evaluation

value for each site to which the search engine returns.

Then we rerank the search result in descending order

according to the evaluation value.

We select four features from Wikipedia for rerank-

ing: inlink, outlink, link co-occurrence, category.

Here we propose a web page evaluation method that

uses each of the above features.

An inlink of a Wikipedia page is a link pointing to

that particular page. An outlink of a Wikipedia page

is a link from that particular page to other page. For

example, If page A contains a link directing to page

B, A has an outlink to B, and B has an inlink from A.

In the following, we ﬁrst show an approach that

expands the category a search query belongs to. We

consider not only the categories a query belongs to but

also those related to the original categories as a cate-

gory set for the query. Second, we explain the web

page evaluation model that uses each of the features.

2.1 Expanding Categories to which a

Query Belongs

A Wikipedia page belongs to one or more categories.

In addition, unlike a thesaurus such as WordNet, the

category structure of Wikipedia is not just hierarchi-

cal. It can be thought of as consisting of overlapping

trees.

Nakayama et al. consider that they cannot get

enough information from the category that the query

originally belongs to. So, they regard the categories

that contain a lot of inlinks to the query as those the

query belongs to.

Suppose that c is a Wikipedia category and size(c)

is the total number of pages belonging to c. In addi-

tion, the number of pages in c from which the query

has inlinks is expressed as in(c). CScore

ﬁned as follows:

CScore

in(c)

size(c)

(1)

We also use the technique that expands the cate-

gory a query belongs to. Moreover, we propose the

methods that uses outlink, link co-occurrence, or a

category structure.

Expanding Categories based on Outlink

The method using outlink is very simple. We re-

gard the categories that contain a lot of outlinks to the

query as those the query belongs to. Thus, the score

CScore

out

CScore

out

where out(c) is the number of pages in c to which the

query has outlinks.

Expanding Categories based on Link

Co-occurrence

Thinking simply, link co-occurrence means that link

A and link B appear in the same page. However, two

links co-occur if they appear in a window of K sen-

tences (window K in short).

Meanwhile, Wikipedia has the hierarchical para-

graph from level2 to level4. For example, the

Wikipedia page of “Computer” has level2 paragraph

“Function”. And level3 paragraphs “Control unit”

and “Memory” belong to “Function”.

Thus, we proposed three methods as follows:

1. Two links co-occur if they appear in the same

page.

2. Two links co-occur if they appear in a window K.

3. Two links co-occur if they appear in the same

paragraph whose level is highest and that contains

more sentences than a window K.

Now, we show an example of the third method.

Suppose that the size K of a window is 10 , the page

of “Computer” contains 100 sentences , paragraph

“Function” contains 15 sentences, paragraph “Mem-

ory” contains 5 sentences and that there is an inlink to

“DRAM” in paragraph “Memory”.

EVALUATING RERANKING METHODS USING WIKIPEDIA FEATURES

377

First, we look at paragraph “Memory” with the

highest level. Then, since the number of sentences

of paragraph “Memory” is less than that of a window

K, we look at paragraph “Function”, whose level is

one higher than “Memory”. Since the number of sen-

tences of “Function” is larger than that of a window

K, the links in “Function” co-occur with “DRAM”.

The score CScore

CScore

co(c)

size(c)

(3)

where co(c) is the number of pages in c that co-occur

with the target page of a query.

Expanding Categories based on Category Tree

On the category tree of Wikipedia, the categories in

a near position have high relevance each other. Thus,

we calculate the score CScore

cat

CScore

cat

length(c)

(4)

where length(c) is the number of paths from c to the

category a target page of query belongs to. We calcu-

late length(c) only about the categories c

the query

belongs to, and parent categories of c

, and children

categories of c

, and the categories that have common

parents with c

2.2 Web Site Evaluation based on

Wikipedia Features

We evaluate web sites using the entries of Wikipedia

included in the web sites. We compute a level ex-

pressing how much each entry of Wikipedia is re-

lated to the query according to the model that uses

Wikipedia features. When a site includes a lot of

highly related entries, we consider the site is im-

portant. The evaluation method based on the hy-

pothesis that Wikipedia is a reliable corpus and the

Wikipedia’s entries closely related with query is im-

portant.

When a web site contains the entries of Wikipedia

w(s) = {t

,. .. ,t

}, the score SiteScore(s) is calcu-

lated as follows:

SiteScore(s) =

∑

t∈w(s)

Score(t) (5)

where Score(t) is a related level of the Wikipedia’s

entry t with the query q. It is calculated according to

the model described next.

Calculating a Score based on Inlink

The score calculated by using inlink Score

(p) is cal-

culated as follows:

Score

(p) =

inlink(p)

linknum(p)

(6)

where inlink(p) is the number of inlinks from a page

of Wikipedia p to query q. linknum(p) is the total

number of links included in p.

Calculating Scores based on Outlink

To do this, we consider two cases as follows:

(1) based on TF-IDF

(2) based on the vector of TF-IDF

The score of (1), Score

outt fid f

(p), is calculated as fol-

lows:

Score

outt fid f

(p) =

outlink(p)

linknum(q)

· log

|W|

|P|

(7)

where outlink(p) is the number of outlinks from

query q to a page of Wikipedia p. |W| is the total

number of links in Wikipedia. |P| is the document

frequency of the entry of Wikipedia p.

Next, the method (2) is used by (Witten and Milne,

2008; Nakayama et al., 2007). Calculating TF-IDF in

a page, they extract a vector of weighted links. Af-

ter extracting the vectors for each page, relatedness

between two pages can be calculated comparing their

vectors by using cosine metrics. Thus, the score of

(2), Score

outt fid fvec

(p), is calculated as follows:

Score

outt fid fvec

(p) =

∑

k=1

∑

k=1

∑

k=1

(8)

where v

= {l

,. .. ,l

} is the vector of page p.

Calculating Scores based on Link Co-occurrence

To do this, we consider three cases as follows:

(1) using cosine metrics

(2) using the second-order co-occurrence (Schutze

and Pedersen, 1997)

(3) based on Normalized Google Distance (Cilibrasi

et al., 2007)

The score of (1), cooOccur(p), is calculated as

follows:

Score

cocos

cooOccur(p)

f(p) · f(q)

(9)

where f (p) is the term frequency of a page p.

cooOccur(p) is the number of pages that co-occur

with the target page of a query.

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

378

Next, the method (2) is used by (Ito et al.,

2008). They create a vector of link ﬁrst-order co-

occurrence. A ﬁrst-order co-occurrence is calculated

like cooOccur(p) by cosine metrics . vi, which is

the link vector of page p, is deﬁned by the following

formula: v

= {c

,. .. ,c

} where c

is a ﬁrst-

order co-occurrence between page p and i. Thus, the

score of (2) Score

cocosvec

(p) is calculated as follows:

Score

cocosvec

(p) =

∑

k=1

∑

k=1

∑

k=1

(10)

The method (3) is used by (Witten and Milne,

2008). They use Normalized Google Distance model.

Thus, the score of (3) Score

congd

(p) is calculated as

follows:

Score

congd

(p) =

log(max(|P|,|Q|)) − log(|P∩ Q|)

log(|W|) − log(min(|P|,|Q|))

(11)

where |P∩ Q| is the number of a page including both

the links of p and q.

Calculating Scores based on Category

To do this, we consider two cases as follows:

(1) using a set of categories to which the original

query belongs

(2) using a set of categories that are expanded by the

method described in section 3.1.

The score of (1), Score

cat

(p), is calculated as follows:

Score

cat

(p) =

∑

c∈C

set

(q)

b(p,c)

size(c)

(12)

whereC

set

(q) = { c

,. .. ,c

} is the set of categories

to which a query originally belongs. b(p,c) is a

Boolean value. If a page p belongs to a category c,

b(p,c) becomes 1. Otherwise, b(p,c) becomes 0.

Next, the score of (2), Score

catex

(p), is calculated

as follows:

Score

catex

(p) =

∑

c∈C

setex

(q)

b(p,c) ·CScore(c)

size(c)

(13)

where C

setex

(q) is the top K categories in descending

order of CScore(c).

3 EXPERIMENTS

In this section, we evaluate and compare our methods

in terms of their performance in improving the search

results for the initial query.

We used the Japanese Wikipedia database dump

from 28 March 2010 in our experiment. We also

use “Google Japanese search” in our experiment. We

asked 6 evaluators to make 51 queries that contain at

least one entry of Wikipedia and goals. They consist

of 17 queries with at most three words for each. In

addition, if the query contains a word which appears

in disambiguation pages, we ask evaluators to select a

concept. Next, we evaluated 100 web sites on a scale

of 1 to 4 as follows: 4:“Highly relevant”, 3:“Rele-

vant”, 2:“Partially relevant” and 1:“No relevant”.

We remove web sites that do not contain more

than 50 entries of Wikipedia from search results.

Many sites that we remove are the html documents

that we fail to parse. As a result, the average number

of the search results become 93.86 sites. While the

average number of sites evaluated as 3 or 4 is 18.02,

the average number of sites evaluated as 4 is 6.34.

Moreover, even if a site contains 500 or more entries

of Wikipedia, we analyze up to 500 words in the site

so that a long document does not have an advantage.

The accuracy of the results is measured by preci-

sion at K, and MAP (Mean Average Precision). Pre-

cision at K is precision of top K results. K is set to 10

in this experiment. MAP is an average of AP(Average

Precision). AP is the average of ratios of the number

of documents that user judges relevant to the num-

ber of whole given documents. Since these evaluation

methods require that a documents is either relevant or

irrelevant, we calculate both results for the strict rel-

evance that we regard 4 as relevant and the relaxed

relevance that we regard 3 and 4 as relevant.

4 RESULTS AND DISCUSSION

We have proposed several methods in section 3. In

this section, we ﬁrst evaluate category expansion

methods. Second, we evaluate methods based on

Wikipedia features. Finally, we compare our methods

with Google search results. When we evaluate a com-

bination of each method, we normalize each vector

according to cosine normalization and add vectors.

Evaluation of Category Expansion Methods. Table

1 shows the results of category expansion methods in

section 3.1. Where P@10 is the result for precision

at K with the relaxed relevance (3 + 4). P@10

and

MAP

are the results for the strict relevance (4). The

window size of link co-occurrence is set to 10. Here,

we use the top 20 categories in descending order of

score. Query in Table 1 is the method using a set of

categories to which a query originally belongs.

In comparison with other methods that use only

a single feature, outlink method is more accurate. In

addition, the co-occur method using paragraph per-

formed less accurately than the method using sen-

EVALUATING RERANKING METHODS USING WIKIPEDIA FEATURES

379

tence. Since we count all words in a paragraph that

contains K and more sentences, there is the varia-

tion of the number of the co-occurrence links among

pages. Moreover, the variation gives bad inﬂuence in

the result.

It also shows that a combination of outlink and

category is the best accurate method. Outlink

achieves good results, while global information of

category improves the outlink method. Since the

method is more accurate than a method using a set of

categories to which a query originally belongs , cate-

gory expansion methods are effective.

Table 1: P@10 and MAP : category expansion methods.

P10 P10 H MAP MAP H

query 0.284 0.109 0.310 0.17

inlink 0.29 0.121 0.315 0.19

outlink 0.304 0.128 0.325 0.196

co-occur(all) 0.265 0.105 0.288 0.167

co-occur(sentence) 0.281 0.109 0.3 0.172

co-occur(paragraph) 0.273 0.104 0.296 0.167

outlink+category 0.306 0.122 0.329 0.197

Evaluation of the Methods based on Wikipedia

Features. Table 2 shows the results of our methods

using each Wikipedia feature in section 3.3. Where

count is the average number of related words ex-

tracted from Wikipedia. Category in Table 2 corre-

sponds to the method of expanding categories using

outlink and category information. In comparison with

other single methods, it identiﬁes outlink as the more

accurate measure, too. This result demonstrates that

the complicated methods and methods of using a lot

of information are bad. For example, the second or-

der link co-occurrence method and the TF-IDF vector

method are worse than simple methods. Thus it re-

veals that the number of related words does not reﬂect

accuracy and deeply related words are very important.

Next, the result shows that a combination of out-

link and category or link co-occurrence is the best

accurate method. So, global information of cate-

gory or link co-occurrence would improve the outlink

method.

Comparison of our Methods with Google. Table 3

shows the results of Google and our methods. Our

methods are considerably worse than Google search

results. However, precision score of the search result

is 18.02/93.86= 0.192. Thus, our method is effective

in comparison with the case when we select sites at

random.

Table 4 shows the results of Google and our meth-

ods when we use only one word query. The aver-

age number of the search results become 91.28 sites.

While the average number of sites evaluated as 3 or

Table 2: P@10 and MAP : the methods based on Wikipedia

features.

P@10 P@10 H MAP MAP H count

category 0.306 0.122 0.329 0.197 4433

inlink 0.301 0.127 0.321 0.208 804

outlink

(tﬁdf) 0.31 0.129 0.334 0.222 143

outlink

(tﬁdfVec) 0.301 0.126 0.318 0.2 83694

co-occur

(cosine) 0.299 0.121 0.318 0.192 6271

co-occur

(second) 0.267 0.108 0.283 0.159 166867

co-occur

(NGD) 0.284 0.119 0.297 0.179 6271

outlink

+category 0.318 0.133 0.344 0.224 4521

outlink 1+co-occur 1 0.321 0.136 0.342 0.225 6321

Table 3: P@10 and MAP : Google and our methods.

P@10 P@10 H MAP MAP H

outlink 1 0.31 0.129 0.334 0.222

outlink 1+category 0.318 0.133 0.344 0.224

outlink 1+co-occur 1 0.321 0.136 0.342 0.225

Google 0.494 0.239 0.505 0.417

Table 4: P@10 and MAP : Google and our methods when

we use only one word query.

P@10 P@10 H MAP MAP H

category 0.355 0.15 0.373 0.262

outlink 1 0.347 0.157 0.38 0.314

outlink 1+category 0.365 0.167 0.394 0.311

outlink 1+co-occur 1 0.382 0.172 0.394 0.312

Google 0.439 0.231 0.477 0.474

more is 15.88, the average number of sites evaluated

as 4 is 6.03.

Compared with the case where all queries are

used, it is a very good result. The reason for this is

that our methods have some difﬁculty to recognize

deep semantic relationship between different words

in a query unless the relationship is apparent or very

strong. For example, given a query like “C++, Java”,

our methods works well. But, given a query like

“iPod, backup”, the methods do not work well.

On the other hand, precision score of the search

result is 15.88/91.28 = 0.174. Thus, our method is

quite effective in comparison with the case when we

select sites at random. But our method was worse than

Google search result.

Figure 1 shows the graphs of the results. We con-

centrate on how much the accuracy of the retrieval

results is improved compared to those obtained by an

existing engine. First, we calculate AP for the results

given by Google. Next, each query is classiﬁed into

10 classes according to the value of AP, ﬁrst 0, sec-

ond 0.1 or less, and so on, and ﬁnally 1.0 or less.

Then, we calculate MAP for each class of queries and

for each method being compared. Each MAP value

of the point where AP is less than 0.2 represents the

accuracy of each method when using the queries for

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

380

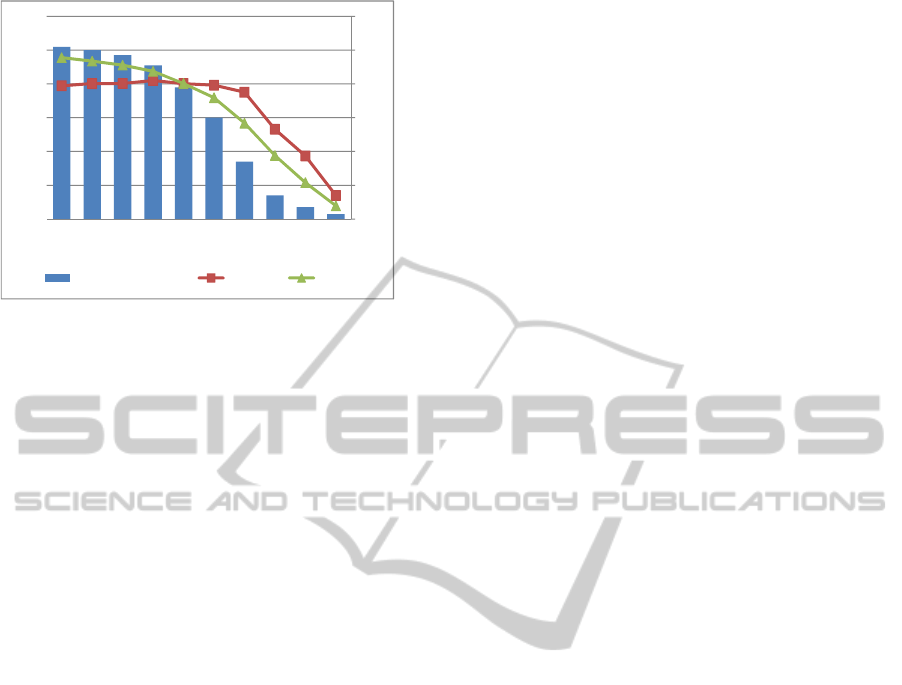
the number of query

Proposal Google

1.0≧ 102 0.394153 0.477867

0.9≧ 100 0.400983 0.467425

0.8≧ 97 0.401148 0.45557

0.7≧ 91 0.410052 0.437263

0.6≧ 78 0.400914 0.401373

0.5≧ 60 0.396087 0.35919

0.4≧ 34 0.37525 0.283838

0.3≧ 14 0.265936 0.18804

0.2≧ 7 0.186868 0.107945

0.1≧ 3 0.069683 0.039227

102

100

0.1

0.2

0.3

0.4

0.5

0.6

100

120

1.0≧ 0.9≧ 0.8≧ 0.7≧ 0.6≧ 0.5≧ 0.4≧ 0.3≧ 0.2≧ 0.1≧

the number of query

Proposal

Google

Figure 1: Reranking results.

which Google returns poor results. Each MAP value

of the point that AP is less than 1.0 represents the ac-

curacy of each method when using all queries.

The point where our method exceeds Google’s AP

is less than 0.6. This means our method is fairly ef-

fective when Google’s result is not good.

5 CONCLUSIONS

We have shown that search results can be improved

by reranking them with various methods based on

Wikipedia features. Experimental results so far in-

dicate the following.

• Category expansion methods are more effective

than a method using a set of categories to which a

query originally belongs.

• Reranking results are improved by deeply related

words but not the number of related words.

• Basically simpler methods work better. However,

more sophisticated methods, that are based on lo-

cal weights of outlinks and inlinks, and global

weights of link co-occurrence and category, work

signiﬁcantly well.

• Any Wikipedia feature works fairly well to im-

prove search results.

Moreover, it turned out that outlinks are much bet-

ter than inlinks to be used for weighting in our meth-

ods. This is interestingly quite contrary to the results

by Chernov et al. When extracting statistical informa-

tion from Wikipedia, we need to carefully choose an

effective model. For this, we think a machine learn-

ing technique like Sumida et al. (Sumida et al., 2008)

would be promising.

In the future research, we are going to extract

more useful data by using Wikipedia features and

classify data using the machine learning.

ACKNOWLEDGEMENTS

This work was supported by JSPS KAKENHI

(21500102).

REFERENCES

Chernov, S., Iofciu, T., Nejdl, W., and Zhou, X. (2006).

Extracting semantic relationships between wikipedia

categories. In Proc. of Workshop on Semantic Wikis

(SemWiki 2006). Citeseer.

Cilibrasi, R. et al. (2007). The google similarity distance.

IEEE Transactions on knowledge and data engineer-

ing, pages 370–383.

Finkelstein, L., Gabrilovich, E., Matias, Y., Rivlin, E.,

Solan, Z., Wolfman, G., and Ruppin., E. (2002).

WordSimilarity-353 Test Collection.

Gabrilovich, E. and Markovitch, S. (2007). Computing se-

mantic relatedness using wikipedia-based explicit se-

mantic analysis. In Proc. of IJCAI-07, pages 6–12.

Hori, K., Oishi, T., Mine, T., Hasegawa, R., Fujita, H.,

and Koshimura., M. (2010). Related Word Extrac-

tion from Wikipedia for Web Retrieval Assistance. In

Proc. of ICAART 2010 vol.2, pages 192–199.

Ito, M., Nakayama, K., Hara, T., and Nishio, S. (2008).

Association thesaurus construction methods based on

link co-occurrence analysis for wikipedia. In Proc. of

the 17th ACM conference on Information and knowl-

edge management, pages 817–826. ACM.

Nakatani, M., Jatowt, A., Ohshima, H., and Tanaka,

K. (2009). Quality evaluation of search results

by typicality and speciality of terms extracted from

wikipedia. In Database Systems for Advanced Appli-

cations, pages 570–584. Springer Berlin/Heidelberg.

Nakayama, K., Hara, T., and Nishio, S. (2007). Wikipedia

mining for an association web thesaurus construction.

Web Information Systems Engineering–WISE 2007,

pages 322–334.

Page, L., Brin, S., Motwani, R., and Winograd, T. (1998).

The pagerank citation ranking: Bringing order to the

web.

Ponzetto, S. and Strube, M. (2006). Wikirelate! computing

semantic relatedness using wikipedia. In Proc. AAAI-

06, pages 1419–1424.

Schutze, H. and Pedersen, J. (1997). A cooccurrence-

based thesaurus and two applications to information

retrieval. Information Processing & Management,

33(3):307–318.

Sumida, A., Yoshinaga, N., and Torisawa, K. (2008). Boost-

ing precision and recall of hyponymy relation acqui-

sition from hierarchical layouts in wikipedia. In Proc.

of the LREC 2008.

Witten, I. and Milne, D.(2008). An effective, low-cost mea-

sure of semantic relatedness obtained from Wikipedia

links. In Proc. of AAAI Workshop on Wikipedia and

Artiﬁcial Intelligence: an Evolving Synergy, AAAI

Press, Chicago, USA, pages 25–30.

EVALUATING RERANKING METHODS USING WIKIPEDIA FEATURES

381