
AN ADAPTIVE SELECTIVE ENSEMBLE FOR DATA STREAMS
CLASSIFICATION
Valerio Grossi
Department of Pure and Applied Mathematics, University of Padova, via Trieste 63, Padova, Italy
Franco Turini
Department of Computer Science, University of Pisa, largo B. Pontecorvo 3, Pisa, Italy
Keywords:
Data Mining, Data Streams Classification, Ensemble Classifier, Concept Drifting.
Abstract:
The large diffusion of different technologies related to web applications, sensor networks and ubiquitous
computing, has introduced new important challenges for the data mining community. The rising phenomenon
of data streams introduces several requirements and constraints for a mining system. This paper analyses a
set of requirements related to the data streams environment, and proposes a new adaptive method for data
streams classification. The outlined system employs data aggregation techniques that, coupled with a selective
ensemble approach, perform the classification task. The selective ensemble is managed with an adaptive
behavior that dynamically updates the threshold value for enabling the classifiers. The system is explicitly
conceived to satisfy these requirements even in the presence of concept drifting.
1 INTRODUCTION
The rapid diffusion of brand new technologies, such
as smartphones, netbooks, sensor networks, related
to communication services, web and safety applica-
tions, has introduced new challenges in data manage-
ment and mining. In these scenarios data arrives on-
line, at a time-varying rate creating the so-called data
stream phenomenon. Conventional knowledge dis-
covery tools cannot manage this overwhelming vol-
ume of data. The nature of data streams requires the
use of new approaches, which involve at most one
pass over the data, and try to keep track of time-
evolving features, known as concept drifting.
Ensemble approaches are a popular solution for
data streams classification (Bifet et al., 2009). In these
methods, classification takes advantage of multiple
classifiers, extracting new models from scratch and
deleting the out-of-date ones continuously. In (Grossi
and Turini, 2010; Grossi, 2009), it was stressed that
the number of classifiers actually involved in the clas-
sification task cannot be constant through time. In the
cited works, it was demonstrated that a selective en-
semble which, based on current data distribution, dy-
namically calibrates the set of classifiers to use, pro-
vides a better performance than systems using a fixed
set of classifiers constant through time. In our for-
mer approach, the selection of the models involved in
the classification step was chosen by a fixed activa-
tion threshold. This choice is the right solution if it
is possible to study a-priori what is the best value to
assign to the threshold. Unfortunately, in many situa-
tions, this information is unavailable, since the stream
data behaviour cannot be modeled. In several real do-
mains, such as intrusion detection, data distribution
can remain stable for a long time, changing radically
when an attack occurs.
This work presents an evolution of the system out-
lined in (Grossi and Turini, 2010; Grossi, 2009). The
new approach introduces a complete adaptive behav-
iuor in the management of the threshold required for
the selection of the set of models actually involved
in the classification. The main contribution of this
work is to introduce an adaptive approach for varying
the value of the model activation threshold through
time, influencing the overall behaviour of the ensem-
ble classifier, based on data change reaction. Our ap-
proach is explicitly explained with the use of binary
attributes. This choice can be seen as a limitation, but
it is worth observing that every nominal attribute can
be easily transformed into a set of binary ones. The
only inability is the direct treatment of numerical val-
136
Grossi V. and Turini F..
AN ADAPTIVE SELECTIVE ENSEMBLE FOR DATA STREAMS CLASSIFICATION.
DOI: 10.5220/0003183501360145
In Proceedings of the 3rd International Conference on Agents and Artificial Intelligence (ICAART-2011), pages 136-145
ISBN: 978-989-8425-40-9
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

ues. Fortunately, (Gama and Pinto, 2006) represents
a general approach to solve the online discretization
of numerical attributes. The proposed method is par-
ticularly suitable in our context, since it proposes a
discretization method based on two layers. The first
layer summarizes data, while the second one con-
structs the final binning. The process of updating the
first layer works online and requires a single scan over
the data.
Paper Organization: Section 2 introduces our refer-
ence scenario. It outlines some requirements that a
system working on streaming environments should
satisfy. Section 3 describes our approach in details,
highlighting how the requirements introduced in Sec-
tion 2.1 are verified by the proposed model. Further-
more, it present how our adaptive selection is imple-
mented. In Section 4, we present a comparative study
to understand how the new adaptive approach guaran-
tees a higher reliability of the system. In this section,
our approach is also compared with other well-know
approaches available in the literature. Finally, Section
5 draws the conclusions and introduces some future
works.
2 DATA STREAMS
CLASSIFICATION
Data streams represent a new challenge for the data
mining community. In a stream scenario, traditional
mining methods are further constrained by the unpre-
dictable behaviour of a large volume of data. The
latter arrives on-line at variable rates, and once an
element has been processed, it must be discarded or
archived. In either cases, it cannot be easily retrieved.
Mining systems have no control over data generation,
and they must be capable of guaranteeing a near real-
time response.
Definition 1. A data stream is an infinite set of el-
ements X = X
1
,...,X
j
,... where each X
i
∈ X has
a + 1 dimensions, (x
1
i
,...x
a
i
,y), and where y ∈ {⊥
,1,... ,C}, and 1,. . . ,C identify the possible values in
a class.
A stream can be divided into two sets based on
the availability of class label y. If value y is available
in the record (y 6=⊥), it belongs to the training set.
Otherwise the record represents an element to clas-
sify, and the true label will only be available after an
unpredictable period of time.
Given Definition 1, the notion of concept drift-
ing can be easily defined. As reported in (Klinken-
berg, 2004), a data stream can be divided into batches,
namely b
1
,b
2
,...,b
n
. For each batch b
i
, data is in-
dependently distributed w.r.t. a distribution P
i
(). De-
pending on the amount and type of concept drifting,
P
i
() will differ from P
i+1
(). A typical example is
customers’ buying preferences, which can change ac-
cording to the day of the week, inflation rate and/or
availability of alternatives. Two main types of con-
cept drifting are usually distinguished in the literature,
i.e. abrupt and gradual. Abrupt changes imply a rad-
ical variation of data distribution from a given point
in time, while gradual changes are characterized by a
constant variation during a period of time. The con-
cept drifting phenomenon involves data expiration di-
rectly, and forces stream mining systems to be con-
tinuously updated to keep track of changes. This im-
plies making time-critical decisions for huge volumes
of high-speed streaming data.
2.1 Requirements
As introduced in Section 2, the stream features influ-
ence the development of a data streams classifier rad-
ically. A set of requirements must be taken into ac-
count before proposing a new approach. These needs
highlightseveral implementationdecisions inserted in
our approach.
Since data streams can be potentially unbounded
in size, and data arrives at unpredictable rates, there
are rigid constraints on time and memory required by
a system through time:
Req. 1: the time required for processing every sin-
gle stream element must be constant, which im-
plies that every data sample can be analyzed al-
most only once.
Req. 2: the memory needed to store all the statistics
required by the system must be constant in time,
and it cannot be related to the number of elements
analyzed by the system.
Req. 3: the system must be capable of updating their
structures readily, working within a limited time
span, and guaranteeing an acceptable level of re-
liability.
Given Definition 1, it is clear that the elements to clas-
sify can arrive in every moment during the data flow.
Req. 4: the system must be able to classify unseen
elements every time during its computation.
Req. 5: the system should be able to manage a set of
models that do not necessarily include contiguous
ones, i.e. classifiers extracted using adjacent parts
of the stream.
AN ADAPTIVE SELECTIVE ENSEMBLE FOR DATA STREAMS CLASSIFICATION
137

2.2 Related Work
Mining data streams has rapidly become an important
and challenging research field. As proposed in (Gaber
et al., 2005), the available solutions can be classi-
fied into data-based and task-based ones. In the for-
mer approaches a data stream is transformed into an
approximate smaller-size representation, while task-
based techniques employ methods from computa-
tional theory to achieve time and space efficient solu-
tions. Aggregation (Aggarwal et al., 2003; Aggarwal
et al., 2004a; Aggarwal et al., 2004b; Lin and Zhang,
2008), sampling (Domingos and Hulten, 2001) or
summarized data structure, such as histograms (Guha
et al., 2001; Gilbert et al., 2002), are popular example
of data-based solutions. On the contrary, approxima-
tion algorithms approaches such as those introduced
in (Gama et al., 2006; Domingos and Hulten, 2001)
are examples of task-based techniques.
In the context of data streams classification, two
main approaches can be outlined, namely instance se-
lection and ensemble learning. Very Fast Decision
Trees (VFDT) (Domingos and Hulten, 2000) with its
improvements (Hulten et al., 2001; Gama and Pinto,
2006; Pfahringer et al., 2008) for concept drifting re-
action and numerical attributes managing represent
examples of instance selection methods. In particular,
the Hoeffding bound guarantees that the split attribute
chosen using n examples, is the same with high proba-
bility as the one that would be chosen using an infinite
set of examples. Last et al. (Cohen et al., 2008) pro-
pose another strategy using an info-fuzzy technique to
adjust the size of a data window. Ensemble learning
employs multiple classifiers, extracting new models
from scratch and deleting the out-of-date ones con-
tinuously. Online approaches for bagging and boost-
ing are available in (Oza and Russell, 2001; Chu and
Zaniolo, 2004; Bifet et al., 2009). Different methods
are available in (Street and Kim, 2001; Wang et al.,
2003; Scholz and Klinkenberg, 2005; Kolter and Mal-
oof, 2007; Folino et al., 2007), where an ensemble
of weighted-classifiers, including an adaptive genetic
programming boosting, as in (Folino et al., 2007), is
employed to cope with concept drifting. None of the
two techniques can be assumed to be more appro-
priate than the other. (Bifet et al., 2009) provides a
comparison between different techniques not only in
terms of accuracy, but also including computational
features, such as memory and time required by each
system. By contrast, our approach proposes an en-
semble learning that differs from the cited methods
since it is designed to concurrently manage different
sliding windows, enabling the use of a set of classi-
fiers not necessarily contiguous and constant in time.
x y z
class value
0 1 1
no
0 1 0
yes
0 1 1
no
1 1 1
yes
1 0 0
yes
1 0 1
no
1 1 1
yes
0 0 0
ind
0 0 1
yes
0 0 0
ind
(a) A stream chunk of 10 ele-
ments
S
10
=
(
x
,2,3) (
y
,2,3) (
z
,3,2)
yes
(
x
,2,1) (
y
,2,1) (
z
,0,3)
no
(
x
,2,0) (
y
,2,0) (
z
,2,0)
ind
(b) The resulting snapshot
Figure 1: From data stream (a) to snapshot (b).
3 ADAPTIVE SELECTIVE
ENSEMBLE
A detailed description of our system is available in
(Grossi and Turini, 2010; Grossi, 2009). In the
following subsections, we briefly introduce only the
main concepts of our approach highlighting the re-
lations between the requirements outlined in Section
2.1 and the aggregate structures introduced. The pro-
posed structures are primarily conceived to capture
evolving data features, and guarantee data reduction
at the same time. Unfortunately, ensuring a good
trade-off between data reduction, and a powerful rep-
resentation of all the evolving data factors is a non-
trivial task.
3.1 The Snapshot
The snapshot definition implies the na¨ıve Bayes clas-
sifier directly. In our model, the streaming training
set is partitioned into chunks. Each data chunk is
transformed into an approximate more compact form,
called snapshot.
Definition 2 (Snapshot). Given a data chunk of k el-
ements, with A attributes and C class values, a snap-
shot computes the distribution of the values of at-
tribute a ∈ A with class value c, considering the last k
elements arrived:
S
k
:C × A 7→ freq
a,k, c
, ∀a ∈ A,c ∈ C
The following properties are directly derived from
Definition 2.
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
138

Property 1. Given a stream with C class values and
A attributes, a snapshot is a set of C × A tuples.
Property 2. Building a snapshot S
k
requires k ac-
cesses to the data stream. Every element is accessed
only once. Computing a snapshot is linear to the k
number of elements.
Figure 1 shows an example of snapshot creation. The
latter implies only a single access to every stream ele-
ment. A snapshot is built incrementally accessing the
data one by one, and updating the respective counters.
Properties 1 and 2 guarantee that a snapshot requires
a constant time and memory space, satisfying require-
ments 1 and 2.
3.1.1 Snapshots of Higher Order
The only concept of snapshot is not sufficient to guar-
antee all the features needed for data managing and
drift reaction. The concept of high-order snapshot is
necessary to maximize data availability for the mining
task guaranteeing only one data access.
Definition 3 (High-Order snapshot). Given an order
value i > 0, a high-order snapshot, is obtained by
summing h snapshots of i− 1 order:
S
i
h×k
=
h
∑
j=1
S
i−1
k, j
h
∑
j=1
freq
j
a,k, c
i−1
, ∀a ∈ A,c ∈ C
where, given a class value c and an attribute a,
freq
j
a,k, c
i−1
refers to the distribution of the val-
ues of attribute a with class value c of the j-th snap-
shot of order i− 1.
Figure 2 shows the relation between snapshots and
their order. The aim is to employ a set of snapshots
created directly from the stream to build new ones,
representingincreasingly larger data windows,simply
by summing the frequencies of their elements.
A high-order snapshot satisfies Property 1, since
it has the same structure of a basic one. Moreover,
it further verifies requirements 3, since the creation
of a new high-order snapshot is linear in the number
of attributes and class values. Finally, the creation of
high-order snapshots does not imply any loss of in-
formation. This aspect guarantees that a set of differ-
ent size sliding windows can be simultaneously man-
aged by accessing data stream only once, enabling the
approach to consider every window as computed di-
rectly from the stream.
From a snapshot, or a high-order one, the system
extracts an approximated decision tree, or employs
the snapshot as na¨ıve Bayes classifier directly.
3.2 The Frame
Snapshots are stored to maximize the number of el-
ements for training classifiers. A model mined from
a small set of elements tends to be less accurate than
the one extracted from a large data set. If this ob-
servation is obvious in “traditional” mining contexts,
where training sets are accurately built to maximize
the model reliability, in a stream environment this is
not necessarily true. Due to concept drifting, a model
extracted from a large set of data can be less accu-
rate than the one mined from a small training set.
The large data set can include mainly out-of-date con-
cepts.
Snapshots are then stored and managed, based on
their order, in a structure called frame. The order of a
snapshot defines its level of time granularity. Concep-
tually similar to Pyramidal Time Frame introduced by
Aggarwal et al. in (Aggarwal et al., 2003) and inher-
ited by logarithmic tilted-time window, our structure
sorts snapshots based on the number of elements from
which a snapshot was created.
Definition 4 (Frame). Given a level value i, and a
level capacity j, a frame is a function that, given a
pair of indexes (x,y) returns a snapshot of order x and
position y:
F
i, j
: (x, y) 7→ Snapshot
x,y
where: x ∈ {0,...,i− 1} and y ∈ {0,..., j − 1}.
As shown in Figure 3, level 1 contains snapshots
created directly from the stream. Upper levels use the
snapshots of the layer immediately lower to create a
new one. The maximum number of snapshots avail-
able in the frame is constant in time and is defined
by the number of levels and the level capacity. For
each layer, the snapshot are stored with FIFO policy.
The frame memory occupation is constant in time and
is linear with the number of snapshots storable in the
structure.
3.3 Ensemble Management
The concepts introduced in Section 3.1 and 3.2 are
employed to define and manage an ensemble of clas-
sifiers. The selective ensemble management can be
briefly described as a four phase approach:
1. For each snapshot S
j
i
, a triple (C
i
,w
i
,b
i
) represent-
ing the classifier, its weight and the classifier en-
abling variable b
i
is extracted from S
j
i
.
2. Since data distribution can change through time,
the models currently in the structure are re-
weighed with the new data distribution, using a
test set of complete data taken from the last por-
tion of the stream directly.
AN ADAPTIVE SELECTIVE ENSEMBLE FOR DATA STREAMS CLASSIFICATION
139

e
i,1
,. . .,e
i,k
| {z }
S
k, j
e
i+1,1
,. . .,e
i+1,k
| {z }
S
k, j+1
| {z }
S
2
2k, j
e
i+2,1
,. . .,e
j+2,k
| {z }
S
k, j+2
e
i+3,1
,. . .,e
i+3,k
| {z }
S
k, j+3
| {z }
S
2
2k, j+1
| {z }
S
3
4k, j
.. . e
n,1
,. . .,e
n,k
| {z }
S
k,n
e
n+1,1
,. . .,e
n+1,k
| {z }
S
k,n+1
.. .
Figure 2: Snapshots and their order.
level
1
S
k, j+2
S
k, j+1
S
k, j
2
S
2
2k,l+2
S
2
2k,l+1
S
2
2k,l
3
S
3
4k,g+2
S
3
4k,g+1
S
3
4k,g
4
...
...
i S
i
2
i−1
k,n+2
S
i
2
i−1
k,n+1
S
i
2
i−1
k,n
Figure 3: The frame structure.
3. Given a level i, every time a new classifier is gen-
erated, the system decides if the new model must
be inserted in the ensemble based on new data dis-
tribution. Apart from the lowest level, where the
new one is inserted in any case, the system selects
the k
i
most promising models, based on the cur-
rent weight associated to the classifiers, to clas-
sify the new data distribution from k
i
+ 1 models
correctly.
4. Finally, a set of active models is selected, setting
the boolean value b
i
associated with a C
i
as true.
The set of active models is selected based on the
value of an activation threshold θ. All the classi-
fiers that differ at most θ to the best classifier with
the highest weight are enabled.
The defined approach satisfies requirements 4 and 5,
since it can classify a new instance every time it is
required, and can employ a set of not necessarily con-
tiguous classifiers, since it is not necessarily true that
every classifier generated through time enters the en-
semble, but even in that case it can be disabled.
Figure 4 shows the overall organization of our ap-
proach. Essentially, for each level in the frame struc-
ture we have a corresponding level in the ensemble.
The subdivision of the data aggregation task from the
mining aspects makes our approach suitable in dis-
tributed/parallel environments as well. One or more
components can be employed to manage the concepts
of snapshot and frame, while another can manage the
ensemble classifier.
3.4 Adaptive Behaviour
As proposed in Section 3.3 our approach has two key
factors influencing its behavior, the weight measure
to employ and the selection of the θ value. If in the
literature, several weight measures, mainly related to
classifier accuracy, are available and guarantee a good
reliability of the system, the θ threshold represents the
real key factor for the quality of our approach.
In our experiments (Grossi, 2009), we noticed that
the reliability of the system is heavily influenced by
the θ value. As we shall present in Section 4.3, in-
dependently from the data set employed, activation
values which are too high (or too small) decrease the
predictive power of the ensemble. On the one hand, in
case of relatively stable data, small activation thresh-
old values limit the use of a large set of classifiers.
On the contrary, large threshold values damage the se-
lective ensemble in the case of concept drifts. In the
cited experiments, the θ value was fixed by the user
and it did not change through time. Only our experi-
ence and the experimental results drove the selection
of the right value.
The main contribution of this work is to introduce
an adaptive approach into our system. In particular,
we introduce a new approach for varying the value of
the activation threshold through time, thus influencing
the overall behaviour of the entire system, based on
data change reaction.
The basic idea of the adaptive approach is similar
to the additive-increase/multiplicative-decrease algo-
rithm adopted by TCP Internet protocol for managing
the transfer rate value used in TCP congestion avoid-
ance.
The pseudo-code of the method for managing the
activation threshold is proposed in Figure 5. The
idea behind the algorithm is quite simple. When the
first model is inserted in the structure, the activation
threshold and the number of active models are ini-
tialized (Steps 1-5). Successively, every time a new
model is inserted in the ensemble, the procedure at
Step 6 computes how many models will be activated
with the current θ value. If the number of models po-
tentially activatable is higher than the old one (Step
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
140
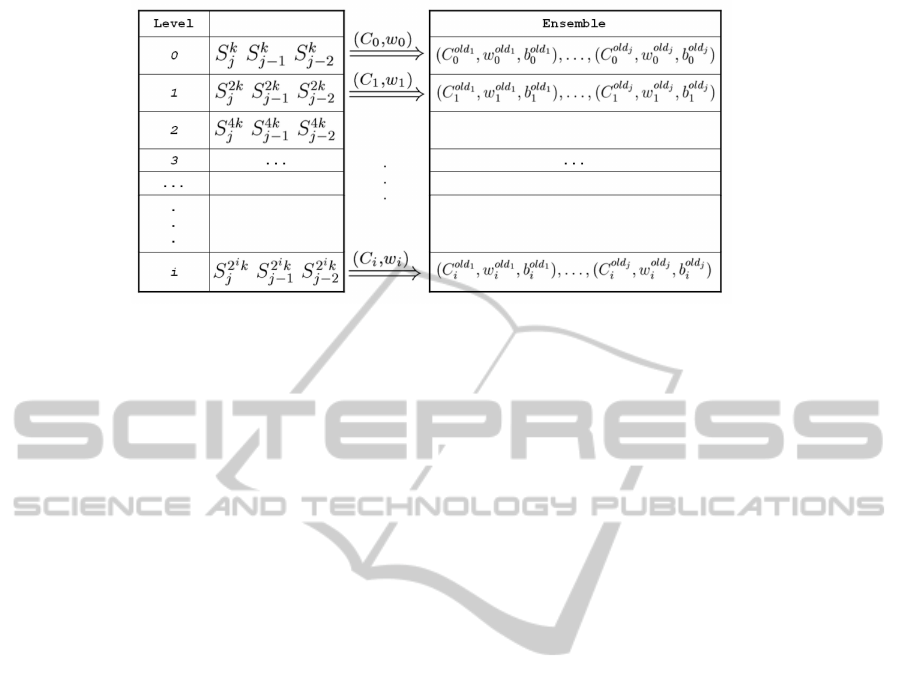
Figure 4: The overall system architecture.
Activation Threshold Algorithm
1: if (oneModel() = true) then
2: θ ← 0.00; activation threshold initialized
3:
oldActModels
← 1
4: return
5: end if
6:
actModels
← getActiveModel(θ)
7: if (
actModels
>
oldActModels
) then
8: θ ← θ + 0.01; increment threshold value
9: else if (
actModels
<
oldActModels
) then
10: θ ← θ div 2; decrement threshold value
11: end if
12:
oldActModels
← actModels
13: return
Figure 5: Pseudo-code of the activation threshold algo-
rithm.
7), the threshold is increased. This situation can hap-
pen, when the data distribution remains stable and the
new inserted model is immediately enabled (Step 7-
8). Increasing the threshold value, we can obtain a
better exploitation of the ensemble. On the contrary,
if the number of active models decreases from the pre-
vious invocation, the threshold has to be decreased.
It is useless and dangerous to maintain the current
value, since a data change might be in progress (Step
9-10). It is worth observing that, if the number of
models does not change between the two invocations,
the threshold does not change, since there is no evi-
dence of model improving or data change.
From a computational point of view the algorithm
does not introduce appreciable overhead. Only the
getActiveModel() procedure requires to access the en-
semble structure. If we consider n as the number of
classifiers storable in the ensemble, the complexity of
the algorithm is linear in O(n).
The experimental section demonstrates that our
system is no more heavilyinfluenced by θ value, since
it changes automatically, adapting it to data distribu-
tion.
4 COMPARATIVE
EXPERIMENTAL EVALUATION
4.1 Data Sets
Several synthetic data sets were introduced in our ex-
periments. This kind of data enables an exhaustive in-
vestigation about the reliability of the stream systems
involving different scenarios. The data behaviour can
be described exactly, characterizing the number of
concept drifts, the rate between a change to another
and the number of irrelevant attributes, or the percent-
age of noisy data.
LED24: Proposed by Breiman et al. in (Breiman
et al., 1984), this generator creates data for a display
with 7 LEDs. In addition to the 7 necessary attributes,
17 irrelevant boolean attributes with random values
are added, and 10 percent of noise is introduced, to
make the solution of the problem harder. This type of
data generates only stable data sets.
Stagger: Introduced by Schlimmer and Granger
in (Schlimmer and Granger, 1986), this prob-
lem consists of three attributes, namely
colour
∈
{green, blue, red},
shape
∈ {triangle, circle,
rectangle}, and
size
∈ {small, medium, large},
and a class
y
∈ {0, 1}. In its original formulation,
the training set includes 120 instances and consists
of three target concepts occurring every 40 instances.
The first set of data is labeled according to the con-
cept
color
= red ∧
size
= small, while the others
include
color
= green ∨
shape
= circle and
size
= medium ∨
size
= large. For each training in-
stance, a test set of 100 elements is randomly gener-
ated according to the current concept.
cHyper: Introduced in (Chu and Zaniolo, 2004),
geometrically, a data set is generated by using a
n-dimensional unit hypercube, and an example x is a
AN ADAPTIVE SELECTIVE ENSEMBLE FOR DATA STREAMS CLASSIFICATION
141

vector of n-dimensions x
i
∈ [0,1]. The class boundary
is a hyper-sphere of radius r and center c. Concept
drifting is simulated by changing the c position by a
value ∆ in a random direction. This data set generator
introduces noise by randomly flipping the label of a
tuple with a given probability. Two additional data
sets, namely
Hyper
and
Cyclic
are generated using
this approach.
Hyper
does not consider any drifts,
while
Cyclic
proposes the problem of periodic
recurring concepts.
The features of the data sets actually employed are
reported in Table 1. The stable
LED24
and
Hyper
are
useful for testing whether the mechanism for change
reaction has implications for the reliability of the sys-
tems. The evolving data sets test different features of
a stream classification system. The
Stagger
problem
verifies, if all the systems can cope with concept drift-
ing, without considering any problem dimensionality.
Then, the problem of learning in the presence of con-
cept drifting is evaluated with the other data sets, also
considering a huge quantity of data with
cHyper
.
4.2 Systems
Different popular stream ensemble methods are intro-
duced in our experiments. All the systems expect the
data streams to be divided into chunks based on a de-
fined value. All the approaches are implemented in
Java 1.6 with MOA (The University of Waikato, a)
and WEKA libraries (The University of Waikato, b)
for the implementation of the basic learners and em-
ploy complete non-approximate data for the mining
task.
Fix: This approach is the simplest one. It considers
a fixed set of classifiers, managed as a FIFO queue.
Every classifier is unconditionally inserted in the en-
semble, removing the oldest one, when the ensemble
is full.
SEA: A complete description and evaluation of this
system can be found in (Street and Kim, 2001). In this
case classifiers are not deleted indiscriminately. Their
management is based on a weight measure related to
model reliability. This method represents a special
case of our selective ensemble, where only one level
is defined.
DWM: This system is introduced in (Kolter and Mal-
oof, 2005; Kolter and Maloof, 2007). The approach
implemented here considers a set of data as input to
the algorithm, and a batch classifier as the basic one.
A weight management is introduced, but differently
from SEA, every classifier has a weight associated
with it, when it is created. Every time the classifier
makes a mistake, its weight decreases.
Oza: This system implements the online bagging
method of Oza and Russell (Oza and Russell, 2001)
with the addition of the
ADWIN
technique (Bifet et al.,
2009) as a change detector and as estimator of the
weight of the boosting method.
Single: This approach employs an incremental single
model with EDDM (Gama et al., 2004; Baena-Garcia
et al., 2006) techniques for drift detection. Both Oza
and Single were tested using ASHoeffdingTree and
na¨ıve Bayes models available in MOA.
4.3 Results
All the experiments were run on a PC with In-
tel E8200 DualCore with 4Gb of RAM, employing
Linux Fedora 10 (kernel 2.6.27) as operating system.
Our experiments consider a frame with 8 levels of ca-
pacity 3. Every high-order snapshot is built by adding
2 snapshots. This frame size is large enough to con-
sider snapshots that represent big portions of data at
higher-levels. For each level, an ensemble of 8 classi-
fiers was used. The tests were conducted comparing
the use of the na¨ıve Bayes (NB), and the decision tree
(DT) as base classifiers. In all the cases, we compare
our Selective Ensemble (SE) (with fixed model acti-
vation threshold set to 0.1 and 0.25) with our Adap-
tive Selection Ensemble ASE. For each data genera-
tor, a collection of 100 training sets (and correspond-
ing test sets) are randomly generated with respect to
the features outlined in Table 1. Every system is run,
and the average accuracy and 95% of interval confi-
dence are reported. Each test consists of a set of 100
observations. All the statistics reported are computed
according to the results obtained.
4.3.1 Results with Stable Data Sets
The results obtained with stable data sets confirm that
the drift detection approach provided by each system
does not heavily influence its overall accuracy. With
LED24
and
Hyper
problems, all the systems reach a
quite accurate result. Table 2 reports the results ob-
tained with
Hyper
data sets using the na¨ıve Bayes
approach. These results can be compared with the
ones provided in Table 3 in Section 4.3.1, where the
concept drifting problem is added to the same type of
data.
It is worth observing that there are no significant
differences between the results obtained by SE ap-
proach, varying the model activation threshold, and
the new ASE approach provides a result in line with
the best ones. These results demonstrate that the
adaptive behavior mechanism does not negatively in-
fluence the reliability of the system in the case of sta-
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
142

Table 1: Description of data sets.
dataSet #inst #attrs #irrAttrs #classes %noise #drifts
LED24
a/b/test
10k / 100k / 25k 24 17 10 10% none
Hyper
a/b/test
10k / 100k / 25k 15 0 2 0 none
Stagger
a/test
1200 / 120k 9 0 2 0 3 (every 400) / (every 40k)
Stagger
b/test
12k / 1200k 9 0 2 0 3 (every 4k) / (every 400k)
cHyper
a/b/c
10k / 100k / 1000k 15 0 2 10% 20 (every 500) / (every 5k) / (every 50k)
cHyper
test
250k 15 0 2 10% 20 (every 12.5k)
Cyclic
600k 25 0 2 5% 15×4 (every 10k)
Cyclic
test
150k 25 0 2 5% 15×4 (every 2.5k)
Table 2: Results using na¨ıve Bayes with the
Hyper
problem.
Hyper
a
/
Hyper
b
avg std dev conf
ASE 92.74 / 93.93 1.92 / 2.88 0.38 / 0.49
SE
0.1
92.72 / 93.92 2.20 / 2.52 0.43 / 0.50
SE
0.25
92.70 / 93.91 2.22 / 2.53 0.43 / 0.50
Fix
64
91.82 / 92.35 2.54 / 2.98 0.50 / 0.58
SEA
64
92.97 / 94.44 1.80 / 1.64 0.50 / 0.32
DWM
64
91.82 / 92.76 2.12 / 2.74 0.42 / 0.54
Oza
64
92.39 / 93.73 2.30 / 0.40 0.45 / 0.08
Single 90.04 / 92.68 3.25 / 2.82 0.64 / 0.55
ble data streams. On the contrary, the new approach
enables a better ensemble exploitation.
Moreover, Table 2 highlights that Single model
requires a large quantity of data to provide a good
performance. Finally, Fix
64
and SEA
64
provide good
results that, compared with the ones obtained by
the same systems analyzing the
cHyper
and
Cyclic
problems, demonstrate that these kinds of approaches
guarantee appreciable results only with a quite sta-
ble phenomenon. They do not provide a fast reaction
to concept drifting, since the models involved in the
classification task are constant in time, and when a
drift occurs, they have to change a large part of the
models, before classifying new concepts correctly.
4.3.2 Results with Evolving Data Sets
Table 3 reports the overall results obtained analyz-
ing the
cHyper
problem, considering both decision
tree and na¨ıve Bayes models. Differently from the
results obtained with stable data sets, it is worth ob-
serving that the active model threshold influences the
overall results. Varying the value from 0.1 to 0.25,
and especially considering
cHyper
a
and
cHyper
b
, SE
system presents a difference even larger than 6% be-
tween the two values. On the contrary, our ASE
approach provides an accuracy in line with the best
value, even considering standard deviation. This de-
mostrates that, without knowing the ideal threshold
value for model activation, our ASE approach rep-
resents the right solution to the different situations
involved in a stream scenario, and simulated by the
three cases of the
cHyper
problem. As stated in the
previous section, it is worth observing the poor perfor-
mances of Fix and SEA in the case of evolving data.
These obsevations are further validated by the results
obtained with the
Stagger
problem, that essentially
follow the ones proposed in Table 3.
Finally, Table 4 outlines the resources required by
the systems. The memory requirements were tested
using NetBeans 6.8 Profiler. We can state that Single
requires less memory than ensemble methods, which
need a quantity of memory that is essentially linear
with respect to the number of classifiers stored in the
ensemble. The different nature of the two classes
of systems influences this value. The average mem-
ory required by our system is slightly higher than the
others, since our system manages two different struc-
tures, as suggested at the end of Section 3.3. The run
time behavior confirms this trend. In this case the drift
detection approach influences the execution time of
a method. Let us compare the bagging method Oza
with respect to DWM, SEA
64
and ASE. These tests
highlight that incremental single model systems are
faster than ensemble ones, since they have to update
only one model. On the contrary, considering the ac-
curacy, single model systems rarely provide best av-
erage values. Finally, Oza guarantees an appreciable
reliability with every data set, but its execution time
is definitely higher than the others.
We conclude this section, proposing the results
obtained considering the
Cyclic
problem. The latter
are presented considering the na¨ıve Bayes approach
and analyzing different rates between the chunk size
and the elements to classify. As shown in Figure 6,
even in this case, our ASE approach is in-line with
the SE
0.1
and better than the others. Since this prob-
lem presents recurring concepts, it is worth observing
AN ADAPTIVE SELECTIVE ENSEMBLE FOR DATA STREAMS CLASSIFICATION
143
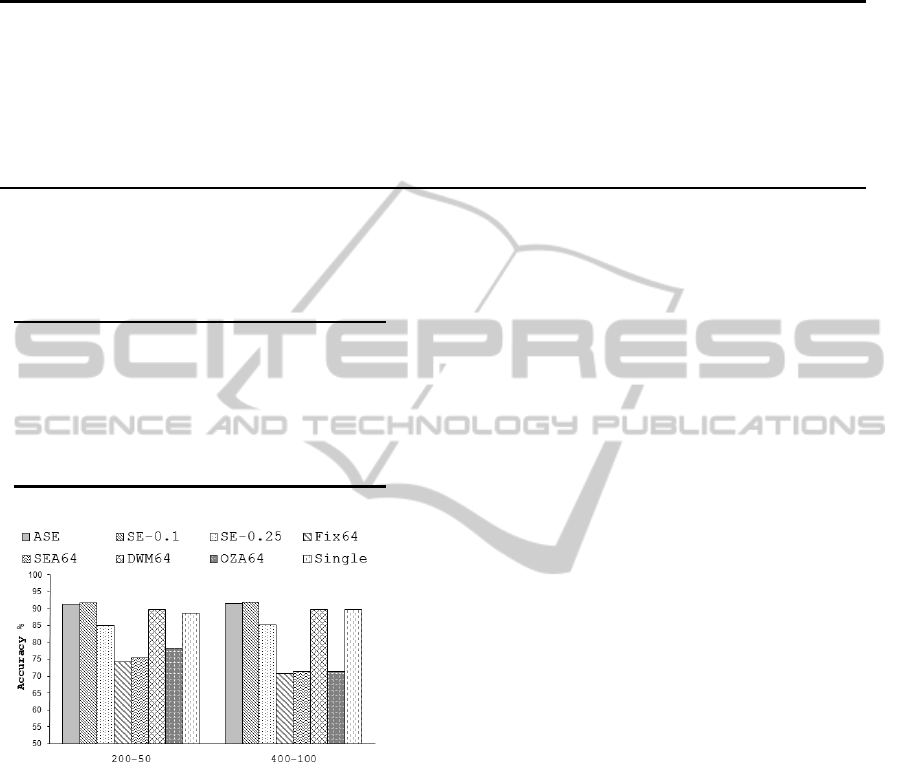
Table 3: Overall results with the
cHyper
problem.
cHyper
a
/
cHyper
b
/
cHyper
c
- decision tree
cHyper
a
/
cHyper
b
/
cHyper
c
- na¨ıve Bayes
avg std dev conf avg std dev conf
ASE 83.58 / 88.72 / 93.19 0.51 / 0.40 / 0.28 0.10 / 0.08 / 0.06 87.52 / 92.23 / 95.94 0.38 / 0.43 / 0.33 0.09 / 0.08 / 0.06
SE
0.1
84,05 / 89,43 / 93,09 0,49 / 0,40 / 0,32 0,10 / 0,08 / 0,06 87,62 / 92,62 / 95,98 0,42 / 0,43 / 0,47 0,08 / 0,09 / 0,09
SE
0.25
78,42 / 86,10 / 91,86 0,86 / 0,35 / 0,23 0,17 / 0,07 / 0,23 79,90 / 86,80 / 92,14 0,83 / 0,40 / 0,22 0,16 / 0,08 / 0,22
Fix
64
70,26 / 82,02 / 90,62 2,58 / 1,23 / 0,13 0,51 / 0,24 / 0,13 73,72 / 83,69 / 94,16 2,60 / 1,35 / 0,40 0,51 / 0,26 / 0,40
SEA
64
70,26 / 82,14 / 90,04 2,58 / 1,10 / 0,14 0,51 / 0,22 / 0,14 73,72 / 84,23 / 94,78 2,60 / 1,27 / 0,31 0,51 / 0,25 / 0,31
DWM
64
77,75 / 85,18 / 92,65 1,94 / 0,60 / 0,14 0,38 / 0,04 / 0,14 85,93 / 92,18 / 95,63 1,76 / 0,18 / 0,38 0,35 / 0,04 / 0,38
Oza
64
81,99 / 89,60 / 92,40 0,97 / 0,37 / 0,25 0,19 / 0,07 / 0,25 80,01 / 87,31 / 89,78 1,23 / 0,54 / 0,56 0,24 / 0,11 / 0,56
Single 81,50 / 87,85 / 89,99 1,60 / 0,70 / 0,34 0,31 / 0,14 / 0,34 81,25 / 89,47 / 93,34 2,02 / 0,87 / 0,84 0,40 / 0,17 / 0,84
Table 4:
cHyper
c
time and memory required.
decision tree na¨ıve Bayes
avg used run time avg used run time
heap (KB) (sec.) heap (KB) (sec.)
ASE 9276 82,40 7572 27,42
SE 9233 80,80 7894 27,45
Fix
64
8507 47,54 5317 23,82
SEA
64
7980 152,07 5371 97,76
DWM
64
5111 77,56 5137 21,21
Oza
64
10047 393,93 6664 290,24
Single 5683 11,54 5399 8,26
Figure 6: Average accuracy using na¨ıve Bayes with the
Cyclic
problem.
how our approach can exploit the selective ensemble
better than the others, since some models which are
currently out of context are not deleted by the sys-
tem, but simply disabled. If a concept becomes newly
valid, the model can be reactivated. This behaviour is
still valid, even in the case of the adaptive approach.
5 CONCLUSIONS
The preliminary results show that, with respect to the
use of a fixed threshold, our adaptive algorithm pro-
vides a slightly worst performance than the ones of
the best value of the threshold. Unfortunately, the
choice of the best value is not always feasible, and
if a wrong selection is made, the system loses its pre-
cision. On the contrary, our adaptive approach does
not require any assumption about active model values
and displays good adaptation to the different scenar-
ios. This work represents a first step to guarantee a
system completely adaptable to the different stream-
ing factors. As future works, our aims are to test our
adaptive model in a real stream application with real
data. Moreover, we are currently studying the intro-
duction of runtime monitoring tools for automatically
adapting our system, e.g varying the number of frame
levels, or the models available for each layer, dynam-
ically considering memory consumption and time re-
sponse constraints.
REFERENCES
Aggarwal, C. C., Han, J., Wang, J., and Yu, P. (2003).
A framework for clustering evolving data streams.
In Proceedings of the 2003 International Conference
on Very Large Data Bases (VLDB’03), pages 81–92,
Berlin, Germany.
Aggarwal, C. C., Han, J., Wang, J., and Yu, P. (2004a).
A framework for projected clustering of high dimen-
sional data streams. In Proceedings of the 2004 In-
ternational Conference on Very Large Data Bases
(VLDB’04), pages 852–863, Toronto, Canada.
Aggarwal, C. C., Han, J., Wang, J., and Yu, P. (2004b). On
demand classification of data streams. In Proceedings
of the 10th International Conference on Knowledge
Discovery and Data Mining (KDD’04), pages 503–
508, Seattle, WA.
Baena-Garcia, M., del Campo-Avila, J., Fidalgo, R., Bifet,
A., Ravalda, R., and Morales-Bueno, R. (2006). Early
drift detection method. In International Workshop on
Knowledge Discovery from Data Streams.
Bifet, A., Holmes, G., Pfahringer, B., Kirby, R., and
Gavald´a, R. (2009). New ensemble methods for evolv-
ing data streams. In Proceedings of the 15th Interna-
tional Conference on Knowledge Discovery and Data
Mining, pages 139–148.
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
144

Breiman, L., Friedman, J., Olshen, R., and Stone, C. (1984).
Classification and Regression Trees. Wadsworth Inter-
national Group, Belmont, CA.
Chu, F. and Zaniolo, C. (2004). Fast and light boosting for
adaptive mining of data streams. In Proceedings of the
8th Pacific-Asia Conference Advances in Knowledge
Discovery and Data Mining (PAKDD’04), pages 282–
292, Sydney, Australia.
Cohen, L., Avrahami, G., Last, M., and Kandel, A.
(2008). Info-fuzzy algorithms for mining dynamic
data streams. Applied Soft Computing, 8(4):1283–
1294.
Domingos, P. and Hulten, G. (2000). Mining high-speed
data streams. In Proceedings of the 6th International
Conference on Knowledge Discovery and Data Min-
ing (KDD’00), pages 71–80, Boston. MA.
Domingos, P. and Hulten, G. (2001). A general method
for scaling up machine learning algorithms and its
application to clustering. In Proceedings of the
18th International Conference on Machine Learning
(ICML’01), pages 106–113, Williamstown, MA.
Folino, G., Pizzuti, C., and Spezzano, G. (2007). Mining
distributed evolving data streams using fractal gp en-
sembles. In Proceedings of the 10th European Confer-
ence Genetic Programming (EuroGP’07), pages 160–
169, Valencia, Spain.
Gaber, M. M., Zaslavsky, A., and Krishnaswamy, S. (2005).
Mining data streams: a review. ACM SIGMOD
Records, 34(2):18–26.
Gama, J., Fernandes, R., and Rocha, R. (2006). Decision
trees for mining data streams. Intelligent Data Analy-
sis, 10(1):23–45.
Gama, J., Medas, P., Castillo, G., and Rodrigues, P. (2004).
Learning with drift detection. In SBIA Brazilian Sym-
posium on Artificial Intelligence, pages 286–295.
Gama, J. and Pinto, C. (2006). Discretization from data
streams: applications to histograms and data min-
ing. In Proceedings of the 2006 ACM symposium on
Applied computing (SAC’06), pages 662–667, Dijon,
France.
Gilbert, A., Guha, S., Indyk, P., Kotidis, Y., Muthukrish-
nan, S., and Strauss, M. (2002). Fast, small-space
algorithms for approximate histogram maintenance.
In Proceedings of the 2002 Annual ACM Symposium
on Theory of Computing (STOC’02), pages 389–398,
Montreal, Quebec, Canada.
Grossi, V. (2009). A New Framework for Data Streams
Classification. PhD thesis, Supervisor Prof. Franco
Turini, University of Pisa.
Grossi, V. and Turini, F. (2010). A new selective ensemble
approach for data streams classification. In Proceed-
ings of the 2010 International Conference in Artificial
Intelligence and Applications (AIA’2010), pages 339–
346, Innsbruck, Austria.
Guha, S., Koudas, N., and Shim, K. (2001). Data-
streams and histograms. In Proceedings of the 2001
Annual ACM Symposium on Theory of Computing
(STOC’01), pages 471–475, Heraklion, Crete, Greece.
Hulten, G., Spencer, L., and Domingos, P. (2001). Min-
ing time changing data streams. In Proceedings of the
7th International Conference on Knowledge Discov-
ery and Data Mining (KDD’01), pages 97–106, San
Francisco, CA.
Klinkenberg, R. (2004). Learning drifting concepts: Exam-
ple selection vs. example weighting. Intelligent Data
Analysis, 8:281–300.
Kolter, J. Z. and Maloof, M. A. (2005). Using additive ex-
pert ensembles to cope with concept drift. In Proceed-
ings of the 22nd International Conference on Machine
learning (ICML’05), pages 449–456, Bonn, Germany.
Kolter, J. Z. and Maloof, M. A. (2007). Dynamic weighted
majority: An ensemble method for drifting concepts.
Journal of Machine Learning Research, 8:2755–2790.
Lin, X. and Zhang, Y. (2008). Aggregate computation
over data streams. In Procedings of the 10th Asia
Pacific Web Conference (APWeb’08), pages 10–25,
Shenyang, China.
Oza, N. C. and Russell, S. (2001). Online bagging and
boosting. In Proceedings of 8th International Work-
shop on Artificial Intelligence and Statistics (AIS-
TATS’01), pages 105–112, Key West, FL.
Pfahringer, B., Holmes, G., and Kirkby, R. (2008). Han-
dling numeric attributes in hoeffding trees. In
Proceeding of the 2008 Pacific-Asia Conference on
Knowledge Discovery and Data Mining (PAKDD’08),
pages 296–307, Osaka, Japan.
Schlimmer, J. C. and Granger, R. H. (1986). Beyond in-
cremental processing: Tracking concept drift. In Pro-
ceedings of the 5th National Conference on Artificial
Intelligence, pages 502–507, Menlo Park, CA.
Scholz, M. and Klinkenberg, R. (2005). An ensemble
classifier for drifting concepts. In Proceeding of
2nd International Workshop on Knowledge Discovery
from Data Streams, in conjunction with ECML-PKDD
2005, pages 53–64, Porto, Portugal.
Street, W. N. and Kim, Y. (2001). A streaming ensem-
ble algorithm (SEA) for large-scale classification. In
Proceedings of the 7th International Conference on
Knowledge Discovery and Data Mining (KDD’01),
pages 377–382, San Francisco, CA.
The University of Waikato. MOA: Mas-
sive Online Analysis, August 2009.
http://www.cs.waikato.ac.nz/ml/moa.
The University of Waikato. Weka 3: Data
Mining Software in Java, Version 3.6.
http://www.cs.waikato.ac.nz/ml/weka.
Wang, H., Fan, W., Yu, P. S., and Han, J. (2003). Mining
concept-drifting data streams using ensemble classi-
fiers. In Proceedings of the 9th International Con-
ference on Knowledge Discovery and Data Mining
(KDD’03), pages 226–235, Washington, DC.
AN ADAPTIVE SELECTIVE ENSEMBLE FOR DATA STREAMS CLASSIFICATION
145
