
LEARNING FROM DEMONSTRATION
Automatic Generation of Extended Behavior Networks for Autonomous Robots
from an Expert’s Demonstration
Stefan Czarnetzki, S
¨
oren Kerner and Patrick Szcypior
Robotics Research Institute, Section Information Technology, TU Dortmund University, 44221 Dortmund, Germany
Keywords:
Extended behavior networks, Learning, Demonstration.
Abstract:
The recent research focus on autonomous mobile robots has greatly improved their capability to perform
complex tasks, making it more and more difficult to design eligible behavior manually. Therefore this paper
presents an algorithm to automatically derive a behavior network from demonstration by an expert. Different
tasks are evaluated to proof the generalizability and robustness of the proposed demonstration approach.
1 INTRODUCTION
Robotics commonly refers to behavior as deriving the
suitable motion from the current cognition to act pur-
posefully. Due to hardware improvements of mod-
ern autonomous robots the complexity of observa-
tions and possible actions is rising, leading obviously
to a higher behavior complexity. This places classical
methods of Artificial Intelligence at a disadvantage,
since the majority of these approaches try to reason
based on logic or knowledge bases. While the latter
would require an increasing amount of data and ex-
pert knowledge the same rise in complexity renders a
pure logical reasoning nearly impossible to handle for
mobile hardware. Thus the need for new solution to
design robotic behavior arises to scope with the new
fields of operation (see for instance (Arkin, 1999) and
(Brooks, 1990)). Being just one example, Behavior
Networks were proposed to develop a mechanism to
reliably select actions even in highly complex and dy-
namic environments, while still being intuitively com-
prehensible.
Developing behavior manually is sufficient for
reasonable tasks but becomes more and more difficult
with rising complexity. As a consequence application
of automatic learning techniques to robotics is ever-
more appealing. Behavior learning distinguishes be-
tween online and offline approaches. Although being
able to adapt behavior during execution would be very
desirable to react to errors, modern robotics hardware
lags the computational power to do so. Thus this pa-
per will limit itself to offline learning.
Those machine learning techniques can further be
roughly divided in classes of Supervised, Unsuper-
vised and Reinforcement learning. While all these
have in common that they try to generalize useful ac-
tions from a given database they differ in their applied
technique. Although all these strategies have been
successfully applied to different areas of robotics they
have a common disadvantage in this field of applica-
tion. More or less all approaches try to reason useful
actions by letting the robot itself experiment. On the
one hand this is a rather time consuming process and
on the other hand is likely to result in the robot choos-
ing a bad action at one point over the course of time.
While some might just result in a worse result of the
tasks, some of these actions might be harmful to the
hardware of the robot. To prevent such actions before-
hand it’s desirable to combine robotic machine learn-
ing with human interaction, not just by supervision of
the process but also by learning from demonstration.
Section 2 gives a summary over extensions to the
mentioned Behavior Networks providing the funda-
mental algorithms of this paper. In the following sec-
tion 3 further methods to enable the behavior to be
derived from human demonstration are presented and
experimentally tested and evaluated in section 4.
2 EXTENDED BEHAVIOR
NETWORKS
This section gives a brief overview of Behavior Net-
works which were first introduced by Maes in (Maes,
1989) and Extended Behavior Networks as in (Pinto
394
Czarnetzki S., Kerner S. and Szcypior P..
LEARNING FROM DEMONSTRATION - Automatic Generation of Extended Behavior Networks for Autonomous Robots from an Expert’s Demonstration.
DOI: 10.5220/0003184503940400
In Proceedings of the 3rd International Conference on Agents and Artificial Intelligence (ICAART-2011), pages 394-400
ISBN: 978-989-8425-40-9
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

and Alvares, 2005) or (Dorer, 2010).
Behavior networks define a representation of the
robot’s knowledge about its interaction with the
world. For given objectives this allows a rational
choice of an appropriate action. This knowledge base
is given in form of a network where each node ex-
presses a certain competence M or goal G. A com-
petence represents the knowledge about an action, i.e.
which change in the current world state is expected
by performing the action and which prerequisites are
required for the action to be executed.
Extended Behavior Networks are a means to carry
out behavior selection in dynamic and continuous do-
mains. Goals are explicitly situation-dependent. They
also allow parallel execution of actions by explicitly
modeling a set of resources R. Actions using disjoint
subsets of resources consequently do not conflict. The
resulting behavior network is given by (G, M, R, Π)
with Π being a set of parameters and the directed
graph N = (G∪M, K
+
, K
−
). The nodes are connected
by activating and inhibiting links, K
+
and K
−
, respec-
tively, according to their prerequisites and expected
consequences. The latter are originally described us-
ing boolean variables: a set of variables which need
to be true as prerequisites, and two lists for the con-
sequences, one for variables expected to become true
and one for those expected to become false. An acti-
vating link exists from a node x
1
to node x
2
if a pre-
requisite of x
1
will be fulfilled by the execution of x
2
.
Inhibiting links exist for the reverse case.
2.1 Network Definition
The description of the robot’s surrounding world us-
ing only “crisp” boolean logic however is insufficient
for more complex real-world scenarios. Robot per-
ception and world modeling usually involves real val-
ues of positions and directions with varying uncer-
tainties. For the purpose of a more appropriate world
state representation while keeping close to classical
behavior network specification a restricted fuzzy log-
ical system is employed in the presented approach.
Let P be the set of all statements and S the set of all
possible world states, then
τ : P × S → [0, 1] (1)
assigns truth values between 0 and 1 to statements for
a current world state estimation. In the following a
multi-valued logic L = (P, ¬, ∧) is defined. The nega-
tion of a statement p ∈ P for a world state estimation
s ∈ S is given by equation 2.
τ(¬p, s) = 1 − τ(p, s) (2)
The conjunction of statements is given by the operator
∧ and equation 3, where may be any T-conorm.
τ(p
1
∧ p
2
, s) = τ(p
1
, s) τ(p
2
, s) (3)
In the following is chosen to be T
min
(a, b) =
min(a, b) which fulfills the necessary properties for
a T-conorm.
The robot’s objectives are given in form of goal
nodes G. Those consist of a world state t to be
achieved and a static and dynamic relevance. t is ex-
pressed in L and handled equivalently to the prerequi-
sites of competence modules concerning the linkages
of the extended behavior network. The static rele-
vance i ∈]0, 1] adjusts the overall importance of the
objective. The dynamic relevance rel depends on the
current world state, i.e. the goal only becomes impor-
tant for a truth value above zero for a certain statement
specified in L.
As mentioned above, the set of competence mod-
ules M represents the robot’s knowledge enabling it
to employ rational behavior. Each competence mod-
ule is made up of an action b ∈ B, a prerequisite c
expressed in L that must be true for the action to be
executable, a set Res ⊆ R of needed resources, a set
E of effect pairs and an activation value a. An effect
pair (e f f , ex) consists of a statement e f f ∈ P and the
probability ex = P(e f f |c) of e f f coming true after
execution. A competence is therefore executable if c
is true, all resources Res are available and the activa-
tion value a is at least as big as the biggest activation
threshold of all necessary resources.
Edges in a behavior network express relations be-
tween nodes which influence each other. Each ef-
fect of a competence module x
i
causes relations to
all other nodes x
j
whose prerequisite c includes the
statement e f f . If the signs of e f f in c and the effect
match, then there is an activating link from x
j
to x
i
.
Otherwise the edge is an inhibiting link.
Finally there is the tuple Π = (β, γ, δ, θ, Θ) of pa-
rameters controlling activity distribution, propagation
and thresholds. β ∈ [0, 1[ controls the inertia of com-
petence modules, i.e. the trade-off between reactivity
and robustness determining how long activated com-
petence modules are staying active. γ, δ ∈ [0, 1[ de-
termine global weights for activating and inhibiting
links, respectively. θ ∈]0, ˆa] is the maximum activa-
tion threshold used as an initial value for activation
thresholds of resources with ˆa =
|G|
1−β
as the maximum
possible activation of a competence module. Θ ∈]0, 1[
controls the reduction of activation thresholds per it-
eration. Both θ and Θ control how much “foresight”
the robot employs when choosing its action. This will
be described more detailed in the next section.
LEARNING FROM DEMONSTRATION - Automatic Generation of Extended Behavior Networks for Autonomous
Robots from an Expert's Demonstration
395

2.2 Activation Distribution and Action
Decision
Using an extended behavior network an autonomous
agent can choose actions evaluating the maximum ex-
pected benefit based on the current situation and a set
of objectives. The normalized benefit of each goal is
assigned by
u(rel, i) = (τ(rel, s) · i)
2p
(4)
with a parameter p ∈]0, 1] controlling the agents
readiness to take chances. Choosing p =
1
2
con-
forms to action decisions based on rational choice
theory. p >
1
2
results in more risky decisions while
p <
1
2
tends to more conservative decisions according
to (Dorer, 2010).
In contrast to the Behavior Networks originally
proposed by Maes (Maes, 1989) activation potential
only originates from goal nodes ensuring a decision
process based only on expected benefit. A compe-
tence module receives activation from a goal if one of
its effects match a precondition of this goal and both
statements have the same sign, i.e. both are atoms
or both are negated atoms. A competence is inhib-
ited if exactly one of the atoms is negated. The same
holds for activating and inhibiting links between com-
petence modules, but dependent on the precondition’s
truth value: the less a precondition is satisfied, the
more activation is spread to modules which are ex-
pected to make this precondition come true. Thus un-
satisfied preconditions of modules with high activa-
tion values become increasingly demanding subgoals
themselves. For a detailed description of the func-
tions defining the activation propagation see (Dorer,
1999). For each module the activation values from
different goals are calculated separately and only the
highest absolute maximum activation a
t
m
k
g
i
from acti-
vating and inhibiting links is taken into account, i.e.
following only the strongest path. The final activation
of a module m
k
at time t is
a
t
m
k
= β · a
t−1
m
k
+
∑
i
a
t
m
k
g
i
. (5)
The action selection is done by iteratively prop-
agating activation through the behavior network, a
function h(a
t
m
k
, e
m
k
) combines the module’s activation
a
t
m
k
and its executability e
m
k
= τ(d
k
, s), and decreas-
ing all θ
r
by Θ until h(a
t
m
k
, e
m
k
) is big enough for a
competence module to claim the resources and be ex-
ecuted, in which case the θ
r
are reset for the next time
step’s action selection.
3 LEARNING BY
DEMONSTRATION
This section presents the behavior learning of au-
tonomous agents from an expert’s demonstrations by
means of automatic generation of an parametrized ex-
tended behavior network out of recorded demonstra-
tion data. An expert needs to demonstrate the correct
behavior for a variety of situations so that the pro-
cess of learning can be able to generalize. This has
to be done for every objective separately. The deduc-
tion of goals themselves from demonstrated behavior
is not covered here. Likewise the difficulty of map-
ping effects to one of several parallel executed actions
is neglected here by only allowing one action at a time
to be executed by the expert remotely controlling the
agent.
The demonstration result is several sequences of
demonstration pairs d
t
= (l
t
, b
t
) ∈ D of current world
states l
t
and behavior choices b
t
. l
t
is a statement in
L made up of the atoms with the biggest acceptance
value τ(p
s
i
, s
t
) for each perception.
l
t
= p
s
1
∧ ··· ∧ p
s
n
(6)
The effects of an action must be estimated using a
transition function
T (l
t
, b
t
) = z
t
(7)
to find the earliest state l
t+i
with i > 0 where l
t
l
t+i
.
Note that due to the multi-valued logic of L this
change just needs to an change in a truth value big-
ger than a certain threshold.
In the following the direct transformation of those
demonstration pairs to competence modules will be
described. Then induction will be introduced as a
matter of generalization and decision trees will be
used as an intermediate step for the final knowledge
representation. Finally an approach is presented to
derive an extended behavior network from decision
trees and a set of demonstration pairs.
The trivial approach to generate a behavior net-
work out of the set of demonstration pairs is to create
a new competence module for each occurrence of a
new combination of precondition and action choice.
An effect can be assigned using the transformation
function of equation 7 assuming total confidence into
this effect since no knowledge about its probability is
available at this point. Note that due to the described
choice of l
t
it does not contain all atoms of L, but still a
separate competence module is needed for every new
situation to result in a complete description because
no generalization is applied.
To reduce the number of necessary competence
modules a method is required to find the smallest
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
396

preconditions indicating a behavior choice. Such
hypotheses can be generated using a subset of the
demonstration pairs and validated of falsified using
a different subset. This is commonly done by in-
ferring a probability model using methods such as
Bayesian learning, kernel machines or neuronal net-
works (Hertzberg and Chatila, 2008).
Decision trees are classification methods in form
of trees with inner nodes commonly representing bi-
nary decisions and leaves representing the classifi-
cation result, i.e. the behavior choice. Generating
a decision tree in analog to the trivial behavior net-
work generation above and applying pruning after-
wards would result in a correct classification as long
as the demonstration pairs do not contain any conflict-
ing choices.
Finding the smallest decision tree as the most
generalizing hypothesis employs reasoning about the
information gain of the different symbols for vari-
ous subsets of demonstration pairs. The Gini-index
is a common criterion for the inequality of dis-
tributions (Kotsiantis, 2007). Most algorithms in
this domain are based on the Iterative Dichotomiser
3 (ID3) algorithm which is a top-down induction
method (Quinlan, 1987) or any of the later versions
like the C4.5 algorithm (Quinlan, 1993) which is the
basis for the implementation used in this approach.
The full algorithm to generate an extended be-
havior network from demonstration pairs is as fol-
lows. A generalized decision tree is generated from
the demonstration pairs using the C4.5 algorithm with
a parametrization limiting the tree’s growth while en-
suring that the vast majority of the demonstrations are
classified correctly. For each path in this decision tree
a competence node is added to the decision tree with
the leaf as its action choice while the inner tree nodes
form the competence node’s precondition. Note that
the decision tree itself could be used for a behavior
decision but that its output will not be equivalent to
the Behavior Networks output which instead aims at
robust rational decision planning instead of a simple
mapping of world state to action choice without re-
gard to previous choices or currently executed behav-
ior. Finally the effect pair can be generated using the
transition function of equation 7. In the simple di-
rect transformation described earlier the effect could
only be assumed as deterministic since each compe-
tence was based on a single demonstration. Now the
generalized competence can be used to find the sub-
set D
k
⊆ D of demonstration pairs matching the new
broader precondition and the effect probability can be
estimated using this subset.
Thus all parts of the competence modules are
specified. These modules represent the robot’s knowl-
edge about its behavior choices and their influence
and consequences in the world. Together with the
given goals the extended behavior network is com-
plete and was generated only from a specialist’s
demonstrations. The only specification remaining is
about the set Π of 5 parameters described in section 2
which need to be defined by the specialist to find a
trade-off between reactivity and robustness.
4 EVALUATION
To proof the concept of the proposed algorithm an ex-
perimental setup is chosen addressing two problems
taken from the RoboCup
1
. Playing soccer with hu-
manoid robots combines a wide variety of modern
robotic problems. Being a benchmark for modern
autonomous robots application, choosing RoboCup
tasks yields the advantage of making results compa-
rable to other research studies. For the evaluation two
skills needed by a soccer robot are chosen - approach-
ing a ball and avoiding obstacles. These cover the ap-
plication of object recognition, localization, precise
motion execution and interaction with objects. The
outcome of the experiments is easy to rate and fur-
thermore both experiments can be combined to fur-
ther test the generalization of the proposed approach.
Testing an algorithm based on human interaction
requires a certain amount of demonstrations to be rep-
resentative. Thus the evaluation of the proposed algo-
rithm is conducted utilizing a 2D simulator rather than
a real robotic platform. As an advantage this allows
a better comparison and more precise analysis of the
results. The expert can teach the simulator by using
a joystick as an input device. To reduce the complex-
ity of the behavior network the possible actions are
discretized to walk straight, turn left by 17
◦
and turn
right by 17
◦
. The simulator provides the robot with
precise perceptions which can be altered by adding
Gaussian noise.
The tested Extended Behavior Networks are de-
rived from demonstration as described in section 3.
The parameters are chosen to be γ = 0.9, β = 0.5,
δ = 0.8, θ = 0.6 and Θ = 0.9 (compare (Pinto and
Alvares, 2005)). The underlying decision trees are
developed from demonstration pairs utilizing the pro-
gram RapidMiner
2
. In addition these trees are chosen
as a behavior to be compared to the Extended Behav-
ior Networks.
Experiment 1 evaluates the learning of the soccer
skill go to ball. 100 robot positions are randomly
1
http://www.robocup.org
2
http://www.rapidminer.com
LEARNING FROM DEMONSTRATION - Automatic Generation of Extended Behavior Networks for Autonomous
Robots from an Expert's Demonstration
397
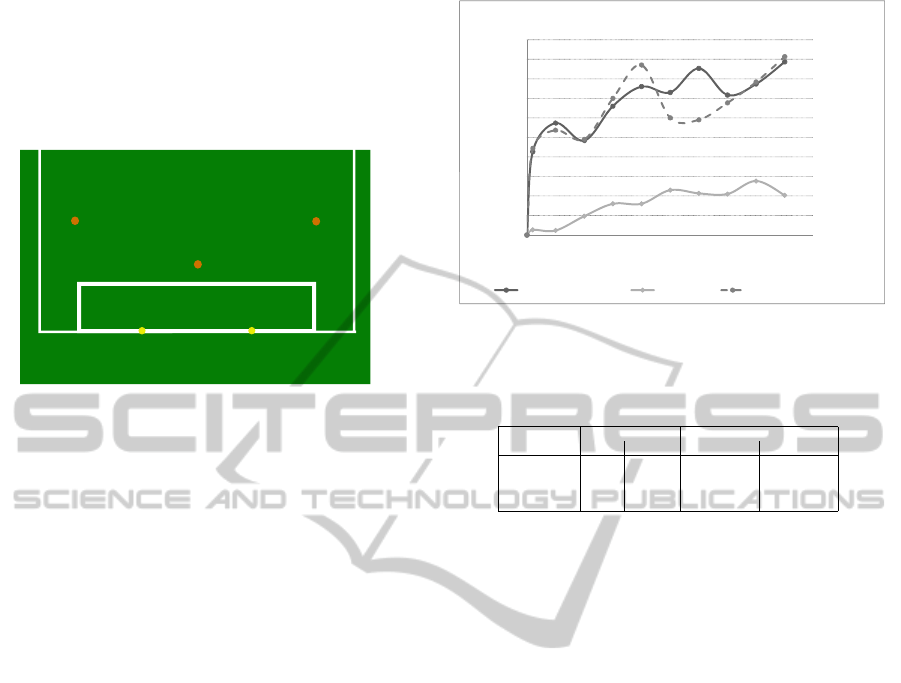
generated with the properties robot.x = −100 mm,
robot.y = [−2000 mm, 2000 mm] and robot.θ =
[−90
◦
, 90
◦
]. For each of the those starting positions
an expert demonstrates go to ball for three different
fixed ball placements (see figure 1) resulting in a total
of 300 demonstrations.
Figure 1: The different ball positions.
Another set of 100 different situations is gener-
ated to evaluate the learned skill. This time robot.x
is also chosen randomly from [−1000 mm, 100 mm]
and the ball is also positioned randomly with
ball.x = [750 mm, 2500 mm] and ball.y =
[750 mm, 2500 mm].
The utilized method to discretize the world state
is significant for the resulting behavior network. Thus
the experiment evaluates two different approaches.
Fayyad and Irani (Fayyad and Irani, 1993) propose a
automated method of supervised entropy-based dis-
cretization particularly designed to learn decision
trees. This approach is applied and compared to a
manual discretization realized by an expert. These
two Behavior Networks are modeled to be composed
only of one resource. Since the robot is capable of an
omni-directional walk rotation and translation can be
combined enabling the robot to utilize two resources,
which is done in another trial.
The overall success rates of the tested behaviors
can be found in figure 2. Table 1 compares the su-
pervised observation discretization based on Fayyad
and Irani to the expert tuning. Using the supervised
discretization in combination with the decision tree
achieves always better results than combining it with
manual discretization while the opposite is true for
the Extended Behavior Networks. The network prof-
its from the higher number of competencies, which
still generalize the situation to achieve way better re-
sults. This enables adjustment to error in demonstra-
tion which are clearly committed by the expert by not
being able to always choose the exact same action in
the same world state. This accommodation to error
results in a superiority of the demonstrated Extended
Behavior Networks. Comparing the 1-resource net-
89%
28%
91%
40%
50%
60%
70%
80%
90%
100%
successrate
89%
28%
91%
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
0100200300400
successrate
#ofdemonstrations
1Ͳresourcebaviornetwork decissiontree 2Ͳresourcebehaviornetwork
Figure 2: Success rates of Experiment 1.
Table 1: Comparison between discretization methods of a
behavior network (decision tree).
# situations # competencies success
F&I expert F&I expert
90 3 138 39% (39%) 48% (10%)
180 14 175 48% (31%) 76% (16%)
270 23 193 21% (31%) 85% (21%)
360 33 213 23% (35%) 77% (28%)
work to the 2-resource network shows tendency to
slightly better overall results when utilizing two re-
sources. But figure 2 also shows a drop in success
of the 2-resource network around the demonstration
mark of 250. Thus a clear superiority can not be
proofed.
Experiment 2 evaluates the skill obstacle avoid-
ance. An obstacle is placed on the center spot of the
field (x = 0 mm,y = 0 mm). The expert avoids the ob-
stacle while still trying to head for the ball, which is
placed at position ball.x = 3000 mm, ball.y = 0 mm.
The robot position is determined along the path to the
ball obstructed by the obstacle. It is randomized by
the distance d = [150 mm, 450 mm] to the obstacle
and the robots alignment Θ = [−45
◦
, 45
◦
] towards
the object. The demonstration is conducted 400 times.
The goal only takes the distance to the object in con-
sideration, which should be higher than 500 mm. The
resulting behavior network is tested with another set
of 100 randomly generated situations.
The outcome of the second experiment can be
found in figure 3 showing also good results utiliz-
ing the proposed demonstration approach. Analyzing
the results of these experiments proof that, given a
proper number of demonstrations, the presented al-
gorithm allows the robot to learn general skills by
demonstrating special situations. But this second ex-
periment does not demonstrate the same benefit of
using multiple resources simultaneously. While the
evaluation reveals that success is achieved faster mod-
eling two resources, which is evident since the robot
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
398

94%
26%
74%
40%
50%
60%
70%
80%
90%
100%
successrate
94%
26%
74%
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
050100150200250300350400
successrate
#ofdemonstration
1Ͳresourcebaviornetwork decissiontree 2Ͳresourcebehaviornetwork
Figure 3: Success rates of Experiment 2.
can execute actions simultaneously, activating a mul-
titude of resources can lead to unforeseen effects. The
discussed drop in success during the first experiment
suggests the same conclusion, thus a general advise is
not possible at this time.
Extended Behavior Networks are designed with
the possibility to model different contrary goals.
Therefore Experiment 3 is designed to test this char-
acteristic by combining the Behavior Networks of Ex-
periment 1 and 2. As an experimental setup, robot and
ball are placed according to the setup of Experiment
1. In addition 6 / 8 / 10 obstacles are put randomly be-
tween robot and ball. A set of 300 situations is gener-
ated and used as a test for the demonstrated behavior.
The importance of the obstacle avoidance skill is set
to i = 1.0 and that of go to ball is set to i = 0.6 to
model the skill priority.
Table 2: Results of Experiment 3.
# obstacles success without avoidance success with avoidance
6 46% 59%
8 40% 52%
10 31% 53%
Table 2 demonstrates the results of the combina-
tion experiment. It can be seen that even without the
avoidance skill the robot sometimes can successfully
complete the experiment. Since the placement of the
obstacles is random, this can be explained by a setup
without an obstacle blocking the path to the ball. With
more obstacles placed on the field this occurs less of-
ten. Combining goto ball with avoid obstacle results
in a clear increase of the robots success rate. The less
from ideal results can mostly be explained by an in-
sufficient demonstrations taking into account the na-
ture of the experiment. First of all due to the random-
ness of the obstacle placements there are some setups
in which the obstacles are too close to each other for
the robot to pass through without violating the goal.
This is a situation not taught by the obstacle avoid-
ance skill. In addition some times the avoidance of an
obstacle leads to a robot position close to the ball, but
not facing it. This also is not covered by the demon-
strated skill of Experiment 1 leading to a failure of the
experiment.
While the described experiments display the ad-
vantage of the demonstration approach they are con-
ducted with ideal percepts. To test the robustness of
the proposed algorithm Experiment 1 is repeatedly
conducted with increasing normally distributed noise
added to the input.
40%
50%
60%
70%
80%
90%
100%
sucessrate
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
0% 20% 40% 60% 80% 100%
sucessrate
variance
behaviornetwork dessisiontree
Figure 4: Results of Experiment 4.
Figure 4 demonstrates a comparison of the robust-
ness between the extended behavior network and the
decision tree. While the success rate of the extended
behavior network decreases with rising noise ratio as
expected, it does so more slowly than the decision
tree. Even with a noise ration of 15 percent the suc-
cess rate stays above 70 percent allowing the algo-
rithm to be called robust.
5 CONCLUSIONS
This paper presented an algorithm to automatically
derive a behavior network imitating a skill demon-
strated by an expert. The theoretical concept has
been tested in simulation mimicking skills needed by
a soccer robot participating in the RoboCup. The
conducted experiments proof the possibility to apply
skills, learned from demonstrating a specific behav-
ior, successfully to different situations, requiring the
same skill. But the results indicate the need for a
certain amount of demonstrations to achieve a rea-
sonable success rate, depending on the complexity of
the task. The influence of the task complexity could
be shown by combining two basic skills to solve a
task not learned by the robot. While principally being
LEARNING FROM DEMONSTRATION - Automatic Generation of Extended Behavior Networks for Autonomous
Robots from an Expert's Demonstration
399

able to solve this assigned task the rising complexity
may result in situations fundamentally different and
not covered by demonstration. Finally the robustness
of the approach has been proven by testing the be-
havior network against a simulation of noisy world
states, indicating a transferability from simulation to
the real robot, but this has still to be proven in future
experiments. Especially due to the necessity of high
quantity of demonstration the desire arises to combine
demonstrations in reality and simulation to reduce the
stress of the robotic hardware.
REFERENCES
Arkin, R. C. (1999). Behavior-based robotics, intelligent
robots and autonomous agents series, mit press, cam-
bridge, mass., 1998, xiv+491 pp, isbn 0-262-
01165-4. Robotica, 17(2):229–235.
Brooks, R. A. (1990). Elephants don’t play chess. Robotics
and Autonomous Systems, 6:3–15.
Dorer, K. (1999). Behavior networks for continuous do-
mains using situation-dependent motivations. In In
Proc. 16th Int. Joint Conf. on Artificial Intelligence
(IJCAI), pages 1233–1238.
Dorer, K. (2010). Modeling human decision making us-
ing extended behavior networks. In RoboCup 2009:
Robot Soccer World Cup XIII, volume 5949 of Lecture
Notes in Computer Science, pages 81–91. Springer
Berlin / Heidelberg.
Fayyad and Irani (1993). Multi-interval discretization of
continuous-valued attributes for classification learn-
ing. In Proceedings of the International Joint Con-
ference on Uncertainty in AI, pages 1022–1027.
Hertzberg, J. and Chatila, R. (2008). AI Reasoning Meth-
ods for Robotics. In Springer Handbook of Robotics,
pages 207–223. Springer Berlin Heidelberg.
Kotsiantis, S. B. (2007). Supervised machine learning:
A review of classification techniques. Informatica,
31:249–268.
Maes, P. (1989). How to do the right thing. Connection
Science Journal, 1:291–323.
Pinto, H. and Alvares, L. (2005). An extended behavior net-
work for a game agent: An investigation of action se-
lection quality and agent performance in unreal tour-
nament. 5TH International Working Conference on
Intelligent Virtual Agents.
Quinlan, J. R. (1987). Simplifying decision trees. Int. J.
Man-Mach. Stud., 27(3):221–234.
Quinlan, J. R. (1993). C4.5: programs for machine learn-
ing. Morgan Kaufmann Publishers Inc., San Fran-
cisco, CA, USA.
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
400
