IN YOUR INTEREST

Objective Interestingness Measures for a Generative Classiﬁer

Dominik Fisch, Edgar Kalkowski, Bernhard Sick

Computationally Intelligent Systems Lab, University of Applied Sciences Deggendorf, Deggendorf, Germany

Seppo J. Ovaska

Aalto University, School of Science and Technology, Espoo, Finland

Keywords:

Classiﬁcation, Data mining, Interestingness.

Abstract:

In a wide-spread deﬁnition, data mining is termed to be the “non-trivial process of identifying valid, novel,

potentially useful, and ultimately understandable patterns in data”. In real applications, however, usually only

the validity of data mining results is assessed numerically. An important reason is that the other properties are

highly subjective, i.e., they depend on the speciﬁc knowledge and requirements of the user. In this article we

deﬁne some objective interestingness measures for a speciﬁc kind of classiﬁer, a probabilistic classiﬁer based

on a mixture model. These measures assess the informativeness, uniqueness, importance, discrimination,

comprehensibility, and representativity of rules contained in this classiﬁer to support a user in evaluating data

mining results. With some simulation experiments we demonstrate how these measures can be applied.

1 INTRODUCTION

Data mining (DM)—today typically used as a syn-

onym of knowledge discovery in databases (KDD)—

deals with the detection of interesting patterns (e.g.,

regularities) in often huge amounts of data and the

acquisition of knowledge (e.g., classiﬁcation rules) in

application ﬁelds such as marketing, fraud detection,

drug design, and many more. In a well-known deﬁni-

tion, it is termed to be the “non-trivial process of iden-

tifying valid, novel, potentially useful, and ultimately

understandable patterns in data” (Fayyad et al., 1996).

But, how can this “interestingness” of patterns be as-

sessed, in particular numerically? It is obvious that

attributes such as novel, useful, and understandable

are highly subjective as they depend on the particular

needs and the previous knowledge of the data miner.

Thus, usually only the validity of patterns or extracted

knowledge is assessed numerically in order to get an

objective validation of DM results.

In this article, we focus on some other attributes

of data mining results that can be measured numeri-

cally. They are objective on the one hand and related

to attributes such as novelty, usefulness, and under-

standability on the other. For that purpose, we use a

speciﬁc classiﬁer, a classiﬁer based on probabilistic

(Gaussian) mixture models (CMM), see also (Fisch

and Sick, 2009; Bishop, 2006). CMM contain rules

that have a form similar to that of fuzzy rules but

they must be interpreted in a probabilistic way. A

rule premise aims at modeling a data cluster in the in-

put space of a classiﬁer, while the conclusion assigns

that cluster to a certain class. Our new interestingness

measures assess the informativeness, uniqueness, im-

portance, discrimination, comprehensibility, and rep-

resentativity of rules contained in a CMM in order to

support a user in evaluating DM results.

In the remainder of the article we brieﬂy discuss

some related work in Section 2. Then, we describe

the classiﬁer and introduce the various interestingness

measures in Section 3. Three case studies in Section

4 show how these measures could be applied. Finally,

we brieﬂy conclude in Section 5 and also give an out-

look to future work.

2 RELATED WORK

Basically, there are subjective and objective interest-

ingness measures that are used to assess rules ex-

tracted from data in a DM process, see, e.g., (Hilder-

man and Hamilton, 2001; McGarry, 2005).

Objective measures are solely based on an anal-

414

Fisch D., Kalkowski E., Sick B. and J. Ovaska S..

IN YOUR INTEREST - Objective Interestingness Measures for a Generative Classiﬁer.

DOI: 10.5220/0003186404140423

In Proceedings of the 3rd International Conference on Agents and Artiﬁcial Intelligence (ICAART-2011), pages 414-423

ISBN: 978-989-8425-40-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

ysis of the extracted knowledge. These interesting-

ness measures are based, for example, on informa-

tion criteria or on data-based evaluation techniques.

Typical examples are Akaike’s information criterion

or the Bayesian information criterion on the one hand

and statistical measures such as sensitivity, speciﬁcity,

precision etc. computed in a cross-validation or a

bootstrapping approach on training/test data on the

other (cf. (Duda et al., 2001; Tan et al., 2004), for

instance). Other criteria that assess the complexity of

rules or rule sets are, e.g., a rule system size measure

(gives the overall number of rules in the rule system),

a computational complexity measure (CPU time re-

quired for the evaluation of a rule or a rule system),

a rule complexity measure (number of attributes that

are tied together in a rule), a mean scoring rules mea-

sure (average number of rules that have to be applied

to come to a conclusion), a fuzzy quality measure (for

terms such as “bad”, “average”, or “very good” that

are associated with rules), the information gain for

association rules (Atzmueller et al., 2004; Taha and

Ghosh, 1997; Nauck, 2003; Hebert and Cremilleux,

2007). Also, measures are combined (e.g., in form

of a weighted sum) in some cases (Atzmueller et al.,

2004; Taha and Ghosh, 1997).

Subjective measures consider additional knowl-

edge about the application ﬁeld and / or information

about the user of a DM system, e.g., skills and needs

(Piatetsky-Shapiro and Matheus, 1994; Padmanab-

han and Tuzhilin, 1999). Subjective interestingness

measures mentioned in the literature are, for exam-

ple, novelty (Basu et al., 2001; Fayyad et al., 1996),

usefulness (Fayyad et al., 1996), understandability

(Fayyad et al., 1996), actionability (Silberschatz and

Tuzhilin, 1996), and unexpectedness (Padmanabhan

and Tuzhilin, 1999; Silberschatz and Tuzhilin, 1996;

Di Fiore, 2002; Liu et al., 2000). The existing mea-

sures use different techniques to represent informa-

tion about the human domain experts and they also

greatly depend on the respective kind of knowledge

representation, e.g., Bayesian networks, fuzzy classi-

ﬁers, or association rules.

3 METHODOLOGICAL

FOUNDATIONS

In this section we will ﬁrst present the generative clas-

siﬁer paradigm. A generative classiﬁer aims at mod-

eling the processes underlying the “generation” of the

data (Bishop, 2006). We use probabilistic techniques

for that purpose. Then, we will describe our new in-

terestingness measures.

3.1 Probabilistic Classiﬁer CMM

3.1.1 Deﬁnition of CMM

The classiﬁers we are using here are probabilistic

classiﬁers, i.e., classiﬁers based on mixture models

(CMM). That is, for a given D-dimensional input pat-

tern x

we want to compute the posterior distribution

p(c|x

), i.e., the probabilities for class membership

(with classes c ∈ {1,...,C}) given the input x

. To

minimize the risk of classiﬁcation errors we then se-

lect the class with the highest posterior probability (cf.

the principle of winner-takes-all), for instance. Ac-

cording to (Fisch and Sick, 2009), p(c|x) can be de-

composed as follows:

p(c|x) =

p(c)p(x|c)

p(x)

p(c)

∑

i=1

p(i|c)p(x|c, i)

p(x)

(1)

where

p(x) =

∑

p(c

)

∑

i=1

p(i|c

)p(x|c

,i). (2)

This approach is based on C mixture density mod-

els

∑

i=1

p(x|c,i)p(i|c), one for each class. Here, the

conditional densities p(x|c,i) with c ∈ {1, . . . ,C} and

i ∈ {1,...,I

} are called components, the p(i|c) are

multinomial distributions with parameters π

c,i

(mix-

ing coefﬁcients), and p(c) is a multinomial distribu-

tion with parameters γ

(class priors).

That is, we have a classiﬁer consisting of J =

∑

c=1

components, where each component is de-

scribed by a distribution p(x|c,i). To keep the no-

tation uncluttered, in the following a speciﬁc compo-

nent is identiﬁed by a single index j ∈ {1,...,J} (i.e.,

p(x| j)) if its class is not relevant.

Which kind of density functions can we use for

the components? Basically, a D-dimensional pattern

x may have D

cont

continuous (i.e., real-valued) di-

mensions (attributes) and D

cat

= D − D

cont

categori-

cal ones. Without loss of generality we arrange these

dimensions such that

x = (x

,...,x

cont

| {z }

continuous

cont

,...,x

| {z }

categorical

). (3)

Note that we italicize x when we refer to single di-

mensions. The continuous part of this vector x

cont

,...,x

cont

) with x

∈ R for all d ∈ {1,...,D

cont

}

is modeled with a multivariate normal (i.e., Gaussian)

distribution with center µ

µ and covariance matrix Σ

Σ.

That is, with det(·) denoting the determinant of a ma-

trix we use the model

IN YOUR INTEREST - Objective Interestingness Measures for a Generative Classifier

415

N (x

cont

|µ

µ,Σ

Σ) =

(2π)

cont

det(Σ

Σ)

exp



−0.5 (∆

cont

,µ

µ))



(4)

with the distance measure (matrix norm) ∆

)

given by

∆

) =

− v

)

−1

− v

). (5)

∆

deﬁnes the Mahalanobis distance of vectors

∈ R

cont

based on a D

cont

× D

cont

covariance

matrix M. For many practical applications, the use

of Gaussian components or Gaussian mixture models

can be motivated by the generalized central limit the-

orem which roughly states that the sum of indepen-

dent samples from any distribution with ﬁnite mean

and variance converges to a normal distribution as the

sample size goes to inﬁnity (Duda et al., 2001).

For categorical dimensions we use a 1-of-K

cod-

ing scheme where K

is the number of possible cat-

egories of attribute x

(d ∈ {D

cont

+ 1,...,D}). The

value of such an attribute is represented by a vector

= (x

,...,x

) with x

= 1 if x

belongs to cat-

egory k and x

= 0 otherwise. The classiﬁer models

categorical dimensions by means of multinomial dis-

tributions. That is, for an input dimension (attribute)

∈ {x

cont

,...,x

} we use

M (x

|δ

) =

∏

k=1

(6)

with δ

= (δ

,...,δ

) and the restrictions δ

≥ 0

and

∑

k=1

= 1.

We assume that the categorical dimensions are

mutually independent and that there are no dependen-

cies between the categorical and the continuous di-

mensions. Then, the component densities p(x| j) are

deﬁned by

p(x| j) = N (x

cont

|µ

,Σ

) ·

∏

d=D

cont

M (x

|δ

). (7)

3.1.2 Training of CMM

How can the various parameters of the classiﬁer be

determined? For a given training set X with N sam-

ples (patterns) x

it is assumed that the x

are inde-

pendent and identically distributed. First, X is split

into C subsets X

, each containing all samples of the

corresponding class c, i.e.,

= {x

belongs to class c}. (8)

Then, a mixture model is trained for each X

. Here,

we perform the parameter estimation by means of a

technique called variational Bayesian inference (VI)

which realizes the Bayesian idea of regarding the

model parameters as random variables whose distri-

butions must be trained (Fisch and Sick, 2009). This

approach has two important advantages over other

methods. First, the estimation process is more robust,

i.e., it avoids “collapsing” components, so-called sin-

gularities whose variance in one or more dimensions

vanishes. Second, VI optimizes the number of com-

ponents by its own. For a more detailed discussion on

Bayesian inference, and, particularly, VI see (Bishop,

2006). More details concerning the training algorithm

can be found in (Fisch and Sick, 2009).

At this point, we have found parameter estimates

for the p(x|c,i) and p(i|c), cf. Eq. (1). The parameters

for the class priors p(c) are estimated with

|X|

(9)

where |S| denotes the cardinality of the set S.

3.1.3 Rule Extraction from CMM

In some applications it is desirable to extract human-

readable rules from the trained classiﬁer. This is

possible with CMM if they are parametrized accord-

ingly. For the moment we focus on a single compo-

nent p(x| j) and omit the identifying index j. Basi-

cally, there are no restrictions necessary concerning

the covariance matrix Σ

Σ or the number of categories

. However, if the covariance matrix is forced to be

diagonal (i.e., assuming that there are no dependen-

cies between continuous input dimensions), the mul-

tivariate Gaussian N (x

cont

|µ

µ,Σ

Σ) can be split into a

product consisting of D

cont

univariate Gaussians ψ

with d ∈ {1, . . . , D

cont

}. A categorical dimension d ∈

cont

+1,...,D} can be simpliﬁed by only consider-

ing the n

“important” categories k

(i = 1,...,n

i.e., those with a probability δ

above the average

1/K

. The probabilities of these categories are renor-

malized and the remaining categories are discarded.

Then, a rule like the following can be extracted from

a component:

if x

is ψ

and . . . and x

cont

is ψ

cont

and (x

cont

= k

cont

+1)

or . . .

or x

cont

= k

cont

+1)

cont

)

and (x

= k

or . . . or x

= k

)

then c

is 0 and c

is 1 and . . .

The whole CMM can, thus, be transformed into

a rule set whose variables are the input variables (di-

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

416

mensions of the input variable x) and the output vari-

able c which represents the classes. The rule premises

are realized by conjunctions of the univariate Gaus-

sians ψ

(d = 1, . ..,D

cont

) and the simpliﬁed categor-

ical dimensions. The latter are modeled by disjunc-

tions of the categories. The conclusions (i.e., the class

membership) are given by the class-dependent GMM

to which the component p(x| j) belongs.

These rules enable reasoning based on uncertain

observations as shown in Eq. (1). The ﬁnal classiﬁ-

cation decision is obtained by superimposing the rule

conclusions weighted with the degree of membership

given by the rule premises, the mixing coefﬁcients

and the class priors. The extracted rules have a form

which is very similar to that of fuzzy rules, but they

have a very different (i.e., probabilistic) interpreta-

tion, cf. (Fisch et al., 2010).

A B C A B C

A B C

low

high

low high

Figure 1: Example of a Classiﬁer Consisting of Three

Rules.

Fig. 1 gives an example for such a classiﬁer con-

sisting of three components in a three-dimensional in-

put space. The ﬁrst two dimensions x

are continu-

ous and, thus, modeled by bivariate Gaussians whose

centers are described by the crosses (+). The ellipses

are level curves (surfaces of constant density) with

shapes deﬁned by the covariance matrices. Due to

the diagonality of the matrices these ellipses are axes-

oriented and the projection of the corresponding bi-

variate Gaussian onto the axes is also shown. The

third dimension x

is categorical. The trained distribu-

tion of categories is illustrated by the histogram next

to every component. For this CMM, the following

rule set can be extracted:

if x

is low and x

is high and (x

is A or x

is B)

then c

= 1 and c

= 0

if x

is high and x

is high and (x

is C)

then c

= 0 and c

= 1

if x

is high and x

is low

then c

= 1 and c

= 0

Of course, this readability is accomplished at the

cost of a limited modeling capability of the classiﬁer

(i.e., restricted covariance matrices and simpliﬁed cat-

egorical dimensions) and should, thus, only be used if

the application demands this kind of human-readable

rules.

3.2 Objective Interestingness Measures

for CMM

In the following we describe some new interesting-

ness measures that can be taken to assess a classiﬁer

based on CMM in an objective way. If the class a

component belongs to is not relevant for the assess-

ment, the component is identiﬁed by a single index

j ∈ {1,...,J}, i.e., p(x| j). Otherwise, it is explicitely

denoted with p(x|c,i). If sample data are needed to

evaluate a measure, we use the training data for that

purpose. In addition, classical performance measures

(e.g., classiﬁcation error on independent test data)

should be used. The knowledge we want to assess

is represented by the components of which the CMM

consists. We will use the term rule instead of com-

ponent only if we wish to explicitely extract human-

readable rules from the CMM.

3.2.1 Informativeness

A component of the CMM is considered as being very

informative if it describes a really distinct kind of pro-

cess “generating” data. To assess the informativeness

of a component numerically we use the Hellinger dis-

tance H(p(x),q(x)) of two probability densities p(x)

and q(x). Compared to other statistical distance mea-

sures such as the Kullback-Leibler divergence it has

the advantage of being bounded between 0 and 1. It

is deﬁned by

H(p(x), q(x)) =

1 − BC(p(x), q(x)), (10)

where BC(p(x),q(x)) denotes the Bhattacharyya co-

efﬁcient deﬁned by

BC(p(x), q(x)) =

p(x)q(x)dx. (11)

H(p(x), q(x)) is 0 if p(x) and q(x) describe the same

distribution and it approaches 1 when p(x) places

most of its probability mass in regions where q(x) as-

signs a probability of nearly zero and vice versa.

IN YOUR INTEREST - Objective Interestingness Measures for a Generative Classifier

417

Using Fubini’s theorem and considering the dis-

crete nature of the multinomial distribution, the Bhat-

tacharyya coefﬁcient of two components p(x| j) and

p(x| j

), as deﬁned in Eq. (7), can be computed by

BC(p(x| j), p(x| j

)) =

N (x

cont

|µ

,Σ

)N (x

cont

|µ

,Σ

)dx

cont

∏

d=D

cont

∑

k=0

M (e

|δ

)M (e

|δ

)

(12)

with e

being the k-th row of a K

×K

identity matrix

(i.e., we are iterating over all K

possible categories of

dimension d). The integral can be solved analytically

N (x

cont

|µ

,Σ

)N (x

cont

|µ

,Σ

)dx

cont

exp

−

(µ

− µ

)



+ Σ



−1

(µ

− µ

)

det(Σ

)det(Σ

)

det



+Σ



(13)

The informativeness of a component p(x| j) is

then determined by its Hellinger distance calculated

with respect to the “closest” component p(x| j

) ( j

j) contained in the CMM:

info(p(x| j)) = min

6= j

(H(p(x| j

), p(x| j)). (14)

3.2.2 Uniqueness

The knowledge modeled by the components within

a CMM should be unambiguous. This is measured

by the uniqueness of a component p(x|c,i) which re-

ﬂects to which degree samples belonging to different

classes are covered by that component. Let ρ

c,i

)

denote the responsibility of component p(x|c,i) for

the generation of sample x

c,i

) =

p(c)p(i|c)p(x

|c,i)

p(x

)

. (15)

Then, we deﬁne the uniqueness of rule p(x|c,i) by

uniq(p(x|c, i)) =

∑

∈X

c,i

)

∑

∈X

c,i

)

. (16)

3.2.3 Importance

The importance of a component measures the rela-

tive weight of a component within the classiﬁer. A

component p(x|c,i) is regarded as very important if

its mixing coefﬁcient weighted with the class prior

c,i

· p(c) is far above the average mixing coefﬁcient

π =

. To scale the importance of a component to

the interval [0,1] we use a boundary function that is

comprised of two linear functions. One maps all mix-

ing coefﬁcients that are smaller than the average to the

interval [0, 0.5] and the other maps all mixing coefﬁ-

cients that are larger than the average to [0.5,1]. The

importance of component p(x|c, i) is then computed

impo(p(x|c, i)) =

(

c,i

·p(c)

, π ≤ π



c,i

·p(c)

1−π

−

1−π

+ 1



, π > π

(17)

3.2.4 Discrimination

The discrimination measure evaluates the inﬂuence of

a component p(x|c, i) on the decision boundary—and,

thus, on the classiﬁcation performance—of the over-

all classiﬁer. To calculate the discrimination of com-

ponent p(x|c, i) we create a second CMM by remov-

ing p(x|c, i) from the original CMM and renormaliz-

ing the mixing coefﬁcients of the remaining compo-

nents. Then, we compare the achieved classiﬁcation

error on training data of the original CMM (E

with

) to

the classiﬁcation error of the CMM without compo-

nent p(x|c,i) (E

without

) weighted with the correspond-

ing class prior p(c):

disc(p(x|c, i)) =

without

− E

with

p(c)

. (18)

If required by a concrete application (e.g., in some

medical applications false positives are acceptable

whereas false negatives could be fatal), it is also possi-

ble to use more detailed measures such as sensitivity,

speciﬁcity, or precision to assess the discrimination of

a component.

3.2.5 Representativity

The performance of a generative classiﬁer highly de-

pends on how well it “ﬁts” the data. This kind of

ﬁtness is determined by the continuous dimensions

since we explicitely assume that the data distribu-

tion can be modeled by a mixture of Gaussian dis-

tributions. For the categorical dimensions we do not

assume any functional form. Therefore, the repre-

sentativity measure only considers the continous di-

mensions x

cont

. Again, we use the Hellinger dis-

tance H(p(x

cont

),q(x

cont

)), cf. Eq. (10), and measure

the distance between the true data distribution q(x

cont

)

and the model p(x

cont

) (i.e., the multivariate Gaussian

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

418

part), cf. Eq. (2) and (4). As for real-world data sets

the true underlying distribution q(x

cont

) is unknown,

it is approximated with a non-parametric density esti-

mator consisting of a Parzen window density estima-

tor:

q(x

cont

) =

∑

∈X

(2πh

)

conf

· exp



−

cont

− x

cont



(19)

Here, h is a user-deﬁned parameter whose value de-

pends on the data set X (Bishop, 2006). There are

a number of heuristics to estimate h. For instance,

in (Bishop, 1994) h is set to the average distance of

the ten nearest neighbors for each sample, averaged

over the whole dataset. This non-parametric approach

makes no assumptions about the functional form of

the underlying distribution. Therefore, we cannot use

Eq. (12) to calculate the Bhattacharyya coefﬁcient an-

alytically. However, it can be approximated with

BC(p(x), q(x)) ≈

∑

∈X

q(x

)

p(x

)q(x

). (20)

Note that we sum up over samples that are distributed

according to q (cf. so-called importance sampling

techniques).

Representativity measures the inﬂuence of a com-

ponent on the “goodness of ﬁt” of the model with

respect to the data distribution. To calculate the

representativity of component p(x| j) we again cre-

ate a second CMM without p(x| j) as described for

the discrimination measure. Then, we compare the

Hellinger distance of the CMM with (p

with

(x)) and

without (p

without

(x)) component p(x| j):

repr(p(x| j)) = (21)

H(p

without

(x),q(x)) − H(p

with

(x),q(x)).

3.2.6 Comprehensibility

Comprehensibility measures how well the compo-

nents (here referred to as rules) within the classiﬁer

can be interpreted by a human domain expert.

First, we claim that in a comprehensible classiﬁer

the overall number of rules J should be be low. There-

fore, we use the number of different rules as one of

three measures for comprehensibility.

Second, the number of different terms τ

for each

input dimension d should be low. For a categorical

dimension τ

is given by the number of categories n

forming the disjunctions:

∑

j=1

. (22)

For a continuous dimension d the number τ

different univariate Gaussians ϕ

d, j

is counted. To de-

cide whether two Gaussians should be regarded as be-

ing different or not, we use the Hellinger distance,

cf. Eq. (10), of the two Gaussians which should be

clearly below 0.01, for example, to regard two Gaus-

sians as being identical.

The overall classiﬁer is then assessed numerically

by averaging over all dimensions (both, categorical

and continuous):

τ =

∑

d=1

. (23)

Applying this measure to the example classiﬁer

shown in Fig. 1 gives τ

= 2, τ

= 2, and τ

= 3 which

in turn results in τ = 2.3.

d, j

dist(ϕ

d, j

)

Figure 2: Example of an Assessment of the Distinguisha-

bility of two Gaussians.

Third, to simplify the understanding of a rule set,

two different rules should be easy to distinguish. This

distinguishability is only determined for the continu-

ous dimensions d ∈ {1,...,D

cont

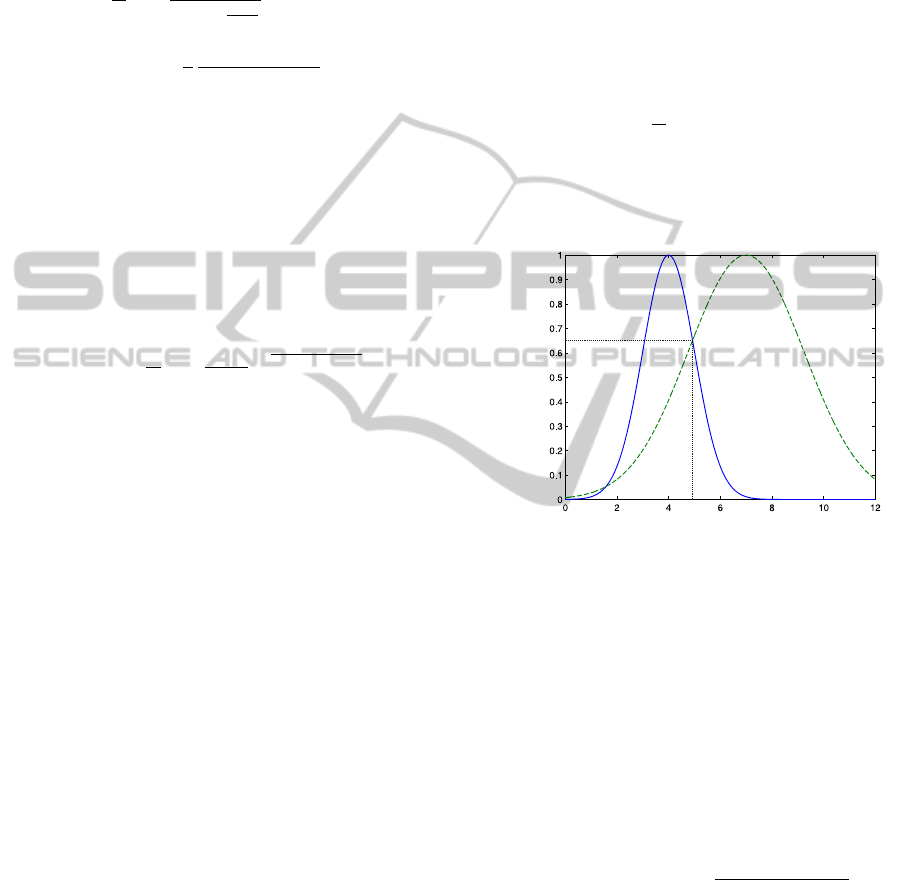
}. It is measured by

the ordinate value of the intersection point of two uni-

variate Gaussians ϕ

d, j

and ϕ

d, j

(the y-coordinate of

that intersection point which has an x-coordinate be-

tween the two means, to be precise), cf. Fig. 2. This

measure is restricted to the unit interval by omitting

the normalization coefﬁcients of the Gaussians in the

calculation which results in:

dist(ϕ

d, j

,ϕ

d,, j

) = 1 − exp

−

(µ

d, j

− µ

d, j

)

2 · (σ

d, j

+ σ

d, j

)

(24)

with dist(ϕ

d, j

,ϕ

d, j

) ∈ (0, 1]. Values higher than 0.3,

for example, could be regarded as desirable.

The distinguishability of the whole rule set is

given by the pair of rules which is most difﬁcult to

distinguish, i.e., the pair with the highest value of

dist(p(x| j), p(x| j

)).

IN YOUR INTEREST - Objective Interestingness Measures for a Generative Classifier

419

4 CASE STUDIES

In this section we demonstrate the application of our

proposed interestingness measures by means of three

publicly available data sets. The ﬁrst case study

serves as an illustrative example of the general usage

and characteristics of the measures. Then, we investi-

gates how restricting the classiﬁer in order to produce

human-comprehensible rules inﬂuences the classiﬁ-

cation performance. Finally, we show how some of

the interestingness measures can be used to automati-

cally prune classiﬁers.

4.1 “Clouds” Data Set

The ﬁrst case study uses the “clouds” data set from the

UCL/MLG Elena database (UCL, 2007). This two-

dimensional (both attributes are continuous) data set

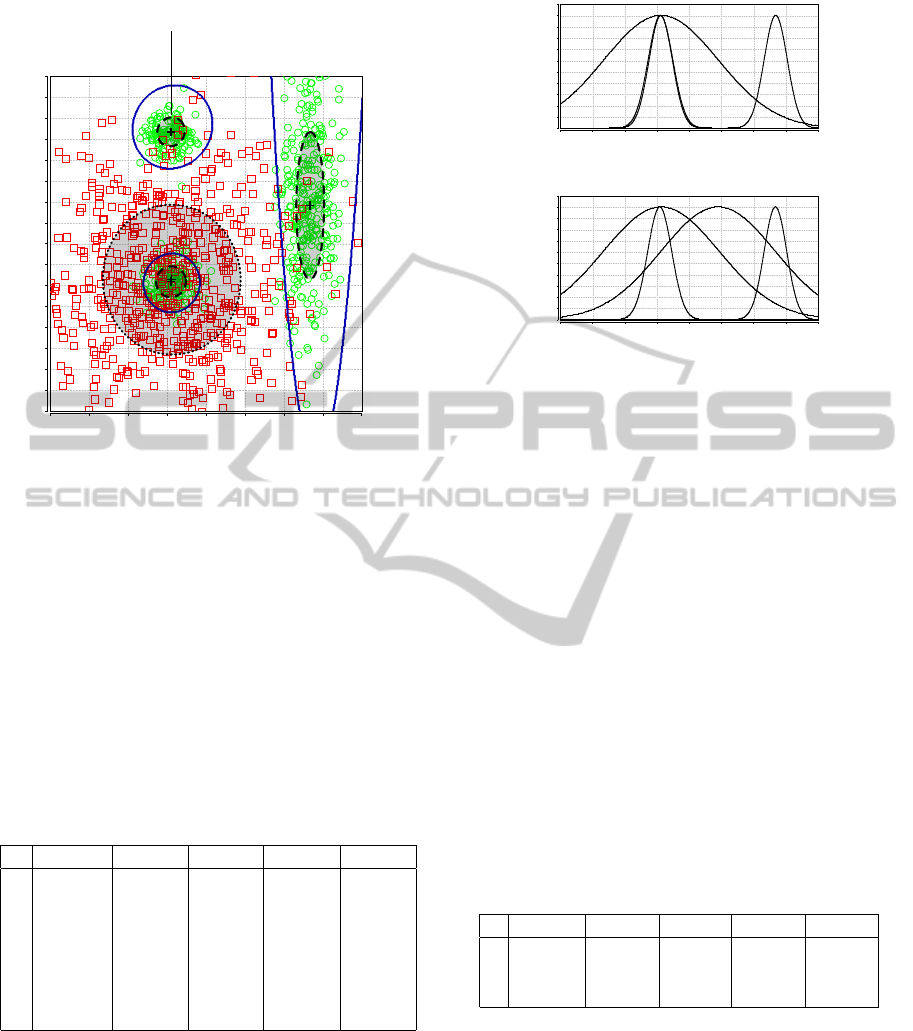
contains 5 000 samples belonging to two classes. Fig.

3 shows a part of the clouds samples together with

a classiﬁer trained on that data. There, the crosses

(+) describe the centers of the Gaussian components

of the trained GMM, the ellipses are corresponding

level curves (surfaces of constant density with a Ma-

halanobis distance of one to the corresponding cen-

ter) with shapes deﬁned by their respective covariance

matrices. The solid blue line illustrates the decision

boundary of the classiﬁer. The VI algorithm was ini-

tialized with 15 components and it pruned the ﬁnal

GMM down to four. The model was trained with 75%

of the data set (i.e., 3 750 samples with a ﬁnal train-

ing error of 10.6%) and tested on the remaining 1 250

samples resulting in a classiﬁcation error of 9.9%.

Now, we assess this classiﬁer by means of our pro-

posed interestingness measures. Table 1 shows the

evaluation of the four components (i.e., rules) with re-

gard to uniqueness, informativeness, importance, dis-

crimination, and representativity. First, it can be seen

that the components 1 and 3 are distant to the re-

maining two components and, thus, their informative-

ness values are quite high. Additionally, they are only

slightly covered with samples of a different class (i.e.,

the red boxes) which leads to high uniqueness values.

Components 2 and 4, in contrast, belong to different

classes and overlap. Thus, their uniqueness and in-

formativeness values are lower. Note that they exhibit

identical informativeness because they are mutually

closest to each other and the informativeness measure

is symmetric. As the class of the red boxes is only

modeled by component 4, its inﬂuence on the deci-

sion boundary (i.e., its discrimination) is high. The

class of the green circles is modeled by the remaining

three components which results in lower discrimina-

tion values that scale with their importance (i.e., the

fraction of samples they cover). Representativity is

also highly correlated with importance as the more

samples are covered by a component the higher its in-

ﬂuence on the “goodness-of-ﬁt”.

Table 1: Evaluation of the Component-Based Measures for

the “Clouds” Data Set.

j uniq( j) info( j) imp( j) disc( j) repr( j)

1 0.903 0.889 0.498 0.460 0.141

2 0.657 0.771 0.246 0.133 0.048

3 0.908 0.922 0.256 0.210 0.085

4 0.853 0.771 0.667 0.803 0.234

Regarding the comprehensibility of the trained

classiﬁer it can be stated that the number of four com-

ponents is certainly very low which is a good basis for

a comprehensible classiﬁer. Counting the number of

different univariate Gaussians in every dimension re-

quires to determine the projections of the components

onto the axes corresponding to the different input di-

mensions. The unnormalized projections of the four

components on the x- and y-axes are shown in Fig. 4.

The projections on the x-axis, Fig. 4(a), show two

nearly identical univariate Gaussians centered at -0.5

whose Hellinger distance is below 0.01. Thus, they

are regarded as being identical from the viewpoint of

comprehensibility which results in 3 univariate Gaus-

sians in the x-dimension and 4 univariate Gaussians in

the y-dimension. An average of 3.5 rules per dimen-

sion is a very good value for a comprehensible classi-

ﬁer. The minimum distinguishability of 0.0, however,

deteriorates the comprehensibility. An example for

two components with this low distinguishability can

be seen for the y-axis projection, cf. Fig. 4(b), at the

intersection point (-0.5, 1).

4.2 “Iris” Data Set

The aim of the second case study is to investigate the

impact on classiﬁcation performance when the clas-

siﬁer is restricted to generate human-comprehensible

rules. For that purpose, we use the well-known “iris”

data set from the UCI machine learning repository

(Frank and Asuncion, 2010). This data set contains

three classes, each with 50 four-dimensional (all con-

tinuous) samples.

First, we train a classiﬁer without any restrictions,

i.e., with full covariance matrices. We run the VI al-

gorithm on the data set in a 4-fold cross-validation

(stratiﬁed data). With this parametrization, the result-

ing models consist of seven to ten components, de-

pending on the random initialization. The mean clas-

siﬁcation error on test data is 1.9% (std. dev. 1.1%).

Now, we evaluate the model of the last fold consisting

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

420

-2,0 -1,5 -1,0 -0,5 0,0 0,5 1,0 1,5 2,0

-2,00

-1,75

-1,50

-1,25

-1,00

-0,75

-0,50

-0,25

0,00

0,25

0,50

0,75

1,00

1,25

1,50

1,75

2,00

Component 1





Component 2





Component 3

Component 4

Figure 3: CMM for the “Clouds” Data Set.

of seven components with our interestingness mea-

sures, cf. Tab. 2. The uniqueness and informativeness

measures show that all components are very “tight”

around their underlying samples and all components

are very well localized (i.e., almost no overlap). The

importance measure clearly shows four components

that cover a large portion of samples. Interestingly,

one of them has almost no impact on the decision

boundary, as shown by the discrimination measure.

As we have already stated in the ﬁrst case study, rep-

resentativity is highly correlated with importance.

Table 2: Evaluation of the Component-Based Measures for

the Classiﬁer with Seven Components and Full Covariance

Matrices.

j uniq( j) info( j) imp( j) disc( j) repr( j)

0 1.000 1.000 0.611 1.000 0.180

1 0.944 0.913 0.544 0.359 0.052

2 1.000 0.936 0.404 0.026 0.027

3 1.000 0.994 0.062 0.000 0.005

4 0.931 0.913 0.537 0.282 0.027

5 1.000 0.981 0.254 0.000 0.017

6 1.000 0.937 0.126 0.026 0.007

Regarding the classiﬁcation performance it can be

seen that the VI algorithm is able to generate very

good classiﬁers for this data set. However, from the

viewpoint of a data miner who wants to extract inter-

esting rules, our evaluation reveals that the classiﬁer

is too detailed and even models regions in the input

space that contain very little information.

Thus, we parametrize the VI algorithm to seek a

solution with a lower number of components which

-2,0 -1,5 -1,0 -0,5 0,0 0,5 1,0 1,5 2,0

0,0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

1,1

(a) x-Axis

-2,0 -1,5 -1,0 -0,5 0,0 0,5 1,0 1,5 2,0

0,0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

1,1

(b) y-Axis

Figure 4: Projection of the Gaussians onto the x- and y-Axes

for the “Clouds” Data Set.

usually results in a less detailed model. Again, we

perform a 4-fold cross-valiation which results in a

mean test error of 3.8% (std. dev. 3.8%). This time,

all four generated classiﬁers consist of three compo-

nents (one for each class). The results of our interest-

ingness measures for the classiﬁer of the last fold are

listed in Tab. 3. Uniqueness and informativenes show

that one class is well separated from the remaining

two classes. The last two classes (and the respective

components) overlap to a certain degree. As every

class in this coarse-grained model is modeled with a

single component, importance shows identical values

for all components. The overlap of the classes is also

reﬂected by discrimination and representativity since

the well-separated component has a larger value than

the remaining two components.

Table 3: Evaluation of the Component-Based Measures for

the Classiﬁer with Three Components and Full Covariance

Matrices.

j uniq( j) info( j) imp( j) disc( j) repr( j)

0 1.000 0.993 0.500 1.000 0.027

1 0.829 0.677 0.500 0.795 0.014

2 0.856 0.677 0.500 0.795 0.007

This result is a very good starting point to ﬁnd a

comprehensible classiﬁer. Now, we restrict the VI

algorithm to diagonal covariance matrices to enable

the extraction of human-comprehensible classiﬁca-

tion rules. In a 4-fold cross-validation all models con-

sist of three components again and yield a mean test

error of 4.5% (Std. dev. 3.3%). Tab. 4 shows the as-

sessment of the classiﬁer of the last fold. Compared

to the classiﬁer with full covariance matrices unique-

ness and informativeness show similar values. Obvi-

IN YOUR INTEREST - Objective Interestingness Measures for a Generative Classifier

421

3.5 4.0 4.5 5.0 5.5 6.0 6.5 7.0 7.5 8.0 8.5 9.0 9.5

0.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.0

(a) 1st Dimension

1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0

0.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.0

(b) 2nd Dimension

0 1 2 3 4 5 6 7 8

0.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.0

-1.0 -0.5 0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5

0.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.0

(d) 4th Dimension

Figure 5: Projections of the Classiﬁer with Three Components and Diagonal Covariance Matrices onto the Four Axes.

ously, the limited modeling capability of the classiﬁer

due to the restricted covariance matrices has no severe

impact for this data set.

Table 4: Evaluation of the Component-Based Measures for

the Classiﬁer with Three Components and Diagonal Covari-

ance Matrices.

j uniq( j) info( j) imp( j) disc( j) repr( j)

0 1.000 0.995 0.500 1.000 0.028

1 0.815 0.739 0.500 0.718 0.014

2 0.857 0.739 0.500 0.718 0.005

Fig. 5 illustrates the projections of the three com-

ponents onto the four axes of the input space. From

the viewpoint of comprehensibility we can state that

the number of three components (i.e., three rules) is

certainly very good. The average number of terms per

dimension is also three since there are no two Gaus-

sians that should be regarded as being identical. How-

ever, the distinguishability is very low (i.e., 0.01193).

This is due to the projections of the second dimension,

cf. Fig. 5(b), where two of the three univariate Gaus-

sians are very close to each other and, thus, difﬁcult

to distinguish.

This case study showed that human-

comprehensible rules can be generated from a

classiﬁer if the VI algorithm is parametrized accord-

ingly. This comprehensibility, however, comes at the

cost of a reduced classiﬁcation performance as the

modeling capability of the classiﬁer is restricted. A

compromise between understandability and classiﬁ-

cation performance is to only reduce the number of

components while still allowing full covariance ma-

trices. Then, our proposed interestingness measures

enable a higher-level analysis of the structure of the

data.

4.3 “Heart” Data Set

Some of the proposed interestingness measures can

be used to automatically prune components from

a trained classiﬁer. We demonstrate this with the

“heart” data set from the UCI machine learning

repository (Frank and Asuncion, 2010). This 12-

dimensional data set (six continuous and six categor-

ical dimensions) consists of 270 samples which are

partitioned into two classes. A 4-fold cross-validation

of the VI algorithm results in a mean test error of

29.13%.

We select the model from the last fold which

consists of 20 components and yields a test error of

25.0%. Then, we reduce the size of this classiﬁer by

pruning all components whose discrimination mea-

sure is below 0.1. The mixture coefﬁcients of the

remaining components are renormalized. The result-

ing classiﬁer consists of only two components (which

corresponds to a size reduction of 90%) and still

achieves the same test error of 25.0% (i.e., all pruned

components had a discrimination value of 0.0).

While the reduction of the original model is cer-

tainly optimal from the viewpoint of classiﬁcation

performance, it does not model the structure of the

data anymore and, thus, is not suitable for data anal-

ysis. Therefore, we used again the classiﬁer from the

last fold with 20 components as a starting point and

pruned all components with a discrimination below

0.1 and an importance below 0.1 (i.e., components

that only cover a few data points are deleted). The

resulting model has seven components and still yields

a test error of 25.0%. This is optimal regarding the

classiﬁcation performance and the interesting regions

in the input space are modeled.

Tab. 5 summarizes the results of this case study.

Certainly, it is possible to use even more interest-

ingness measures for a more sophisticated classiﬁer

pruning. Depending on the kind of rules the data

miner is interested in, informativeness (rules that are

distant to the remaining rules, cf. exception min-

ing) or uniqueness (rules representing unambiguous

knowledge) can be used additionally.

Table 5: Pruning results.

Pruning Size Test error

none (original model) 20 25.0%

disc ≤ 0.1 2 25.0%

disc ≤ 0.1 and impo ≤ 0.1 7 25.0%

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

422

5 CONCLUSIONS

AND OUTLOOK

In this article, we ﬁrst presented a probabilistic clas-

siﬁer based on mixture models (CMM) that can be

used in the ﬁeld of data mining to extract classiﬁca-

tion rules from labeled sample data. Then, we deﬁned

some objective interestingness measures that are tai-

lored to measure various aspects of the rules of which

this classiﬁer consists. These measures are also based

on probabilistic methods. A data miner may use these

measures to investigate the knowledge extracted from

sample data in more detail. In three case studies using

well-known data sets we demonstrated the application

of our approach.

In our future work we will investigate the pos-

sibility to apply our objective measures to each of

the C class-speciﬁc mixture models to obtain an even

more detailed class-speciﬁc assessment of the compo-

nents. In this work we used the measures as a post-

processing step to prune a trained model. However,

it is also possible to use them as side conditions in

the objective functions that are used for the training

of CMM in order to support certain properties of a

classiﬁer already during training. Additionally, we

will investigate how the measures can be combined

to perform a ranking of rules based on their interest-

ingness. There is a close relation of CMM to certain

kinds of fuzzy classiﬁers concerning the functional

form as outlined in (Fisch et al., 2010). Thus, it would

also be interesting to transfer the proposed measures

to that kind of classiﬁers and compare them to other

measures.

REFERENCES

Atzmueller, M., Baumeister, J., and Puppe, F. (2004).

Rough-fuzzy MLP: modular evolution, rule genera-

tion, and evaluation. In 15th International Conference

of Declarative Programming and Knowledge Man-

agement (INAP-2004), pages 203–213, Potsdam, Ger-

many.

Basu, S., Mooney, R. J., Pasupuleti, K. V., and Ghosh, J.

(2001). Evaluating the novelty of text-mined rules us-

ing lexical knowledge. In Proceedings of the seventh

ACM SIGKDD International Conference on Knowl-

edge Discovery and Data Mining (KDD 2001), pages

233–238, San Francisco, CA.

Bishop, C. (1994). Novelty detection and neural network

validation. IEE Proceedings – Vision, Image, and Sig-

nal Processing, 141(4):217–222.

Bishop, C. M. (2006). Pattern Recognition and Machine

Learning. Springer, New York, NY.

Di Fiore, F. (2002). Visualizing interestingness. In Zanasi,

A., Brebbia, C., Ebecken, N., and Melli, P., editors,

Data Mining III. WIT Press, Southampton, U.K.

Duda, R. O., Hart, P. E., and Stork, D. G. (2001). Pattern

Classiﬁcation. John Wiley & Sons, Chichester, New

York, NY.

Fayyad, U. M., Piatetsky-Shapiro, G., and Smyth, P. (1996).

Knowledge discovery and data mining: Towards a

unifying framework. In Proceedings of the Second In-

ternational Conference on Knowledge Discovery and

Data Mining (KDD 1996), pages 82–88, Portland,

OR.

Fisch, D., K

uhbeck, B., Ovaska, S. J., and Sick, B. (2010).

So near and yet so far: New insight into properties of

some well-known classiﬁer paradigms. Information

Sciences, 180:3381–3401.

Fisch, D. and Sick, B. (2009). Training of radial ba-

sis function classiﬁers with resilient propagation and

variational Bayesian inference. In Proceedings of the

International Joint Conference on Neural Networks

(IJCNN ’09), pages 838–847, Atlanta, GA.

Frank, A. and Asuncion, A. (2010). UCI machine learning

repository.

Hebert, C. and Cremilleux, B. (2007). A uniﬁed view of

objective interestingness measures. In Perner, P., ed-

itor, Machine Learning and Data Mining in Pattern

Recognition, number 4571 in LNAI, pages 533–547.

Springer, Berlin, Heidelberg, Germany.

Hilderman, R. J. and Hamilton, H. J. (2001). Knowledge

Discovery and Measures of Interest. Kluwer Aca-

demic Publishers, Norwell, MA.

Liu, B., Hsu, W., Chen, S., and Ma, Y. (2000). Analyz-

ing the subjective interestingness of association rules.

IEEE Intelligent Systems, 15(5):47–55.

McGarry, K. (2005). A survey of interestingness measures

for knowledge discovery. The Knowledge Engineer-

ing Review, 20(1):39–61.

Nauck, D. D. (2003). Measuring interpretability in rule-

based classiﬁcation systems. In Proceedings of the

12th IEEE International Conference on Fuzzy Sys-

tems (FUZZ-IEEE’03), volume 1, pages 196–201, St.

Louis, MO.

Padmanabhan, B. and Tuzhilin, A. (1999). Unexpectedness

as a measure of interestingness in knowledge discov-

ery. Decision Support Systems, 27(3):303–318.

Piatetsky-Shapiro, G. and Matheus, C. (1994). The inter-

estingness of deviations. In Proceedings of the AAAI-

94 Workshop on Knowledge Discovery in Databases

(KDD 1994), pages 25–36, Seattle, WA.

Silberschatz, A. and Tuzhilin, A. (1996). What makes

patterns interesting in knowledge discovery systems.

IEEE Transactions on Knowledge And Data Engi-

neering, 8:970–974.

Taha, I. and Ghosh, J. (1997). Evaluation and ordering of

rules extracted from feedforward networks. In Inter-

national Conference on Neural Networks, volume 1,

pages 408–413, Houston, TX.

Tan, P.-N., Kumar, V., and Srivastava, J. (2004). Selecting

the right objective measure for association analysis.

Information Systems, 29(4):293–313.

UCL (2007). Elena Database. http://www.ucl.ac.be/mlg/

index.php?page=Elena.

IN YOUR INTEREST - Objective Interestingness Measures for a Generative Classifier

423