PROBABILISTIC PLAN RECOGNITION FOR INTELLIGENT

INFORMATION AGENTS

Towards Proactive Software Assistant Agents

Jean Oh, Felipe Meneguzzi and Katia Sycara

Robotics Institute, Carnegie Mellon University, Pittsburgh, PA, U.S.A.

Keywords:

Proactive assistant agents, Probabilistic plan recognition, Information agents, Agent architecture.

Abstract:

In this paper, we present a software assistant agent that can proactively manage information on behalf of cog-

nitively overloaded users. We develop an agent architecture, known here as ANTicipatory Information and

Planning Agent (ANTIPA), to provide the user with relevant information in a timely manner. In order both to

recognize user plans unobtrusively and to reason about time constraints, ANTIPA integrates probabilistic plan

recognition with constraint-based information gathering. This paper focuses on our probabilistic plan predic-

tion algorithm inspired by a decision theory that human users make decisions based on long-term outcomes.

A proof of concept user study shows a promising result.

1 INTRODUCTION

When humans engage in complex activities that chal-

lenge their cognitive skills and divide their attention

among multiple competing tasks, the quality of their

task performance generally degrades. Consider, for

example, an operator (or a user) at an emergency cen-

ter who needs to coordinate rescue teams for two si-

multaneous ﬁres within her jurisdiction. The user

needs to collect the current local information regard-

ing each ﬁre incident in order to make adequate de-

cisions concurrently. Due to the amount of informa-

tion needed and the constraints that the decisions must

be made urgently the user can be cognitively over-

loaded, resulting in low quality decisions. In order

to assist cognitively overloaded users, research on in-

telligent software agents has been vigorous, as illus-

trated by numerous recent projects (Chalupsky et al.,

2002; Freed et al., 2008; Yorke-Smith et al., 2009).

In this paper, we present an agent architecture

known here as ANTicipatory Information and Plan-

ning Agent (ANTIPA) that can recognize the user’s

high-level goals (and the plans towards those goals)

and prefetch information relevant to the user’s plan-

ning context, allowing the user to focus on problem

solving. In contrast to a reactive approach to assis-

tance that uses certain cues to trigger assistive actions,

we aim to predict the user’s future plan in order to

proactively seek information ahead of time in antici-

pation of the users’s need, offsetting possible delays

and unreliability of distributed information.

In particular, we focus on our probabilistic plan

recognition algorithm following a decision-theoretic

assumption that the user tries to reach more valuable

world states (goals). Speciﬁcally, we utilize a Markov

Decision Processes (MDP) to predict a stochastic user

behavior, i.e.,the better the consequence of an action

is, the more likely the user takes the action. We ﬁrst

present the algorithm for a fully observable setting,

and then generalize the algorithm for partially observ-

able environments where the assistant agent may not

be able to fully observe the user’s current states and

actions.

The main contributions of this paper are as fol-

lows. We present the ANTIPA architecture that en-

ables the agent to perform proactive information man-

agement by seamlessly integrating information gath-

ering with plan recognition. In order to accommo-

date the user’s changing needs, the agent continuously

updates its prediction of the user plan and adjusts

its information-gathering plan accordingly. Among

the components of the ANTIPA architecture, this pa-

per is focused on describing our probabilistic plan

recognition algorithm for predicting the user’s time-

constrained needs for assistance. For a proof of con-

cept evaluation, we design and implement an abstract

281

Oh J., Meneguzzi F. and Sycara K..

PROBABILISTIC PLAN RECOGNITION FOR INTELLIGENT INFORMATION AGENTS - Towards Proactive Software Assistant Agents.

DOI: 10.5220/0003187102810287

In Proceedings of the 3rd International Conference on Agents and Artiﬁcial Intelligence (ICAART-2011), pages 281-287

ISBN: 978-989-8425-41-6

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

game that is simple yet conveys the core characteris-

tics of information-dependent planning problem, and

report promising preliminary user study results.

2 RELATED WORK

Plan recognition refers to the task of identifying a

user’s high-level goals (or intentions) by observing

the user’s current activities (Armentano and Amandi,

2007). The majority of existing work in plan recog-

nition relies on a plan library that represents a set of

alternative ways to solve a domain-speciﬁc problem,

and aims to ﬁnd a plan in the library that best explains

the observed behavior. In order to avoid the cumber-

some process of constructing elaborate plan libraries

of all possible plan alternatives, recent work proposed

the idea of formulating plan recognition as a plan-

ning problem using classical planners (Ram

ırez and

Geffner, 2009) or decision-theoretic planners (Baker

et al., 2009). In this paper, we develop a plan recog-

nition algorithm using a decision-theoretic planner.

A Markov Decision Process (MDP) is a rich

decision-theoretic model that can concisely represent

various real-life decision-making problems (Bellman,

1957). In cognitive science, MDP-based cognition

models have been proposed to represent computation-

ally how people predict the behavior of other (ratio-

nal) agents (Baker et al., 2009). Based on the as-

sumption that the observed actor tries to achieve some

goals, human observers predict that the actor would

act optimally towards the goals; the MDP-based mod-

els were shown to reﬂect such human observers’ pre-

dictions. In this paper, we use an MDP model to de-

sign a software assistant agent to recognize user be-

havior. In this regard, we can say that our algorithm

is similar to how human assistants would predict the

user’s behavior.

A Partially Observable MDP (POMDP) approach

was used in (Boger et al., 2005) to assist demen-

tia patients, where the agent learns an optimal pol-

icy to take a single best assistive action in the current

context. In contrast, ANTIPA separates plan recogni-

tion from the agent’s action selection (e.g.,gathering

or presenting information), which allows the agent

to plan and execute multiple alternative information-

gathering (or information-presenting) actions, while

reasoning about time constraints.

3 THE ANTIPA ARCHITECTURE

In order to address the challenges of proactive infor-

mation assistance, we have designed the ANTIPA ar-

chitecture (Oh et al., 2010) around four major mod-

ules: observation, cognition, assistance, and interac-

tion as illustrated in Figure 1.

Plan

recognition

Workload

estimation

Cognition

Information

management

Policy

management

Assistance

Keyboard

…

Feedback

…

Observation

negotiate

retrieve

Info. presenter

…

Warning alert

Interaction

Predicted

user plan

Figure 1: The ANTIPA agent architecture.

Observation Module receives various inputs from

the user’s computing environment, and translates

them into observations suitable for the cognition mod-

ule. Here, the types of observations include the key-

board and mouse inputs or the user feedback on the

agent assistance.

Cognition Module uses the observations received

from the observation module to model the user be-

havior. For instance, the plan recognition submod-

ule continuously interpret the observations to recog-

nize the user’s plans for current and future activities.

At the same time, in order to prevent overloading the

user with too much information, the workload estima-

tion submodule is responsible for assessing the user’s

current mental workload. Here, workload can be es-

timated using various observable metrics such as the

user’s job processing time to determine the level of

assistance that the user needs.

Assistance Module is responsible for deciding the ac-

tual actions that the agent can perform to assist the

user. For instance, given a predicted user plan, an

information management module can prefetch spe-

ciﬁc information needed in the predicted user plan,

while the policy management module can verify the

predicted plan according to the policies that the user

must abide by. Our focus here is on information

management. In order to manage information efﬁ-

ciently, we construct an information-gathering plan

that must consider the tradeoff between obtaining

the high-priority information (which is most relevant

to user plan) and satisfying temporal deadline con-

straints (indicating that information must be obtained

before the actual time when the user needs it).

Interaction Module decides when to offer certain in-

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

282

formation to the user based on its belief about the rel-

evance of information to the user’s current state, as

well as the format of information that is aligned with

the user’s cognitive workload. In order to accomplish

this task, the interaction module receives retrieved in-

formation from the information management module,

and determines the timing for information presenta-

tion based on the user mental workload assessed by

the cognition module.

Note that the focus this paper is on the plan recog-

nition module to identify the user’s current plan and

predict its future steps. Thus, we shall not go into

further detail about the other modules, except where

necessary for the understanding of plan recognition.

4 PLAN RECOGNITION

Based on the assumption that a human user intends

to act rationally, we use a decision-theoretic model

to represent a human user’s reasoning about conse-

quences to maximize her long-term rewards. We ﬁrst

assume that the agent can fully observe the user’s cur-

rent state and action, and knows the user’s starting

state. These assumptions will later be relaxed as de-

scribed in Section 4.4.

4.1 MDP-based User Model

We take a Markov Decision Process (MDP) to repre-

sent the user’s planning process. An MDP is a state-

based model of a sequential (discrete time) decision-

making process for a fully observable environment

with a stochastic transition model, i.e.,there is no un-

certainty regarding the user’s current state, but transi-

tioning from one state to another is nondeterministic

(Bellman, 1957). The user’s objective, modeled in an

MDP, is to create a plan that maximizes her long-term

cumulative reward.

Formally, an MDP is represented as a tuple

hS, A, r, T, γi where S denotes a set of states; A, a set of

actions; r : S ×A → R, a function specifying a reward

(from an environment) of taking an action in a state;

T : S ×A × S → R, a state transition function; and γ, a

discount factor indicating that a reward received in the

future is worth less than an immediate reward. Solv-

ing an MDP generally refers to a search for a policy

that maps each state to an optimal action with respect

to a discounted long-term expected reward.

4.2 Goal Recognition

The ﬁrst part of our algorithm recognizes the user’s

current goals from a set of candidate goals (or re-

Algorithm 1: An algorithm for plan recognition.

1: function PREDICT-USER-PLAN (MDP Φ, goals

G, observations O)

2: t ← Tree()

3: n ← Node()

4: addNodeToTree(n,t)

5: current-state s ← getLastObservation(O)

6: for all goal g ∈ G do

7: π

← valueIteration(Φ, g)

8: w

← Equation (1)

9: BLD-PLAN-TREE(t, n, π

, s, w

, 0)

warding states) from an observed trajectory of user

actions. We deﬁne set G of possible goal states as

all states with positive rewards such that G ⊆ S and

r(g) > 0, ∀g ∈ G.

Initialization. The algorithm initializes the proba-

bility distribution over the set G of possible goals,

denoted by p(g) for each goal g in G, proportion-

ally to the reward r(g): such that

∑

g∈G

p(g) = 1 and

p(g) ∝ r(g). The algorithm then computes an optimal

policy π

for each goal g in G, considering a positive

reward only from the speciﬁed goal state g and zero

rewards from any other states s ∈ S ∧ s 6= g. We use

a variation of the value iteration algorithm (Bellman,

1957) for solving an MDP (line 7 of Algorithm 1).

Goal Estimation. Let O

= s

, a

, s

, a

, ..., s

, a

de-

note a sequence of observed states and actions from

time steps 1 through t where s

∈ S, a

∈ A, ∀t

∈

{1, ...,t}. Here, the assistant agent needs to estimate

the user’s targeted goals.

After observing a sequence of user states and ac-

tions, the assistant agent updates the conditional prob-

ability p(g|O

) of that the user is pursuing goal g

given the sequence of observations O

. The condi-

tional probability p(g|O

) can be rewritten using the

Bayes rule as:

p(g|O

) =

p(s

, a

, ..., s

, a

|g)p(g)

∑

∈G

p(s

, a

, ..., s

, a

)p(g

)

.(1)

By applying the chain rule, we can write the condi-

tional probability of observing the sequence of states

and actions given a goal as:

p(s

, a

, ...,s

, a

|g) = p(s

|g)p(a

, g)p(s

, a

, g)

... p(s

t−1

, a

t−1

, ...,s

, g).

By the MDP problem deﬁnition, the state transi-

tion probability is independent of the goals. By the

Markov assumption, the state transition probability is

also independent of any past states except the current

state, and the user’s action selection depends only on

PROBABILISTIC PLAN RECOGNITION FOR INTELLIGENT INFORMATION AGENTS - Towards Proactive

Software Assistant Agents

283

the current state and the speciﬁc goal. Using these

conditional independence relationships, we get:

p(s

, a

, ..., s

, a

|g) = p(s

)p(a

, g)p(s

, a

)

... p(s

t−1

, a

t−1

), (2)

where the probability p(a|s, g) represents the user’s

stochastic policy π

(s, a) for selecting action a from

state s given goal g that has been computed at the ini-

tialization step.

By combining Equation 1 and 2, the conditional

probability of a goal given a series of observations can

be obtained. We use this conditional probability to

assign weights when constructing a tree of predicted

plan steps. That is, a set of likely plan steps towards a

goal is weighted by the conditional probability of the

user pursuing the goal.

Handling Changing Goals. The user may change

a goal during execution, or the user may interleave

plans for multiple goals at the same time. Our al-

gorithm for handling changing goals is to discount

the values of old observations as follows. The like-

lihood of a sequence of observations given a goal

is expressed in a product form such that p(O

|g) =

p(o

t−1

, g) × ... × p(o

, g) × p(o

|g). In or-

der to discount the mass from each observation

p(o

t−1

, g) separately, we ﬁrst take the logarithm

to transform the equation to a sum of products, and

then discount each term as follows:

log[p(O

|g)] = γ

log[p(o

t−1

, g)] +

... +γ

t−1

log[p(o

|g)],

where γ is a discount factor such that the most re-

cent observation is not discounted and the older ob-

servations are discounted exponentially. Since we are

only interested in relative likelihood of observing the

given sequence of states and actions given a goal,

such a monotonic transformation is valid (although

this value no longer represents a probability).

4.3 Plan Prediction

The second half of the algorithm is designed to pre-

dict the most likely sequence of actions that the user

will take in the future. Here, we describe an algo-

rithm for predicting plan steps for one goal. Using

the goal weights that have been computed earlier us-

ing Equation 1, the algorithm combines the predicted

plan steps for all goals as shown in Algorithm 1.

Initialization. The algorithm computes an optimal

stochastic policy π for the MDP problem with one

speciﬁc goal state. This policy can be computed by

solving the MDP to maximize the long-term expected

Algorithm 2: Recursive building of a plan tree.

function BLD-PLAN-TREE(plan-tree t, node n, policy

π, state s, weight w, deadline d)

for all action a ∈ A do

← π(s, a)w

if w

> threshold θ then

← Node(action a, priority w

, deadline d)

add new child node n

to node n

← sampleNextState(state s, action a)

BLD-PLAN-TREE(t, n

, π, s

, w

, d + 1)

rewards. Instead of a deterministic policy that spec-

iﬁes only the best action that results in the maxi-

mum reward, we compute a stochastic policy such

that probability p(a|s, g) of taking action a given state

a when pursuing goal g is proportional to its long-

term expected value v(s, a, g):

p(a|s, g) ∝ β v(s, a, g),

where β is a normalizing constant. The intuition for

using a stochastic policy is to allow the agent to ex-

plore multiple likely plan paths in parallel, relaxing

the assumption that the user always acts to maximize

her expected reward.

Plan-tree Construction. From the last observed user

state, the algorithm constructs the most likely future

plans from that state. Thus, the resulting output is a

tree-like plan segment, known here as a plan-tree, in

which a node contains a predicted user-action asso-

ciated with the following two features: priority and

deadline. We compute the priority of a node from

the probability representing the agent’s belief that the

user will select the action in the future; that is, the

agent assigns higher priorities to assist those actions

that are more likely to be taken by the user. On the

other hand, the deadline indicates the predicted time

step when the user will execute the action; that is, the

agent must prepare assistance before the deadline by

which the user will need help.

The recursive process of predicting and construct-

ing a plan tree from a state is described in Algo-

rithm 2. The algorithm builds a plan-tree by travers-

ing the most likely actions (to be selected by the user)

from the current user state according to the policy

generated from the MDP user model. We create a new

node for an action if the policy prescribes a higher

probability to the action than some threshold θ; ac-

tions are pruned otherwise. After adding a new node,

the next state is sampled according to the stochastic

state transition of the MDP, and the routine is called

recursively for the sampled next state. The resulting

plan-tree represents a horizon of sampled actions for

which the agent can prepare appropriate assistance.

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

284

4 5

E S S

W S EE

Time step

4-1

4-5 5-8

8-11

4-3 3-6 6-7

7-8

Root

node

N: North

E: East

W: West

S: South

Information

needed for action S:

keycode to move

from room 8 to 11

1 2 3

Current position: 4

Destination: 11

5-…

pruned

0 1 2

3 4 5

6 7 8

Node for action S at

time step 3

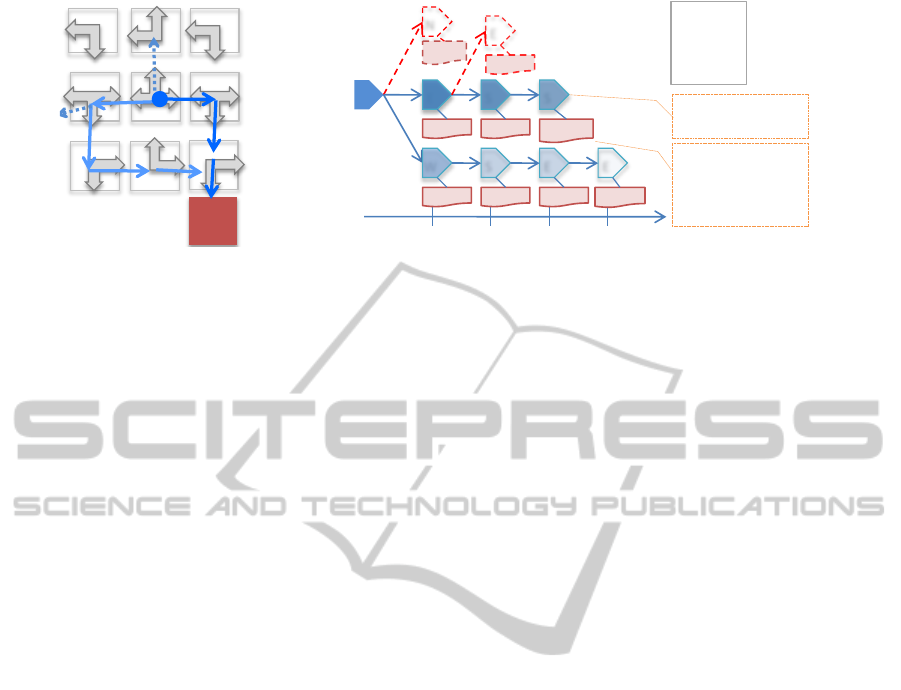
Figure 2: An example of a navigation problem (left) and a predicted user plan (right).

Illustrative Example. Figure 2 shows an example

where the user is navigating a grid to reach a destina-

tion (left). All available actions in a room are drawn

in boxed arrows. A stochastic state transition is omit-

ted here but we assume each action fails with some

probability, e.g.,the turning to the east action may fail,

resulting in the user’s current position unchanged. Let

us assume that the user needs information about a tar-

get location whenever making a move, e.g.,a key code

is required to move from one room to another. In

this problem, the agent generates a plan-tree of pos-

sible future user actions associated with relevant key

code information that the user will need for those ac-

tions (right). A node is shaded to reﬂect the predicted

probability of the user taking the associated action

(i.e.,the darker, the more likely), and the time step

represents the time constraint of information gather-

ing. The predicted plan (right) thus illustrates alterna-

tive plan steps towards the destination, putting more

priorities on shorter routes.

4.4 Handling Partial Observability

Hitherto we have described algorithms based on the

agent’s full observability on user states. We extend

our approach to handle a partially observable model

for the case when the assistant agent cannot directly

observe the user states and actions. Instead of observ-

ing the user’s states and actions directly, the agent

maintains a probability distribution over the set of

user states, known as a belief state, that represents

the agent’s belief regarding the user’s current state

inferred from indirect observations such as keyboard

and mouse inputs from the user’s computing environ-

ment or sensory inputs from various devices. For in-

stance, if no prior knowledge is available the initial

belief state can be a uniform distribution, indicating

that the agent believes that the user can be in any state.

The fully observable case can also be represented as

a special case of belief state where the whole proba-

bility mass is concentrated in one state. We use the

forward algorithm (Rabiner, 1989) to update a belief

state given a sequence of observations. We omit the

details due to space limitation.

5 EXPERIMENTS

As a proof of concept evaluation, we designed the

Open-Sesame game, that succinctly represents an

information-dependent planning problem. We note

that Open-Sesame is not meant to fully represent a

real-world scenario, but rather to evaluate the abil-

ity of ANTIPA to predict information needs in a con-

trolled environment.

The Open-sesame Game. The game consists of a

grid-like maze where the four sides of a room in the

grid can either be a wall or a door to an adjacent room;

the user must enter a speciﬁc key code to open each

door. Figure 2 (left) shows a simpliﬁed example. The

key codes are stored in a set of information sources;

a catalog of information sources speciﬁes which keys

are stored in each source as well as the statistical prop-

erties of the source. The user can search for a needed

key code using a browser-like interface. Here, de-

pending on the user’s planned path to the goal, the

user needs a different set of key codes. Thus, the key

codes to unlock the doors represent the user’s infor-

mation needs. In this context, the agent aims to pre-

dict the user’s future path and prefetch the key codes

that the user will need shortly.

Settings. We created three Open-Sesame games: one

6 × 6 and two 7 × 7 grids with varying degrees of dif-

ﬁculty. The key codes were distributed over 7 infor-

mation sources with varying source properties. The

only type of observations for the agent was the room

color which had been randomly selected from 7 col-

ors (here, we purposely limited the agent’s observa-

tion capability to simulate a partially observable set-

ting). The agent was given the map of a maze, the

user’s starting position, and the catalog of information

PROBABILISTIC PLAN RECOGNITION FOR INTELLIGENT INFORMATION AGENTS - Towards Proactive

Software Assistant Agents

285

Table 1: User study results for with (+) and without (−)

agent assistance.

−agent +agent

Total time (sec) 300 262.2

Total query time (sec) 48.1 10.7

Query time ratio 0.16 0.04

# of moves 13.2 14.6

# of steps away from goal 6.3 3

sources. During the experiments, each human subject

was given 5 minutes of time to solve a game either

with or without the agent assistance. In the experi-

ments, total 13 games were played by 7 subjects.

Results. The results are summarized in Table 1 that

compares the user performance on two conditions:

with and without agent assistance. In the table, the

total time measured the duration of a game; the game

ended when the subject either has reached the goal or

has used up the given time. The results indicate that

the subjects without agent assistance (−agent in Ta-

ble 1) were not able to reach a goal within the given

time, whereas the subjects with the agent assistance

(+agent) achieved a goal within the time limit in 6

out of 13 games. The total query time refers to the

time that a human subject has spent for information

gathering, averaged over all the subjects under the

same condition (i.e.,with or without agent assistance),

and the query time ratio represents how much time a

subject spent for information gathering relative to the

total time. The agent assistance reduced the user’s

information-gathering time to less than

In this experiment, we interpret the number of

moves that the user has made during the game (# of

moves) as the user’s search space in an effort to ﬁnd

a solution. On the other hand, the length of the short-

est path to the goal from the user’s ending state (# of

steps away from goal) can be considered as the qual-

ity of solution. The size of test subjects is too small

to draw a statistical conclusion. These initial results

are, however, promising since they indicate that intel-

ligent information management generally increased

the user’s search space and improved the user’s per-

formance with respect to the quality of solution.

6 CONCLUSIONS

The main contributions of this paper are the fol-

lowing. We presented an intelligent information

agent, ANTIPA, that anticipates the user’s informa-

tion needs using probabilistic plan recognition and

performs information gathering prioritized by the pre-

dicted user constraints. In contrast to reactive assis-

tive agent models, ANTIPA is designed to provide

proactive assistance by predicting the user’s time-

constrained information needs. The ANTIPA archi-

tecture allows the agent to reason about time con-

straints of its information-gathering actions; accom-

plishing equivalent behavior using a POMDP would

take an exponentially larger state space since the

state space must include the retrieval status of all in-

formation needs in the problem domain. We em-

pirically evaluated ANTIPA through a proof of con-

cept experiment in an information-intensive game set-

ting and showed promising preliminary results that

the proactive agent assistance signiﬁcantly reduced

the information-gathering time and enhanced the user

performance during the games.

In this paper, we have not considered the case

where the agent has to explore and learn about an

unknown (or previously incorrectly estimated) state

space. We made a speciﬁc assumption that the agent

knows the complete state space from which the user

may explore only some subset. In real-life scenarios,

users generally work in a dynamic environment where

they must constantly collect new information regard-

ing the changes in the environment, sharing resources

and information with other users. In order to address

such special issues that arise in the dynamic settings,

in our future work we will investigate techniques for

detecting environmental changes, incorporating new

information, and alerting the user of changes in the

environment.

ACKNOWLEDGEMENTS

This research was sponsored by the U.S. Army Re-

search Laboratory and the U.K. Ministry of De-

fence and was accomplished under Agreement Num-

ber W911NF-06-3-0001. The views and conclusions

contained in this document are those of the authors

and should not be interpreted as representing the ofﬁ-

cial policies, either expressed or implied, of the U.S.

Army Research Laboratory, the U.S. Government, the

U.K. Ministry of Defence or the U.K. Government.

The U.S. and U.K. Governments are authorized to re-

produce and distribute reprints for Government pur-

poses notwithstanding any copyright notation hereon.

REFERENCES

Armentano, M. G. and Amandi, A. (2007). Plan recognition

for interface agents. Artif. Intell. Rev., 28(2):131–162.

Baker, C., Saxe, R., and Tenenbaum, J. (2009). Action un-

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

286

derstanding as inverse planning. Cognition, 31:329–

349.

Bellman, R. (1957). A markov decision process. Journal of

Mathematical Mechanics, 6:679–684.

Boger, J., Poupart, P., Hoey, J., Boutilier, C., Fernie, G., and

Mihailidis, A. (2005). A decision-theoretic approach

to task assistance for persons with dementia. In Proc.

IJCAI, pages 1293–1299.

Chalupsky, H., Gil, Y., Knoblock, C., Lerman, K., Oh, J.,

Pynadath, D., Russ, T., and Tambe, M. (2002). Elec-

tric Elves: Agent technology for supporting human or-

ganizations. AI Magazine, 23(2):11.

Freed, M., Carbonell, J., Gordon, G., Hayes, J., Myers, B.,

Siewiorek, D., Smith, S., Steinfeld, A., and Tomasic,

A. (2008). Radar: A personal assistant that learns to

reduce email overload. In Proc. AAAI.

Oh, J., Meneguzzi, F., and Sycara, K. P. (2010). ANTIPA:

an architecture for intelligent information assistance.

In Proc. ECAI, pages 1055–1056. IOS Press.

Rabiner, L. (1989). A tutorial on HMM and selected

applications in speech recognition. Proc. of IEEE,

77(2):257–286.

Ram

ırez, M. and Geffner, H. (2009). Plan recognition as

planning. In Proc. IJCAI, pages 1778–1783.

Yorke-Smith, N., Saadati, S., Myers, K. L., and Morley,

D. N. (2009). Like an intuitive and courteous butler:

a proactive personal agent for task management. In

Proc. AAMAS, pages 337–344.

PROBABILISTIC PLAN RECOGNITION FOR INTELLIGENT INFORMATION AGENTS - Towards Proactive

Software Assistant Agents

287