INTEGRATED DYNAMICAL INTELLIGENCE FOR INTERACTIVE

EMBODIED AGENTS

Eric Aaron, Juan Pablo Mendoza

Department of Mathematics & Computer Science, Wesleyan University, Middletown, CT, U.S.A.

Henny Admoni

Department of Computer Science, Yale University, New Haven, CT, U.S.A.

Keywords:

Interactive embodied agents, Reactive intelligence, Hybrid reactive-deliberative agents, BDI agent modeling,

Hybrid dynamical systems.

Abstract:

For embodied agents that interact with people in time-sensitive applications, such as robot assistants or au-

tonomous characters in video games, effectiveness can depend on responsive and adaptive behavior in dynamic

environments. To support such behavior, agents’ cognitive and physical systems can be modeled in a single,

shared language of dynamical systems, an integrated design that supports performance with mechanisms not

readily available in other modeling approaches. In this paper, we discuss these general ideas and describe

how hybrid dynamical cognitive agents (HDCAs) employ such integrated modeling, resulting in dynamically

sensitive user interaction, task sequencing, and adaptive behavior. We also present results of the ﬁrst user-

interactive applications of HDCAs: As demonstrations of this integrated cognitive-physical intelligence, we

implemented our HDCAs as autonomous players in an interactive animated Tag game; resulting HDCA be-

havior included dynamic task re-sequencing, interesting and sensible unscripted behavior, and learning of a

multi-faceted user-speciﬁed strategy for improving game play.

1 INTRODUCTION

In interactiveapplications such as video games or per-

sonal robotics, embodied agents should be adaptive

and responsive to users. In this paper, we present an

intelligence modeling framework that supports these

qualities: Inﬂuenced by dynamicist cognitive science

—the study of mind as a dynamical system rather

than a discrete, computational one (Port and van

Gelder, 1995; Spivey, 2007)— our dynamical intel-

ligence model integrates the physical and cognitive

sub-systems of an agent in a shared language of dif-

ferential equations, providing a uniﬁed, dynamically

sensitive substrate for behavior. In particular, we de-

scribe how hybrid dynamical cognitive agents (HD-

CAs) (Aaron and Admoni, 2009; Aaron and Admoni,

2010) can reﬂect these ideas of integrated dynamical

intelligence, and to illustrate these ideas, we present

the ﬁrst user-interactive applications of HDCAs.

The design of HDCAs’ cognitive systems is inﬂu-

enced unconventionally by the belief-desire-intention

(BDI) theory of intention (Bratman, 1987) and its im-

plementations (e.g., (Georgeff and Lansky, 1987) and

successors), which established that BDI elements (be-

liefs, desires, intentions) are an effective foundation

for goal-directed intelligence. Unlike typical BDI

agents, HDCAs’ cognitive models interconnect BDI

elements in a continuously evolving system inspired

by spreading activation frameworks (Maes, 1989).

Each BDI element in an HDCA is represented by an

activation value, indicating its salience and intensity

“in mind” (e.g., intensity of commitment to an inten-

tion), and cognitive evolution is governed by differ-

ential equations, with activation values affecting rates

of change of other activations. HDCAs employ these

dynamical cognitive representations on both reactive

and deliberative levels, distributing goal-directed in-

telligence over both levels. For example, HDCAs can

re-order task sequences simply by evolution of dy-

namical intentions, without propositional deliberation

(Aaron and Admoni, 2009).

The physical systems of HDCAs —comprising

the elements pertinent for navigation, i.e., xy-location,

velocity, and heading angle— are also modeled by

differential equations; for this paper, HDCAs’ nav-

igation intelligence is based on (Goldenstein et al.,

296

Aaron E., Pablo Mendoza J. and Admoni H..

INTEGRATED DYNAMICAL INTELLIGENCE FOR INTERACTIVE EMBODIED AGENTS.

DOI: 10.5220/0003188102960301

In Proceedings of the 3rd International Conference on Agents and Artiﬁcial Intelligence (ICAART-2011), pages 296-301

ISBN: 978-989-8425-41-6

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

2001). Thus, physical and cognitive systems in HD-

CAs are uniﬁed in the common language of differen-

tial equations, which is critical to the HDCA learning

demonstrations in section 3.3.

Along with the continuous evolutions of cog-

nitive activations and physical variables, discrete

changes —e.g., transitions from one task or behavior

to another— can occur when activations reach pre-

speciﬁed thresholds. Thus, we formally model an

HDCA as a hybrid dynamical system (hybrid system,

for short) (Alur et al., 2000). Discrete task transitions

also illuminate the roles of intentions and sequencing

intentions (see section 2.1) in our HDCAs: Conceptu-

ally, sequencing intentions have activations that rep-

resent intentions to perform tasks in a temporal rela-

tionship (e.g., to perform X beforeY), as distinct from

standard intentions associated with individual tasks.

(In this paper, we consider only HDCAs with one

intention for each task.) Sequencing intentions are

critical elements of guards —threshold conditions for

when discrete transitions occur— in agents’ hybrid

systems, so dynamical task re-sequencing emerges or-

ganically from continuous cognition.

As a motivating example for the ideas in this pa-

per, consider a child playing Tag, avoiding a player

designated as It as well as other obstacles. She wants

to accomplish many things before the game ends: ac-

tively protect a friend in the game for a while; ac-

tively try to become It and tag an adversary; and

reach several bases, locations where she cannot be

tagged by It. She can only do one of these tasks at

a time, so she begins with an intended task sequence

that achieves her goals, but as the game proceeds, she

re-sequences tasks in response to her environment.

Moreover, while playing, her behavior shows sensi-

ble subtleties, such as making decisions a bit more

quickly when she’s comfortably near her goal.

In demonstrations for this paper, such a player is

implemented as an HDCA in an interactive, animated

Tag game, illuminating the capabilities of integrated

dynamical intelligence. In conventional agents, for

example, task re-sequencing such as the child per-

forms is deliberative, but in HDCAs, it arises from

sub-deliberative cognitive evolution. Moreover, our

integrated modeling enables moment-by-moment in-

teractions among elements considered cognitive and

those considered physical, which evoke micro-scale

effects that can cascade into observable effects (see

section 3.2). We also demonstrate how an HDCA can

learn a multi-faceted Tag strategy, perhaps based on

user input during a game, extending previous HDCA

learning methods to this application domain.

2 HYBRID DYNAMICAL

COGNITIVE AGENTS

HDCAs can be viewed as having physical and cogni-

tive sub-systems, composed of the differential equa-

tions and variables describing the behavior conven-

tionally considered physical or cognitive, respec-

tively; BDI elements are thus considered cognitive,

while xy-location and heading angle φ are physi-

cal. HDCAs are implemented by augmenting phys-

ical systems with cognitive BDI elements and their

activation values. For this paper, cognitive activa-

tions are within [−10, 10], where near-zero values in-

dicate low salience and greater magnitudes indicate

greater intensity of associated concepts—e.g., more

active intentions represent more commitment to the

related tasks. Negative values indicate salience of the

opposing concept, so, e.g., a moderate desire to not

cycle the bases and strong commitment to protect a

friend could be encoded by value −3 on a desire for

runBases

and value 9 on an intention for

protect

Our HDCAs’ cognitive activations are intercon-

nected in differential equations. A partial cognitive

system —with many equations omitted and terms

elided in equations shown— is in equation 1, in which

beliefs, desires, and intentions are represented by

variables beginning with b, d, and i, and time deriva-

tive variables are on the left in each equation:

dRun = −c

· bAmIt+ c

· iRun+ . . . (1)

iTag = d

· bAmIt− d

· dRun+ d

· iTag+ . . .

iRun = −e

· bAmIt− e

· dTag+ e

· iRun+ . . .

This illustrates interconnectedness: Elements have

excitatory or inhibitory inﬂuence on activations by in-

creasing or decreasing derivatives. In equation 1, vari-

ables stand for activations of cognitive elements such

as the desire to run around the bases (dRun) and the

belief that the agent is It (bAmIt); coefﬁcients repre-

sent the impacts of the connections between elements.

2.1 Our HDCA Implementation

Because HDCA behavior consists of switching

among multiple, continuous behaviors, our HDCA

implementation is based on a hybrid automaton (Alur

et al., 2000), a state-transition model of hybrid sys-

tems. Each hybrid automaton has discrete modes rep-

resenting individual behaviors or tasks, each having

differential equations that govern variables’ evolution

in that mode, and guard constraints describing when

mode transitions occur (see Figure 2). We straight-

forwardly implemented and simulated our HDCAs as

hybrid systems in MATLAB, with modes as functions

containing guards for mode transitions and dynamical

INTEGRATED DYNAMICAL INTELLIGENCE FOR INTERACTIVE EMBODIED AGENTS

297

systems for agent evolution. Within the hybrid au-

tomaton structure, our HDCAs also include the struc-

tures described below for dynamical intelligence.

2.1.1 Task Sequencing

In addition to standard intentions, our HDCAs have

sequencing intentions for dynamic task sequencing.

In this paper, we implement sequencing intentions as

pairs; the activation of sequencing intention (A, B) is

the difference in activations of corresponding inten-

tions, iA − iB, representing the commitment to per-

forming action A before action B. To determine task

sequence in an HDCA with actions α

. . . α

, for each

action α

, we sum activations on the k sequencing in-

tentions with α

in the ﬁrst position; the descending

order of these associated sums induces a sequence on

the actions. Sequencing intentions could in principle

encode other concepts, but this sufﬁces to illustrate

integrated intelligence in HDCAs.

Activations on intentions and sequencing inten-

tions evolve over time, so at any time, a new action α

might attain maximum priority and re-sequence tasks.

When a task is ﬁnished, intentions and sequencing in-

tentions are altered to reﬂect that, and the agent con-

tinues in the new maximal-priority action.

2.1.2 Cognitive-physical Integration

Because of integrated intelligence in HDCAs, any

variable, cognitive or physical, could affect any other

variable. To illustrate how any physical element in

HDCAs could subtly affect any aspect of cognitive

state, we demonstrate an extreme case: physical el-

ements considered “involuntary” affecting cognitive

elements considered “subconscious.” In particular,

we encode that cognitive dynamics, as speciﬁed by

differential equations governing activation evolutions,

should accelerate slightly when the agent is more “re-

laxed,” i.e., near a target location and not turning

rapidly. To do this, we construct a physical-cognitive

multiplier pcm so that physical values can affect ac-

tivations of BDI elements: values of pcm range from

1 to 1 + p, where p is a designer-speciﬁed parame-

ter, and intensify cognitive evolution by multiplica-

tion with time derivatives, e.g., iTag = pcm ·

iTag ·

timeStep+ . . ., instead of iTag =

iTag· timeStep+ . . ..

The pcm function in our demonstrations begins

with function e

−k

φ|+d)

of angular velocity

φ and cur-

rent distance d from the target, so that when (|

φ| + d)

is close to 0, the function value is close to 1, and as

φ| + d) gets larger, the function value gets closer to

0. Designer-chosen constant k

> 0 controls the rate

at which values approach 0 as (|

φ| + d) grows. Build-

ing upon this, to get our desired effect, we chose:

pcm = 1+ p



sin

−1

−k

φ|+d)

)



(2)

This enables a boost as agents near targets and

stop turning, with much less effect outside of the de-

sired range for (|

φ| + d); it could be changed for dif-

ferent effects. (Parameter values for our demonstra-

tions are available at (Aaron et al., 2011).)

3 EXPERIMENTS

As a demonstration domain for our HDCAs, we im-

plemented animated interactive Tag games containing

a user player and two kinds of autonomous players:

simple Tag agents, HDCAs with limited intelligence;

and cognitive Tag agents, with more extensive dy-

namical intelligence. Agents intuitively interact with

other agents and the user: Each It agent pursues some

non-It player; each non-It agent avoids It players and

views non-It players as safe. To make the game more

adversarial, agents also have slight anti-user biases,

and two players at a time are It. The ﬁeld of play

(Figure 1) is a square with bases near the corners,

obstacles between bases, and other players. Players

touching base cannot become It, but they cannot stay

on base too long before moving away. Players are pe-

nalized for touching an obstacle.

3.1 Autonomous Tag Players

A risk-averse non-It player could simply run clock-

wise from base to base, hoping not to be forced into

a position to get tagged. A simple Tag agent (STA)

executes that strategy. When an STA S becomes It,

it chooses from two possible It-actions: chasing the

user; or chasing an agent. If another It player is chas-

ing the user, S joins the chase; if not, S tries to tag

the closest non-It agent. In addition, if S engages

in one of these It-actions for a long time, “boredom”

sets in, represented by attenuation on the correspond-

ing intention activation, so S will eventually switch

to the other It-action. Unlike a cognitive Tag agent

(CTA), an STA’s cognitive structure is a very simple

dynamical intention-based system, straightforwardly

supporting only the design and behavior noted above.

A cognitive Tag agent more fully demonstrates

dynamical intelligence and cognitive-physical inte-

gration; see Figure 2 for its mode-level architecture

and BDI elements. When a CTA C is not It, it will

try to accomplish all of the following actions be-

fore the game ends:

runBases

, cycling the bases (as

STAs do);

getMitten

, retrieving its mitten (which

the poor agent drops in every game);

protect

, spend-

ing time protecting a friend from being tagged; and

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

298

2 3

Its: 7

Time: 2.0833

2 3

Its: 7

Time: 2.0833

2 3

Its: 7

Time: 2.0833

2 3

Its: 7

Time: 2.0833

2 3

Its: 7

Time: 2.0833

2 3

Its: 7

Time: 2.0833

2 3

Its: 7

Time: 2.0833

2 3

Its: 7

Time: 2.0833

2 3

Its: 7

Time: 2.0833

base

obstacle

human

-controlled

player

CTA

It STA

non-It

STA

base to

which CTA

is heading

Figure 1: An annotated screen shot of our Tag game, illustrating ﬁeld layout and players on the ﬁeld, including simple Tag

agents (STAs) and cognitive Tag agents (CTAs). Color variations distinguish entities, as does the convention that players,

human-controlled or automated, are numbered, while bases and obstacles are not. The program indicates the base to which

the cognitive Tag agent is heading by drawing a light circle around that base. See supplementary website (Aaron et al., 2011)

for further details of color, notation, and function of elements in our animated Tag games.

Figure 2: The mode-level architecture and BDI elements of a cognitive Tag agent. Each mode also has self-transitions, omitted

by convention to avoid visual clutter.

readyToTag

, trying to become It and tag an adver-

sary. The

getMitten

action is implemented by se-

lecting a time when, wherever C is, its mitten drops;

soon after, C ﬁnds the mitten’s location, and activa-

tions on BDI elements evolve until, in general, mitten-

retrieval becomes C’s highest priority. To enable

protect

and

readyToTag

, C has beliefs of afﬁnities

for each player in the game, and C will protect a non-

It player with maximal afﬁnity during

protect

, and

pursue a non-It player with minimal afﬁnity during

readyToTag

. These non-It actions are dynamically

re-sequenced, based on time pressure, afﬁnities, and

proximity to locations (e.g., a base, an adversary).

When a CTA is It, it either follows through on a

readyToTag

action or selects between pursuing the

user or an automated player, exactly as an STA would.

3.2 Experiments

We performed various demonstrations of HDCA in-

telligence. Some were proofs that our ideas work

as expected in sensible environments. One showed

that CTAs can follow instructions, e.g., that cogni-

tive evolution need not prevent them from completing

tasks in accord with initial intention activations. An-

other illustrated physical-cognitive multiplier pcm: In

a contrived situation, two cognitively identical CTAs

were equally near a target, one facing the target, the

other facing away; the CTAs then changed heading

angle as usual, but not position. As a result, the CTA

facing the target had higher pcm values and changed

task-modes faster than the other CTA. These are all

expected demonstrations of proper performance; for

more details, see (Aaron et al., 2011).

INTEGRATED DYNAMICAL INTELLIGENCE FOR INTERACTIVE EMBODIED AGENTS

299

In other experiments, speciﬁc values were var-

ied in controlled environments, to investigate partic-

ular effects. As examples, we simulated many game

segments with identical CTA C; initially, C’s inten-

tions implied task order [

readyToTag

runBases

protect

getMitten

]. Across simulations, two fac-

tors varied —when C dropped its mitten; and when

C was tagged by the user (which was automated,

for replicability)— to illuminate dynamicist effects in

game play. As mitten-drop grew later with get-tagged

held constant, for example, the time at whichC moved

from

readyToTag

into

runBases

was not affected,

but the time at which C then entered

protect

tended

to get earlier. In addition, for particular values of

mitten-drop and get-tagged, C entered

protect

mode

—in which movement is not obstacle-avoidant— at

an inopportune moment and ran straight into an It

player. This sequence of events and ensuing cascade

of effects illustrates how engaging, unscripted behav-

ior can emerge from the continuous-level variations

supported by our HDCA framework.

For additional details and other results, including

natural game play, see (Aaron et al., 2011).

3.3 Learning

To support learning from unpredictable users,

cognitive-physical integration is maximally ﬂexible:

All physical and cognitive variables can be intercon-

nected, and any connection can be modiﬁed by learn-

ing. For our demonstrations, HDCAs are trained by

reinforcement learning similar to that in (Aaron and

Admoni, 2010), which requires heuristics selecting

which connections to modify during learning and cri-

teria for when learning is complete. Learning occurs

without interrupting interactive applications.

As preparation, we ﬁrst determined control condi-

tion behavior by letting a game play extensively (for

more than 8000 simulated seconds), with an auto-

mated user for replicability. In this game setup, when

a cognitive Tag agent C

ctrl

became It, C

ctrl

would al-

most always tag some other player in less than 25 sim-

ulated seconds (average: 12.85 seconds). In addition,

the value a

ctrl

of the average number of bases reached

per execution of the

runBases

behavior, over the full

game, was a

ctrl

= 4.01 (see Figure 3).

Based on this, we demonstrated a CTA C learning

from a simulated user request to change one aspect

of game play without affecting another; it exempli-

ﬁes an arbitrary user choice, unrelated to agent de-

sign and substantivelychanging control behavior. The

goal had two components: speed change, requiring

speed-only learning; and base-running maintenance,

requiring speed-and-bases (SB) learning.

• Speed change: After becoming It, C should opti-

mally tag some other player between 25 and 45

seconds later. Speed-only training (and thus par-

tial SB training, see below) occurs when C tran-

sitions out of

chase

mode. If the time C was It

is outside of the desired range (25–45 seconds), C

is trained to become slower or faster, as appropri-

ate, by a factor that depends on exactly how far

outside of the desired range C was It.

• Base-running maintenance: Despite the effects

of speed-only learning, C should only minimally

change the value a

of the average number of

bases reached during each

runBases

behavior.

SB training occurs when C transitions out of

runBases

mode: a

is updated, and coefﬁcients

in cognitive differential equations are altered to

train C to approach the desired, control value

of 4.01 in the future. As a partial example, if

< 4.01, coefﬁcients in the differential equation

governing iRun are altered so that C tends to re-

main longer in

runBases

, encouraging greater a

in the future. The amounts altered depend on val-

ues such as the velocity ofC when training occurs,

exemplifying cognitive-physical integration: Val-

ues of physical variables affect cognitive adjust-

ments.

To focus our demonstrations, the connections mod-

iﬁed during training were pre-selected, though the

adjustments were autonomous. More details on the

learning process are available at supplementary web-

site (Aaron et al., 2011).

Our tests demonstrate C successfully learning

integrated cognitive-physical behavior during game

play: C slowed to spend more time as It before tag-

ging another player (average time: 32.62) while also

maintaining a bases average of a

= 4.21, very close

to 4.01. Figure 3 illustrates the effects of SB learning

on a

and base-running performance. Additionally,

Figure 3 shows that speed-only learning without full

SB learning resulted in a value of a

= 2.19 in other-

wise identical game play, suggesting the importance

of integrated learning for the desired goal.

4 CONCLUSIONS

This paper describes the integrated cognitive-physical

intelligence underlying our HDCAs, and it presents

the ﬁrst applications of HDCAs in interactive scenar-

ios. Agent cognition in our HDCAs is based on con-

tinuously evolving activations of BDI-based cognitive

elements, enabling a model that unites cognitive and

physical intelligences in a single system; as a result,

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

300

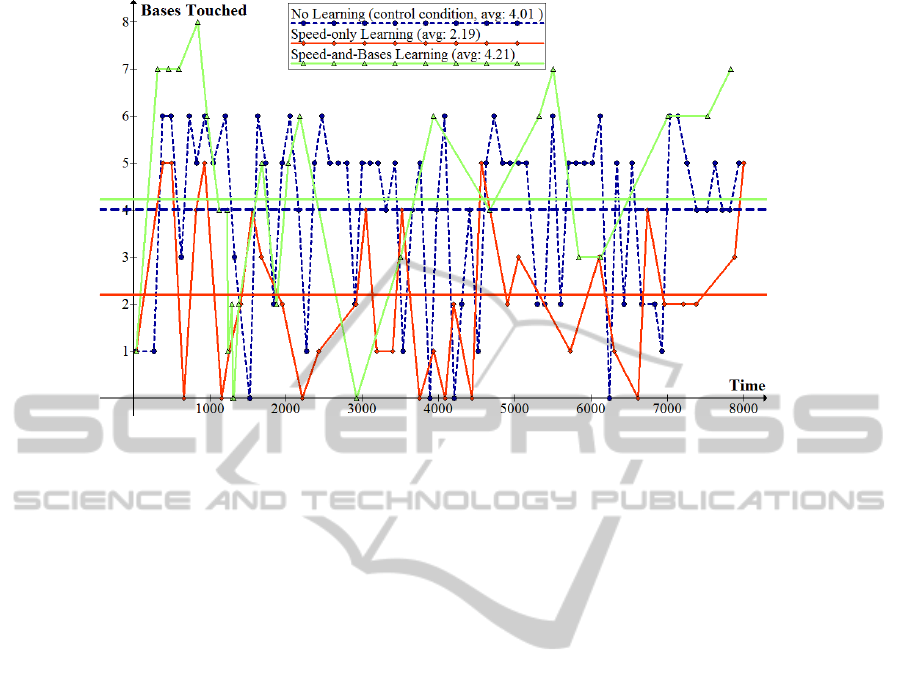
Figure 3: Results of learning. Lines correspond to the control condition agent (in dark blue, dotted line; circle data points), a

speed-only agent trained only to change its speed to meet criteria for time spent as It (mid-dark orange; diamond points), and

a speed-and-bases agent trained to both change its speed and change its cognitive system, to have a desired amount of time

spent as It and a

runBases

bases-average close to that in the control condition (light green line; triangle points).

HDCAs extend conventional reactivity without sacri-

ﬁcing real-time responsiveness. Demonstrations in an

animated Tag game suggest that integrated dynami-

cal intelligence supports reactive task sequencing and

sensible unscripted behavior that could improve game

play, and that HDCAs can exploit cognitive-physical

integration to learn multi-faceted strategies during

play. These examples illustrate general principles that

could apply to unpredictable learning requirements

during games or other interactive applications, for vir-

tual or physical agents.

ACKNOWLEDGEMENTS

The authors thank Jim Marshall, Tom Ellman, and

Michael Littman for their comments on previous ver-

sions of this paper, and the Wesleyan University

Hughes Program for funding support. The third au-

thor is supported by a National Science Foundation

Graduate Research Fellowship.

REFERENCES

Aaron, E. and Admoni, H. (2009). A framework for dynam-

ical intention in hybrid navigating agents. In Inter-

national Conference on Hybrid Artiﬁcial Intelligence

Systems, pages 18–25.

Aaron, E. and Admoni, H. (2010). Action selection and

task sequence learning for hybrid dynamical cog-

nitive agents. Robotics and Autonomous Systems,

58(9):1049–1056.

Aaron, E., Admoni, H., and Mendoza, J. (2011). Sup-

plementary website for this paper. Available at

http://eaaron.web.wesleyan.edu/icaart11supp.html.

Alur, R., Henzinger, T., Lafferriere, G., and Pappas, G.

(2000). Discrete abstractions of hybrid systems. Pro-

ceedings of the IEEE, 88(7):971–984.

Bratman, M. (1987). Intentions, Plans, and Practical Rea-

son. Harvard University Press, Cambridge, MA.

Georgeff, M. and Lansky, A. (1987). Reactive reasoning

and planning. In AAAI-87, pages 677–682.

Goldenstein, S., Karavelas, M., Metaxas, D., Guibas, L.,

Aaron, E., and Goswami, A. (2001). Scalable nonlin-

ear dynamical systems for agent steering and crowd

simulation. Computers And Graphics, 25(6):983–998.

Maes, P. (1989). The dynamics of action selection. In

IJCAI-89, pages 991–997.

Port, R. and van Gelder, T. (1995). Mind as Motion: Ex-

plorations in the Dynamics of Cognition. MIT Press,

Cambridge, MA.

Spivey, M. (2007). The Continuity of Mind. Oxford Univer-

sity Press, New York.

INTEGRATED DYNAMICAL INTELLIGENCE FOR INTERACTIVE EMBODIED AGENTS

301