THE IMPORTANCE OF TIES IN THE EFFICIENCY
OF CONVENTION EMERGENCE
Paulo Urbano, João Balsa, Paulo Ferreira and João Baptista
LabMAg, FCUL, Ed. C6, Piso 3, Campo Grande, 1749-016, Lisboa, Portugal
Keywords: Convention emergence, Collective choice, Multi-agent systems coordination.
Abstract: Social conventions are useful for the coordination of multi-agent systems. Decentralized models of social
convention emergence have demonstrated that global agreement can be the result of local coordination
behaviors without the need for any central control and authority. Convention arises through a co-learning
process from repeated interactions, where the history of interactions plays a fundamental role in the learning
process. The main research goal of this work is to study the role of ties in the standard frequency model
called External Majority (EM). In the External Majority case agents change to a new convention only if a
different convention was more often seen than the current one in the last μ interactions. Agents prefer to
conserve their conventions if the current one is included in the set of the most often seen in the last μ
encounters. We study three variations in EM behaviors regarding the way of dealing with tie situations and
study empirically their impact on convention emergence efficiency. Efficiency is a decisive property in what
concerns the design of large-scale self-organizing artificial systems, and one of the variations we propose
strongly improves consensus emergence performance.
1 INTRODUCTION
Distributed coordination is the outcome of dynamic
collective behavior where independent agents are
able to coordinate their actions without the need of a
central coordinator (Shoham and Tenneholtz, 1997).
Decentralized models of social convention
emergence (Lewis, 1969) have demonstrated that
global agreement can be the result of local
coordination behaviors without the need for any
central control and authority in populations
organized in networks of different topologies
(Delgado, 2002; Kaplan, 2005; Kittock, 1995;
Shoham and Tenneholtz, 1992; Walker and
Wooldridge, 1995; Villatoro et al, 2009).
Conventions can arise through a social co-learning
process from repeated interactions, where the history
of interactions plays a fundamental role in the
learning process.
Conventions specify a choice common to all
agents in a population, and are a straightforward
means for achieving coordination in a multi-agent
system. The issue at stake here relates to collective
choice and coordination mechanisms: a
homogeneous group is in presence of several
potential conventions and has to select one of them.
As conventions are considered equally good, what is
important is that the choice is consensual (the
particular chosen convention is irrelevant). An
example of such norm is the lane of traffic on a
given country. It is irrelevant whether right lane or
left lane is chosen, as long as everybody uses the
same.
One related area is Semiotic Dynamics (Steels,
1995) where the goal is to attain a shared language
in a population of artificial agents. It has been shown
that, starting from complete disagreement, simple
models of interacting agents can display a global
agreement on shared mapping between words and
objects, developing specially a shared system of
linguistic conventions (Steels, 1997; Kirby, 2002;
Barr, 2004). Curiously, recent spread on tagging
systems on the web, like del.icio.us or flickr.com,
has increased the motivation to understand these
self-organizing human phenomena related to
language emergence.
The main research goal in this work is to study
the role of ties in the External Majority (EM)
standard co-learning behavior (Shoham and
Tenneholtz, 1997), which is a frequency model. In
the External Majority model, N identical agents start
by choosing randomly a convention among a fixed
321
Urbano P., Balsa J., Ferreira P. and Baptista J..
THE IMPORTANCE OF TIES IN THE EFFICIENCY OF CONVENTION EMERGENCE .
DOI: 10.5220/0003189403210329
In Proceedings of the 3rd International Conference on Agents and Artificial Intelligence (ICAART-2011), pages 321-329
ISBN: 978-989-8425-41-6
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

set. At each time step, a pair of neighboring agents is
chosen randomly, and a learning process takes place
according to the following rule: adopt the
convention most frequently seen during the last μ
interactions, i. e., change to a new convention only if
a different convention was more often seen than the
current one in the last μ interactions. Agents have a
memory, which can be limited (registering only the
last μ interactions) or unlimited (registering every
encounter). In what regards ties, in EM, agents
prefer to conserve their conventions if the current
one is included in the set of the most often seen in
the last μ encounters but there are some situations
left unspecified.
Thus, we will complete the standard EM
behavior definition (first variation), we will develop
two other variations of EM regarding the way of
dealing with tie situations, and study empirically
their impact on convention emergence efficiency.
Efficiency will be measured in terms of the average
number of interactions needed to achieve agreement,
along a sufficient set of simulations, where each
simulation ends after a certain level of consensus is
attained.
Considering a tie set T of most frequently seen in
the last μ encounters, the three variations studied
are:
1. Conservative. Prefer the currently adopted
convention if it is in the most frequently seen set (T)
otherwise prefer the convention that was last seen
from the set;
2. Last. From the set T select the convention that
was last seen, and
3. Random. Choose randomly one of T elements.
We will deal only with fully connected topologies
but convention emergence will be compared along
three important dimensions: the number of agents,
the convention space size and the memory size of
agents. Note that EM is equivalent to another classic
behavior, the Highest Cumulative Reward (HCR)
(Shoham and Tennenholtz, 1992) in situations where
there are only two conventions in competition. In
HCR, agents change to a new convention only if
there is another convention that has received a
higher reward than the current adopted one during
the last μ interactions. Thus, our results can be
applied to HCR with binary convention spaces. The
voter model (Krapivsky, 1992) is very similar to the
External Majority model but, instead of binary
interactions, agents interact simultaneously with
several agents deciding in a unique encounter to
adopt the most frequently convention seen on their
neighbors.
The issue of self-organization of convention
development is of the outmost importance for the
design of collective artificial systems, where it is
obvious that the convention emergence has to take
place as quickly as possible. This is the main
motivation of this paper: trying to find behaviors
which are simple enough but can attain high
performances in terms of efficiently bootstrapping a
shared consensual convention system.
The structure of this paper is as follows: in
section 2, we begin by describing the concept of
Convention Problem, then we characterize
convergence efficiency, and finally we introduce the
External Majority (EM) convention update rule. In
section 3 we explain the incomplete EM behavior
rule regarding tie situations and introduce the three
behaviors (in fact three variations of EM) which are
perfectly equivalent except in the way of dealing
with tie situations. In Section 4 we present the
experiments and their results, which are analyzed,
and finally we conclude.
2 THE EMERGENCE
OF CONVENTIONS
2.1 Convention Problem
De Vylde (Vylde, 2008) introduced the concept of
Convention Problem, which is a description of a
system of interacting agents, which try to reach an
agreement. This description specifies several aspects
external to the agents’ architecture and behavior,
like the Convention Space (topics on which
agreement must be reached), Interaction Model
(interaction style and the society topological
structure), and the Information Transfer Model
(what information is transferred during agent
interaction).
A Convention Space is the space of alternatives
from which the agents have to make a collective
choice. We can have continuous or discrete
alternative spaces, we can have structured or
unstructured (flat) convention spaces. “A convention
space is unstructured if the only thing we can say
about two alternatives is whether they are equal or
not” (Vylde, 2008).
The Interaction Model deals with the topology of
the agents’ network, with fixed or dynamic
populations, with the number of agents involved in
each interaction, with the roles played by them
during interactions, with the frequency of
interactions and with the property related with the
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
322

awareness or the absence of awareness regarding
each other’s identity.
The Information Transfer Model deals with the
nature of interactions. One important aspect is the
information that is transmitted during encounters.
Agents can have access to the conventions played by
their interacting partners during encounters or they
can just receive a payoff or some other information.
In the following sections we characterize the
specific Convention Problem used in our research.
2.2 Convention Space
In this paper, we consider only discrete and
unstructured (flat) convention spaces. Regarding
size, we will deal with binary (2 conventions) and
N-ary (N different conventions for N agents)
conventions spaces. We could, of course, study
spaces with 3, 4 and more conventions but for now
we experiment with these two cases because they
represent two extreme situations, that represent the
two extremes in convention space size. Our
convention space is composed of discrete abstract
tokens that can be whatever we want. For example a
binary convention space can represent two
competing driving conventions: driving on the left
and driving on the right. For example, an N-ary
convention space can represent situations where the
goal is to give a name to an object. Each agent can
have its own name and by interacting it is desirable
that they will all adopt the same word for the object,
reaching a consensus and a shared lexicon.
2.3 Interaction Model
We will deal with fixed populations composed of
identical individuals. At time t, two players will be
selected to interact, where one of them is randomly
chosen and the other will be randomly chosen
among its neighbors, according to the social graph.
We will only consider fully connected networks
where each agent has all the others as neighbors.
During an interaction, between two neighboring
agents, they exchange information that may lead to
an update in their adopted conventions.
Agents that are not chosen to interact at a
particular instant t will have their state and
conventions unchanged.
The properties of an equivalent strategy update
rule (HCR) were studied for more complex
topologies in (Delgado, 2002; Kittock, 1995) and
other co-learning behaviors were studied for
different social topologies (Villatoro et al., 2009,
2009b).
2.4 Information Transfer Model
During an interaction agents can play one or both of
two possible roles (Speaker or Hearer). When an
agent plays the Speaker role it communicates to the
other its currently adopted convention. The Hearer
agent hears the convention of its partner and updates
its own convention to reflect the new information.
We can have unilateral pair wise encounters
where each agent plays a different role: one of them
is the hearer and the other is the speaker. In
contrast, during bilateral encounters both agents
speak and hear, exchanging conventions (speaking)
before updating them (hearing).
Returning to De Vylde’s framework, the
information that is transferred between agents is
only the conventions they are adopting during an
encounter, when they are playing the speaker role.
Agents do not have access to the experiences of
others (their memories of past events).
2.5 Measuring Efficiency
There are different possible measures regarding
convergence emergence efficiency. Shoham and
Tennenholtz (Shoham and Tenneholtz, 1992, 1997)
used the probability of achieving a fixed
convergence level after a fixed number of random
pairwise encounters. The number of agents selecting
the most adopted convention divided by the
population size is named the convergence level.
Kittock (Kittock, 1993) introduced the average
number of encounters for a fixed convergence level
— he used a convergence level of 90%. Starting
from a situation where each agent chooses its initial
convention randomly from the convention space, a
simulation is run, time step after time step, until a
fixed convergence level is reached and we register
the number of encounters, which are averaged over a
number of sufficient simulations. Other measures
can be used like the average convergence level after
a fixed number of encounters. Besides the average
measured over a number of simulations, it can be
useful the minimum and the maximum values.
We have chosen Kittock measure, the average
number of encounters necessary for reaching a
consensual level of 90%.
2.6 External Majority
N identical agents try to reach an agreement
regarding convention, and they have direct access to
the conventions selected by their partners through
pair wise interactions. Memory is used to register the
THE IMPORTANCE OF TIES IN THE EFFICIENCY OF CONVENTION EMERGENCE
323

conventions observed during the last μ interactions.
The External Majority convention update rule (EM)
was introduced by Shoham and Tennenholtz
(Shoham and Tenneholtz, 1997) and is the
following: if, in the last μ interactions, some
convention was more frequently seen that the current
one, adopt that convention, otherwise keep the
current convention. EM coincides with HCR
(Shoham and Tenneholtz, 1997) in a convention
space composed of two conventions. Working with
fully connected graphs, Shoham and Tennenholtz
(Shoham and Tenneholtz, 1992, 1997) provided a
theorem that guarantees that a consensual
convention will be attained if agents apply HCR and
they predicted analytically a lower bound of
O(NlogN) in efficiency based on the variation on the
number N of agents in the population. Kittock
(Kittock, 1995) empirical results also suggest
O(NlogN). Shoham and Tenneholtz (Shoham and
Tenneholtz, 1992, 1997) stated that “it pays to
forget” and “that old history of the agents is less
adequate than the relatively new information, and as
a result it may be better not to rely on old
information as part of the data a decision refers to.
On the other hand, too short memory may not enable
the agents enough sampling of what is going on in
the system, and may lead to inefficient behavior.”
Both Kittock (Kittock, 1993) and (Delgado, 2002) in
their HCR bilateral experiments in binary
convention spaces (equivalent to EM) have used
always a memory size of 1 for different population
sizes, network topologies and convention space
sizes. But, in (Urbano et al, 2009) Urbano et al
concluded that the optimal memory sizes depend on
the network topologies, the number of agents and the
dimension of convention spaces.
2.7 Agent Model for External Majority
There is a population of N identical agents where
each agent is defined by a convention and a memory
with size μ. The μ parameter may not have limit,
implying that the full history of pairwise meetings
will play a role in the convention selection process,
or we can implement a forgetting mechanism by
limiting μ. It was Shoham and Tennenholtz (Shoham
and Tenneholtz, 1992) that have introduced a
mechanism of forgetting. In fact, they have
introduced two forms of limited memory windows:
one in which an agent remembers the last μ events in
which it participated in a interaction and another
where memory was assumed to record the last μ
encounters during which an agent might interact
many, few, or no times. We will follow the first
memory type where agents register only their μ last
meetings. The agents’ memories register the
conventions that were seen during their last μ
encounters. When an agent interacts with another
agent during a pairwise encounter, he will eventually
have to discard the oldest event to maintain memory
at a fixed size. The memory of agent k, M
k
, is
modeled as a set of events. An event e belonging to
M is represented as pair, e =

t
e
,c
e
 , where c
e
is the
convention seen at time t
e
.
At time t, two players will be selected to interact,
where one of them is randomly chosen and the other
will be randomly chosen among its neighbors,
according to the social graph. The agent playing the
speaker role, will present the hearer its current
convention. The agent playing the hearer role will
first forget its oldest event, if it is the case that its
memory is full, then it will choose its new
convention based on its memory contents and its
partner convention and only then it will register the
new event. Agents that are not chosen to interact at a
particular instant t will have their memory and
conventions unchanged.
3 TIES: THREE VARIATIONS
ON EXTERNAL MAJORITY
BEHAVIOR
How does EM deals with ties? Do they play a
relevant role regarding performance? And is there a
different and better way to deal with ties? In EM
with full history of encounters we know that in case
of a tie the current convention is always adopted.
And logically it is impossible to have a tie without
the current convention in the group of the most
frequently seen. The same happens when there is a
binary convention space and agents have limited
memory—there are only two conventions and the
currently adopted must be in the tie group. Now let’s
analyze EM update rule regarding ties in face of
spaces of conventions with more than two elements
when agents use a limited memory. But in situations
with limited memory, one of the events in memory
involving current convention may be forgotten and
we can have a situation where two or more
conventions, different from the current one, are
competing to be selected. How EM deals with this
situation? EM definition is not clear and perhaps a
precise tie solving was not considered significantly
relevant and was left open. Perhaps random choice
was implicit. We did not find in the literature any
reference to the importance of dealing with ties of
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
324

this type. Perhaps the reason is obvious: most of the
research made with EM considered spaces of two
conventions where tie situations of this type can
never occur.
3.1 Completing EM definition:
Conservative
We are going to complete External Majority
definition, we call it the “conservative” tie strategy
of External Majority regarding the special tie
situation when currently adopted convention is not
in the set of the most frequently observed in the last
μ encounters. In tie situations where T is the set of
the most frequently observed conventions in the last
μ encounters.
1: If current convention belongs to T, stick to it.
2: Otherwise select the most recently observed from
the set T.
3.2 A Variation in EM: Last
We are going to introduce a second variation in the
EM convention update rule, regarding ties. Our EM
variation, the “last” tie strategy, is the following:
adopt the convention that was observed more often
in other agents in the last μ interactions, and in case
of a draw adopt the most recently observed
convention from the tie set. The motivation for this
variation is quiet evident. It may be better to choose
the most recently observed—perhaps it indicates that
the convention is still around and it is a winner.
3.3 A Variation in EM: Random
In case we have a tie we just choose randomly one
the most frequently seen conventions in the last μ
interactions. External Majority with a random choice
for solving ties, corresponds with some small
differences to a model introduced by Kaplan
(Kaplan, 2000, 2005). He only considered unilateral
encounters and no forgetting but he found a
convergence of N(logN) for both binary and N-ary
convention spaces.
4 EXPERIMENTAL RESULTS
Agents initially pick randomly one of two
conventions in the case of binary spaces and a
unique convention in the case of N-ary spaces.
We are going to compare the three EM tie
strategies for fully connected networks, where every
agent can interact with any other and interactions
will be both unilateral, and bilateral. We will choose
90% of level consensus and will count the average
number of encounters needed to attain such a
convergence level, averaged over 500 runs.
We have performed comparison experiments for
agents that register the full history of encounters and
for agents with optimal memories (it will be
explained later). We used populations composed by
100, 200, 300, 400…1000, 2000…10000,
20000…50000 agents except in some bilateral
experiments.
Besides showing the average number of
interactions necessary for attaining a 90% level of
consensus, as the performances are difficult to
compare with log-log graphs, we have shown for
each situation the percentage of efficiency gain for
using Last EM. The percentage of efficiency gain is
calculated this way:
P
PerfomanceLast
P

where P can be the performance of the Conservative
EM or the Random EM.
For example, considering a population of 1000
agents, a binary convention space, and unilateral
interaction, if for the Last tie strategy, we obtain a
performance of 800, and for the Conservative
strategy, a performance of 1000, the efficiency gain
will be 0,2, which means that Last represents a 20%
increment in efficiency.
4.1 Full History Unilateral Agents
For full history agents with unilateral interactions,
results (performance and efficiency gain) are
presented from figures 1 to 4, both for binary and N-
ary convention spaces.
Com
p
arison of Performance: Full Histor
y
of Unilatera
l
Encounters (Binary Spaces)
100
1000
10000
100000
1000000
10000000
100 1000 10000 100000
Number of Agents
Last
Conservative
Random
Figure 1: Comparison of the average number of unilateral
interactions necessary for attaining a 90% consensus for
populations composed of agents with full history along
binary convention spaces. Results are derived from 500
simulations.
THE IMPORTANCE OF TIES IN THE EFFICIENCY OF CONVENTION EMERGENCE
325

Efficiency Gain: Full History of Unilateral (binary spaces)
0,00%
5,00%
10,00%
15,00%
20,00%
25,00%
30,00%
100 1000 10000 100000
Number of Agents
Gain over Conservative Gain over Random
Figure 2: The efficiency gain of Last EM for populations
composed of agents with full history along binary
convention spaces and unilateral interactions. Results are
derived from 500 simulations.
Com
p
arison of Performance: Full Histor
y
of Unilateral Encounters
(N
ary Spaces)
1000
10000
100000
1000000
10000000
100 1000 10000 100000
Number of Agents
Last
Conservative
Random
Figure 3: Comparison of the average number of unilateral
interactions necessary for attaining a 90% consensus for
populations composed of agents with full history along N-
ary convention spaces. Results are derived from 500
simulations.
Efficienc
y
Gain: Full Histor
y
Unilateral
(
N-ar
y
S
p
aces
)
0,00%
10,00%
20,00%
30,00%
40,00%
50,00%
60,00%
70,00%
100 1000 10000 100000
Number of Agents
Gain over Conservative Gain over Random
Figure 4: The efficiency gain of Last EM for populations
composed of agents with full history along N-ary
convention spaces and unilateral interactions. Results are
derived from 500 simulations.
Our results show that the Last EM variation
produces a substantial increase in efficiency,
especially for N-ary convention spaces (figures 3
and 4) where efficiency is dramatically increased
with population size and correspondingly with the
convention space size (recall that the N-ary scenario
means a unique convention per agent). For 100
agents, the gain is around 15%. In what concerns
populations of 50 000 agents, the reduction on the
average number of encounters necessary for a 90%
consensus is almost 70% (compared with the
Conservative EM variation) and almost 60%
(compared with the Random EM variation), which is
a remarkable result.
This pattern of increase in efficiency gain with
population size is not observed when we have binary
convention spaces (figures 1 and 2). But even here
the increase in efficiency is on average 18,83% and
10,41% compared with the Conservative and
Random respectively.
4.2 Full History Bilateral Agents
The experiments with bilateral encounters in
societies with full history agents are described in
figures 5 and 6, for the binary case, and figures 7
and 8, for the N-ary case.
Comparison of Performance: Full History of Bilateral Encount
e
(Binary Spaces)
100,00
1000,00
10000,00
100000,00
1000000,00
10000000,00
100 1000 10000 100000
Number of A
g
ent
s
Last
Conservative
Random
Figure 5: Comparison of the average number of bilateral
interactions necessary for attaining a 90% consensus for
populations composed of agents with full history along
binary convention spaces. Results are derived from 500
simulations.
Slightly inferior results are observed with
bilateral interaction. In the binary space case the
average gain in performance is 12,15% and 2,76%
(figure 6) compared with Conservative and Random.
In same cases Random variation is better than the
Last. But in the N-ary scenario the improvement in
performance is again substantial, increasing with the
number of agents and correspondingly with the size
of convention space. The gain compared with the
Conservative is almost 60% for 50000 agents and
around 50% for 20000 when compared with
Random. The performances of Randoms and
Conservatives are equivalent in the N-ary case, but
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
326

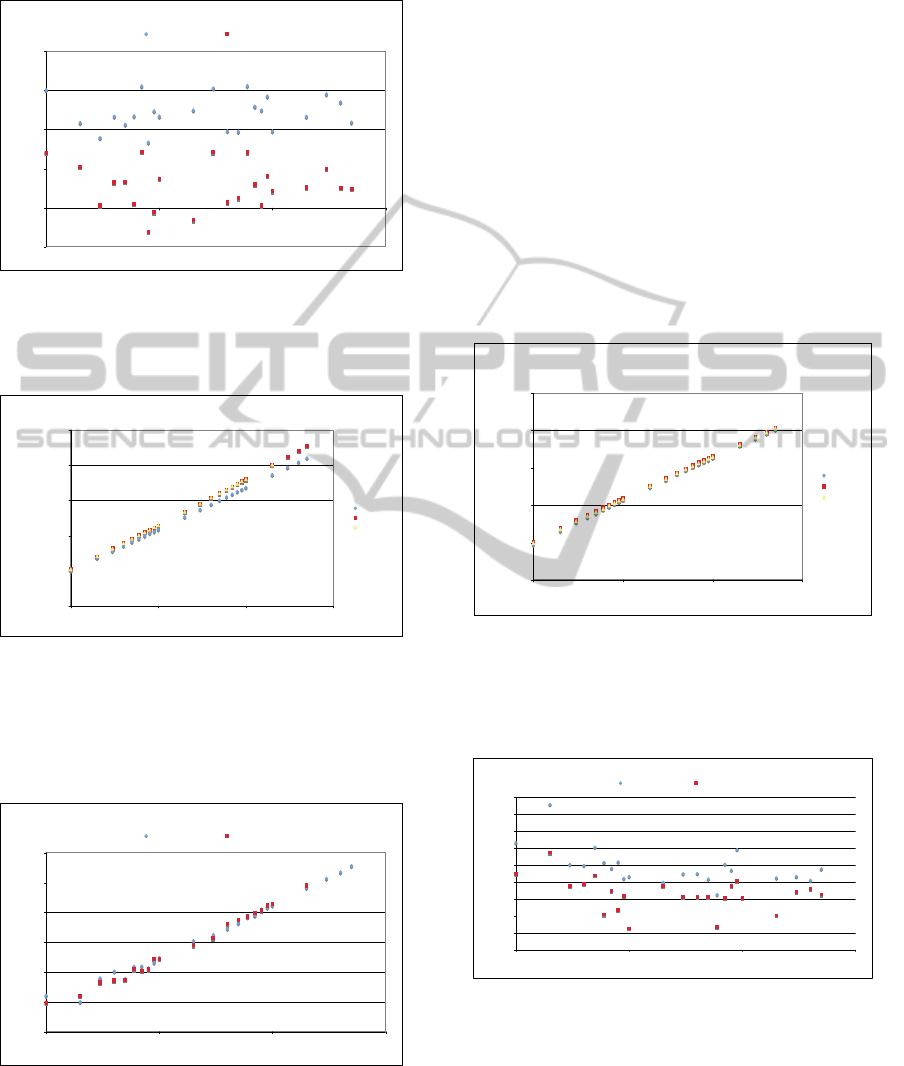
the Randoms attain 90% of consensus on average in
10% less encounters than Conservatives.
Efficienc
y
Gain: Full Histor
y
of Bilateral Encounters
(
Bina
r
-5,00%
0,00%
5,00%
10,00%
15,00%
20,00%
100 1000 10000 100000
Number of A
g
e
n
Gain over ConservativeGain over Rand
o
Figure 6: The efficiency gain of Last EM for populations
composed of agents with full history along binary
convention spaces and bilateral interactions. Results are
derived from 500 simulations.
Comparison of Efficiency: Full History of Bilateral Encounters (N-ary Spa
c
100,00
1000,00
10000,00
100000,00
1000000,00
10000000,00
100 1000 10000 100000
Number of A
g
ent
s
Last
Conservative
Random
Figure 7: Comparison of the average number of bilateral
interactions necessary for attaining a 90% consensus for
populations composed of agents with full history along N-
ary convention spaces. Results are derived from 500
simulations. Note that for the Random strategy the
maximum number of agents is 20000.
Efficiency Gain: Full History of Bilateral Encounters (N-ary
0,00%
10,00%
20,00%
30,00%
40,00%
50,00%
60,00%
100 1000 10000 100000
Number of A
g
e
n
Gain over ConservativeGain over Rando
Figure 8: The efficiency gain of Last EM for populations
composed of agents with full history along N-ary
convention spaces and bilateral interactions. Results are
derived from 500 simulations. Note that for the Random
strategy the maximum number of agents is 20000.
4.3 Optimal History Unilateral Agents
We have measured the performance of limited
memory agents with optimal memory size. In order
to obtain optimal memory sizes we have varied the
memory size, looking for the one that exhibited best
performance. We have searched for the optimal
memory size for each situation (EM variation,
number of agents, convention space size, and
interaction type) and choose the correspondent
optimal performance. We won’t show here the effect
that different memory sizes have on performance
due to limitation of space.
In figures 9, 10, 11 and 12 we show the results of
the experiments regarding optimal memory sizes for
unilateral interaction, in both binary and N-ary
convention spaces.
Com
p
arison of Performance: O
p
timal Histor
y
of Unilateral Encou
n
Spaces)
100
1000
10000
100000
1000000
10000000
100 1000 10000 100000
Number of A
g
e
n
Last
Conservati
v
Random
Figure 9: Comparison of the average number of unilateral
interactions necessary for attaining a 90% consensus for
populations composed of agents with best memory sizes
along binary convention spaces. Results are derived from
500 simulations.
Efficiency Gain: Optimal History of Unilateral (Binary Spaces
)
0,00%
2,00%
4,00%
6,00%
8,00%
10,00%
12,00%
14,00%
16,00%
18,00%
100 1000 10000 100000
Number of Agents
Gain over Conservative Gain over Random
Figure 10: The efficiency gain of Last EM for populations
composed of agents with best memory sizes along binary
convention spaces and unilateral interactions. Results are
derived from 500 simulations.
In what regards binary spaces we see again a
small improvement on performance by the Last EM
variation (figure 10): 9,66% and 6,55% on average
compared to Conservative and Random. But again a
THE IMPORTANCE OF TIES IN THE EFFICIENCY OF CONVENTION EMERGENCE
327

substantial improvement in the case of N-ary
convention spaces, increasing with population size: a
gain of efficiency of almost 60% for a population of
50000 for the Last variation compared with both
Random and Conservative (figure 12).
Com
p
arison of Performance: O
p
timal Histor
y
of Unilateral En
c
ary Spaces)
100
1000
10000
100000
1000000
10000000
100 1000 10000 100000
Number of A
g
e
n
Last
Conservati
v
Random
Figure 11: Comparison of the average number of unilateral
interactions necessary for attaining a 90% consensus for
populations composed of agents with best memory sizes
along N-ary convention spaces. Results are derived from
500 simulations.
Efficiency Gain: Optimal History of Unilateral Encounters (N-ary Spaces)
0,00%
10,00%
20,00%
30,00%
40,00%
50,00%
60,00%
100 1000 10000 100000
Number of Agents
Gain over Random Gain over Conservative
Figure 12: The efficiency gain of Last EM for populations
composed of agents with best memory sizes along N-ary
convention spaces and unilateral interactions. Results are
derived from 500 simulations.
4.4 Optimal History Bilateral Agents
In what regards bilateral encounters, our
experimental results are depicted from figures 13 to
16. As in the unilateral case, we have searched for
the memory sizes which have performed optimally
and the three variations are compared along
scenarios with optimal memory sizes. As a curiosity
we have noticed that the optimal memory sizes are
in general bigger than in the unilateral case but that
will not be discussed here.
Notice that Last continues to win, slightly in
binary spaces (7,16% on average compared with
Conservative and 3,47% on average compared with
Random), but with more significance in N-ary
spaces, although not so substantial as in the full
history case. Nevertheless, for 10000 agents there is
an increase of 30% in the efficiency of the Last
compared with the others, which are equivalent, and
this result increases with population size.
Com
p
arison of Performance: O
p
timal Histor
y
of Bilateral Encoun
t
(Binary Spaces)
100
1000
10000
100000
1000000
100 1000 10000
Number of A
g
ent
s
Last
Conservative
Random
Figure 13: Comparison of the average number of bilateral
interactions necessary for attaining a 90% consensus for
populations composed of agents with best memory sizes
along binary convention spaces. Results are derived from
500 simulations.
Efficiency Gain: Optimal History of Bilateral Encounters (Bina
-5,00%
0,00%
5,00%
10,00%
15,00%
20,00%
100 1000 10000
Number of A
g
e
n
Gain over ConservativeGain over Rand
o
Figure 14: The efficiency gain of Last EM for populations
composed of agents with best memory sizes along binary
convention spaces and bilateral interactions. Results are
derived from 500 simulations.
Com
p
arison of Performance: O
p
timal Histor
y
of Bilateral Encounters
(
N-ar
y
Spaces)
100,00
1000,00
10000,00
100000,00
1000000,00
100 1000 10000
Number of Agents
Last
Conservative
Random
Figure 15: Comparison of the average number of bilateral
interactions necessary for attaining a 90% consensus for
populations composed of agents with best memory sizes
along N-ary convention spaces. Results are derived from
500 simulations.
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
328

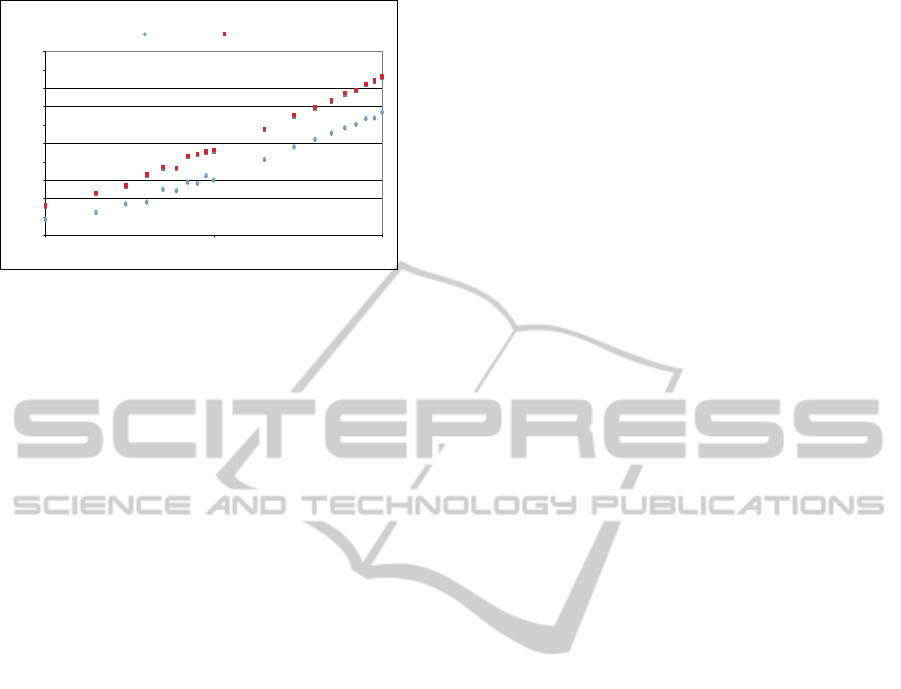
Efficienc
y
Gain: O
p
timal Histor
y
of Bilateral Encounters
(
N-
a
0,00%
5,00%
10,00%
15,00%
20,00%
25,00%
30,00%
35,00%
40,00%
45,00%
50,00%
100 1000 10000
Number of A
g
e
n
Gain over ConservativeGain over Rand
o
Figure 16: The efficiency gain of Last EM for populations
composed of agents with best memory sizes along N-ary
convention spaces and bilateral interactions. Results are
derived from 500 simulations.
5 CONCLUSIONS
We have made experiments with three variations on
a standard frequency model of distributed
coordination in multi-agent systems, regarding
convention emergence. These agents are able to
interact with the others observing the choices
selected by them based on a simple local adaptation
rule, which depends only on the history of their
interactions. The rule, named External Majority, is
the following: select the convention most frequently
seen in the last μ encounters. In particular we have
studied the impact of ties on the efficiency of a
consensual choice inside a population of
independent and self-organized agents. From the
results we may conclude that ties play a very
important role regarding the quantitative
improvement on the efficiency of convention
emergence over the standard External Majority, in
fully connected networks, when there are both
unilateral and bilateral encounters between agents.
In particular the variation on the External
Majority that says that prefer the most seen
convention and in case of ties prefer the most
recently seen has a dramatic effect on performance
attaining high levels of gain, specially for big
population sizes and increasing with population size.
In the future we will extend the experiments to
other networks topologies and higher population
sizes and look for agents with dynamic memory
sizes, which will adapt to population size, the social
graph topology and the size of convention spaces.
REFERENCES
Barr, D. J., 2004. Cognitive Science, 28, 185-215.
Delgado, J., 2002. Emergence of social conventions in
complex networks. Artificial Intelligence, 141
(1/2):171-185.
Kaplan, F., 2000. L’Emergence D’un Lexique Dans Une
Population d’Agents Autonomes. PhD thesis,
Université de Paris 6, (2000).
Kaplan, F., 2005. Simple models of distributed co-
ordination, Connection Science, 17 (3-4): 249-270.
Kirby, S., 2002. Artificial Life 8, 185-215.
Kittock, J. E., 1995. Emergent conventions and the
structure of multi-agent systems. In L. Nadel, D. Stein
(Eds.), 1993 Lectures in Complex Systems, in: SFI
Studies in the Sciences of Complexity. Addison-
Wesley, Reading, MA.
Krapivsky, P., 1992. Kinetics of monomer-monomer
surface catalytic reactions. Phys. Rev. A, 45: 1067-
1072.
Lewis, D., 1969. Convention: A philosophical study.
Harvard University Press.
Shoham, Y. and Tennenholtz, M., 1992. Emergent
Conventions in Multi-Agent Systems: initial
experimental results and observations. In Nebel, B.,
Rich, Ch., Swartout, W., (Eds.) Proc. of the 3rd Int.
Conference of Knowledge Representation and
Reasoning, Morgan Kaufmann, San Mateo, CA, pages
225-231.
Shoham, Y., Tennenholtz, M., 1997. On the emergence of
social conventions: Modelling, analysis and
simulations. Artificial Intelligence 94, pages 139-337.
Steels, L., 1995. The Talking Heads Experiment. Volume
1. Words and Meanings. Laboratorium. Antewerpe.
Steels, L., 1997. Evolution Communication, 1. 1.
Urbano, P. Balsa, J., Ferreira Jr., P. and Antunes, L., 2009.
How Much Should Agents Remember? The Role of
Memory Size on Convention Emergence Efficiency,
MASTA—EPIA’09.
Villatoro, D., Malone, N. and Sen S., 2009. Effects of
interaction history and network topology on rate of
convention emergence. In Proc. of the 3rd Int.
Workshop on Emergent Intelligence and Networked
Agents (WEIN’09).
Villatoro, D., Sen, S. and Sabater-Mir, J., 2009b.
Topology and memory effect on convention
emergence. In Proc. of the IEEE/WIC/ACM
International Conference on Intelligent Agent
Technology (IAT 2009).
Vylde, B. D., 2008. The Evolution of Conventions in
Multi-Agent Systems. PhD Thesis, Free University of
Brussels.
Walker, A., Wooldridge, M., 1995. Understanding the
emergence of conventions multi-agent systems. In
Lesser, V. (ed.), Proc. 1st Int. Conf. on Multi-Agent
Systems, AAAI Press, pages 384-389.
THE IMPORTANCE OF TIES IN THE EFFICIENCY OF CONVENTION EMERGENCE
329