COMPLETE DISTRIBUTED CONSEQUENCE FINDING WITH
MESSAGE PASSING
Katsumi Inoue, Gauvain Bourgne
National Institute of Informatics, 2-1-2 Hitotsubashi, Chiyoda-ku, Tokyo, Japan
Takayuki Okamoto
Graduate School of Science and Technology, Kobe University, 1-1 Rokkodai-cho, Nada-ku, Kobe, Japan
Keywords:
Consequence finding, Distributed reasoning, Multi-agent systems.
Abstract:
When knowledge is physically distributed, information and knowledge of individual agents may not be col-
lected to one agent because they should not be known to others for security and privacy reasons. We thus
assume the situation that individual agents cooperate with each other to find useful information from a dis-
tributed system to which they belong, without supposing any master or mediate agent who collects all nec-
essary information from the agents. Then we propose two complete algorithms for distributed consequence
finding. The first one extends a technique of theorem proving in partition-based knowledge bases. The second
one is a more cooperative method than the first one. We compare these two methods on a sample problem
showing that both can improve efficiency over a centrlized approach, and then discuss other related approaches
in the literature.
1 INTRODUCTION
There is a growing interest in building large knowl-
edge bases. Dealing with a huge amount of knowl-
edge, two problems can be encountered in real do-
mains. The first case is that knowledge is originally
centralized so that one can access the whole knowl-
edge but the knowledge base is too huge to be han-
dled. The second case is that knowledge is distributed
in several sources so that it is hard or impossible to
immediately access the whole or part of knowledge.
The former case is studied in the line of research on
parallel or partition-based reasoning. For example,
partition-based theorem proving by Amir and McIl-
raith (Amir et al, 2005) divide a knowledge base into
several parts each of which is easier to be handled so
that the scalability of a reasoning system is improved.
On the other hand, in the second case we suppose
multi-agent systems or peer-to-peer systems (Adjiman
et al, 2006), in which an agent does not want to ex-
pose all its information to other agents for security
and privacy reasons. Sometimes, it is inherently im-
possible to tell what other agents want to know and to
ask what can be obtained from others. In such a case,
each agent must give up gathering all necessary infor-
mation from other agents, and moreover, no master or
mediate agent can be assumed to exist to collect all
information from agents. That is, we need to solve
the problem with knowledge distributed as it is. In
this research, we mainly deal with such distributed
knowledge bases, but hope that those algorithms con-
sidered for distributed reasoning can be applied to the
first case to gain efficiency.
In this work, we consider the problem of dis-
tributed consequence finding. Consequence find-
ing (Lee, 1967; Inoue, 1992; Marquis, 2000) is a
problem to discover an interesting theorem deriv-
able from an axiom set, and is a promising method
for problem solving in AI such as query answering
(Iwanuma et al, 2002), abduction (Inoue, 1992; In-
oue et al, 2009; Nabeshima et al, 2010), induction
(Nienhuys-Cheng et al, 1997; Inoue, 2004), diagno-
sis, planning, recognition and understanding. There
are some complete procedures for consequence find-
ing in first-order clausal theories (Inoue, 1992; del
Val, 1999) and efficient systems have also been devel-
oped (Nabeshima et al, 2003; Nabeshima et al, 2010).
Our concern here is to design a complete method in
the distributed setting, that is, to obtain every conse-
quence that would be derived from the whole knowl-
edge base if it were gathered together. In this paper,
we propose two new methods for distributed conse-
134
Inoue K., Bourgne G. and Okamoto T..
COMPLETE DISTRIBUTED CONSEQUENCE FINDING WITH MESSAGE PASSING.
DOI: 10.5220/0003190001340143
In Proceedings of the 3rd International Conference on Agents and Artificial Intelligence (ICAART-2011), pages 134-143
ISBN: 978-989-8425-41-6
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

quence finding.
The first method here is a generalization of
partition-based theorem proving by (Amir et al, 2005)
to consequence finding. The whole axiom set is par-
titioned into multiple sets called partitions, each of
which can be associated with one agent. In this
method, a pair of partitions must be connected with
their communication language. The connections be-
tween partitions constitute a graph, but cycles must
be removed so that the graph is transferred to a tree.
Consequence finding is firstly performed in the leaves
of the connection tree, and its consequences are sent
to the parent if they belong to the communication lan-
guage. This process is repeated until the root. To get
a complete procedure in this method, it is important
to decide the communication languages between two
partitions, so we propose the method to determine
them. It should be stressed that, although partition-
based theorem proving by (Amir et al, 2005) also uses
a consequence finding procedure in each individual
reasoning task of an agent, the aim of (Amir et al,
2005) is not consequence finding from the knowledge
base but is used for theorem proving tasks.
The second proposed method is a more coopera-
tive one. In this method, we do not presuppose graph
structures of agents, but any agent has a chance to
communicate with other agents, hence the framework
is more dynamic than the first method. Firstly, a new
clause is added to an agent A
1
, either as a top clause
of the given problem or as a newly sent message from
other agents, which then triggers consequence find-
ing from that clause with the axioms of A
1
. Then,
for each such newly derived clause C, if there is a
clause D in the axiom set of another agent A
2
such
that C and D can be resolved, then C is sent to A
2
and is added there. This process is repeated until no
more new clause can be resolved with any clause of
any other agent. We will compare these two meth-
ods and centralized approaches, and discuss the mer-
its and demerits of both methods. We will also discuss
relations with other previously proposed approaches
to consequence finding in distributed settings (Inoue
et al, 2004; Adjiman et al, 2005; Adjiman et al, 2006).
The rest of this paper is organized as follows. Sec-
tion 2 reviews the background of consequence finding
and SOL resolution. Section 3 proposes partition-
based consequence finding. Section 4 proposes a
more cooperative algorithm for consequence finding
and Section 5 compares the two proposed approaches.
Section 6 discusses related work, and Section 7 gives
a summary and future work.
2 CONSEQUENCE FINDING
In this section, we review consequence finding from
an axiom set and a complete procedure for it. The
task of consequence finding is related with many AI
reasoning problems, and is indispensable in partition-
based theorem proving in Section 3.1 too.
A clause is a disjunction of literals. Let C and D
be two clauses. C subsumes D if there is a substitution
θ such that Cθ ⊆ D. C properly subsumes D if C sub-
sumes D but D does not subsume C. A clausal theory
is a set of clauses, which is often identified with the
conjunctive normal form (CNF) formula composed
by taking the conjunction of all clauses in it. Let Σ
be a clausal theory. µΣ denotes the set of clauses in Σ
not properly subsumed by any clause in Σ. A conse-
quence of Σ is a clause entailed by Σ. We denote by
T h(Σ) the set of all consequences of Σ.
The consequence finding problem was first ad-
dressed by Lee (Lee, 1967) in the context of the reso-
lution principle, which has the property that the con-
sequences of Σ that are derived by the resolution prin-
ciple includes µT h(Σ). To find “interesting” theorems
for a given problem, the notion of consequence find-
ing has been extended to the problem to find char-
acteristic clauses (Inoue, 1992). Each characteristic
clause is constructed over a sub-vocabulary of the rep-
resentation language called a “production field”. For-
mally, a production field P is a pair, hL, Condi, where
L is a set of literals closed under instantiation, and
Cond is a certain condition to be satisfied, e.g., the
maximum length of clauses, the maximum depth of
terms, etc. When Cond is not specified, P = hL,
/
0i is
simply denoted as hLi. A production field P is stable
if, for any two clauses C and D such that C subsumes
D, D belongs to P only if C belongs to P .
A clause C belongs to P = hL, Condi if every lit-
eral in C belongs to L and C satisfies Cond. For a set
Σ of clauses, the set of logical consequence of Σ be-
longing to P is denoted as T h
P
(Σ). Then, the charac-
teristic clauses of Σ with respect to P are defined as:
Carc(Σ, P ) = µ T h
P
(Σ). We here exclude any tautol-
ogy ¬L ∨ L (≡ True) in Carc(Σ, P ) even when both
L and ¬L belong to P . When P is a stable pro-
duction field, it holds that the empty clause  is the
unique clause in Carc(Σ, P ) if and only if Σ is unsat-
isfiable. This means that theorem proving is a special
case of consequence finding. The use of characteris-
tic clauses enables us to characterize various reason-
ing problems of interest to AI, such as nonmonotonic
reasoning, diagnosis, and knowledge compilation as
well as abduction and induction. In the propositional
case (Marquis, 2000), each characteristic clause of Σ
is a prime implicate of Σ.
When a new clause C is added to a clausal the-
COMPLETE DISTRIBUTED CONSEQUENCE FINDING WITH MESSAGE PASSING
135

ory Σ, further consequences are derived due to this
new information. Such a new and “interesting” clause
is called a “new” characteristic clause. Formally, the
new characteristic clauses of C with respect to Σ and
P are: Newcarc(Σ,C, P ) = µ [T h
P
(Σ ∧C) − T h(Σ) ].
When a new formula is not a single clause but a
clausal theory or a CNF formula F = C
1
∧ ··· ∧C
m
,
where each C
i
is a clause, Newcarc(Σ, F, P ) can be
computed as:
Newcarc(Σ, F, P ) = µ [
m
^
i=1
Newcarc(Σ
i
,C
i
, P ) ], (1)
where Σ
1
= Σ, and Σ
i+1
= Σ
i
∧C
i
, for i = 1, . . . , m− 1.
This incremental computation can be applied to get
the characteristic clauses of Σ with respect to P as
follows.
Carc(Σ, P ) = Newcarc(True, Σ, P ). (2)
Several procedures have been developed to com-
pute (new) characteristic clauses. SOL resolution (In-
oue, 1992) is an extension of the Model Elimination
(ME) calculus to which Skip operation is introduced
along with Resolve and Ancestry operations. With
Skip operation, SOL resolution focuses on deriving
only those consequences belonging to the production
field P . SFK resolution (del Val, 1999) is based on a
variant of ordered resolution, which is enhanced with
Skip operation for finding characteristic clauses. SOL
resolution is complete for finding Newcarc(Σ,C, P )
by treating an input clause C as the top clause and de-
rives those consequences relevant to C directly. SO-
LAR (SOL for Advanced Reasoning) (Nabeshima et
al, 2003; Nabeshima et al, 2010) is a sophisticated
deductive reasoning system based on SOL resolu-
tion (Inoue, 1992) and the connection tableaux, which
avoids producing non-minimal consequences as well
as redundant computation using state-of-the-art prun-
ing techniques. Consequence enumeration is a strong
point of SOLAR as an abductive procedure because
it enables us to compare many different hypotheses
(Inoue et al, 2009).
3 PARTITION-BASED
CONSEQUENCE FINDING
This section proposes partition-based consequence
finding. We start from a review of the basic termi-
nology and the message passing algorithm between
partitioned knowledge bases in (Amir et al, 2005),
whose basic idea is from Craig’s Interpolation The-
orem (Craig, 1957; Slagle, 1970).
3.1 Partitions and Message Passing
We suppose the whole axiom set A =
S
i≤n
A
i
, in
which each axiom set A
i
(i ≤ n) is called a partition.
We denote as S(A
i
) the set of (non-logical) symbols
appearing in A
i
. A graph induced from the partitions
S
i≤n
A
i
is a graph G = (V, E, l) such that (i) the set V
of nodes are the same as the partitions, that is, i ∈ V iff
the partition A
i
exists; (ii) the set E of edges are con-
structed as E = {(i, j) | S(A
i
) ∩ S(A
j
) 6=
/
0}, that is,
the edge (i, j) ∈ E iff there is a common symbol be-
tween A
i
and A
j
; and (iii) the mapping l determines
the label l(i, j) of each edge (i, j) called the com-
munication language between the partitions A
i
and
A
j
. In partition-based theorem proving by (Amir et
al, 2005), l(i, j) is initially set to the common lan-
guage of A
i
and A
j
, which is C(i, j) = S(A
i
) ∩ S(A
j
).
The communication language l(i, j) is then updated
by adding symbols from some other partitions when
cycles are broken (Algorithm 3.2). In Section 3.3,
l(i, j) is further extended by including the language
for consequence finding.
Given the partitions
S
i≤n
A
i
and its induced graph
G = (V, E, l), we now consider the query Q to be
proved in the partition A
k
(k ≤ n). Given a set S of
non-logical symbols, the set of formulas constructed
from the symbols in S is denoted as L (S).
Definition 3.1. For two nodes i,k ∈ V , the length of a
shortest path between i and k is denoted as dist(i, k).
Given k, we define i ≺
k
j if dist(i, k) < dist( j, k).
When k is clear from the context, we simply denote
i ≺ j instead of i ≺
k
j. For a node i ∈ V , a node j ∈ V
such that (i, j) ∈ E and j ≺
k
i is called a parent of i
(with respect to ≺
k
). In the ordering ≺
k
, the node k
is called the root (with respect to ≺
k
), and a node i
that is not a parent of any node is called a leaf (with
respect to ≺
k
).
Algorithm 3.1 (Message Passing). (Amir et al, 2005)
1. Determine ≺
k
according to Definition 3.1.
2. Perform consequence finding in each A
i
in paral-
lel. If A
k
|= Q, then return YES.
3. For every i, j ∈ V such that j is the parent of i, if
there is a consequence ϕ of the partition A
i
such
that ϕ ∈ L (l(i, j)), then add ϕ to the axiom set A
j
.
4. Repeat Steps 2 to 3 until no more new conse-
quence is found.
Algorithm 3.1 works well for theorem proving at
A
k
when the induced graph is a tree. However, if there
is a cycle, we need to break it to transform the graph
to a tree.
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
136

Algorithm 3.2 (Cycle Cut). (Amir et al, 2005)
1. Find a shortest cycle v
1
, . . . , v
c
(= v
1
) (v
i
∈ V ) in
G. If there is no cycle, return G.
2. Select a such that a < c and Σ
j<c, j6=a
| l(v
j
, v
j+1
)∪
l(v
a
, v
a+1
) | is smallest.
3. For every j < c, j 6= a, let l(v
j
, v
j+1
) :=
l(v
j
, v
j+1
) ∪ l(v
a
, v
a+1
).
4. Put E := E \{(v
a
, v
a+1
)} and l(v
a
, v
a+1
) :=
/
0, then
go to Step 1.
When there are multiple shortest cycles, common
edges should be removed. But if there is no common
edge, edges are removed so that the sum of the sizes
of communication languages becomes the smallest. It
is important to decide the order to remove edges al-
though any ordering results in a translation to a tree.
Cycle Cut Algorithm 3.2 is designed to minimize the
total size of the communication languages.
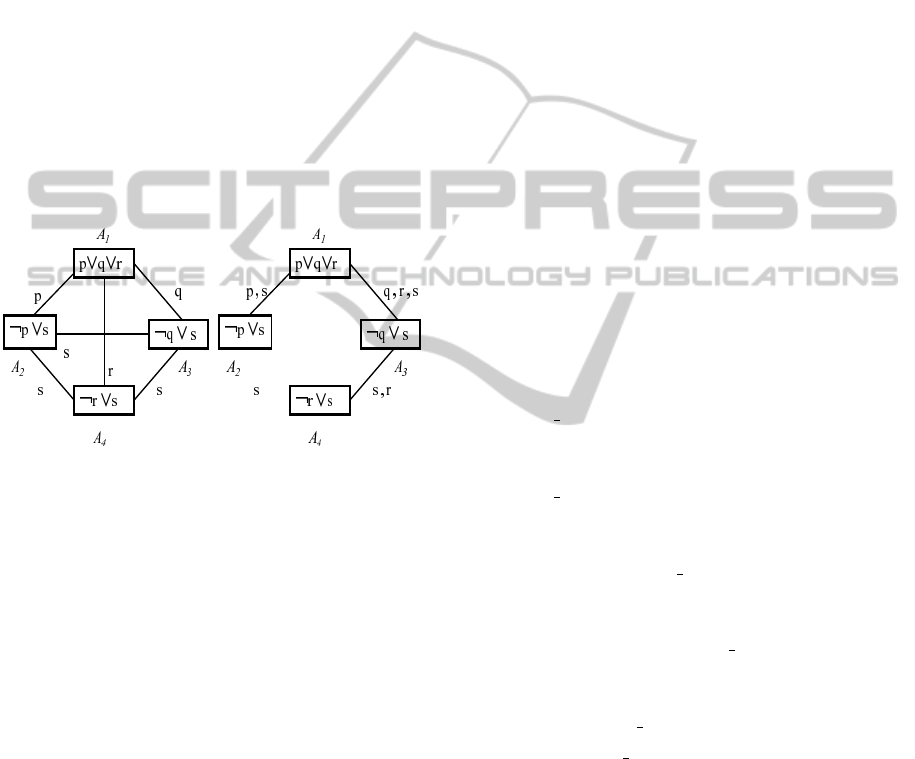
Figure 1: Translation of a cyclic graph to a tree (Amir et al,
2005).
Figure 1 shows an example of cycle cut. The left
figure is translated to the right figure. Firstly, the
shortest cycle (1,3), (3,4), (4,1) is considered, and
then the edge (4,1) is deleted. The communication
language of (4,1) is then added to those of (1,3) and
(3,4). Next, from the cycle (1,3), (3,2), (2,1), the edge
(3,2) is removed, and s is added to l(1, 3) and l(2, 1).
Then, the cycle (1,3), (3,4), (4,2), (2,1) is taken, and
the edge (4,2) is removed from it, but s is already
in l(3, 4) and l(4, 2). Now Algorithm 3.1 is applied;
¬p ∨ s is sent from A
2
to A
1
, deducing q ∨ r ∨ s (as
the resolvent of ¬p ∨ s and p ∨ q ∨ r), which is then
sent from A
1
to A
3
, deducing r ∨ s (as the resolvent
of q ∨ r ∨ s and ¬q ∨ s), which is sent from A
3
to A
4
.
Finally, the conclusion s is obtained at A
4
.
Theorem 3.1. (Amir et al, 2005). Suppose an ax-
iom set and its partitions A =
S
i≤n
A
i
and a formula
Q ∈ L (A
k
) (k ≤ n). If the consequence finding proce-
dure in each partition is sound and complete, apply-
ing Algorithm 3.2 and then Algorithm 3.1 returns YES
iff A |= Q.
Partition-based theorem proving of (Amir et al,
2005) cannot be directly applied to consequence find-
ing problems for Q 6∈ L (A
k
) although (Amir et al,
2005, Section 2.3) briefly mentions how to apply their
MP algorithm to such a query constructed from lan-
guages in different partitions (a more detailed discus-
sion will be given later in Section 3.3). Hence, we will
extend the partition-based reasoning framework to a
complete method for distributed consequence finding.
3.2 Example
We now show an example to see that the partition-
based theorem proving method cannot be directly ap-
plied to consequence finding. The problem is to find
means to withdraw money from one’s bank account.
The intended solution is that one must have either
a cash card or a bankbook, which is represented as
card ∨ bankbook. The knowledge base of this prob-
lem consists of the following clauses.
• ¬holiday ∨ closed (The bank is closed on holi-
days.)
• ¬weekday ∨ open (The bank is open on week-
days.)
• holiday ∨ weekday (Any day is either a holiday
or a week day.)
• ¬need money ∨ ¬open ∨ ATM ∨ counter (If one
needs money and the bank is open, then (s)he goes
to an ATM or a counter of the bank.)
• ¬need money ∨ ¬closed ∨ ATM (If one needs
money and the bank is closed, then (s)he goes to
an ATM.)
• ¬AT M ∨ card ∨ ¬get money (One cannot get
money if (s)he does not have a cash card at an
ATM.)
• ¬counter ∨bankbook ∨¬get money (One cannot
get money if (s)he does not have a bankbook at a
counter.)
• Input facts: need money (One needs money.)
• Input facts: get money (One gets money.)
Here we assume that the partitions are constructed
as in Fig. 2, in which clauses are distributed in a scat-
tered way. Algorithm 3.2 removes the edge (1,3) and
then adds AT M to the labels of other edges. How-
ever, the clause card ∨ bankbook cannot be deduced
by Message Passing Algorithm 3.1: since l(1, 2) and
l(1, 3) do not contain card, the clause (1) cannot be
resolved with any clause in other partitions. In fact, it
is necessary to resolve all clauses (1) to (7).
COMPLETE DISTRIBUTED CONSEQUENCE FINDING WITH MESSAGE PASSING
137

2010/6/13
1
get_money, need_money, holiday
counter, weekday,
get_money, need_money
ATM, get_money,
need_money
A 1 A 2
A 3
(1)!ATM!card !!get_money
(2)!need_money !!closed!ATM
(3)!holiday ! closed
(4) weekday ! holiday
(5) !counter ! bankbook !!get_money
(6) need_money
(7) !need_money ! !open ! ATM ! counter
(8) get_money
(9) !weekday ! open
A 1 A 2
A 3
(1)!ATM!card !!get_money
(2)!need_money !!closed!ATM
(3)!holiday ! closed
(4) weekday ! holiday
(5) !counter ! bankbook !!get_money
(6) need_money
(7) !need_money ! !open ! ATM ! counter
(8) get_money
(9) !weekday ! open
get_money, need_money, holiday,
ATM, card, bankbook
counter, weekday,
get_money, need_money,
ATM, card, bankbook
Figure 2: Partitions for “Getting Money”.
3.3 Partition-based Consequence
Finding
We here propose a new method to construct the com-
munication language so that Message Passing Algo-
rithm can be made complete for consequence finding.
Suppose the whole axiom set and its partitions
A =
S
i≤n
A
i
. Recall that the common language of
A
i
and A
j
is C(i, j) = S(A
i
) ∩ S(A
j
) (i, j ≤ n i 6=
j). Here, we construct the communication language
l(i, j) between A
i
and A
j
for consequence finding by
extending C(i, j). Let P = hLi be the given produc-
tion field. By adding the literals appearing in L to the
common language, each communication language in
the case of trees is defined as
l(i, j) = C(i, j) ∪ S(L). (3)
When there are cycles in the graph G, the final com-
munication language is set after all cycles are cut us-
ing Algorithm 3.2. For example, suppose that an edge
(s, r) is removed from a cycle. Then, the communica-
tion language of an edge (i, j)(6= (s, r)) in the cycle is
defined in the same way as before:
l(i, j) = C(i, j) ∪ l(s, r) ∪ S(L). (4)
Two remarks are noted here. Firstly, in (3) and (4),
the polarity of each literal in L from the production
field P are lost within the symbols S(L). Although
this does not harm soundness and completeness of
distributed consequence finding, there is some redun-
dancy in communication. Then, unlike the case of
common language C(i, j), we can keep the polarity
of each literal in L in any l(i, j) so that unnecessary
clauses possessing literals that do not belong to P are
not communicated between partitions. Second, when
C(i, j) =
/
0 the edge (i, j) does not exist in the graph
G. In this case, l(i, j) need not be updated as S(L) us-
ing (3) and actually the edge is kept unnecessary. In
fact, if we could add the literals from the production
field to those non-existent edges in G, then the result-
ing graph G
0
would become strongly connected. By
applying Cycle Cut Algorithm 3.2 to G
0
, the minimal
way is to cut those added edges again. However, other
edges already have the literals S(L) so their commu-
nication languages do not change. Hence, we do not
have to reconsider non-existent edges in G.
Algorithm 3.3 (Partition-based Consequence Find-
ing).
1. If there is a cycle in the induced graph G, select
some k ≤ n and apply Cycle Cut Algorithm 3.2 to
G and transform it to a tree.
2. Determine the communication language between
all pairs of partitions. For each leaf partition A
i
,
do the following.
3. If A
i
is the root partition, let P
i
be the original
production field P = hLi. Otherwise, let j be the
parent of i, and define the production field of A
i
as P
i
= hl(i, j)
±
i, where l(i, j)
±
is the set of liter-
als constructed from l(i, j). Perform consequence
finding in A
i
with the production field P
i
, and let
Cn
i
:= Carc(A
i
, P
i
). Output each characteristic
clause C ∈ Cn
i
if C belongs to the original pro-
duction field P = hLi.
4. For each clause C ∈ Cn
i
, check if C ∈ L (l(i, j)).
If so, send C to A
j
and let A
j
:= µ(A
j
∪ {C}). Put
i := j.
5. As long as there is a clause to be sent to the parent
partition, repeat Steps 3 to 5.
Step 1 in Algorithm 3.3 can be run in parallel for
each partition that is most distant from the root par-
tition. Step 4 can be computed in parallel for each
characteristic clause.
For the example in Section 3.2, applying Cycle
Cut and the decision method of the communication
language results in Fig. 3. By this way, the clause (1)
consists of the symbols in l(1, 2), then can be resolved
with other clauses in A
2
. Applying Algorithm 3.3,
the intended consequence card ∨bankbook can be ob-
tained.
2010/6/13
1
get_money, need_money, holiday
counter, weekday,
get_money, need_money
ATM, get_money,
need_money
A 1 A 2
A 3
(1)!ATM!card !!get_money
(2)!need_money !!closed!ATM
(3)!holiday ! closed
(4) weekday ! holiday
(5) !counter ! bankbook !!get_money
(6) need_money
(7) !need_money ! !open ! ATM ! counter
(8) get_money
(9) !weekday ! open
A 1 A 2
A 3
(1)!ATM!card !!get_money
(2)!need_money !!closed!ATM
(3)!holiday ! closed
(4) weekday ! holiday
(5) !counter ! bankbook !!get_money
(6) need_money
(7) !need_money ! !open ! ATM ! counter
(8) get_money
(9) !weekday ! open
get_money, need_money, holiday,
ATM, card, bankbook
counter, weekday,
get_money, need_money,
ATM, card, bankbook
Figure 3: Updating Communication Languages.
Termination of Algorithm 3.3 is guaranteed under
some finiteness conditions. For this, (1) if there is
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
138

a finite number of cycles in the induced graphs, the
maximum depth of a tree is finite after applying Al-
gorithm 3.2, and (2) if there are no recursive theories
in each partition, consequence finding in the partition
produces a finite number of characteristic clauses.
The second condition is satisfied if ground conse-
quences are only produced and there are no function
symbols in the language.
The correctness of a distributed consequence find-
ing algorithm A is defined as follows. Suppose the
whole knowledge base A and a production field P . A
is sound if any clause derived by A is a logical con-
sequence of A and belongs to P . A is complete if it
holds for any partitioning of A that: for any clause C
belonging to T h
P
(A), there is a clause D derived by
A such that D subsumes C.
Theorem 3.2. (Soundness and Completeness of
Partition-based Consequence Finding). Suppose
an axiom set and its partitions A =
S
i≤n
A
i
, its in-
duced graph G = (V, E, l), and a stable production
field P = hLi. We assume that every partition A
i
has a
sound and complete algorithm for consequence find-
ing. Then, Algorithm 3.3 is sound and complete for
distributed consequence finding.
Proof. Any clause derived by Algorithm 3.3 refers to
a subset of A and belongs to P . Then, soundness fol-
lows from the monotonicity of first-order logic. Com-
pleteness can be proved by induction on the length
of any clause C ∈ T h
P
(A). When |C| = 1, let A
k
be a partition of A such that C ∈ L(A
k
). Then, by
Theorem 3.1, a clause D subsuming C can be de-
rived by Algorithm 3.3, which works in the same way
as Algorithm 3.1. Suppose that completeness holds
for |C| ≤ m, and we prove the case of |C| = m + 1.
Let C = C
0
∨ L, where |C
0
| = m and L is a literal.
Let A
0
be A ∪ {¬L}. Since C
0
belongs to P and
C ∈ T h
P
(A), C
0
∈ T h
P
(A
0
) holds. Then, assume a
partition A
0
=
S
i≤n
A
0
i
where A
0
j
= A
j
for j 6= k and
A
0
k
= A
k
∪ {¬L} for some k ≤ n. By induction hy-
pothesis, a clause D
0
subsuming C
0
can be derived
from A
0
at A
0
k
by Algorithm 3.3. In fact, if D
0
is de-
rived at some A
0
j
( j 6= k), then it can be sent to A
0
k
because D
0
belongs to P and hence D
0
∈ L (l( j, k)).
We now construct a distributed proof of a clause D
subsuming C from A by adding L to C
0
appearing in
the distributed proof of D
0
from A
0
. This is possible
because L ∈ L (l(i, j)) for any i, j ∈V by the construc-
tions (3) and (4). Hence, D can be derived at A
k
by
Algorithm 3.3.
Algorithm 3.3 can be seen as a simple extension of
partition-based theorem proving by Amir and McIl-
raith (Amir et al, 2005) since the communication lan-
guages are extended to include the literals from the
production field. However, this small change is es-
sential for consequence finding. For theorem proving,
Amir and McIlraith (Amir et al, 2005, Section 2.3)
have mentioned how to deal with a query Q that com-
prises symbols drawn from multiple partitions. For
this, a new partition A
Q
is added with the language
S(A
Q
) = S(Q) and A
Q
consists of the clausal form of
¬Q. Following addition of this new partition, Cycle
Cut must be run on the new graph, and then refutation
is performed at A
Q
. This method, however, cannot be
elegantly applied for consequence finding in general
since we do not know the exact theorems or even the
possible candidates of theorems to be found in conse-
quence finding. Of course, we can consider the pro-
duction field P = hLi for restricted consequence find-
ing. But even with a small P , say L = {a, b, c}, to
find all consequences with theorem proving we need
to query for a, b, c, then possibly a ∨ b, a ∨ c and
b∨c, and eventually a∨b∨c (though querying the last
clause a∨b∨c and checking all possible proofs would
also work but have high complexity too). Alterna-
tively, considering the new partition A
P
with the lan-
guage S(L) makes the graph more tightly connected
and cyclic. Applying Cycle Cut would then modify
the communication language of an existing edge to
include S(L), which has a similar effect as the equa-
tion (3).
Another important change from the MP algorithm
by Amir and McIlraith (Amir et al, 2005) is to use
the production field P
i
= hl(i, j)
±
i in Step 3 of Al-
gorithm 3.3 for consequence finding. This limits the
computations that need to be done and thus improves
efficiency. The use of production fields also enables
us to emulate default reasoning by adding each de-
fault literal in a production field to be skipped (Inoue
et al, 2004; Inoue et al, 2006). Hence, our algorithm
can be extended to partition-based default reasoning.
4 COOPERATIVE
CONSEQUENCE FINDING
Partition-based distributed consequence finding is
particularly useful when we have a large knowledge
base that should be divided to easily handle each piece
of knowledge. However, the algorithm can also be
applied to naturally distributed knowledge-based sys-
tems in which each theory of an agent grows individu-
ally so that multiple agents may have the same knowl-
edge and information simultaneously. Although such
possessed knowledge is considered to be redundant
in partition-based theories, there is no problem in
decentralized, multi-agent and peer-to-peer systems.
COMPLETE DISTRIBUTED CONSEQUENCE FINDING WITH MESSAGE PASSING
139

In such naturally distributed systems, one problem
would be to break cycles in the induced graph because
no agent should know an optimal way to minimize the
cost of cutting cycles (although we could devise a de-
centralized version of Cycle Cut algorithm).
In this section, we thus consider an alternative ap-
proach to distributed consequence finding that is suit-
able for such autonomous agent systems. The new
method is more cooperative than the previous one in
the sense that agents are always seeking other agents
who can accept new consequences for further infer-
ence. In this method, we do not presuppose network
structures of agents, but any agent can have a chance
to communicate with other agents. As the language
and knowledge of each agent evolves through interac-
tions, this framework is more dynamic than the first
method. Since the method is not partition-based, we
do not call each distributed component a partition, but
call it an agent in this section.
Algorithm 4.1 (Cooperative Consequence Finding).
1. Suppose a set I of input clauses is given. This
consists of a query or a goal clause in the case
of query answering or abduction as well as any
clause input to the whole system A . Let A
i
be a newly created agent whose axiom set is I.
Let P
A
= hLit
A
i be the (stable) production field,
where Lit
A
is the set of all literals in the language
of A . Perform consequence finding in A
i
, and let
N := Carc(A
i
, P
A
).
2. For each clause C ∈ N, decide an agent A
j
to
which C is sent from A
i
. Put i := j.
3. In A
i
, consequence finding is performed by SOL
resolution with the top clause C. Let N :=
Newcarc(A
i
,C, P
A
). Put A
i
:= µ(A
i
∪ N).
4. Repeat Steps 2 to 3 until no more new character-
istic clause is derived.
Algorithm 4.1 repeats the process of (a) and (b):
(a) new consequences obtained in an agent are sent to
others, and (b) then they trigger consequence finding
in those agents. An advantage of this method is that
we only need to compute new characteristic clauses
Newcarc(A
i
,C, P
A
) in Step 3. In fact, computation of
new characteristic clauses is easier than computation
of the whole characteristic clauses by SOL resolution.
The whole characteristic clauses are still obtained by
accumulating the new ones with subsumption check-
ing by simulating (1) and (2) in Step 3. Note that
computation of Carc(A
i
, P
A
) in Step 1 is not neces-
sary when I is a single clause or contains no compli-
mentary literals.
In Step 2 of Algorithm 4.1, we assume that any
agent can decide to which agent each clause C ∈ N
should be sent. One such implementation is to as-
sociate with each agent A
i
the set of predicates with
their polarities appearing in the axiom set. This set
must be updated each time a new characteristic clause
is computed in the agent. Then, it becomes easier to
find a literal that is complementary to a literal in C
in other agents. One can also use the current com-
munication language l(i, j) between two agents: if
C ∩ l(i, j) 6=
/
0 holds, then C can be sent from A
i
to
A
j
. Note here that we do not need to break cycles,
but l(i, j) needs to be updated whenever the axioms
are updated. In another way, a blackboard architec-
ture like (Ciampolini et al, 2003) can be considered
as a place to store new characteristic clauses deduced
by agents. An agent should check whether it has a
clause which can be resolved with a new characteris-
tic clause.
2010/6/13
1
(6)
A 1 A 2
A 3
(1)!ATM!card !!get_money
(2)!need_money !!closed!ATM
(3)!holiday ! closed
(4) weekday ! holiday
(5) !counter ! bankbook !!get_money
(6) need_money
(7) !need_money ! !open ! ATM ! counter
(8) get_money
(9) !weekday ! open
(6)
(8)
(8)
Figure 4: First Message Passing in Cooperative Conse-
quence Finding (arrows indicates message passing, labelled
by the number of the sent clause, and the complementary
pair of literals causing the sending is also emphasized).
Note that implementation of Steps 2 to 4 can be
parallelized provided that synchronization is properly
done. The first message passing for unit clauses is
illustrated in Fig. 4 for the example of Section 3.2.
Termination of Algorithm 4.1 is similar to the
case of Algorithm 3.3. For the correctness of Algo-
rithm 4.1, the following theorem holds.
Theorem 4.1. (Soundness and Completeness of
Cooperative Consequence Finding). Suppose an
axiom set and its partitions A =
S
i≤n
A
i
. We assume
that every agent A
i
has a sound and complete algo-
rithm for consequence finding. Then, Algorithm 4.1 is
sound and complete for distributed consequence find-
ing of Newcarc(A, I, P
A
).
Proof. Soundness is proved in the same way as Theo-
rem 3.2. For completeness, Newcarc(A, I, A
P
) can be
decomposed into multiple clause-by-clause Newcarc
operations by (1). Since we use the production field
P
A
in which all literals appearing in A can be skipped,
all Skip operations in any SOL deduction from the
whole A are also applied by Algorithm 4.1. On the
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
140

other hand, all Resolve operations of SOL deduc-
tions can be simulated by sending resolving clauses
to other agents. Ancestor resolution in SOL deduc-
tions can also be done by sending back to previous
agents. Thus, any SOL deduction can be simulated in
a distributed setting by 4.1.
5 COMPARING APPROACHES
We here compare the two proposed methods for dis-
tributed consequence finding. We first note that
the two methods are not designed to compute the
same consequences as long as Theorems 3.2 and 4.1
are concerned. Given an axiom set A , partition-
based consequence finding computes Carc(A , P ) be-
longing to a given production field P in Theo-
rem 3.2, while cooperative consequence finding com-
putes Newcarc(A, I, P
A
) for a given set of inputs I in
Theorem 4.1. We could extend both methods to deal
with any case by considering the same conditions for
them. However, the current conditions are natural in
both methods. The partition-based approach is based
on Interpolation Theorem (Craig, 1957), which refers
to the set of consequences of an axiom set of one par-
tition, yet a language restriction can be used effec-
tively. On the other hand, the cooperative approach is
more dynamic and reflective so that ramification from
the new input is propagated to other agents, but the
language restriction is not easily set since every agent
could be related to any other. Nevertheless, an obvi-
ous merit of the cooperative method is that we do not
need to break cycles.
Then, we consider the situation that Algo-
rithms 3.3 and 4.1 can be fairly compared. In the
example in Section 3.2, we have two input clauses
from the world as I and the production field can be
set to P
A
. Here we compare the number of resolu-
tion steps as well as the number of sent messages in
solving this example. For comparison, we also show
the results of the centralized approach. As the conse-
quence finding system in each partition or agent, SO-
LAR (Nabeshima et al, 2003) is used. The ordering or
partitions in the partition-based consequence finding
is set to A
1
→ A
2
→ A
3
.
Table 1 (a) shows the number of resolution steps
in each method. Comparing two distributed methods
with the centralized one, the total number of resolu-
tion steps becomes fewer in both methods. This is be-
cause (i) the partition-based method restricts clauses
sent to its parent to those constructed with the com-
munication language between those partitions and (ii)
the cooperative method performs consequence find-
ing in each agent only with top clauses sent from other
Table 1: Comparison of three methods for “Getting
Money”(Okamoto et al, 2005).
(a) # resolution steps (b) # sent messages
Approach
A
1
A
2
A
3
total A
1
A
2
A
3
total
Centralized – – – 659 – – – 0
Partition-based 19 51 461 531 3 5 0 8
Cooperative 27 62 63 152 5 7 8 20
agents. Comparing the partition-based method with
the cooperative one, we see that the latter is more
uniformly distributed in its load balance. The for-
mer, partition-based one, has the property that the
number of inference steps becomes increasing from
leaves to the root. In a leaf partition, there are fewer
axioms and thus the number of resolution steps is
fewer too. Sending messages from descendants to
ancestors, more and more clauses are gathered so
that more resolution steps become necessary at later
stages. Then, the bottom partition mostly collects
clauses from the descendants. As a result, the load
balance of the partition-based method is not averaged.
On the other hand, the cooperative method send newly
obtained consequences to all agents that have resolv-
able clauses, which prevents overloads in particular
agents. In the example, agents efficiently cooperate
with each other to get the final consequence.
Table 1 (b) shows a comparison between the
partition-based and the cooperative methods on the
number of messages sent to other partitions. Each
message corresponds to one clause in this compari-
son. In the partition-based method, all cycles in the
graph are broken, and message passing is done from
leaves to the root in only one way. Any message is
thus sent to the parent only once. On the other hand,
the cooperative method sends messages to all agents
possessing resolvable clauses, which increases the
number of communications between agents. If there
are many agents containing clauses that can be re-
solved with a consequence of some agent, the number
of messages to be sent in the cooperative method be-
comes larger than that of the partition-based method.
6 RELATED WORK
Consequence finding has been investigated in a dis-
tributed setting (Inoue et al, 2004; Amir et al, 2005;
Adjiman et al, 2005). Inoue and Iwanuma (Inoue
et al, 2004) consider a multi-agent framework which
performs speculative computation under incomplete
communication environments. This is a master-
slave style multi-agent system, in which a master
agent asks queries to slave agents in problem solv-
ing and proceeds computation with default answers
when answers from slave agents are delayed. Spec-
COMPLETE DISTRIBUTED CONSEQUENCE FINDING WITH MESSAGE PASSING
141

ulative computation is implemented with SOL res-
olution with the conditional answer method to up-
date agents’ beliefs according to situation changes.
On the other hand, distributed consequence finding in
this paper does not assume any master agent to con-
trol the whole system. Amir and McIlraith (Amir et
al, 2005) propose distributed theorem proving to im-
prove the efficiency of theorem proving for structured
theories. Their message-passing algorithm reasons
over these theories using consequence-finding, and
our first (partition-based) approach in this paper also
uses it. As already stated in Section 3.3, the main dif-
ference between (Amir et al, 2005) and our partition-
based approach is that the goal of the former is the-
orem proving while our goal is consequence finding.
Another difference is that (Amir et al, 2005) consid-
ers how to partition a problem to minimize the inter-
section of the languages, while we suppose the situa-
tion that such optimal partitioning cannot be applied
because of inherent distribution of knowledge and im-
possibility to collect all information to one place. This
last observation directed us to the second, cooperative
approach to distributed consequence finding, which is
quite different from the first one.
The peer-to-peer (P2P) consequence finding sys-
tem proposed by Adjiman et al. (Adjiman et al, 2005;
Adjiman et al, 2006) is perhaps closest to our work.
Their method is related to our both first (partition-
based) and second (cooperative) approaches to con-
sequence finding. (Adjiman et al, 2005) composes
an acquaintance graph from the peers using informa-
tion of shared symbols, which is similar to a graph
induced from the partitions in our first approach. The
difference is that (Adjiman et al, 2005) does not break
cycles in a graph while we do. Also, (Adjiman et al,
2005) performs case splitting in goal-oriented reason-
ing of a peer P
1
by sending to other peer P
2
only those
subgoals contained in the shared symbols between P
1
and P
2
, then the new consequences of P
2
are returned
to P
1
, which is then composed in P
1
by replacing the
subgoal. Combining the results derived from the sub-
goals often would result in a huge combination of
clauses when the length of the goal is long, yet (Adji-
man et al, 2006) analyzes the scalability of large P2P
systems. On the other hand, we send the clause itself
without splitting and no re-collection is made. Our
second approach can be regarded as a dynamic ver-
sion of the first approach, in which messages are sent
whenever new clauses are derived, and there is no pre-
supposed network structures of agents. Such dynamic
aspects are not seen in the P2P setting. Another differ-
ence is that (Adjiman et al, 2005) can only deal with
propositional knowledge bases, while SOL resolution
and SOLAR in our paper can be used for consequence
finding in first-order clausal theories.
Although not in the context of consequence find-
ing, abduction has also been considered in a dis-
tributed setting. Since abduction in clausal theo-
ries can be implemented with consequence finding,
such work is somehow related to distributed conse-
quence finding. Greco (Greco, 2007) considers how
to build joint explanations from multiple agents in a
P2P setting like (Adjiman et al, 2005), but incorpo-
rates preference handling to have an agreement be-
tween agents. By extending a blackboard architecture
of (Ciampolini et al, 2003), Ma et al. (Ma et al, 2008)
address distribution of abductive logic programming
agents by allowing agents to enter and exit proofs
done by other agents. Those works do not use conse-
quence finding, and communication between agents
are fully guaranteed. More recently, Bourgne et al.
(Bourgne et al, 2010) propose the learner-critique
approach in which the role of each agent dynami-
cally changes between a generator and a tester of hy-
potheses when each agent never knows which sym-
bols are shared with other agents. In our methods, all
agents work uniformly as a reflective inference sys-
tem that derives consequences upon input of new for-
mulas, although shared symbols are assumed to be
known to both agents. Fisher (Fisher, 2000) shows
that certain forms of negotiation can be characterized
by distributed theorem proving in which agents act
as theorem-proving components. Analogously, dis-
tributed consequence finding might contribute to ex-
tended types of negotiation between agents.
In this work, we have focused on distributed rea-
soning systems in which a clause set is partitioned and
the common symbols between partitions are associ-
ated with links. In contrast, there is another formal-
ization of distribution in which variables or symbols
are partitioned and clauses containing symbols from
different partitions are associated with links between
those partitions. The former formalization is called
clause-set partitioned distribution, while the latter
is called variable-set partitioned distribution. Most
works on distributed constraint satisfaction problems
(DCSP) are based on the latter formalization (Yokoo
et al, 1998; Hirayama et al, 2005). These two for-
malizations can be converted into each other in the
propositional case (cf., (Dechter et al, 1989)), yet the
effect of the latter is unknown for consequence find-
ing while the former often occurs in real cases.
7 CONCLUSIONS
In this paper, we have proposed the two complete ap-
proaches for distributed consequence finding. The
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
142

first one extends the method of partition-based the-
orem proving in a suitable way, and the second one is
a more cooperative method for inherently distributed
systems. This paper rather focuses on complete-
ness of inference systems, and both approaches have
merits and demerits. Partition-based approaches can
utilize communication languages to realize restricted
consequence finding between the partitions, while the
cooperative approach does not need Cycle Cut al-
gorithm. On the negative side, it is important to
determine an appropriate ordering in the partition-
based method, while the number of messages sent be-
tween agents tends to become larger in the cooper-
ative approach. We could consider a third approach
by inheriting the merits of both approaches, such that
each agent is autonomous and cooperates each other
like the cooperative approach, yet each consequence
finder incorporates production fields and communica-
tion languages between agents to enhance efficiency.
Consideration of such a new approach is left as an
important future work. Another future task includes
more experiments with large distributed knowledge
bases by refining details of two algorithms and by
changing topological properties of agent links. More
comparison with P2P consequence finding (Adjiman
et al, 2006) is also necessary.
REFERENCES
Adjiman, P., Chatalic, P., Goasdou
´
e, F., Rousset, M.-C. and
Simon, L. (2005). Scalability study of peer-to-peer
consequence finding. In Proc. IJCAI-05, pp.351–356.
Adjiman, P., Chatalic, P., Goasdou
´
e, F., Rousset, M.-C. and
Simon, L. (2006). Distributed reasoning in a peer-to-
peer setting: Application to the semantic web. In J.
Artif. Intell. Res., 25:269–314.
Amir, A. and McIlraith, S. (2005). Partition-based logical
reasoning for first-order and propositional theories. In
Artif. Intell., 162:49–88.
Bourgne, G., Maudet, N., and Inoue, K. (2010). Abduction
of distributed theories through local interactions. In
Proc. ECAI’10, 901–906.
Ciampolini, A., Lamma, E., Mello, P., Toni, F., and Torroni,
P. (2003). Cooperation and competition in ALIAS: A
logic framework for agents that negotiate. Ann. Math.
Artif. Intell., 37(1-2):65–91.
Craig, W. (1957). Linear reasoning: A new form of
the Herbrand-Gentzen theorem. J. Symbolic Logic,
22:250–268.
Dechter, R. and Pearl, J. (1989). Tree clustering for con-
straint networks. Artif. Intell., 38:353–366.
del Val, A. (1999). A new method for consequence find-
ing and compilation in restricted languages. In Proc.
AAAI-99, pp.259–264.
Fisher, M. (2000) Characterizing simple negotiation as dis-
tributed agent-based theorem-proving—a preliminary
report. in: Proc. 4th ICMAS, pp. 127–134.
Greco, G. (2007). Solving abduction by computing joint ex-
planations. Ann. Math. Art. Intel., 50(1–2):143–194.
Hirayama, K. and Yokoo, M. (2005). The distributed break-
out algorithms. Artif. Intell., 161:89–115.
Inoue, K. (1992). Linear resolution for consequence find-
ing. Artif. Intell, 56:301–353.
Inoue, K. (2004). Induction as consequence finding. Ma-
chine Learning, 55:109–135.
Inoue, K. and Iwanuma, K. (2004). Speculative computa-
tion through consequence-finding in multi-agent envi-
ronments, Ann. Math. Artif. Intell., 42(1–3):255–291.
Inoue, K., Iwanuma, K. and Nabeshima, H. (2006). Conse-
quence finding and computing answers with defaults.
J. Intell. Inform. Systems, 26:41–58.
Inoue, K., Sato, T., Ishihata, M., Kameya, Y. and
Nabeshima, H. (2009). Evaluating abductive hypothe-
ses using an EM algorithm on BDDs. IJCAI, 810–815.
Iwanuma, K. and Inoue, K. (2002). Minimal answer com-
putation and SOL. JELIA ’02, LNAI 2424, 245–257,
Springer.
Lee, C.T. (1967). A completeness theorem and computer
program for finding theorems derivable from given
axioms. Ph.D. thesis, Department of Electrical En-
gineering and Computer Science, University of Cali-
fornia, Berkeley, CA.
Ma, J., Russo, A., Broda, K., and Clark, K. (2008). DARE:
A system for distributed abductive reasoning. AA-
MAS’08, 16(3):271–297.
Marquis, P. (2000). Consequence finding algorithms. in:
Handbook for Defeasible Reasoning and Uncertain
Management Systems, Vol. 5, pp.41–145, Kluwer.
Nabeshima, H., Iwanuma, K. and Inoue, K. (2003). SO-
LAR: A consequence finding system for advanced
reasoning. TABLEAUX, LNAI 2796, 257–263,
Springer.
Nabeshima, H., Iwanuma, K., Inoue, K. and Ray, O. (2010).
SOLAR: An automated deduction system for conse-
quence finding. AI Communic., 23(2–3):183–203.
Nienhuys-Cheng, S.-H. and de Wolf, R. (1997). Founda-
tions of Inductive Logic Programming. LNAI 1228,
Springer.
Okamoto, T., Inoue, K. (2005). Distributed consequence
finding with message communication. IPSJ-SIG Tech.
Rep., 24:25–30, (in Japanese).
Slagle, J.R. (1970). Interpolation theorems for resolution in
lower predicate calculus. J. ACM, 17(3):535–542.
Yokoo, M., Durfee, E.H., Ishida, T., and Kuwabara, K.
(1998). The distributed constraint satisfaction prob-
lem: Formalization and algorithms. IEEE Trans.
Know. & Data Eng., 10(5):673–685.
COMPLETE DISTRIBUTED CONSEQUENCE FINDING WITH MESSAGE PASSING
143