COMPARISON OF LINEAR CLASSIFICATION METHODS FOR

P300 BRAIN-COMPUTER INTERFACE ON DISABLED SUBJECTS

Nikolay V. Manyakov, Nikolay Chumerin, Adrien Combaz and Marc M. Van Hulle

Laboratory for Neuro- and Psychofysiology, K.U.Leuven, Herestraat 49, POBox 1021, 3000 Leuven, Belgium

Keywords:

Brain-computer interface, P300, Linear classiﬁer, Classiﬁcation accuracy, Amyotrophic lateral sclerosis, Mid-

dle cerebral artery stroke, Subarachnoid hemorrhage.

Abstract:

In this paper, we investigate the accuracy of linear classiﬁcation techniques for a P300 Brain-Computer Inter-

face used in a typing paradigm. Fisher’s Linear Discriminant Analysis (LDA), Bayesian Linear Discriminant

Analysis (BLDA), Stepwise Linear Discriminant Analysis (SLDA), linear Support Vector Machine (SVM)

and a method based on Feature Extraction (FE) were compared. Experiments were performed on patients

suffering from Amyotrophic Lateral Sclerosis (ALS), middle cerebral artery (MCA) stroke and Subarachnoid

Hemorrhage (SAH), in on-line and off-line mode. Our results show that BLDA yields a signiﬁcantly higher

accuracy than the other linear techniques we have compared, at least for our group of subjects.

1 INTRODUCTION

Research on brain-computer interfaces (BCIs) has

witnessed a tremendous development in recent years

(Sajda et al., 2008), and has enjoyed much attention

even in popular media. Although a lot of research

was done on invasive BCIs, leading to brain implants

decoding neural activity directly, which are primarily

tested on animals, noninvasive BCIs, e.g., based on

electroencephalograms (EEG) recorded on the sub-

ject’s scalp, have recently enjoyed an increasing at-

tention since they do not require any surgical pro-

cedure, and can therefore be more easily tested on

human subjects. Several noninvasive BCI paradigm

have been described in the literature, but the one we

concentrate on, relies on the event-related potential

(ERP, a stereotyped electrophysiological response to

an internal or external stimulus (Luck, 2005)).

One of the most explored ERPs is the P300. It can

be detected while the subject is shown two types of

events with one occurring much less frequently than

the other (”rare event”). The rare event elicits an ERP

consisting of an enhanced positive-going signal com-

ponent with a latency of about 300 ms after stimulus

onset (Luck, 2005). In order to detect the ERP, the

recording of one trial is usually not enough, and the

recordings of several trials need to be averaged. Aver-

aging is required because the recorded signal is a su-

perposition of the activity related to the stimulus and

all other ongoing brain activity. By averaging, the ac-

tivity that is time-locked to a known event (e.g., the

onset of the attended stimulus) is extracted as an ERP,

whereas the activity that is not related to the stimu-

lus onset is expected to be averaged out. The stronger

the ERP signal, the fewer trials are needed, and vice

versa.

There has been a growing interest in the ERP de-

tection problem, as witnessed by the increased avail-

ability of BCIs that rely on ERP detection. A noto-

rious example is the P300 mind-typer (Farwell and

Donchin, 1988), and with which subjects are able to

type words and sentences on a computer screen. This

application meets the BCI’s primary goal, namely, to

improve the quality of life of neurologically impaired

patients suffering from pathologies such as: amy-

otrophic lateral sclerosis, brain stroke, brain/spinal

cord injury, cerebral palsy, muscular dystrophy, etc.

But, as is mostly the case with BCI research, they

have been tested primarily on healthy subjects. Only

very few attempts have been made on patients (Ni-

jboer et al., 2008; Sellers and Donchin, 2006; Pic-

cione et al., 2006; Hoffmann et al., 2008; Silvoni

et al., 2009; Sellers et al., 2010). Several of these

patient tests (Nijboer et al., 2008; Sellers et al., 2010)

deal with P300-based on-line typing, however, since

only very few patients were tested, it is still must be

investigated whether the P300 mind-typer is suited for

them.

In addition, studies that report on the perfor-

mance of different P300 classiﬁers were only made

328

V. Manyakov N., Chumerin N., Combaz A. and M. Van Hulle M..

COMPARISON OF LINEAR CLASSIFICATION METHODS FOR P300 BRAIN-COMPUTER INTERFACE ON DISABLED SUBJECTS.

DOI: 10.5220/0003273903280334

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2011), pages 328-334

ISBN: 978-989-8425-35-5

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

for healthy subjects. It, thus, remains to be seen how

the comparison will look like for disabled subjects,

and how this will affect the choice of the best classi-

ﬁer. This is indeed an important question since the

P300 responses from healthy subjects and disabled

patients can be quite different (Sellers and Donchin,

2006). Thus, the results of the classiﬁcation perfor-

mance comparison for healthy subjects could possi-

bly not be valid for disabled ones. In addition, the

outcomes of the comparison, performed on healthy

subjects, also lead to slightly different conclusions.

In (Krusienski et al., 2006) a comparison of several

classiﬁers (Pearson’s correlation method, Fisher’s lin-

ear discriminant analysis (LDA), stepwise linear dis-

criminant analysis (SLDA), linear support-vector ma-

chine (SVM) and Gaussian kernel support vector ma-

chine) was performed on 8 healthy subjects. It was

shown that SLDA and linear SVM render the best

overall performance. In (Mirghasemi et al., 2006) it

was shown that, among linear SVM, Gaussian kernel

SVM, multi-layer perceptron, LDA and kernel LDA,

the best performance was achieved by LDA. Based on

these studies, albeit different sets of classiﬁers were

used in the comparison, one can conclude that lin-

ear classiﬁers work better than nonlinear ones, at least

for the P300 BCI. This statement is also supported by

other researchers (e.g., in (Lotte et al., 2007)).

Figure 1: Typing matrix of the Mind Speller. Rows and

columns are ﬂashed in random order; one trial consists of

ﬂashing all six rows and all six columns. The intensiﬁcation

of the third column (left panel) and the second row (right

panel) are shown.

In this paper, we report on tests performed on

a group of partially disabled patients suffering from

Amyotrophic Lateral Sclerosis (ALS), Middle Cere-

bral Artery (MCA) stroke, and Subarachnoid Hemor-

rhage (SAH). We compare several linear techniques

for P300 BCI classiﬁcation. In addition to the linear

techniques mentioned above, we also add two more

methods (i.e., Bayesian linear discriminant analysis

and a method based on feature extraction). Thus, in

our study we compare a much more extensive set of

linear classiﬁcation techniques, and perform our com-

parison on disabled patients, instead of healthy sub-

jects, both of which distinguishes our approach from

others.

2 METHODS

2.1 EEG Data Acquisition

The EEG recordings were performed using a proto-

type of an ultra low-power 8-channels wireless EEG

system. The wireless EEG system was developed

by IMEC

and built around their ultra-low power 8-

channel EEG ampliﬁer chip (Yazicioglu et al., 2006).

The data are transmitted with a sampling frequency

of 1000 Hz for each channel. We used a brain-cap

with large ﬁlling holes and sockets for activeAg/AgCl

electrodes (ActiCap, Brain Products). The recordings

were made with eight electrodes located primarily on

the parietal pole, namely at positions Cz, CPz, P1, Pz,

P2, PO3, POz, PO4, according to the international

10–20 system. The reference electrode and ground

were placed on the left and right mastoids.

2.2 Experiment Design

Twelve subjects, na¨ıve to BCI applications, partici-

pated in the experiments (ten male and two female,

aged 37–66 with an average age of 51.25). The sub-

jects were suffering from different types of brain dis-

orders. The experimental protocol was approved by

the ethical committee. After the recordings were

made, four subjects were excluded from further clas-

siﬁer comparison, since their performance was close

to chance level, which could be due to the nature of

their brain disorder or because they did not understand

the experiment. The information about the patients

(EEG data of which where used for the analysis) in-

cluding their diagnoses, age and gender is presented

in Table 1.

We have used the same visual stimulus paradigm

as the one used in the ﬁrst P300-based speller, which

was introduced by Farwell and Donchin in (Farwell

and Donchin, 1988): a matrix of 6×6 symbols. Each

experiment was composed of a training and several

testing stages. During both stages, columns and rows

of the matrix were intensiﬁed (see Figure 1) in a ran-

dom manner. The intensiﬁcation duration was set to

100 ms, followed by a 100 ms of no intensiﬁcation.

Each column and each row ﬂashed only once during

one trial, so each trial consisted of 12 stimulus pre-

sentations.

During the training stage, 11 symbols, taken from

the typing matrix, were presented to the subject. For

each symbol, 10 intensiﬁcation for each row/column

were performed. The subject was asked to count the

Interuniversity Microelectronics Centre (IMEC),

http://www.imec.be

COMPARISON OF LINEAR CLASSIFICATION METHODS FOR P300 BRAIN-COMPUTER INTERFACE ON

DISABLED SUBJECTS

329

Table 1: Information about the patients.

Patient ID Age Gender Diagnosis

subject 1 43 M Amyotrophic lateral sclerosis (2002). Moderate bulbar palsy. Severe weakness

of upper and lower limbs and spasticity in lower limbs.

subject 2 51 M Right MCA stroke (2008) with hypertension (stage II) and mild left hemipare-

sis.

subject 3 58 M Spontaneous SAH and secondary intracerebral hemorrhage in the right hemi-

sphere (2002) with hypertension (stage III) and severe left hemiparesis.

subject 4 54 F Left MCA stroke (2005) with mild motor aphasia and right hemiparesis.

subject 5 52 M Posterior circulation stroke (2002). Right hemiparesis with dysarthria.

subject 6 54 M Left MCA stroke (16.10.2009) with right hemiparesis and motor aphasia.

subject 7 36 M Acute left MCA stroke with partial motor aphasia, right hemisensory loss.

subject 8 65 M Right MCA stroke (2008) with hypertension (stage III) and mild left hemipare-

sis.

number of intensiﬁcations of the corresponded sym-

bol. The counting was used only for keeping subject’s

attention on the symbol.

The recorded data was ﬁltered (in the 0.5–15 Hz

frequency band with a fourth-order zero-phase dig-

ital Butterworth ﬁlter) and properly cut into signal

tracks. Each of these tracks consisted of 1000 ms

of recording, starting from the stimulus onset. Then,

each of these tracks was downsampled, by retaining

every 25th sample, and assigned to one of two pos-

sible groups: target and nontarget, according to the

stimuli that they were locked to. For classiﬁer train-

ing, we constructed a set of 1000 target-, and the same

amount of non-targetaveraged brain responses, where

the averages were taken based on k randomly selected

responses from the corresponding groups. The num-

ber k was equal to the number of intensiﬁcation se-

quences (trails), for each stimulus, during the testing

stage.

Amplitude values at speciﬁc moments in time, of

the downsampled EEG signal, restricted to the in-

terval 100–750 ms after stimuli onset, were taken

as features. All these features were normalized to

their Z-score through the estimation of f

n,t

= (x

(t)−

(t))/σ

(t)

, where x

(t) is the EEG amplitude of n-

th channel (electrode) at time t, after the stimulus on-

set, x

(t) the average of x

(t) and σ

(t)

the standard

deviation for all training examples of both the target

and nontarget recordings of the training set. Com-

bining all those features, we obtained a feature vector

f = [ f

,..., f

]

, which was used as input for the lin-

ear classiﬁer w

+ w

+ ···+ w

+ b = w

f+ b

(see further)

. After substitution of the feature vec-

tor f into the abovementioned equation, we obtain a

Since we use Z-scores as features, and since we use

a balanced training set (equal numbers of target and non-

target responses), the parameter b should be close to zero.

distance (multiplied by factor

√

w) from the point

in feature space to the separating hyperplane, with the

sign indicating to which side of the hyperplane the

point belongs, i.e., the target or non-target class.

After training the classiﬁer, each subject per-

formed several on-line test sessions during which

(s)he was asked to mind-type a few words. The typing

performance (ratio of correctly typed symbols) was

used for estimating the classiﬁcation accuracy. For

these on-line test sessions, we used the classiﬁer that

was trained on data averaged over 15 trials. Thus,

each subject attempted to type a symbol based on 15

row/column intensiﬁcations. During typing, the EEG

data was stored for further off-line analysis based on

a smaller amount k of trials (in this case we used all

k-combination of 15 trails for each typed letter for as-

sessing the accuracy).

The testing stage differs from the training stage

by the way the signal tracks were grouped. During

training, the system “knows” exactly which one of 36

possible symbols is attended by the subject at any mo-

ment of time. Based on this information, the collected

signal tracks can be grouped into only two categories:

target (attended) and non-target (not attended). How-

ever, during testing, the system does not know which

symbol is attended by the subject, and the only mean-

ingful way of grouping is by stimulus type (which in

the proposed paradigm can be one of 12 types: 6 rows

and 6 columns). Thus, during the testing stage, for

each trial, we had 12 tracks (from all 12 groups) of

1000 ms EEG data recorded from each electrode. The

averaged EEG response for each electrode was deter-

mined for each group. The selected features of the av-

eraged data were then fed into the classiﬁer. As a re-

sult, the classiﬁer produces 12 (for each row/column)

values (c

,...,c

) which describe the distance to a

separating hyperplane in the feature space together

with the sign. The row index i

and the column in-

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

330

dex i

of the classiﬁed symbol were calculated as:

= argmax

i=1,...,6

}, and i

= argmax

i=7,...,12

}−6.

The symbol on the intersection of the i

-th row and

-th column in the matrix was then taken as the result

of the classiﬁcation and presented, as a feedback, to

the subject in the on-line session.

3 CLASSIFICATION METHODS

3.1 Fisher’s Linear Discriminant

Analysis

Fisher’s Linear Discriminant Analysis (LDA) is one

of the most widely used classiﬁers in P300 BCI sys-

tems (Krusienski et al., 2006; Panicker et al., 2010).

It was reported that it can even outperform other clas-

siﬁers (Mirghasemi et al., 2006). Its main idea is

to ﬁnd a projection from the N-dimensional feature

space onto a one dimensional space w

f for which

the ratio of the variance between the two classes (tar-

get and non-target) vs. the variance within the classes

is maximal. This ’optimal’ projection is estimated as

w = (Σ

−1

+ Σ

)

−1

(µ

−µ

−1

), where Σ and µ de-

ﬁne the covariances and the means of the two classes

(target and non-target) that need to be separated.

3.2 Stepwise Linear Discriminant

Analysis

Stepwise Linear Discriminant Analysis (SLDA) was

used in the patient studies of P300 BCI (Nijboer

et al., 2008; Sellers and Donchin, 2006). It can be

considered as an extension of LDA with an incor-

porated ﬁlter feature selection. SLDA adds and re-

moves terms from a linear discriminant model based

on their statistical signiﬁcance in regression, thus,

producing modelthat is adjustable to the training data.

It was shown that SLDA performs equally well or

even better than several other classiﬁcation methods

in P300 BCI (Krusienski et al., 2006). For our com-

parison analysis, we have used the same procedure

as in (Krusienski et al., 2006) (in the forward step,

the entrance tolerance p-value < 0.1; in the backward

step, the exit tolerance p-value > 0.15). The process

is iterated until convergence, or until it reaches a pre-

deﬁned number of 60 features.

3.3 Bayesian Linear Discriminant

Analysis

Bayesian Linear Discriminant Analysis (BLDA) was

used for P300 BCI in patients (Hoffmann et al., 2008).

It is based on a probabilistic regression network. As-

sume that the targets t

(in the case of a classiﬁcation

problem these are +1 and −1) are linearly dependent

on the observed features f

= [ f

,..., f

]

with an ad-

ditive Gaussian noise term ε

: t

= w

+ ε

. As-

suming further an independent generation of the ex-

amples from a data set, the likelihood of all data is

p(t|w,σ

) =

∏

i=1

(2πσ

)

−1/2

exp



−

−w

)

2σ



. Ad-

ditionally to this, we have to introduce a prior dis-

tribution over all weights as a zero-mean Gaus-

sian p(w|α) =

∏

j=1



2π



1/2

exp



−



. Using

Bayes’s rule, we can deﬁne the posterior distribu-

tion p(w|t,α,σ

) = (p(t|w, σ

)p(w|α))/p(t|α,σ

which is Gaussian with mean µ = (F

F+σ

αI)

−1

and covariance matrix Σ = σ

F+ σ

αI)

−1

, where

I is an identity matrix and F is a matrix with each

row corresponding to a training example in feature

space, t a column-vector of true labels (classiﬁcation)

for all corresponding training examples. As a result,

our separation plane will have the form µ

f. This so-

lution is equivalent to a penalized least-square esti-

mate E(w) =

2σ

∑

i=1

−w

)

∑

j=1

(Tip-

ping, 2004).

3.4 Linear Support Vector Machine

In P300 BCI research, Support Vector Machine

(SVM) is regarded as one of the more accurate classi-

ﬁers (Thulasidas et al., 2006; Krusienski et al., 2006).

The principal idea of a linear SVM is to ﬁnd the

separating hyperplane, between two classes, so that

the distance between the hyperplane and the clos-

est points from both classes is maximal. In other

words, we need to maximize the margin between

the two classes (Vapnik, 1995). Since it is not al-

ways the case that the two classes are linearly sep-

arable, the linear SVM idea was also generalized to

the case where data points are only required to fall

within the margin (and even are on the wrong side

of the decision boundary) by adding a regularization

term. For our analysis, we used use method proposed

in (Combaz et al., 2010), which uses linear least-

squares SVM (Suykens et al., 2002) to solve the min-

imization problem min

w,b,e

(

w) + γ

∑

i=1

with

respect to y

+ b) = 1 −e

, i = 1,...,n, where f

corresponds to training points in feature space, and y

is the associated output (+1 for the responses to the

target stimulus and −1 for the non-target stimulus).

COMPARISON OF LINEAR CLASSIFICATION METHODS FOR P300 BRAIN-COMPUTER INTERFACE ON

DISABLED SUBJECTS

331

Figure 2: Classiﬁcation accuracy as a function of the number of intensiﬁcations for every subject, and for all discussed

classiﬁcation methods.

The regularization parameter is estimated through a

line search on cross-validation results.

3.5 Method based on Feature

Extraction

Another classiﬁcation method in P300 BCI research

(Chumerin et al., 2009) relies on the one-dimensional

version of a linear feature extraction (FE) ap-

proach proposed by Leiva-Murillo and Art´es-Rodr´ı-

guez in (Leiva-Murillo and Artes-Rodriguez, 2007).

The method searches for the ”optimal” subspace max-

imizing (an estimate of) the mutual information be-

tween the set of projections Y = {w

} and the set

T of corresponding labels t

= {−1,+1}. Accord-

ing to (Leiva-Murilloand Artes-Rodriguez, 2007), the

mutual information between the set of projections Y,

and the set of corresponding labelsC can be estimated

as: I(Y,C) =

∑

p=1

p(t

)(J(Y|t

) −logσ(Y|t

)) −

J(Y), with N

= 2 the number of classes, Y|t

the

projection of the p-th class’ data points onto the di-

rection w, σ(·) the standard deviation, and J(·) the

negentropy, estimated using Hyv¨arinen’s robust esti-

mator (Hyv¨arinen, 1998).

4 RESULTS

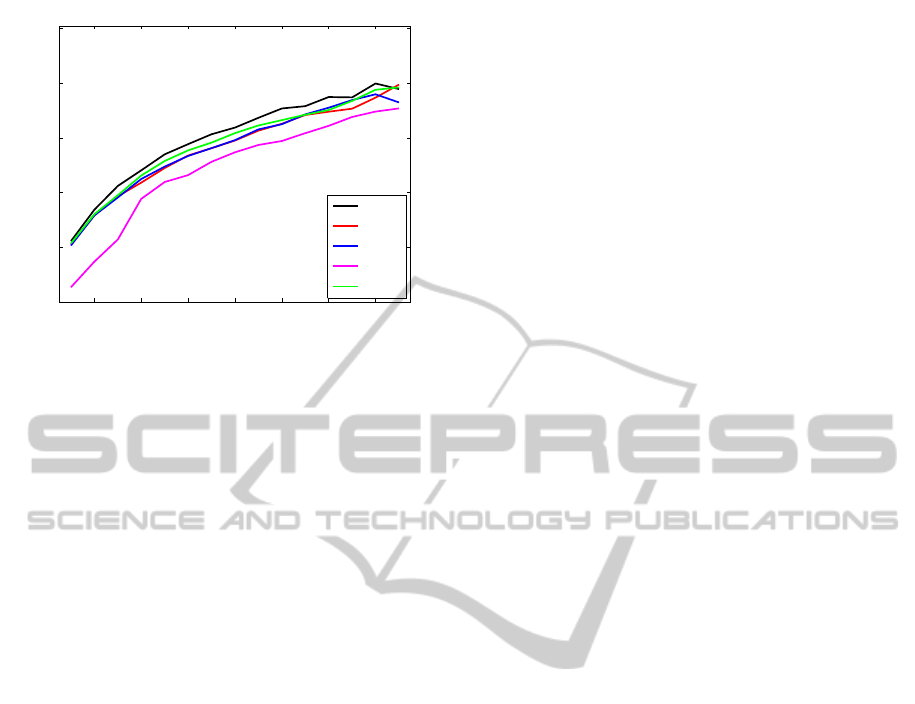
The performance results are shown in Figure 2 for in-

dividual subjects, and in Figure 3 as a grand average

among all subjects. In order to verify the statistical

signiﬁcance of the comparison, we used the nonpara-

metric Friedman’s test (Corder and Foreman, 2009)

between each pairs of different methods to test the

difference in the medians of the accuracy results. We

have found that the accuracy based on BLDA is sig-

niﬁcantly (p < 0.001) better than any other. Linear

SVM is second. As for SLDA and LDA, there is no

any signiﬁcant difference between them.

We have also analyzed the mistyped (erroneously

detected) symbols [results not shown]. We havefound

that, for all classiﬁcation method, the misclassiﬁca-

tions mostly occur for either a misclassiﬁed row or

column, and the erroneously typed symbols are in

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

332

2 4 6 8 10 12 14

100

Intensification sequences

Accuracy (%)

BLDA

LDA

SLDA

SVM

Figure 3: Average classiﬁcation accuracy as a function of

the number of intensiﬁcations for all discussed classiﬁca-

tion methods.

close proximity on the screen to the desired ones.

We observed that some subjects were not com-

fortable with the visual stimulation protocol we used

during the on-line sessions. This discomfort was ex-

pressed by the frequent (3–8 Hz) eye blinking of the

subjects. For those subjects, we had to adapt the stim-

ulation protocol in terms of the interstimuli interval,

which was increased up to 300 ms (150 ms of inten-

siﬁcation followed by 150 ms of no intensiﬁcation).

This shows that working with patients can be quite

different.

5 CONCLUSIONS

We have compared ﬁve linear classiﬁcation methods

for a P300-based BCI, tested on disabled patients. We

have found that BLDA yields signiﬁcantly better re-

sults compared to the other classiﬁcation methods we

considered, with linear SVM as the second one in

accuracy. These results can be helpful in deciding

what classiﬁer to use for patients. Additionally to this,

since the classiﬁers could produce differentoutcomes,

one could beneﬁt from combining them using a co-

training approach (Panicker et al., 2010), to improve

the classiﬁcation performance.

ACKNOWLEDGEMENTS

NVM is supported by the Flemish Regional Min-

istry of Education (Belgium) (GOA 10/019). NC is

supported by the European Commission (IST-2007-

217077). AC is supported by a specialization grant

from the Agentschap voor Innovatie door Weten-

schap en Technologie (IWT, Flemish Agency for In-

novation through Science and Technology). MMVH

is supported by research grants received from the

Excellence Financing program (EF 2005) and the

CREA Financing program (CREA/07/027) of the

K.U.Leuven, the Belgian Fund for Scientiﬁc Research

- Flanders (G.0588.09), the Interuniversity Attraction

Poles Programme – Belgian Science Policy (IUAP

P6/054), the Flemish Regional Ministry of Education

(Belgium) (GOA 10/019), and the European Commis-

sion (STREP-2002-016276, IST- 2004-027017, and

IST-2007-217077), and by the SWIFT prize of the

King Baudouin Foundation of Belgium.

The authors wish to thank Valiantsin Raduta and

Yauheni Raduta from Neurology Department of Brest

Regional Hospital (Brest, Belarus) for the assistance

with the recording of EEG data on patients. The

authors also grateful to Refet Firat Yazicioglu, Tom

Torfs and Cris Van Hoof from the Interuniversity Mi-

croelectronics Centre (IMEC) in Leuven for provid-

ing with the wireless EEG system.

We would like to thank Prof. Philip Van Damme

from Experimental Neurology Department at Katho-

lieke Universiteit Leuven for his help in translating

the diagnoses from Russian.

REFERENCES

Chumerin, N., Manyakov, N. V., Combaz, A., Suykens,

J. A., Yazicioglu, R. F., Torfs, T., Merken, P., Neves,

H. P., Van Hoof, C., and Van Hulle, M. M. (2009).

P300 detection based on feature extraction in on-line

brain-computer interface. Lecture Notes in Computer

Science, 5803:339–346.

Combaz, A., Chumerin, N., Manyakov, N. V., Suykens, J.,

and Van Hulle, M. M. (2010). Error-related potential

recorded by eeg in the context of a p300 mind speller

brain-computer interface. In Machine Learning for

Signal Processing, IEEE Workshop on, pages 65–70,

Kittil¨a, Finland.

Corder, G. and Foreman, D. (2009). Nonparametric Statis-

tics for Non-Statisticians: A Step-by-Step Approach.

New York, J. Wiley.

Farwell, L. and Donchin, E. (1988). Talking off the top of

your head: toward a mental prosthesis utilizing event-

related brain potentials. Electroencephalography and

clinical Neurophysiology, 70(6):510–523.

Hoffmann, U., Vesin, J.-M., E. T., and Diserens, K. (2008).

An efﬁcient P300-based brain-computer interface for

disabled subjects. Journal of Neuroscience Methods,

167:115–125.

Hyv¨arinen, A. (1998). New approximations of differen-

tial entropy for independent component analysis and

projection pursuit. In Proceedings of the 1997 con-

ference on Advances in neural information processing

COMPARISON OF LINEAR CLASSIFICATION METHODS FOR P300 BRAIN-COMPUTER INTERFACE ON

DISABLED SUBJECTS

333

systems, pages 273–279. MIT Press Cambridge, MA,

USA.

Krusienski, D., Sellers, E., Cabestaing, F., Bayoudh, S.,

McFarland, D., Vaughan, T., and Wolpaw, J.(2006). A

comparison of classiﬁcation techniques for the P300

Speller. J. Neural. Eng., 3:299–305.

Leiva-Murillo, J. and Artes-Rodriguez, A. (2007). Maxi-

mization of mutual information for supervised linear

feature extraction. IEEE Transactions on Neural Net-

works, 18(5):1433–1441.

Lotte, F., Congedo, M., L´ecuyer, A., Lamarche, F., and Ar-

naldi, B. (2007). A review of classiﬁcation algorithms

for EEG-based Brain-Computer Interface. Journal of

Neural Engineering, 4:R1–R13.

Luck, S. (2005). An introduction to the event-related poten-

tial technique. MIT Press Cambridge, MA.

Mirghasemi, H., Fazel-Rezai, R., and Shamsollahi, M.

(2006). Analysis of P300 classiﬁers in Brain Com-

puter Interface speller. In Proceedings of the 28th

IEEE EMBS Annual International Conference, pages

6205–6208.

Nijboer, F., Sellers, E., Mellinger, J., Jordan, M., Matuz,

T., Furdea, A., Halder, S., Mochty, U., Krusienski, D.,

Vaughan, T., Wolpaw, J., Birbaumer, N., and K¨ubler,

A. (2008). A P300-based brain-computer interface

for people with amyotrophic lateral sclerosis. Clini-

cal Neurophysiology, 119:1909–1916.

Panicker, R., Puthusserypady, S., and Sun, Y. (2010). Adap-

tation in P300 Brain-Computer Interface: A two-

classiﬁer co-training approach. IEEE Trans Biomed

Eng, 57.

Piccione, F., Giorgi, F., Tonin, P., Priftis, K., Giove, S., Sil-

voni, S., Palmas, G., and Beverina, F. (2006). P300-

based brain-computer interface: Reliability and per-

formance in healthy and paralysed participants. Clin-

ical Neurophysiology, 117:531–537.

Sajda, P., M¨uller, K.-R., and Shenoy, K. (2008). Brain-

computer interfaces. IEEE Signal Proccessing Maga-

zine, 25(1):16–17.

Sellers, E. and Donchin, E. (2006). A P300-based brain-

computer interface: Initial test by ALS patients. Clin-

ical Neurophysiology, 117:538–548.

Sellers, E., Vaughan, T., and Wolpaw, J. (2010). A brain-

computer interface for long-term independent home

use. Amyotrophic Lateral Sclerosis, pages 1–7.

Silvoni, S., Volpato, C., Cavinato, M., Marchetti, M.,

Priftis, K., Merico, A., Tonin, P., Koutsikos, K., Bev-

erina, F., and Piccione, F. (2009). P300-Based Brain-

Computer Interface Communication: Evaluation and

Follow-up in Amyotrophic Lateral Sclerosis. Fron-

tiers in Neuroscience, 3(60):1–12.

Suykens, J., Van Gestel, T., De Brabanter, J., De Moor, B.,

and Vanderwalle, J. (2002). Least square support vec-

tor machines. World Scientiﬁc, Singapore.

Thulasidas, M., Guan, C., and Wu, J. (2006). Robust clas-

siﬁcation of EEG signal for brain-computer interface.

IEEE Transactions on Neural Systems and Rehabili-

tation Engineering, 14(1):24–29.

Tipping, M. E. (2004). Bayesian inference: An introduc-

tion to principles and practice in machine learning. In

Bousquet, O., von Luxburg, U., and R¨atsch, G., edi-

tors, Advanced Lectures on Machine Learning, pages

41–62. Springer.

Vapnik, V. (1995). The Nature of Statistical Learning The-

ory. Springer-Verlag.

Yazicioglu, R., Merken, P., Puers, R., and Van Hoof, C.

(2006). Low-power low-noise 8-channel EEG front-

end ASIC for ambulatory acquisition systems. In The

32nd European Solid-State Circuits Conference. Pro-

ceedings of, pages 247–250.

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

334