TOOL PATH PLANNING IN FLANK MILLING BASED ON DUAL

SPHERICAL SPLINE

Yayun Zhou

Siemens AG, CT T DE TC3/GTF MSO, Otto-Hahn-Ring 6, 81739 Munich, Germany

org Schulze

Universit

at Stuttgart, Pfaffenwaldring 47, 70569 Stuttgart, Germany

Stefan Sch

afﬂer

Universit

at der Bundeswehr M

unchen, Werner-Heisenberg-Weg 39, 85577 Neubiberg, Germany

Keywords:

Ruled surface, Blade design, Flank milling, Dual spherical spline.

Abstract:

The ﬂank milling (side milling) method, which uses the manufacturing tool side to remove material, is widely

used in industry to manufacture ruled surfaces. Ruled surfaces are often used in blade design considering the

aerodynamics requirements and the manufacture cost. A common way to derive a ﬂank millable blade surface

is to adopt a certain ruled surface approximation algorithm before the surface is delivered to the manufacturer.

In this paper, a new tool path planning approach is proposed based on the offset theory and the kinematic ruled

surface approximation. The novelty of this approach is to denote the drive surface as a dual spherical spline,

which is a new ruled surface representation. This drive surface is derived by kinematically approximating the

offset surface of the original design as a ruled surface. Therefore, the designed blade surface is represented as

a ﬂank milling tool path with a cylindrical cutter in CNC machining. This approach delivers more accuracy

compared with convectional tool position optimization methods. By integrating the manufacture requirements

into the design phase, this approach also reduces the developing cycle time and the manufacturing cost.

1 INTRODUCTION

Considering the aerodynamics requirements and the

manufacturing cost, blade surfaces are usually de-

signed as ruled surfaces, which are a special type of

surfaces that can be generated by moving a line in

space. In industry, the ﬂank milling method is of-

ten used to machine ruled surfaces. Different from

the face milling (point milling) method, ﬂank milling

(side milling) uses the side of the manufacturing tool

instead of the tip of the manufacturing tool to touch

the surface and remove the stock in front of the cut-

ter. Since the whole length of the cutter is involved

in the cutting process, this method has high mate-

rial removal rate and high machining efﬁciency. Be-

sides, no scallops are left behind in single pass ﬂank

milling, less surface ﬁnishing work is required. Espe-

cially for the manufacturing of a turbocharger com-

pressor/impeller, it is necessary to use 5-axis ﬂank

milling, because the tunnel between two adjacent

blades is too small with respect to the size of blades.

Hence, designing a ﬂank millable blade is appealing

in many ﬁelds.

A common way to derive a ﬂank millable blade

surface is to adopt a certain ruled surface approxi-

mation algorithm before the surface is delivered to

the manufacturer. Theoretically, if the manufactur-

ing tool is considered as a line, a ruled surface can be

accurately produced by moving this line. However,

the machine tool usually has certain size and shape

(i.e., cylindrical cutter or conical cutter), so the ideal

position for the cutting tool is to offset the ruling in

the direction of a surface normal at a distance equal

to the radius of the cutting tool. Because the surface

normals rotate along the ruling, at some point the cut-

ting tool will begin to deviate from the desired sur-

face. Generally, the machined surface is not a ruled

surface, but a curved surface. At each tool position,

the effective contact between the cutting tool and the

swept surface is a curve (grazing curve), not a straight

line.

Researchers developed a variety of cutter location

Zhou Y., Schulze J. and Schäfﬂer S..

TOOL PATH PLANNING IN FLANK MILLING BASED ON DUAL SPHERICAL SPLINE.

DOI: 10.5220/0003274600050012

In Proceedings of the International Conference on Computer Graphics Theory and Applications (GRAPP-2011), pages 5-12

ISBN: 978-989-8425-45-4

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

(CL) data optimization methods to minimize the man-

ufacturing error. The simplest way is to locate a cylin-

drical cutting tool tangentially to the given surface at

one point on the ruling and make the tool axis parallel

to the ruling. Alternatively, the tool can also be posi-

tioned to touch two points on the ruling. Both ideas

belong to the direct tool position method (Liu, 1995).

An improvement of the direct tool position method

is to locate the tool step by step (Choi et al., 1993)

(Menzel et al., 2004). In those approaches, the initial

position of the cutting tool is determined by one of

the direct tool position methods, afterwards the tool

is lifted and twisted in order to reduce the manufac-

turing error. The computation time of the step by step

method is usually long. The third type of tool posi-

tioning method combines the techniques used in the

two classes above. The tool contacts three points on

the given surface (two on the guiding curves and one

on the ruling). Those three points are obtained by

solving seven transcendental equations based on cer-

tain geometrical conditions (Redonnet et al., 1998).

However, those methods all focus on the local er-

ror reduction corresponding to each tool location. The

kinematic error between successive CL points can

still be large. In order to get a global optimal tool path,

a new type of approach is developed (Gong et al.,

2005) (Chu and Chen, 2006) (Senatore et al., 2008)

(Zhou et al., 2009). The authors propose a global op-

timization method to generate the tool axis trajectory

surface which is also a ruled surface. The cutting tool

is positioned so that the maximum deviation between

the tool axis trajectory surface and the offset surface

is minimized. The trajectory surface of the tool axis

(drive surface) is often represented as a tensor prod-

uct B-spline surface, therefore each tool position is

determined.

In this paper, we propose a new strategy to repre-

sent the drive surface as a dual spherical spline (Zhou

et al., 2010), in which every ruling of the ruled surface

is written as a dual vector. It indicates the orientation

of the tool axis with respect to a speciﬁc point on the

workpiece and has the same mathematical represen-

tation of screws (Dimentberg, 1965). Using the dual

vector calculation rules, the tool axis position is eas-

ily converted to the tool motion. Compared with the

conventional tensor product B-spline surface repre-

sentation, it is more effective to specify a 5-axis CNC

machining tool path by relating both the position and

orientation to a single parameter. Based on this repre-

sentation, it is possible to check whether the desired

path is within the workspace of the machine tool by

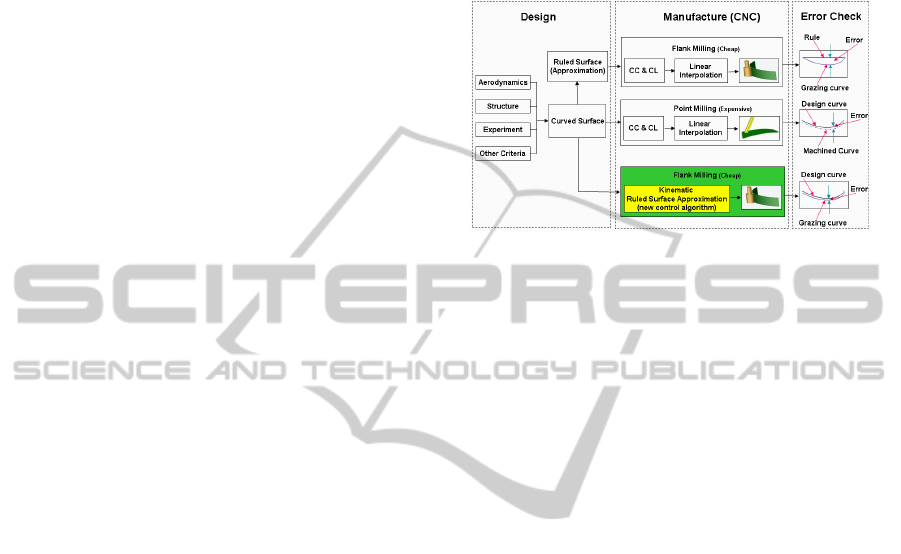
applying the kinematics and robotics analysis. Fig. 1

compares this new approach with the conventional de-

sign and manufacturing methods. The new approach

not only inherits the advantages of global path opti-

mization methods which ensure low manufacturing

cost and avoid introducing double errors, but also pro-

vides a novel representation which is closely linked to

the tool movement.

Figure 1: A comparison of different design and manufac-

turing diagram.

The organization of this paper is as follows. Sec-

tion 2 lays the theoretical basis of this approach, in-

cluding the offset theory and ruled surface represen-

tations. Then the deﬁnition of dual spherical spline is

brieﬂy introduced and its advantages in motion con-

version are shown in Section 3. In Section 4, the drive

surface is derived from the offset surface of original

design based on a kinematic ruled surface approxi-

mation algorithm. This algorithm can be modiﬁed to

embrace more manufacture constrains corresponding

to difference CNC machines. This approach is tested

with some given turbocharger blade surfaces. The

simulation results are presented in Section 5. Finally,

a conclusion is drawn in Section 6.

2 THEORETICAL BASIS

The approach proposed in this paper mainly contains

two key steps: ﬁrst deriving an offset surface from the

original design, then generating a drive surface from

the offset data. The drive surface is a ruled surface,

which is denoted as a dual spherical spline. In this

section, the offset theory and representations of ruled

surface are introduced.

2.1 Offset Theory

If R(u) = R(u

, u

) represents a surface, its offset

surface R

(u) is deﬁned by the equation (Marciniak,

1991):

(u) = R(u) + d ·n(u), (1)

where n is a normal vector in R(u) and d is the dis-

tance between the surfaces. This is the classical offset

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

surface deﬁnition. It is also referred to as parallel off-

set. In (Pottmann et al., 1996), Pottmann and L

u study

the “circular offset” of ruled surfaces, which arises

when a cylindrical or conical cutter with a circular

edge is used in ﬂank milling. The authors proved that

the circular offsets of a rational ruled surface are ra-

tional in general except the developable surfaces and

conoidal ruled surfaces with generators orthogonal to

the tool-axis. The offset of a ruled surface is in gen-

eral not a ruled surface. In fact, the offset curve of a

nontorsal generator with respect to a ruled surface is

a rational quadric (Pottmann et al., 1996).

For ruled surfaces, we often meet the concept

Bertrand offset. It is a generalization of the theory

of Bertrand curves based on line geometry. A pair of

curves are Bertrand mates if there exists a one-to-one

correspondence between their points such that both

curves share a common principal normal at their cor-

responding points (Ravani and Ku, 1991). Consid-

ering the ruled surface in the context of line geome-

try, the ruled surface is represented as a one-parameter

family of lines. Simply speaking, we have the follow-

ing deﬁnition (Ravani and Ku, 1991):

Deﬁnition 2.1. Two ruled surfaces are said to be

Bertrand offsets of one another if there exists a one-to-

one correspondence between their rulings such that

both surfaces have a common principal normal at the

striction points of their corresponding rulings.

For the Bertrand offsets, we have an important

theorem (Ravani and Ku, 1991):

Theorem 2.1. Two ruled surfaces which are Bertrand

offsets of each other as deﬁned in Deﬁnition 2.1 are

constant offsets of one another.

Inspired by this theorem, if the given surface is

a ruled surface, the drive surface can be derived by

constructing the Bertrand offset of the given surface.

Consequently, the given surface is also a Bertrand off-

set surface of the drive surface. This relationship pro-

vides the initial inspiration of our approach. Gener-

ally, the original designed surface is not a ruled sur-

face. In our algorithm, we calculate the “circular off-

set” of the given surface instead.

2.2 Ruled Surface Representations

In Euclidean space R

, a ruled surface Φ possesses a

parametric representation (Edge, 1931):

x(u, v) = a(u) + vr(u), u ∈ I, v ∈ R, (2)

where a(u) is called the directrix curve and r(u)

is a direction vector of generator. Alternatively, a

ruled surface Φ can be parameterized by two direc-

trix curves p(u) and q(u):

x(u, v) = (1 −v)p(u) + vq(u). (3)

The straight line denoted as x(u

, v) = (1 −v)p(u

vq(u

) is called a ruling.

By applying the Klein mapping and the Study

mapping, a ruled surface can be written in a more

compact way using dual numbers. The dual numbers

were ﬁrst introduced by Clifford (Clifford, 1873). A

dual number can be written in the form ˆa = a + εa

◦

where a, a

◦

∈ R and ε is the dual element with:

ε 6= 0,

0ε = ε0 = 0,

1ε = ε1 = ε,

= 0.

(4)

Extending the dual numbers to the vector space,

the space D

is deﬁned as a set of all pairs of vectors:

a = a + εa

◦

where a, a

◦

∈ R

. (5)

In line geometry, a line in Euclidean space can

be represented as a unit vector in D

(Pottmann and

Wallner, 2001). Those unit vectors constitute a sphere

called Dual Unit Sphere (DUS). In this form, a ruled

surface deﬁned by Eq. (2) is written as a curve on the

DUS :

L(u) = l(u) + εl

◦

(u) =

r(u)

kr(u)k

+ ε

a(u) ×r(u)

kr(u)k

. (6)

A dual vector representation of ruled surface can

be converted to a point representation:

x(u, v) = l(u) ×l(u)

◦

+ vl(u). (7)

Now, a mapping between a ruled surface represen-

tation in Euclidean space and a curve representation

on the DUS is set up. Instead of solving a surface ap-

proximation problem in the Euclidean space, we solve

a curve approximation problem on the DUS.

3 DEFINITION OF DUAL

SPHERICAL SPLINE

The dual vector representation of ruled surface

links the path and the physical motion of the tool

(Sprott and Ravani, 1997) (Sprott and Ravani, 2001).

K. Sprott proposed an algorithm to generate a free-

form curve on the DUS (Sprott, 2000), but deﬁning

a spline strictly lying on the DUS is not trivial. Due

to the non-linearity of the space, conventional spline

deﬁnitions as a linear combination of basis functions

are not working on the DUS.

3.1 Dual Spherical Spline

The deﬁnition of dual spherical spline is inspired by

(Buss and Fillmore, 2001), in which a spline on a real

TOOL PATH PLANNING IN FLANK MILLING BASED ON DUAL SPHERICAL SPLINE

sphere is deﬁned based on a least squares minimiza-

tion. Based on the transfer principle, which simply

states that for any operation deﬁned for a real vector

space, there is a dual version with similar interpreta-

tion, we can derive a similar deﬁnition of a spline on

the DUS:

Deﬁnition 3.1. Let

, . . . ,

be control points on the

Dual Unit Sphere

in D

: a spline on the DUS is

deﬁned as a result of a least squares minimization. In

other words, it contains the points

s(t) on

which

minimizes the value:

f (

s(t)) =

∑

·dist

(

s(t),

)

, (8)

where dist

(

s(t),

) is the dual spherical distance be-

tween

s(t) and

. This spline on the DUS is denoted

as a dual spherical spline:

s(t) =

∑

i=1

(t)

. (9)

The distance between two points on the DUS is

deﬁned by a dual angle between two lines. It has the

form

θ = θ + εd, where θ is the angle between the

lines and d is the minimum distance along the com-

mon perpendicular. For two points

x and

y on the

DUS, we have the following equation:

x ·

y = cos

θ. (10)

The dual arc cosine function is deﬁned as:

θ = cos

−1

(x + εx

◦

) = cos

−1

(x) −ε

◦

√

1 −x

. (11)

The basis functions of a dual spherical spline must

always satisfy the property:

∑

i=1

(t) = 1, f

(t) ≥ 0 ∀i, (12)

for t in the interval [a, b].

Since Bernstein polynomials and B-spline basis

functions both satisfy the requirement Eq. (12), the

dual spherical B

ezier curve or B-spline curve

s(t) can

be deﬁned in the form of Eq. (9).

It is proven that there is a neighborhood of

, . . . ,

, in which the

s(t) is a C

∞

-function of

, . . . ,

. Hence the regularity of the dual spheri-

cal spline is determined by the basis functions. The

proof of uniqueness and continuity property follows

the similar strategy as (Buss and Fillmore, 2001), the

details can be found in (Zhou, 2010).

3.2 Advantages in Motion Conversion

Now the drive surface, which is a ruled surface, is rep-

resented as a continuous, differentiable dual spherical

spline

x(u). Following this deﬁnition, a local coordi-

nate frame can be set up consisting of three concurrent

lines – {

t}. This frame is called generator trihe-

dron, where

x represents a ruling and the other two

lines are deﬁned by the following equations:

t =

x(u)

n =

x ×

(13)

The line

t is called the central tangent, which is tan-

gent to the surface at the striction point. The line

called central normal is the normal of the surface at

the striction point. It can be proven that these three

lines are orthogonal to each other and the intersection

point of the three lines is the striction point of the rul-

ing

x. This point is the point of minimum distance

between neighboring rulings. The locus of striction

points is called the striction curve (Sprott and Ravani,

2007). The generator trihedron can be rewritten as

dual vectors:

x = x + ε(a ×x),

n = n + ε(a ×n),

t = t + ε(a ×t),

(14)

where a is the striction point, x is a vector directing

along the ruling, the vector t is perpendicular to x and

tangent to the surface at the striction curve, the vector

n is perpendicular to x and t. Fig. 2 shows this frame

on a ruled surface. The center line of the cylindrical

cutter (a ruling of the drive surface) undergoes a screw

motion about the axis

t. According to the screw the-

ory, the distance between successive rulings is deﬁned

as a dual angle between two screws. The successive

rulings are denoted as

x(u

) =

∑

i=0

i, p

)

and

x(u

) =

∑

i=0

i, p

)

. The dual angle is

calculated by the following equations:

= cos

ω = x + εx

◦

, (15a)

ω = φ + εd

= cos

−1

( ˆx)

= cos

−1

(x + εx

◦

)

= cos

−1

(x) −ε

◦

√

1−x

(15b)

This means the cutter tool translates the distance

d and rotates the angle φ along the axis

t in order to

move from position

to position

. The ratio be-

tween d and φ is called distribution parameter (Sprott,

2000):

p =

. (16)

The distribution parameter indicates the amount of

twisting associated with the ruled surface. A cone

or tangent developable surface has a zero valued dis-

tribution parameter, while the distribution parameter

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

Figure 2: Generator trihedron on ruled surface.

of parallel rulings remains undeﬁned. Generally, a

twisted ruled surface has a non-zero distribution pa-

rameter. If adopting time t as the parameter of the

dual spherical spline, it is quite easy to convert the

tool path to the motion code. The velocity of the line

is given by the expression:

x =

ω ×

x, (17)

where the angular velocity vector

ω = ω + εv denotes

the rotation and translation along the screw axis

t. In

this local coordinate frame, an arbitrary point P along

the ruling is written as P = sr, where r =

kxk

and s

is the distance from the striction point a. The velocity

of this point will have a term perpendicular to r due to

the rotation about the line

t and a term in the direction

t due to the translation along the line. The velocity

of the point can be written as (Sprott, 2000):

= ωt ×sr + vt

= −ωsn + vt.

(18)

4 TOOL PATH PLANNING

APPROACH

Based on the deﬁnition of dual spherical spline, a

kinematic approximation algorithm is developed to

construct a ruled surface from an offset surface. This

ruled surface is the drive surface. In this paper,

we propose a tool path planning approach for ﬂank

milling with cylindrical tools. The framework of the

tool path planning approach contains four parts:

1. Generate an offset surface from the original de-

sign surface according to the tool radius

2. Extract the CL data from the offset surface and

write the coordinates as dual vectors

3. Apply the kinematic ruled surface approximation

algorithm

4. Evaluate the dual spherical B-spline with the dual

spherical weighted average algorithm and convert

it to tool motion

In this section, we brieﬂy introduce the key steps of

this approach.

4.1 Offset Surface Generation and CL

Data Extraction

Initially, the blade surface is designed as a free-form

surface. In order to derive the cutter location (CL)

data, the original design is taken as an input and the

offset surface is derived according to Eq. 1. The dis-

tance d between the offset surface and the original de-

sign equals to the radius of the cylindrical tool. The

cutter locations are determined by a ruling search pro-

cess. It is to ﬁnd a discrete system of line segments

close to the given surface. In order to ﬁt the manu-

facture procedure, the search process starts from the

leading edge of the blade surface and marches to-

wards the trailing edge. The lines are chosen using

the least squares minimization method. The march

distance is constrained by the velocity of the milling

machine and most importantly, the intersection of the

line segments must be avoided. Other constrains of

manufacture machines can also inﬂuence the search

process. In the end of this step, a sequence of line

segments l

, . . . , l

are obtained which are close to the

given surface. The details of this step can be found in

(Chen and Pottmann, 1999).

4.2 Kinematic ruled Surface

Approximation

After the rulings are extracted and represented as dual

vectors, a kinematic ruled surface approximation al-

gorithm is applied to approximate the line sequences

as a ruled surface. The manufacture machine con-

strains should be included in the objective functional.

Due to the variety of manufacture systems, the main

task for this paper is to minimize the difference be-

tween the offset surface and drive surface. Its essence

is a dual spherical spline interpolation algorithm on

the DUS. In this paper, we take the dual cubic B-

spline interpolation algorithm as an example. It can

be easily extended to higher order B-splines.

The key idea of this algorithm is to use the loga-

rithmic map which maps all points

on the DUS to

the tangent hyperplane at

q, then interpolate the points

in the hyperplane and maps the result back to the DUS

by the exponential map. As long as the given points

satisfy the uniqueness condition, the algorithm con-

verges. Fig. 3 shows the ﬂowchart of the dual spher-

ical cubic B-spline interpolation algorithm, in which

the logarithmic map l

(·) maps the point

to the tan-

gent hyperplane at

q and the exponential map exp

(·)

maps the result back to the DUS. α

, β

, γ

denote the

TOOL PATH PLANNING IN FLANK MILLING BASED ON DUAL SPHERICAL SPLINE

non-zero elements in the basis matrix:







1 0 0 . . . 0 0

0 . . . 0

0 α

0 . . . 0 α

n−1

0 0 . . . 0 0 1







. (19)

Figure 3: Flowchart of the dual spherical cubic B-spline

interpolation algorithm.

4.3 Dual Spherical Spline Evaluation on

the DUS

After the control points are derived, the dual spherical

B-spline is evaluated as weighted averages of control

points. The weighted average on the DUS is deﬁned

similarly:

Deﬁnition 4.1. Let

, . . . ,

be points on the Dual

Unit Sphere

in D

: a weighted average of these n

points using real weight values ω

, . . . , ω

such that

each ω

≥ 0 and

∑

= 1 is deﬁned as a result of a

least squares minimization. In other words, it is the

point

C on

which minimizes the value:

f (

C) =

∑

·dist

(

)

, (20)

where dist

(

) is the dual spherical distance be-

tween

C and

. The weighted average on the DUS is

denoted as:

C =

∑

i=0

. (21)

The ﬂowchart of the algorithm calculating the

weighted average on the DUS is shown in Fig. 4.

Figure 4: Flowchart of the algorithm calculating the

weighted average on the DUS.

5 SIMULATION RESULT

We test this approach with different blade surfaces

and simulate the manufacturing process of a blade

with a cylindrical cutter. A blade consists of two

sides: pressure surface and suction surface. The tool

path planning strategies for both sides are similar.

Here, we only take one example to explain the pro-

cedure.

To achieve large material removal rate, the radius

of the cylinder should be large, but it must be less

than the distance between two blades. Therefore, for

different blades, the tool sizes are varied. For this test

case, the radius of the cylinder is chosen as R = 2 mm.

The input ﬁle is a “blade.ibl” ﬁle generated by a

software “Bladegen”. It contains discrete points on

blade surfaces. We ﬁrst extract the data for the pres-

sure side of the blade. The offset surface is derived

based on Eq. (1) and d = R.

The simulation results of this approach are shown

in Fig. 5. Fig. 5(a) shows the given surface and its

offset surface. Fig. 5(b) shows the discrete cutter lo-

cations which are extracted from the offset surface.

An afﬁne map is applied to the data due to conﬁdential

requirements.

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

(a) (b)

Figure 5: Design a ﬂank millable turbocharger blade: (a)

Given blade surface (colored) and offset surface (red); (b)

CL data; (c) Movement of the cutter and the produced sur-

face; (d) Comparison between the given surface (colored)

and the produced surface (red).

Then the kinematic ruled surface approximation algo-

rithm is applied to the offset surface to get the drive

surface as a ruled surface. Fig. 5(c) shows the move-

ment of the cylindrical cutter. Consequently, a sur-

face is produced due to the movement of the cylindri-

cal cutter. Fig. 5(d) compares the produced surface

with the original design surface. We evaluate the er-

ror between two surfaces as the distance along z direc-

tion. The average error for these two surface is only

0.0027mm, which is much smaller compared with

the convectional tool position optimization methods.

Since the blade is designed as a tool path, this blade

can be manufactured accurately.

Based on the approach described above, we get a

ﬂowchart of a turbocharger blade design and manu-

facture. In Fig. 6, the design and manufacture phases

are combined together. This new approach avoids in-

troducing the approximation error twice and reduces

the developing time.

Figure 6: A novel design and manufacturing procedure for

turbocharger blades.

6 CONCLUSIONS AND FUTURE

WORK

In this paper, we propose a novel way to plan a tool

path for the blade manufacture with the ﬂank milling

method. It combines the kinematic ruled surface ap-

proximation algorithm with the offset theory. Inte-

grating the constrains of different CNC machines, it

can be used as a control program to guide the move-

ment of the manufacturing tool in ﬂank milling pro-

cess. A tool path of a cylindrical cutter is given in the

form of a dual spherical spline, which describes the

movement of the cylindrical cutter axis. This repre-

sentation of tool path provides a convenient conver-

sion to the tool motion, which leads naturally to the

post-process. Adopting this new approach to design

blade surfaces embraces the manufacturing require-

ments, which ensures low manufacture cost in the de-

sign phase. This approach can also be adapted to gen-

erate tool path for face milling, because the movement

of the tool axis constitutes a ruled surface. For that ap-

plication, the objective is to generate a tool path that

is related to the normals of the surface. Besides, the

manufacturing tool is not only limited to a cylinder.

It can be a cone or other general shapes. Considering

the different geometry of the manufacturing tools, this

algorithm has many other applications. There is still

a lot of work that can be accomplished in this area.

REFERENCES

Buss, S. R. and Fillmore, J. P. (2001). Spherical averages

and applications to spherical splines and interpolation.

ACM Transactions on Graphics, 20(2):95–126.

Chen, H. and Pottmann, H. (1999). Approximation by ruled

surfaces. J. Comput. Appl. Math., 102(1):143–156.

Choi, B. K., Park, J. W., and Jun, C. S. (1993). Cutter-

location data optimization in 5-axis surface machin-

ing. Computer Aided Design, 25(6):377–386.

Chu, C. H. and Chen, J. T. (2006). Tool path planning for

ﬁve-axis ﬂank milling with developable surface ap-

proximation. The International Journal of Advanced

Manufacturing Technology, 29(7-8):707–713.

Clifford, W. K. (1873). Preliminary sketch of biquaternions.

In Tucker, R., editor, Mathematical Papers. Macmil-

lan.

Dimentberg, F. M. (1965). The screw calculus and its appli-

cation in mechanics. Clearinghouse for Federal Scien-

tiﬁc and Technical Information, Springﬁeld, Virginia.

English Translation: AD680993.

Edge, W. (1931). Thoery of ruled surface. Cambridge Univ.

Press.

Gong, H., Cao, L. X., and Liu, J. (2005). Improved po-

sitioning of cylindrical cutter for ﬂank milling ruled

surfaces. Computer Aided Design, 37:1205–1213.

TOOL PATH PLANNING IN FLANK MILLING BASED ON DUAL SPHERICAL SPLINE

Liu, X. (1995). Five-axis NC cylindrical milling of sculp-

tured surfaces. Computer Aided Design, 27(12):887–

894.

Marciniak, K. (1991). Geometric modeling for numerically

controlled machining. Oxford University Press, New

York, USA.

Menzel, C., Bedi, S., and Mann, S. (2004). Triple tangent

ﬂank milling of ruled surface. Computer Aided De-

sign, 36(3):289–296(8).

Pottmann, H., L

u, W., and Ravani, B. (1996). Rational ruled

surface and their offsets. Graphical Models and Image

Processing, 58:544–552.

Pottmann, H. and Wallner, J. (2001). Computational line

geometry. Mathematics and Visualization. Springer,

Berlin.

Ravani, B. and Ku, T. S. (1991). Bertrand offsets of ruled

and developable surfaces. Computer Aided Design,

23(2):145–152.

Redonnet, J. M., Rubio, W., and Dessein, G. (1998). Side

milling of ruled surfaces: optimum positioning of the

milling cutter and calculation of interference. Ad-

vanced Manufacturing Technology, 14:459–463.

Senatore, J., Monies, F., Landon, Y., and Rubio, W. (2008).

Optimising positioning of the axis of a milling cutter

on an offset surface by geometric error minimization.

The International Journal of Advanced Manufactur-

ing Technology, 37(9-10):861–871.

Sprott, K. and Ravani, B. (1997). Ruled surfaces, Lie

groups and mesh generation. In 1997 ASME Design

Engineering Technical Conferences, Sacramento, Cal-

ifornia, USA.

Sprott, K. and Ravani, B. (2001). Kinematic generation of

ruled surface. Advances in Computational Mathemat-

ics, 17:115–133.

Sprott, K. and Ravani, B. (2007). Cylindrical milling of

ruled surface. The International Journal of Advanced

Manufacturing, 38(7-82):649–656.

Sprott, K. S. (2000). Kinematically generated ruled sur-

faces with applications in NC maching. PhD thesis,

University of California, Davis.

Zhou, Y. (2010). Optimization with Ruled Surface. PhD

thesis, Universit

at der Bundeswehr M

unchen.

Zhou, Y., Schulze, J., and Sch

afﬂer, S. (2009). Flank mill-

able blade design for centrifugal compressor. In Pro-

ceedings of the Mediterranean Conference on Control

and Automation, pages 646–650, Los Alamito, CA,

USA. IEEE Computer Society.

Zhou, Y., Schulze, J., and Sch

afﬂer, S. (2010). Blade ge-

ometry design with kinematic ruled surface approx-

imation. In SAC ’10: Proceedings of the 2010 ACM

Symposium on Applied Computing, pages 1266–1267,

New York, NY, USA. ACM.

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications