THE EFFECTS OF MARKET DEMAND ON TRUTHFULNESS
IN A COMPUTING RESOURCE OPTIONS MARKET
Owen Rogers and Dave Cliff
Department of Computer Science, University of Bristol, Merchant Venturers Building, Bristol, U.K.
Keywords: Market-oriented computing, Resource reservation, Risk assessment, Utility computing.
Abstract: Grid, cluster and cloud computing provide the opportunity for computing resources to be traded as
commodities in an open marketplace. An options market for computing resources would allow users to
reserve a resource for a fee, and then pay an additional fee later should they actually need to use it.
However, a major issue is ensuring that users do not falsify their likely requirements with the objective of
reducing costs while keeping their right to use the resource. This paper describes an exploratory simulation
implementation of a two-period model that was proposed by Wu, Zhang and Huberman (2008) which they
claimed promoted truth-telling among the population of resource-buyers who interact with a Coordinator (a
central vendor) of resources. Wu et al. provided a theoretical description and analysis of their model, but
presented no empirical analysis of its commercial suitability. Our work, reported in this paper, explores the
model's performance where demand for resources is variable and unpredictable. Using techniques similar to
replicator dynamics (from studies of evolutionary processes in biology), we explore the behaviour of
heterogeneous buyer populations under different market conditions. Through empirical and theoretical
analysis, we determine the optimum honesty for which the Coordinator will most effectively prosper across
a range of market conditions, and show how this data can be used to protect against risk.
1 INTRODUCTION
Grid, cluster and, most recently, cloud computing
have all promised to transform computing resources
into a commodity, that can be delivered in a manner
similar to that of existing utilities, such as electricity,
gas, water and telephone services (Buyya, Yeo et al.
2009). Cloud computing in particular is primed to
deliver a new level of freedom to the consumer,
allowing different levels of service and quality to be
delivered on an as-needed basis without the need for
capital investment.
This utility model provides users with the ability
to purchase computing resources as if they were any
other commodity such as coal or steel. By providing
a suitable mechanism for buying and selling, market
oriented computing opens up a wide range of trading
possibilities - CPU cycles, storage capacity, or
memory allocations can be bought and sold, for
current or future use. This is already happening to
some extent in the market place, and a wide range of
economic and resource sharing models for grids,
clusters and clouds are publicly accessible. (Yeo and
Buyya 2006; Hilley 2009)
However, the variable nature of IT usage means
that pricing the service so that competitiveness and
profitability are balanced has an element of risk. For
the enterprise, determining and hedging their future
demand for a resource is not an easy task. (Khajeh-
Hosseini, Sommerville et al. 2010)
Currently, users purchase capability from the
utility-computing provider directly: the use of
centralised computing marketplaces and
intermediary aggregators and brokers seem likely to
grow in significance over time but have not yet done
so.
Such centralised mechanisms would enable a
true Service Orientated Architecture where customer
needs are matched to the most suitable computing
resources using brokers or Coordinator’s. This
would be controlled through Service Level
Agreements (SLA) which would define the metrics
that must be achieved (e.g. uptime, latency) and the
compensation that would be due to the customer
should the metric not be achieved.
To take account of future requirements for
resource, users could reserve resources through a
derivatives market involving futures and/or options.
330
Rogers O. and Cliff D..
THE EFFECTS OF MARKET DEMAND ON TRUTHFULNESS IN A COMPUTING RESOURCE OPTIONS MARKET .
DOI: 10.5220/0003276003300335
In Proceedings of the 3rd International Conference on Agents and Artificial Intelligence (ICAART-2011), pages 330-335
ISBN: 978-989-8425-41-6
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

A futures contract is a contractual agreement to buy
or sell an asset for a certain price at a certain time in
the future. An options contract gives the contract
holder the right to buy, or sell, an asset by a certain
date for a certain price, without obligation. (Hull
2005)
It has been proposed that swing options,
originally developed for trading electrical power,
can be used to price a future reservation of
computing resources (Clearwater and Huberman
2005). Analogous to electricity, computing resources
are non-storable and have volatile usage patterns, so
such a model would provide customers with
flexibility in terms of amount and duration of
resource requirement, and enables resource
providers to estimate demand.
Use of such derivatives presents two problems.
Firstly, how can users accurately predict their future
resource requirement. Secondly, how can the user be
trusted to submit a true representation of their likely
resource requirements.
The first issue can be solved using a forecasting
tool, such as that proposed in (Clearwater and
Huberman 2005) or by analysing historical market
data such as that proposed in (Sandholm, Lai et al.
2006; Sandholm and Lai 2007). For the second
issue, (Wu, Zhang et al. 2008) proposed a
reservation model which was shown to lead to a
truthful reservation on the user's part.
In (Rogers and Cliff 2010) we simulated the
reservation model proposed by Wu et al., in a
multiple user, heterogeneous, variable market. Wu et
al.'s model involved a number of users who require
the resource, plus a central authority ("the
Coordinator") responsible for receiving and
resolving resource requests. We showed that honesty
benefits both the user and the Coordinator when the
market varies uniformly, and that the user-base
evolves to be more honest over time. In the same
paper, we discussed how the model could be
implemented commercially, and how a transaction
fee could be used to offset risk.
In this paper we extend our previous work by
exploring results from simulating the model when
the market has heterogeneous (non-uniform)
variations, and where the users make decisions
based on scarcity or abundance of resources. We
simulate various market conditions, and analyse how
the Coordinator and users behave as a result of this
changing dynamic. Finally, we discuss how our
findings can be used to protect against risk in a
commercial implementation.
We will look at the specific case analysed by Wu
et al. where the value of two key parameters are C=2
and k=1.5. The parameter C is the cost per unit paid
to the resource-providers by the Coordinator in the
second (future) period; the cost per unit is 1 when
purchased in the initial (current) period. The
parameter k is a constant that is used to set the price
per unit charged by the Coordinator to the resource-
users. Exploring this case is most attractive in the
first instance because it allows us to explore the
extent to which the results from Wu et al.’s
theoretical analysis continue to hold as some of their
simplifying assumptions are relaxed. Our primary
research question is to see whether the service
remains profitable in a real-world, multi-user
scenario, where users submit different resource
probabilities using different levels of honesty, in a
dynamically changing marketplace. It is this
heterogeneity of user’s behaviour under different
circumstances that makes our simulation an
extension of the theoretical model and supporting
analysis provided by Wu et al.
2 METHODOLOGY
A computer simulation was implemented in Python
to replicate the model as an options contract. The
algorithm performs the following steps:
1. Each user i in the range 1 to N is assigned an
"honesty", H
i
, chosen randomly from a uniform
distribution over [0,1] which describes the accuracy
with which a probability of future resource
requirement is provided to the Coordinator. An
honesty of 1 means a user will always exercise their
right to purchase as per their forecast probability. An
honesty of 0 means a user will never exercise their
right to purchase.
2. A replicator dynamics approach is adopted,
whereby for every two units of total time T, a user is
randomly chosen to undergo a mutation, and this
user is given a new honesty. The user tries bidding
and executing as per the following steps for a sample
size S, using the new honesty.
a. For each user, a random resource probability, p
i
,
is assigned. A probability of 0 means that a resource
will definitely not be required in the next time
period. A resource probability of 1 means a resource
will definitely be required in the next time period.
b. Each user is given the opportunity to request a
resource to be utilised in the next time period. The
user will submit the following resource probability
to the Coordinator: q
i
= H
i
p
i
c. The user is charged a premium of kq
i
2
/
2
to
THE EFFECTS OF MARKET DEMAND ON TRUTHFULNESS IN A COMPUTING RESOURCE OPTIONS MARKET
331

reserve the resource. The premium and a fixed
transaction fee, F, are removed from the user's bank
balance, and added to the Coordinator's balance.
d. The Coordinator purchases units from the
resource provider at a cost of 1 per unit. This is
removed from the Coordinator's balance and added
to the resource provider’s balance. As an example, a
user i with H
i
= 1 who anticipates the future
requirement with a probability of 0.8, will submit a
probability of 0.8 to the Coordinator as q
i
= H
i
p
i
e. A user i with H
i
= 1 will not always exercise
their right as per their submitted probability. For
instance, a user with honesty 0.7 who anticipates the
future resource requirement with a probability of
0.8, will submit a probability of future resource
requirement with q
i
= H
i
p
i
= 0.56.
f. Each user is now given the option of exercising
their right to use their resource.
g. A user will exercise their right where p
i
> A
where A is the availability of the resource. An
availability of 0 means that there is no surplus of the
resource and all users will exercise their right. An
availability of 1 means that that the resource is
abundant, and no users will exercise their right.
h. A is chosen randomly from a triangular
distribution, where the peak frequency of the
triangle is varied to show different market
conditions. An increase in the peak of the triangular
distribution represents an increase in the availability
of the resource - the increased frequency of random
values chosen at the peak of the triangle simulate a
variable market, which is biased towards either a
resource scarcity or abundance. A
p
is the peak and
A
m
is the mean of the distribution.
i. If a user wishes to use the resource, they are
charged a price, 1+(k/2)-kq
i
, which is removed from
their balance and added to the Coordinator's balance.
j. If the Coordinator has not previously purchased
enough resource from the resource provider, they
will purchase the deficit at a cost of C per unit.
k. This cost is removed from the Coordinator's
balance and added to the resource providers.
3. Steps a-k are repeated S times, to ensure each
user provides a range of probabilities to the
Coordinator using the same honesty.
4. If the user finds that the mean cost per required
resource over the sample S is lower using the
mutated honesty, the honesty remains and the new
behaviour is adopted by the user. If not, the honesty
returns to its previous value and the old behaviour
continues.
5. A new mutation is determined as per Step 2, and
this process continues until T iterations have passed.
3 RESULTS
The simulation was executed with F=0.01,
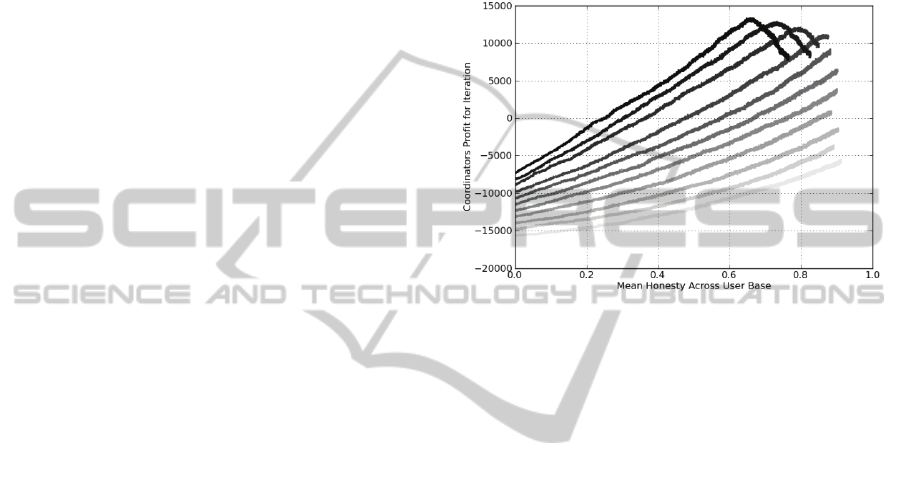
N=1000, S=100 and T=20000. See Figure 1.
Figure 1: Scatter plot of Coordinator’s profit against mean
honesty (legend in Table 1).
As can be seen from Figure 1, the Coordinator
generally benefits with increased profit when there is
a higher availability for resources and therefore
demand is low, although the amount of profit or loss
is still dependent on the mean honesty of the users.
This makes sense, as users have paid a premium
and a fee to use the service, but have not chosen to
execute their right due to the availability of cheaper
resources on the open market.
When the market is in high demand for
computing resources, the Coordinator will benefit
from increased profit as a result of increased mean
user-base honesty. However, the Coordinator will
often never make a profit regardless of the honesty
of the user-base. In these situations, the Coordinator
would be better off suspending sales completely or
implementing a higher transaction fee (see our
discussion of Dynamic Risk Offsetting, below).
However, when the availability of resources is
high there appears to be a point where profit no
longer increases with an increase in honesty, but
peaks at an optimum honesty where the Coordinator
achieves a peak profit.
Figure 2 shows the surplus/deficit of resource
purchased by the Coordinator in T=2 at the higher
rate of C=2. It can be seen that there is a correlation
between the values of H at which the peak profit
occurs in Fig. 1 and the values of H at which there is
no surplus or deficit of resource purchased in Fig. 2.
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
332

Figure 2: Best fit plot of resource surplus (legend Table 1).
If the Coordinator reserves too much resource in
T=1, they have effectively purchased assets that are
fully depreciated in T=2 and the investment has
gone to waste. If the Coordinator purchases too little
resource, they must purchase further resource in
T=2, now at the higher rate of C=2.
Thus, the optimum mean honesty of a user-base is
the honesty at which there is no surplus or deficit of
resource purchased by the Coordinator. As the
surplus is equal to the difference between the
resource required at T=2 and the resource reserved
at T=1, we can write:
Table 1 shows how the results obtained from
simulation closely match that determined using the
above formula when P
bar
=0.5.
Table 1: Table of results.
A
p
A
m
Honesty at
Peak Profit
(Sim)
Honesty at
Peak Profit
(Calc)
Graph
Legend
1.00 0.66 0.64 0.68
0.90 0.63 0.72 0.74
0.80 0.60 0.80 0.80
0.70 0.57 0.86 0.86
0.60 0.53 - 0.94
0.50 0.50 - 1.00
0.40 0.47 - 1.06
0.30 0.43 - 1.14
0.20 0.40 - 1.20
0.10 0.36 - 1.28
0.00 0.33 - 1.34
When there is poor availability of a resource, the
results show the Coordinator may make a loss in a
dishonest user-base as users are more likely to
execute their options, causing a deficit which must
be purchased at the higher value C=2.
When considering implementing the model in a
new market, the Coordinator must make a decision
regarding whether it is strategically better to
compete in a market where the user-base always
shows an increasing profit for an increase in honesty
(for example, as in A
m
= 0.53) albeit for less profit,
or where there is more demand for a resource, but a
decline in profit may occur once a certain level of
honesty has been reached by the user-base, as in
A
m
=0.6.
4 PRACTICAL APPLICATIONS
4.1 Maximising Profit
through Honesty Balancing
The simulation has shown how during times of low
demand, the Coordinator’s profit peaks at a certain
level of honesty across the user-base. If we want to
maximise the profit during this time, it should be
possible to develop an algorithm which balances the
user-base such that this peak honesty is achieved.
For example, consider the situation where at
T=1, the mean availability of the resource is A
m
=
0.53 and at T=2 the mean availability is predicted to
be A
m
=0.60. If users are submitting a mean
probability of 0.5 then it is straightforward to
calculate that at T=1, H
bar
=0.94; and at T=2, H
bar
=0.80. Thus, at T=1, the Coordinator will make a
maximum profit when 94% of the user-base is
honest. However, at T=2 the Coordinator will make
a profit when 80% of the user-base are honest. To
maximise the Coordinator’s profit, the mean honesty
of the user-base should be lowered to 80%. To
achieve this we propose that there should be an
ongoing process of monitoring and recording the
average honesties of all users over time. Once
gathered, analysis of this data in terms of sector,
industry, location, and any other classifications
should be done as required. This would then allow
the following process to be performed in each period
(i.e., at each successive value of T):
1. Determine mean market availability of market in
T=2, using methods such as discussed in (Sandholm,
Lai et al. 2006; Sandholm and Lai 2007)
2. Calculate H
bar
for which maximum profit is
achieved in T=2
THE EFFECTS OF MARKET DEMAND ON TRUTHFULNESS IN A COMPUTING RESOURCE OPTIONS MARKET
333

3. Using historical data and market intelligence,
determine which users or segments have an honesty
such that the optimum mean honesty can be
achieved.
4. Offer these users or segments a reduced
transaction fee as an incentive to purchase options as
a means of increasing or decreasing the mean
honesty of the user-base.
By incentivising users with a higher, or lower, mean
honesty it may be possible to move the overall
population mean to the optimum in T=2. This is one
avenue of future research that we aim to explore.
4.2 Dynamic Risk Offsetting
As discussed in Rogers & Cliff (2010), it is possible
for the Coordinator to protect herself against risk by
charging an appropriate transaction fee. The new
results presented in this paper show that the risk can
be further offset by anticipating market demand in
T=2 and charging an appropriate transaction fee.
It seems plausible that data-mining may establish
that a particular customer-base is more likely to be
dishonest. For example, one geographical region
may be less likely to be honest to a Coordinator in a
different geographical region due to previous
existing social, economic, political or cultural issues,
which causes an inherent lack of trust.
The term “honesty” can be here reasonably
interchanged with reliability. It may be that a
particular customer base has the best intentions, but
regularly reserve resources with an incorrect
probability. For example, a user who deals with
implementing complex systems may find it more
difficult to predict future usage accurately due to the
longer sales, implementation and acceptance cycles
brought about by determining complicated design
requirements. On the other hand, a particular
customer base may have a very accurate view of
future requirements, such as a website that has a
fixed number of users.
If the honesty of a particular segment is known,
the Coordinator may choose to charge a transaction
fee which varies with the market demand. Raising
the fee will increase the y-intercept of the profit
curve and therefore ensure a profit is achieved at
lower levels of honesty.
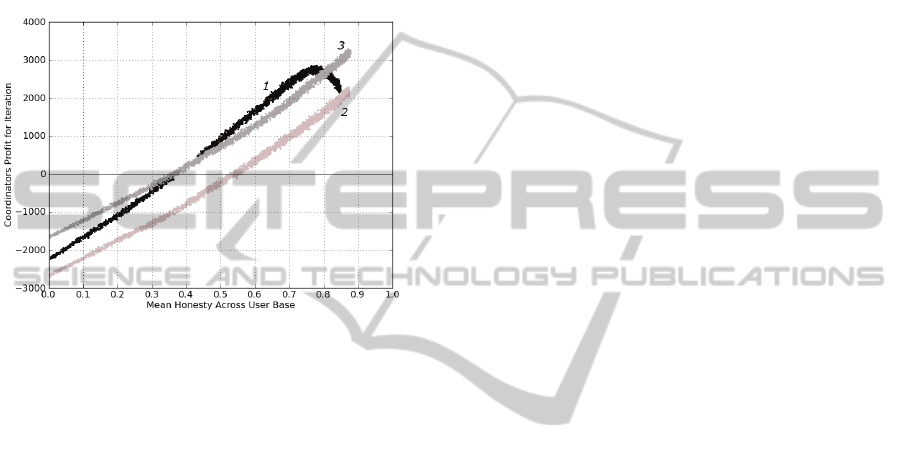
Figure 3 shows such an event, in which the user-
base has a mean honesty of 0.4 based on previous
experience for the sector:
1. During a period of high availability A
m
= 0.6, and
the Coordinator takes a profit.
2. It is predicted that in the next period, availability
will decrease to A
m
=0.53 and therefore demand will
increase. If the mean honesty of the user-base were
to remain constant, the Coordinator will make a loss.
3. To prevent this, the fee is raised to 0.05 which is
still insignificant compared to purchasing the
resource direct from the Coordinator (as C=2) but is
enough to offset this risk.
In fact, it may be possible to use the simulator in
real-time with predictive algorithms to counteract
the risk. Such an algorithm might look as follows:
1. Estimate demand for resources in T=2 using a
method such as those discussed in (Sandholm, Lai et
al. 2006; Sandholm and Lai 2007)
2. Estimate profit using the simulator, using
estimates for number of users, etc.
3. An appropriate transaction fee is determined to
offset any risk, which is presented to customers prior
to purchasing the option.
Further work should be undertaken to determine if
such inherent honesties/reliabilities exist in the
addressable market, and to determine a transaction
fee for each market segment such that risk and
competitive pricing are balanced. This segment
specific, variable-market pricing could be a powerful
differentiator.
5 CONCLUSIONS
This paper has provided an empirical demonstration
of how a truth telling reservation model for
computing resources described by Wu et al. can
provide the basis for a commercially feasible options
market in utility computing resources. The model
was simulated with multiple heterogeneous users,
submitting a wide range of probabilities over a long
term, over a variety of market profiles. It was found
that the Coordinator benefits more when resources
are in abundance, and less when resources are scare.
However, it was also found that when resources are
abundant, the Coordinator does not always benefit
financially as the honesty of the user-base increases.
There is an optimum honesty, which can be
determined from a simple equation, at which the
Coordinator’s profit is at a maximum.
The simulation has identified two methods that
can optimise the Coordinator’s profit, and reduce her
exposure to risk. The first is to bias the honesty of
the user-base towards the optimum honesty for a
predicted market demand by incentivising those
users who have a desired honesty. The second is to
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
334

vary the transaction fee payable by the user, to offset
predicted changes in market demand.
By taking the results from this paper and
extending them with future research into the
performance of the model under different conditions
and inherent honesties, in different segments, a
commercial offering that is profitable to the
Coordinator, beneficial to the user, and with
calculable levels of risk looks likely to be
achievable.
Figure 3: Example of risk offsetting procedure.
ACKNOWLEDGEMENTS
We thank the UK EPSRC for funding this research
as part of the Large-Scale Complex IT Systems
Initiative (www.lscits.org), as well as HP Labs
Adaptive Infrastructure Lab for providing additional
financial support.
REFERENCES
Buyya, R., C. S. Yeo, et al. (2009). "Cloud computing and
emerging IT platforms: Vision, hype, and reality for
delivering computing as the 5th utility." Future
Generation Computer Systems 25: 599-616.
Clearwater, S. H. and B. Huberman (2005). "Swing
Options: A Mechanism for Pricing IT Peak Demand."
Proceedings of 11th International Conference on
Computing in Economics.
Hilley, D. (2009). "Cloud Computing: A Taxonomy of
Platform and Infrastructure-level Offerings Cloud
Computing: A Taxonomy of Platform and
Infrastructure-level Offerings." Technology.
Hull, J. C. (2005). Fundamentals of Futures and Options
Markets.
Khajeh-Hosseini, A., I. Sommerville, et al. (2010).
"Research Challenges for Enterprise Cloud
Computing." Arxiv preprint.
Rogers, O. and D. Cliff (2010). "The Effects of
Truthfulness on a Computing Resource Options
Market." 1-6, ADPC'10 Proceedings.
Sandholm, T. and K. Lai (2007). "A statistical approach to
risk mitigation in computational markets."
Proceedings of the 16th international symposium on
high performance distributed computing 2007.
Sandholm, T., K. Lai, et al. (2006). "Market-based
resource allocation using price prediction in a high
performance computing grid for scientific
applications." HPDC'06: Proceedings.
Wu, F., L. Zhang, et al. (2008). "Truth-telling
reservations." Proceedings of 11th International
Conference on Computing in Economics.
Yeo, C. S. and R. Buyya (2006). "A taxonomy of market-
based resource management systems for utility-driven
cluster." Cluster Computing: 1381-1419.
THE EFFECTS OF MARKET DEMAND ON TRUTHFULNESS IN A COMPUTING RESOURCE OPTIONS MARKET
335