AUTOMATIC REMOVAL OF SPARSE ARTIFACTS IN
ELECTROENCEPHALOGRAM
Petr Tichavsk
´
y, Miroslav Zima
Institute of Information Theory and Automation, Pod vod
´
arenskou v
ˇ
e
ˇ
z
´
ı 4, Prague, Czech Republic
Faculty of Nuclear Science and Physical Engineering, Czech Technical University in Prague, Prague, Czech Republic
Vladim
´
ır Kraj
ˇ
ca
Faculty Hospital Na Bulovce, Bud
´
ınova 2, 182 00 Praha 8, Czech Republic
Czech Technical University in Prague, Faculty of Biomedical Engineering, Prague, Czech Republic
Keywords:
Artifact removal, Electroencephalogram, Independent component analysis, Second-order blind identification.
Abstract:
In this paper we propose a method to identify and remove artifacts, that have a relatively short duration, from
complex EEG data. The method is based on the application of an ICA algorithm to three non-overlapping
partitions of a given data, selection of sparse independent components, removal of the component, and the
combination of three resultant signal reconstructions in one final reconstruction. The method can be further
enhanced by applying wavelet de-noising of the separated artifact components.
1 INTRODUCTION
Methods of the Independent Component Analysis
(ICA) have been shown to be very useful in analyzing
biomedical signals, such as EEG and MEG, see e.g
Makeig et al, 1996, Vigario, 2000, Joyce and Gorod-
nitsky, 2004, or James, 2005. In particular, it ap-
pears that these methods have an ability to separate
unwanted parasitic signals (artifact), that have a rela-
tively simple structure, from the useful biological sig-
nals, which are rich in information.
ICA/BSS methods usually use either non-
Gaussianity, nonstationarity, a spectral diversity, or a
combination of the three. In our paper, the artifact in-
dependent components are, by definition, sparse, and
in the statistical sense this means that they are both
nonstationary and non-Gaussian. Sometimes the ar-
tifact components also have a typical signature in the
spectral domain. Therefore, any of the principles can
be used to separate the sparse sources (artifacts), but
not all methods have the same performance.
In the EEG signal processing, the most widely
studied ICA algorithms are Infomax of Makeig et al
(1996), SOBI of Belouchrani et al (1997), and Fas-
tICA of Hyv
¨
arinen and Oja (1997). While SOBI is
based on the second-order statistics, the other two al-
gorithms use high-order statistics. SOBI was advo-
cated by Romero (2008). In this paper, we mostly
use an algorithm BGSEP, proposed by Pham and Car-
doso (2001) implemented according to the paper of
Tichavsky and Yeredor, 2009. BGSEP is based on
second-order statistics as SOBI is, but it uses the non-
stationarity of separated signals. While SOBI is done
by approximate joint diagonalization (AJD) of a set
of time-lagged covariance matrices of the signal (the
mixture), BGSEP performs an AJD of zero lag co-
variance matrices in a partition of the signal.
In the context of the artifact removal it is desir-
able to have unwanted signals concentrated in a few
separated components. The original data can be re-
constructed without the artifact components using the
estimated mixing matrix.
The artifact that we want to identify and separate
have one common feature known as the sparsity in
the time domain. This topic is elaborated on in Sec-
tion II. The sparse artifacts include eye blinking and
other ocular artifacts, various movement artifacts and
unstuck electrode artifacts. The strong part of the pro-
posed method consists of a robust combination of par-
tial reconstructions obtained by processing mutually
overlapping epochs of the EEG recording. Like the
method of Castellanos and Makarov (2006), the pro-
posed method aims to obtain a high quality of artifact
removal at a negligible distortion of the cerebral EEG.
530
Tichavský P., Zima M. and Kraj
ˇ
ca V..
AUTOMATIC REMOVAL OF SPARSE ARTIFACTS IN ELECTROENCEPHALOGRAM.
DOI: 10.5220/0003276505300535
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2011), pages 530-535
ISBN: 978-989-8425-35-5
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

2 ARTIFACT REMOVAL IN ONE
EPOCH
For the purpose of designing and testing artifact re-
moval algorithms, we have considered three models
of artifacts that are shown in Figure 1. These artifacts
are inserted in an artifact-free EEG data at random
times and in randomly chosen channels as shown in
Figure 2. The models represent an eye blink, a body
movement, and an unstuck electrode.
8
7
6
5
4
3
2
1
Time [s]
250
+−
µV
Figure 1: Models of artifacts.
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
8
7
6
5
4
3
2
1
Time [s]
250
+−
µV
Figure 2: Example of neonatal EEG data with three embed-
ded artifacts.
All artifacts under the consideration have one fea-
ture in common: their duration is short compared
to the chosen epoch length. Such artifacts or sig-
nal components will be called sparse in the time do-
main. Usually, in the so called compressive sensing,
the sparsity is measured as the count of the time in-
stants in which the signal magnitude (absolute value)
exceeds certain threshold. However, there is a prob-
lem in how large this threshold should be.
In this paper, we propose a simple ad hoc defini-
tion of the sparsity, which appears to perform well in
our application. It is
sparsity(s
( j)
) =
max[|s
( j)
i
|]
std[s
( j)
i
]
log
std[s
( j)
i
]
median[|s
( j)
i
|]
!
(1)
where s
( j)
= (s
( j)
1
,...,s
( j)
N
) is the j−th independent
component, “std” stands for a standard deviation, and
i is the time index, and N is the number of samples in
the epoch. Note that the independent components are
10
+−
µV
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
8
7
6
5
4
3
2
1
Time [s]
Figure 3: Independent component obtained by BGSEP for
data in Figure 2. Sparsity (1) of the components is 115.2,
2.1, 1.4, 0.9, 3.2, 3.9, 42.0, and 7.7, respectively.
usually normalized to have the variance equal to one,
so that std[s
( j)
i
] = 1. The definition is motivated by the
fact that the sparse components have large maximum
absolute value, and simultaneously the median of the
absolute value should be close to zero. We note, how-
ever, that the choice of the criterion of the sparsity is
not crucial for our method, and our criterion can be
easily replaced by another user-chosen criterion and a
corresponding sparsity threshold.
For any definition of the sparsity, the component
is regarded to be sparse (artifact), if its sparsity ex-
ceeds some threshold. The threshold is a design vari-
able of the proposed artifact removal procedure. A
higher value of the limit means a more conservative
(a weaker) artifact reduction.
For example, independent components obtained
by applying the algorithm BGSEP, and their sparsities
(1) are shown in Figure 3. Note that the components
1, 6 and 7 have the largest sparsity and represent the
separated artifacts. The figure suggests that the spar-
sity threshold should be set about five.
Since each artifact occupies one independent com-
ponent, the number of artifacts in one epoch is upper
bounded by the number of channels
1
. Therefore, the
proposed method cannot remove many artifacts in one
time window, but only a few.
Among the independent components produced by
an ICA algorithm, those with a sparsity exceeding a
threshold are considered an artifact. In the reconstruc-
tion step, these components are replaced by zeros, and
the reconstructed signal is computed by multiplying
the matrix of the components by the estimated mix-
ing matrix.
A detailed comparative study of the most popular
ICA/BSS methods in terms of their ability to sepa-
rate artifacts in EEG data was published in Delorme,
2007. Our simulations, not included here for lack of
space show that the algorithm BGSEP also performs
very well. Moreover, this method is very cheap com-
1
It is admitted that one artifact may affect several chan-
nels, but it must have the same shape in all channels.
AUTOMATIC REMOVAL OF SPARSE ARTIFACTS IN ELECTROENCEPHALOGRAM
531

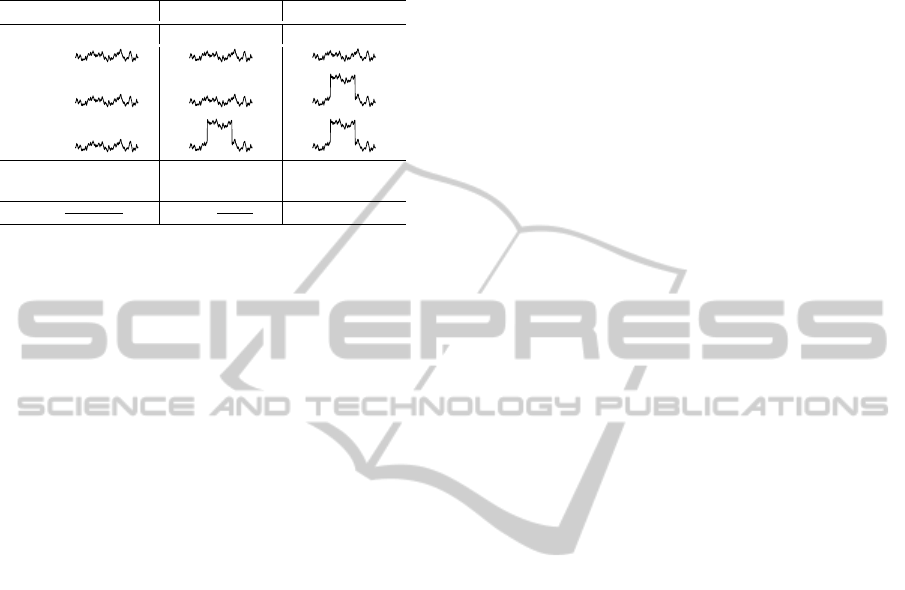
Table 1: Three cases that may occur in combining three
partial reconstructions in one (plus their permutations),
where ρ
i j
= kr
i
− r
j
k
2
, µ
i
= max|r
i
|, i, j = 1,2,3, ρ
max
=
max{ρ
i j
}, ρ
min
= min{ρ
i j
}, µ
min
= min{µ
i
}.
case A case B case C
r
1
r
2
r
3
ρ
max
≤ 2ρ
min
or ρ
max
≤ 2ρ
r
µ
3
> µ
min
ρ
12
= ρ
min
µ
1
= µ
min
ρ
23
= ρ
min
f =
r
1
+r
2
+r
3
3
f =
r
1
+r
2
2
f = r
1
putationally.
Note that the artifact removal can be enhanced by
wavelet de-noising of the to-be removed artifact com-
ponents see Castellanos and Makarov, 2006. It has
the positive effect of less removal of cerebral activity
from the data.
3 ARTIFACT REMOVAL
IN MULTIPLE EPOCHS
The data records that are encountered in EEG data
processing are usually long. If the artifact removal is
performed simply epoch by epoch, the performance
may not always be satisfactory. Some artifacts can
fall into two adjacent epochs and are masked. To in-
crease robustness of the procedure, we found useful to
perform the artifact removal in multiple epochs three
times, each time with a different partitioning of the
data into epochs.
The first partitioning of the time is [1,N], [N +
1,2N], ..., [(n−1)N +1,nN], where N is the length of
the epochs and n is the number of the epochs. n can be
arbitrary. In the newborn EEG data, N is 1000-3000
samples, that is 10-20 seconds at 128 Hz or 256 Hz
sampling.
The second partitioning of the time is [1,N/3],
[N/3 + 1, 4N/3], .. ., [N/3 + (n − 2)N + 1,nN −
2N/3], [nN − 2N/3 + 1, nN]. The artifact removal
is performed only in the middle n − 1 epochs of the
length N. In the first and in the last intervals, no arti-
fact removal is performed.
The third partitioning is [1,2N/3], [2N/3 +
1,5N/3], .. ., [nN − 4N/3 + 1,nN − N/3], [nN −
N/3 + 1,nN]. Again, the artifact removal is per-
formed only in the middle n − 1 epochs of the length
N.
Each partitioning gives rise to one possible
artifact-free reconstruction of the whole data. These
reconstructions are combined together in a special
way so that the resulting reconstruction is generally
smoother and more artifact-free than the partial re-
constructions. An example of the three partitioning
and corresponding reconstructions together with a fi-
nal reconstruction is shown in Figure 5.
Combination of the three reconstructions into one
proceeds sequentially, channel by channel, in time
segments that are generally shorter than the epochs
with the application of the ICA. They may have the
form [(k − 1)T
s
+ 1,kT
s
], where T
s
is the length of the
segment (typically 200-300 samples).
Let r
1
, r
2
and r
3
denote the three partial recon-
structions in a channel in some (say the k-th) time
segment. Let ρ
i j
= kr
i
− r
j
k
2
denote the squared Eu-
clidean distances of the reconstructions, i, j = 1,2,3,
and let µ
i
denote the maximum absolute value of el-
ements of r
i
, i = 1,2,3. Let ρ
r
denote the average
squared norm krk
2
of a data segment r of the same
length as r
i
, randomly or systematically chosen in the
whole available data, and let f denote the desired fi-
nal reconstruction. The choice of f is summarized in
Table 1.
In short, some of the three reconstructions might
not be artifact-free and potentially still contain signifi-
cant residua of the artifact. This possibility is presum-
ably characterized by a relatively large µ
i
. Therefore
the proposed algorithm combines only “good” partial
reconstructions. Depending on values of ρ
i j
and µ
i
,
i, j = 1,2,3, f is obtained as the average of one, two,
or all three reconstructions.
4 SIMULATIONS
4.1 Removal of Artificial EEG Artifacts
In this subsection, performance of the proposed algo-
rithm is studied on a visually noise-free EEG data set
with five embedded artifacts, see figure 4a and 4b.
The proposed artifact removal procedure was
applied with ICA (BGSEP with parameter 10) was
computed in epochs of the length of 2500 samples
(≈ 20s). The time window for the reconstruction
had 256 samples (2s). The limit sparsity was set
to 3. Each artifact components was de-noised
using the Matlab wavelet toolbox, the command
wden(data,’minimaxi’,’s’,’one’,7,’sym5’),
prior its removal in each epoch and prior the synthesis
of the three reconstructions. The resultant cleaned
data and the estimated artifact (the noisy data minus
the reconstruction) are shown in Figures 4(b) and
4(c), respectively. We note that the artifact removal
is somewhat conservative, i.e. that the estimated
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
532

artifacts have a bit lower magnitude then the original
(this is good).
0 5 10 15 20 25 30 35 40 45 50
8
7
6
5
4
3
2
1
Time [s]
250
+−
µV
Figure 4(a): Original neonatal EEG data (a sleep).
0 5 10 15 20 25 30 35 40 45 50
8
7
6
5
4
3
2
1
Time [s]
250
+−
µV
Figure 4(b): The same EEG data with a few inserted arti-
facts.
0 5 10 15 20 25 30 35 40 45 50
8
7
6
5
4
3
2
1
Time [s]
250
+−
µV
Figure 4(c): Estimated artifacts (without WD).
0 5 10 15 20 25 30 35 40 45 50
8
7
6
5
4
3
2
1
Time [s]
250
+−
µV
Figure 4(d): Estimated artifacts (with WD).
0 5 10 15 20 25 30 35 40 45 50
8
7
6
5
4
3
2
1
Time [s]
250
+−
µV
Figure 4(e): Error of the reconstruction (without WD).
0 5 10 15 20 25 30 35 40 45 50
8
7
6
5
4
3
2
1
Time [s]
250
+−
µV
Figure 4(f). Error of the reconstruction (with WD).
We note that the error of the reconstruction, where
the wavelet denoising of the artifact was applied, was
greater than if it was absent.
4.2 Removal of Real EEG Artifacts
In this subsection, an example of performance of the
proposed algorithm for the removal of real artifacts
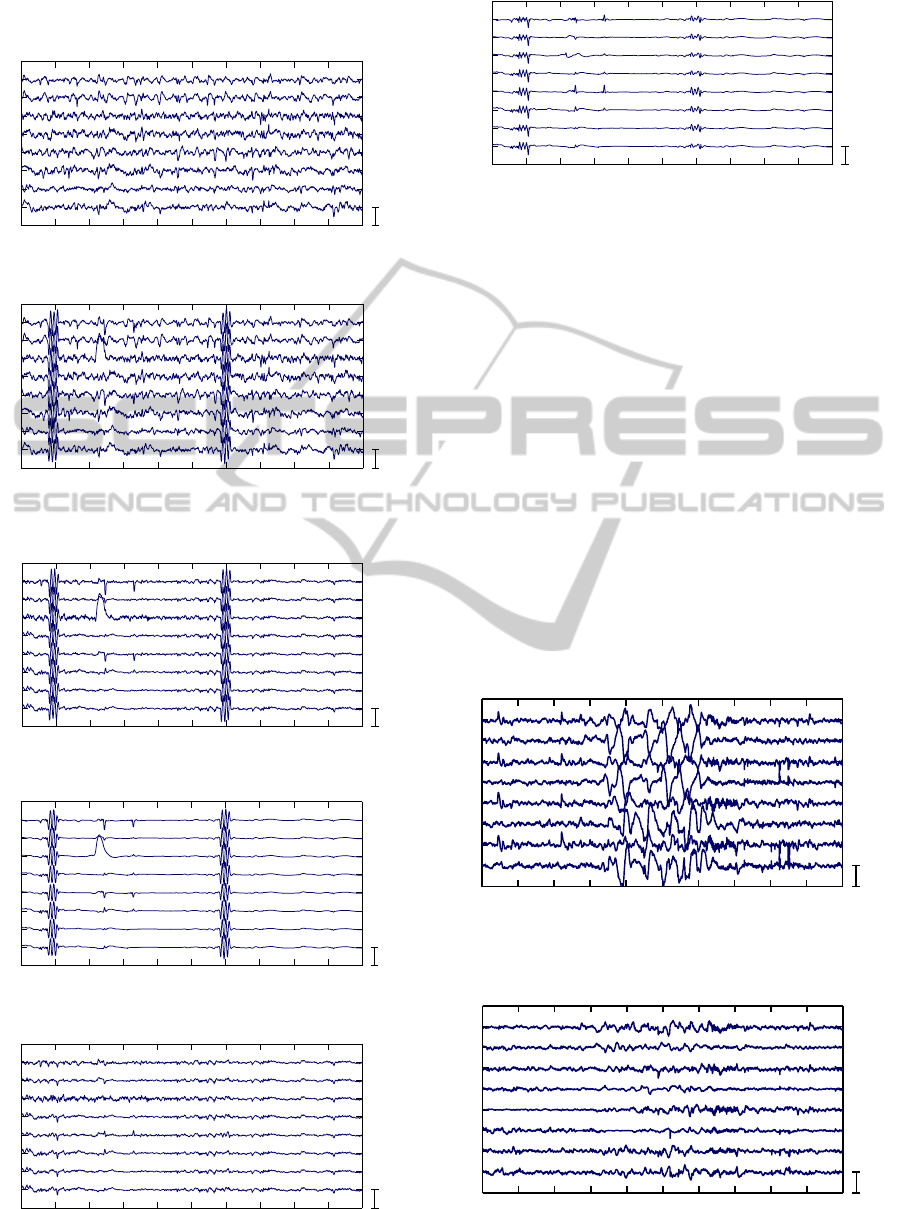
from EEG data is presented, see Figure 5(a). The
main difference is that the ground truth (artifact-free
signal) is not known. The EEG recording was sam-
pled by 128 Hz. The epochs for ICA analysis had
2500 samples (≈ 20s), and the time window for the
reconstruction had 256 samples (2s). The results are
shown in Figure 5(b)-(e). The three partial recon-
structions and a final reconstruction of the component
is shown in Figure 6. We note that not in all partial re-
constructions the artifacts were sufficiently well sup-
pressed, but the final reconstruction looks good.
0 5 10 15 20 25 30 35 40 45 50
8
7
6
5
4
3
2
1
Time [s]
250
+−
µV
Figure 5(a): Neonatal EEG data with real movement artifact
and eye blinking.
0 5 10 15 20 25 30 35 40 45 50
8
7
6
5
4
3
2
1
Time [s]
250
+−
µV
Figure 5(b): Removal of artifacts without WD.
AUTOMATIC REMOVAL OF SPARSE ARTIFACTS IN ELECTROENCEPHALOGRAM
533

0 5 10 15 20 25 30 35 40 45 50
8
7
6
5
4
3
2
1
Time [s]
250
+−
µV
Figure 5(c): Removal of artifacts with WD.
0 5 10 15 20 25 30 35 40 45 50
8
7
6
5
4
3
2
1
Time [s]
250
+−
µV
Figure 5(d): Estimated artifact (without WD).
0 5 10 15 20 25 30 35 40 45 50
8
7
6
5
4
3
2
1
Time [s]
250
+−
µV
Figure 5(e): Estimated artifact (with WD).
0 5 10 15 20 25 30 35 40 45 50
5
4
3
2
1
Time [s]
250
+−
µV
Figure 6: Three partial reconstructions of the 2nd channel
in Figure 5 (epochs for the single frame artifact removal
are marked by vertical lines), the final reconstruction, and
intervals used for combining the partial reconstructions in
one.
Note that the current implementation of the arti-
fact separation procedure, which exists either in Mat-
lab or in C++, allows processing a 10 minutes long 8
channel recording sampled at 256 Hz in about 10s on
an ordinary PC with a 3GHz processor.
5 CONCLUSIONS
The presented method of artifact removal from data
of arbitrary length is suitable for artifacts that have
relatively short duration and exceed in the magnitude
of the neighborhood signal. Examples include eye
blinks or occasional body movement artifacts. The
method is also fast in comparison with other ICA-
based methods, because it uses a computationally ef-
fective method BGSEP. Increased robustness of the
procedure is obtained by a sophisticated way of com-
bining three ICA reconstructions. The method can
be used, for example, as a data preprocessing for the
identification of sleep stages of neonatal babies, but it
is not limited to this kind of data. More details can be
found in Zima et.al. (2010).
ACKNOWLEDGEMENTS
This work was supported by Ministry of Education,
Youth and Sports of the Czech Republic through the
project 1M0572 and by Grant Agency of the Czech
Republic through the project 102/09/1278.
REFERENCES
Belouchrani A, Abed-Meraim K, Cardoso J.F., Moulines
E. (1997) A blind source separation technique using
second-order statistics. IEEE Transactions on Signal
Processing 1997; 45:434-444.
Castellanos NP, Makarov V.A. (2006) Recovering EEG
brain signals: Artifact suppression and wavelet en-
hanced independent component analysis. J. Neuro-
science Methods 2006; 158:300-312.
Delorme A, Sejnowski T., Makeig S. (2007) Enhanced
detection of artifacts in EEG data using higher-order
statistics and independent component analysis. Neu-
roimage 2007; 34:1443-1449.
Hyv
¨
arinen A., Oja E. (1997) A fast fixed-point algorithm
for independent component analysis. Neural Computa-
tion 1997; 9:1483-1492.
James C.J., Hesse C.W. (2005) Independent component
analysis for biomedical signals. Physiological Mea-
surements 2005; 26:R15-R39.
Joyce C.A., Gorodnitsky I.F., Kutas M. (2004), Automatic
removal of eye movement and blink artifacts from EEG
data using blind component separation. Psychophysiol-
ogy 2004; 41:313-325.
Makeig S., Bell A.J., Jung T.P., Sejnowski T.J. (1996) Inde-
pendent component analysis of encephalographic data.
Adv. Neural Inf. Process. Syst. 1996; 8:145-151.
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
534

Pham D.T., Cardoso J.F. (2001). Blind separation of in-
stantaneous mixtures of nonstationary sources. IEEE
Transactions on Signal Processing 2001; 49:1837-
1848.
Romero S., Mananas M., Barbanoj M. (2008), A compar-
ative study of automatic techniques for ocular artifact
reduction in spontaneous EEG signals based on clini-
cal target variables: A simulation case. Computers in
Biology and Medicine 2008; 38:348-360.
Tichavsk
´
y P., Yeredor A. (2009) Fast approximate joint
diagonalization incorporating weight matrices. IEEE
Transactions on Signal Processing 2009; 57:878-891.
Vigario R. (2000) Independent component approach to the
analysis of EEG and MEG recordings. IEEE Transac-
tions on Biomedical Engineering 2000; 47:589-593.
Zima M., Tichavsk
´
y P., and Kraj
ˇ
ca V. (2010) Automatic re-
moval of sparse artifacts in electroencephalogram, In-
stitute of Information Theory and Automation, Prague,
Czech Republic, Technical Report No. 2289, Novem-
ber.
AUTOMATIC REMOVAL OF SPARSE ARTIFACTS IN ELECTROENCEPHALOGRAM
535