GLOTTAL SOURCE ASYMMETRY ESTIMATION BY ICA

Pedro Gómez-Vilda, Roberto Fernández-Baíllo, Victoria Rodellar-Biarge

GIAPSI, Facultad de Informática, Universidad Politécnica de Madrid

Campus de Montegancedo, s/n, 28660 Boadilla del Monte, Madrid, Spain

Carlos G. Puntonet

Departamento de Arquitectura y Tecnología de Computadores, ETSII, Universidad de Granada

C/ Daniel Saucedo, s/n 18071 Granada, Spain

Keywords: Glottal Source Correlates, Independent Component Analysis, Pathology Detection, Voice Production.

Abstract: Healthy Voice Production and Voice Care are subjects of growing concern nowadays. Knowing that many

Voice Diseases result in asymmetric vibration, a method to estimate the percentage of asymmetry has been

developed on the Glottal Source obtained by the inverse filtering of Voice. The asymmetric biomechanics is

treated as a result of unknown sources which are separated using classical Independent Component

Analysis. The paper presents specific real cases and produce results which animate an open discussion on

the background underlying processes, which may be based on clear asymmetric biomechanics affecting

differently to each vocal fold as by the result of lesions or injuries in one or both of them. Results are

presented and conclusions derived.

1 INTRODUCTION

Glottal Signals are those related with the vibration of

the vocal folds in the production of voice. The

Glottal Source (GS) is the most used in the study of

Voice Pathology (Titze 1994) and in Voice

Biometry (Plumpe et al. 1999), among other fields.

The Glottal Source is considered an observable

correlate of the vocal fold vibration. It may be

estimated by inverse filtering the radiated voice,

which is captured by a microphone at a certain

distance of lips. It and can be associated with the

dynamic pressure developed in the near region of the

vocal folds as a consequence of the biomechanics

involved in their vibration. Therefore the Glottal

Source is taken as the basic signal for voice studies

nowadays. This signal is also considered the basic

excitation of the Vocal Tract producing voice as in

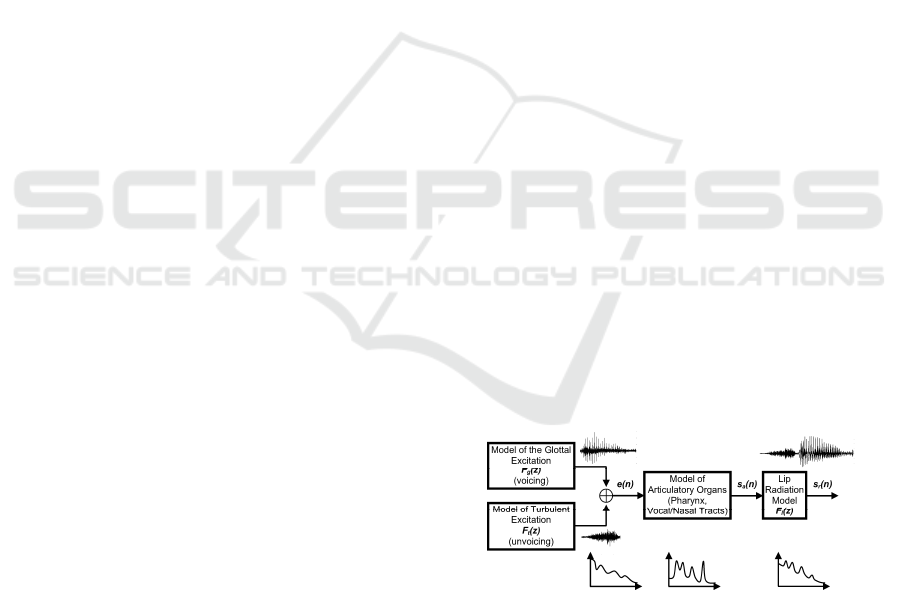
the well-known Fant's Production Model (Fant

1960) as in Figure 1. The typical time-domain

pattern shown by the Glottal Source obeys the cycle

shown in Figure 2 known as the Liljencrants-Fant

profile (Fant et al., 2004). As it is a pressure, its

static value is considered to be 1 (atmospheric

pressure in quiescent conditions).

Figure 1: The Voice Production Model of G. Fant. The

excitation may be glottal (voiced) or turbulent (unvoiced).

Voice studies assume the first case always.

The cycle starts at the closing instant (t=0), just

immediately after the (almost) complete stop of air

flow through the vocal folds. Due to the presence of

the air column moving out along the Vocal Tract,

and its inertial behaviour, the pressure drops to a

minimum (considered 0 here for normalization

purposes, see the thick full line). Some moments

later, the pull-back of the air column restores the

pressure to equilibrium (recovery point r). This

situation is maintained till the opening of the vocal

folds (o) were the sudden input of air flow from the

lungs raises the pressure to a maximum. The vocal

folds initiate a new closing cycle in (c), and the

pressure starts a decay as the flow stops to reach the

559

Gómez-Vilda P., Fernández-Baíllo R., Rodellar-Biarge V. and Puntonet C..

GLOTTAL SOURCE ASYMMETRY ESTIMATION BY ICA.

DOI: 10.5220/0003289805590564

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (MPBS-2011), pages 559-564

ISBN: 978-989-8425-35-5

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

minimum at the closure instant, and the cycle starts

again.

Figure 2: The LF Glottal Cycle. Top: In full black line the

GS Ideal pattern. Bottom: Real pattern obtained from a

prototype male speaker (normophonic).

Classically, distortions of the Glottal Cycle

relative to the L-F pattern are known to be related to

vocal fold pathology. Distortions imply changes

within the Glottal Cycle or changes among

neighbour cycles. These last have to see with

asymmetric vocal folds, and may be due to lesions

affecting a single vocal fold, as unilateral polyps,

cysts, sulci, paralisis, tumors, etc. (Dworkin and

Meleca 1997). Therefore, the detection and

measurement of vocal fold asymmetric vibration is

an important goal in the study of vocal fold

pathology.

The purpose of the present paper is to deepen in

the accurate measurement of vocal fold asymmetric

vibration. As good methods to rebuild the Glottal

Source from voice have been developed in the past

years (Bäckström et al., 2002) a possible way to face

the study of the asymmetry is to contrast neighbour

cycles as if they were produced by independent

unknown sources using Independent Component

Analysis (Hyvärinen et al., 2001).

The paper is divided into the following sections:

in section 2 a brief presentation of glottal source

biomechanics is given together with a hint on Glottal

Source reconstruction; section 3 is devoted to

present delayed versions of the Glottal Source as

produced by two independent unknown signals,

which have to be estimated in duration and

amplitude, from which the vibrations of each vocal

fold can be inferred; section 4 will be devoted to

produce biomechanical estimates of each

independent vocal fold and to infer their possible use

in asymmetry-base vocal fold pathology; finally in

section 5 conclusions will be presented.

2 ASYMMETRIC VOCAL FOLD

BIOMECHANICS

The vocal folds are soft tissues found in the larynx

supported by the cryco-thyroid cartilages as

illustrated in Figure 3.

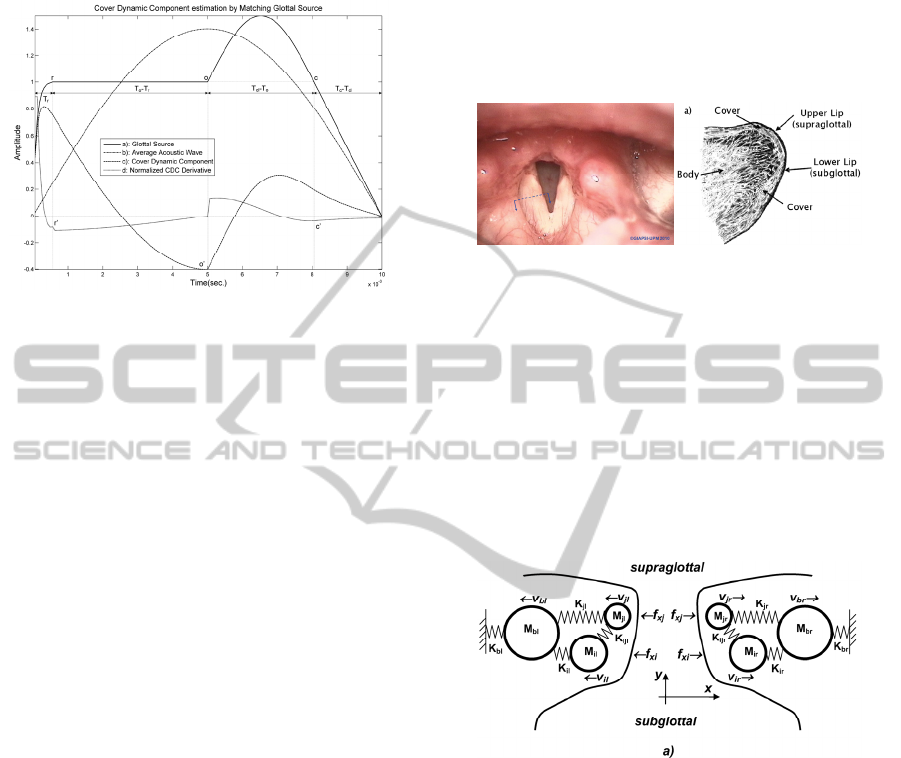
Figure 3: View of a typical Vocal Fold (left) and its

transversal section at the line drawn on the left vocal fold

(right).

The transversal section of the Vocal fold shows a

main muscle-type structure (the body or musculus

vocalis) surrounded by a mucosal epithelium-type

structure (the cover or lamina propria). Leaving

apart other more sophisticate models, the

biomechanics of the vocal folds is briefly

summarized after the presentation of the Story and

Titze 3-mass model (Story and Titze, 1995) shown

in Figure 4 below.

Figure 4: Vocal Fold Biomechanical Model of Story and

Titze (see text for details).

This model represents the balances among forces

acting on the different masses representing the body

and the cover. Classically a lumped mass (M

) is

enough to represent the body dynamics, whereas the

cover is divided in two different masses (M

, M

) to

reproduce the mucosal wave phenomenon (Berry

2002). These masses are linked by springs which

represent the elasticity of the bonding tissues (K

, K

). A certain degree of non-elastic loses are

associated to each spring as a mechanic resistance

, R

). The suffixes l,r refer to the left or

right vocal fold. Taking these conditions into

account the following would be the dynamic

biomechanical equations for the body and cover

masses:

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

560



()

ξξ

dvvKdvK

dvKdvK

rilrjlrijl

rjlrjl

rjl

rjlrjl

rjlrilrijl

rilril

ril

rilril

rjlrbjl

rilrbil

rblrbl

rbl

∫∫

∞−∞−

−+−

∂

−+−

∂

,,,,,

,,,,

(1)

where:



jl,rbl,r

rjl

il,rbl,r

ril

vvv

−=

(2)

refer to the difference between the body and the

respective cover mass velocities. This biomechanical

description is of most interest, as it may be used for

the indirect estimation of the biomechanical

parameters involved through transfer function fitting

(Gómez et al., 2009) provided that independent

estimates of the right and left glottal signals can be

obtained, as is the intention of the present study.

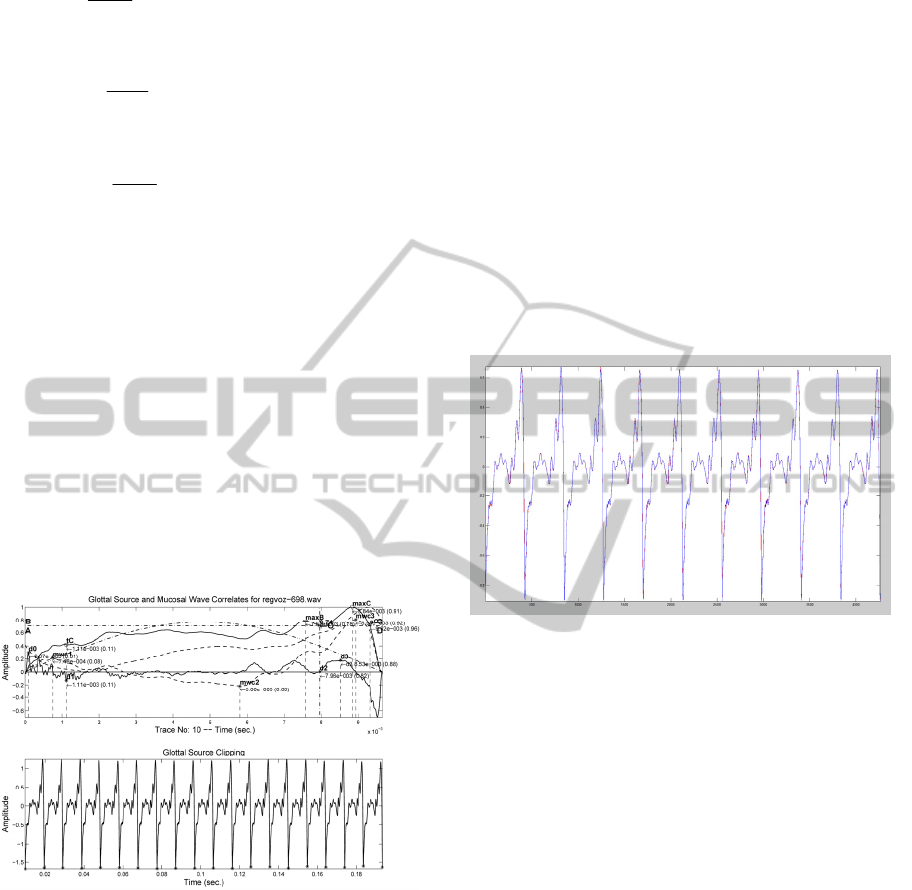
Figure 5: Reconstructed Glottal Source from voice. Top:

Single cycle. Bottom: Several phonation cycle sequence.

The reconstruction of the Glottal Source from

voice is based on inverse filtering of the voice trace

by means of adaptive lattice filters (Gómez et al,

2009). An example of a reconstructed glottal source

from voice is given in Figure 5.

3 SIGNAL SEPARATION BY ICA

The methodology of Independent Component

Analysis to be used in this work is rather classical

and well-known (Hyvärinën et al., 2001), yet

powerful and efficient, as will be shown in the

sequel. The intention of the present section is not to

deepen into ICA theory, but to give the necessary

details for a good comprehension on how ICA has

been used in the solution of the two-fold vibration

reconstruction. The starting hypothesis is that the

observable glottal source vibration cycle, if

asymmetric enough, is dominated either by one or

the other vocal fold dynamics, therefore a way to

extract information of any vibration differences

could be to confront the same vibration pattern

against itself time-drifted exactly in one glottal

cycle. For the pattern shown in Figure 5, confronting

exactly ten neighbour phonation cycles a match as

the one shown in Figure 6 below would be obtained.

Figure 6: Matching ten glottal cycles of the glottal source

in Figure 6 delayed exactly one cycle. The original trace is

given in blue, the delayed one is given in red. Differences

are minimal, indicating a stable normophonic phonation

(speaker 698).

The working hypothesis under ICA is that these

two signals, which will be referred as u

(n)

(original) and u

(n) (delayed) are observations

produced by two independent sources s

(n) and

(n) which are not directly observable in

themselves, but produced through a mixing matrix A

which is not known a priori as given by:

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

2221

1211

Asu

(3)

The classical procedure to apply ICA is to first

de-correlate the observations vector

u, then apply a

whitening process on the de-correlated observations

and finally evaluate an inversion matrix

optimizing a certain criterion based on a measure of

statistical independence. Practically speaking these

details are subsumed in the operation of the

mathematical package Fast-ICA due to Hyvärinen et

al (2001). The version 2.5 for MATLAB of the

referred package (see references) has been used in

GLOTTAL SOURCE ASYMMETRY ESTIMATION BY ICA

561

the present study. In this way the mixing matrix

and the unknown sources

s can be estimated in a

very agile way allowing to experiment with different

configurations as explained in the next section.

4 ASYMMETRY

ESTIMATION: RESULTS

One of the purposes of the present work is to explore

if ICA can be used in estimating independent

sources to explain the differences found in the

glottal source observed in neighbour phonation

cycles, therefore an example of a glottal source

exhibiting these differences was selected from a

less-normal speaker (others would say a more

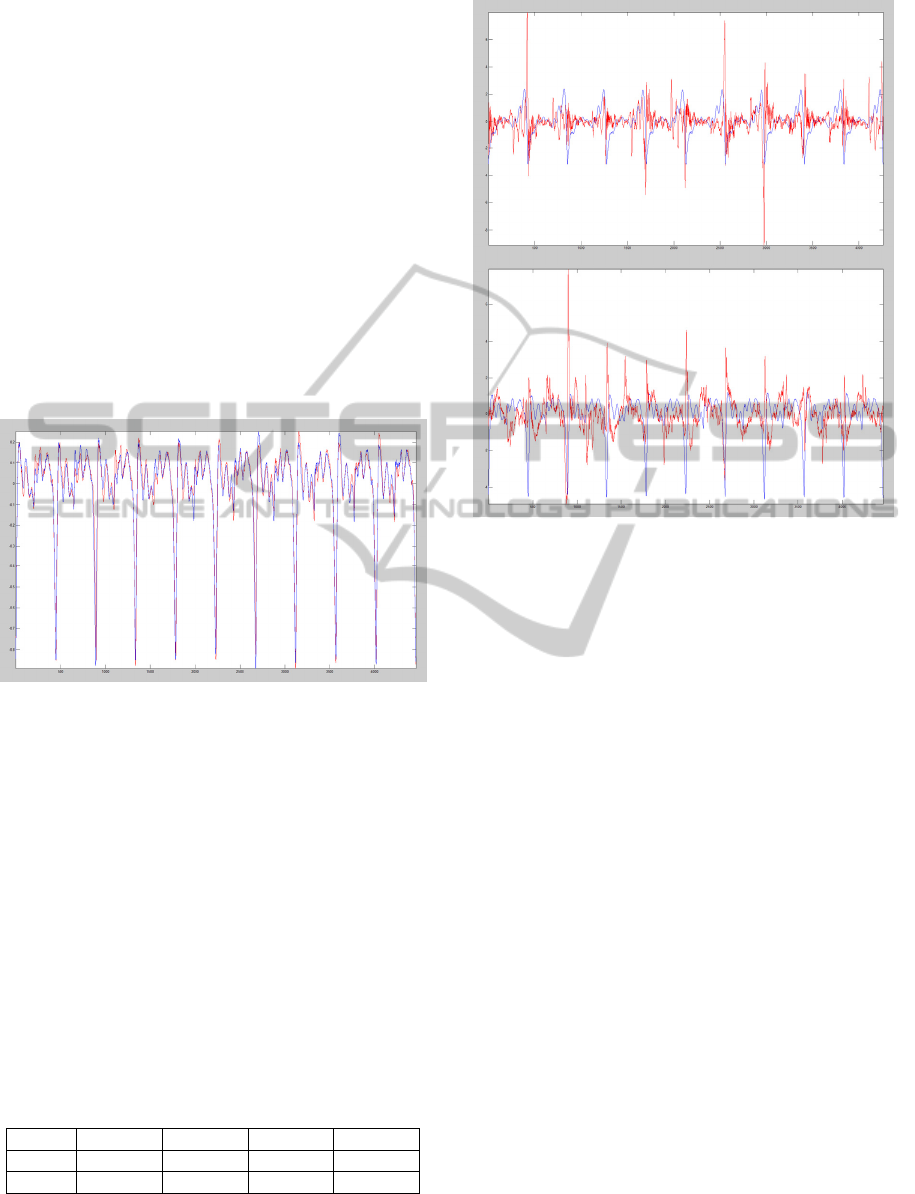
dysphonic, case 181) as the one in Figure 7 below.

Figure 7: Matching ten glottal cycles of a less symmetric

phonation, delayed exactly one cycle. The original trace is

given in blue, the delayed one is given in red. Differences

are clear in this case, indicating a less normophonic

phonation (speaker 181).

This figure shows a less classical glottal pattern,

and it may be seen that contrasting ten cycles of the

original and delayed series do show some

dissimilarities which may be clearly appreciated.

The purpose of this preliminary experiment will be

to apply ICA to these two sets of observations (the

ones in Figure 6 and Figure 7, respectively). The

nonlinear function used in the estimates was the

hyperbolic tangent (tanh). The table which follows

gives the estimates of the mixing matrix.

Table 1: Values of the mixing matrix coefficients for the

two series studied.

Coeff. a

Sp. 698 0.0096 0.2809 -0.0019 0.2811

Sp. 181 0.0193 0.1889 -0.0252 0.1877

The estimates of the independent unknown

sources are depicted in Figure 8 below.

Figure 8: Independent components for the cases studied.

Top: case 698, glottal source common mode in blue,

differential mode in red. Bottom: Id. for case 181.

It may be observed that one of the components

(in blue) resembles strongly the overall pattern of

the respective glottal source, whereas the other

component (in red) stresses mainly the differences

between neighbour cycles. Therefore these two

components will be referred as the common and

differential modes in the sequel. These figures do

not show the relative contribution of each

component to each observed trace. To stress this

comparison the independent components are to be

weighted by the respective mixing coefficients, to

produce the traces in Figure 9 below.

The comments to the results in the figures after a

first inspection offer some interesting hints

favouring the use of this methodology in further

studies of voice pathology. The common component

is the main contribution to the resulting observation,

especially in case 698, where the differential

contribution is almost irrelevant. This means that the

more symmetric the vibration, the larger the

common mode vs the differential one. The case 181

is different, as apparently the energy of the

differential component is much larger in this case.

Knowing in advance that case 181 is mildly

dysphonic whereas case 698 is typically

normophonic, the ratio between the energy of the

differential vs the common modes could serve as a

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

562

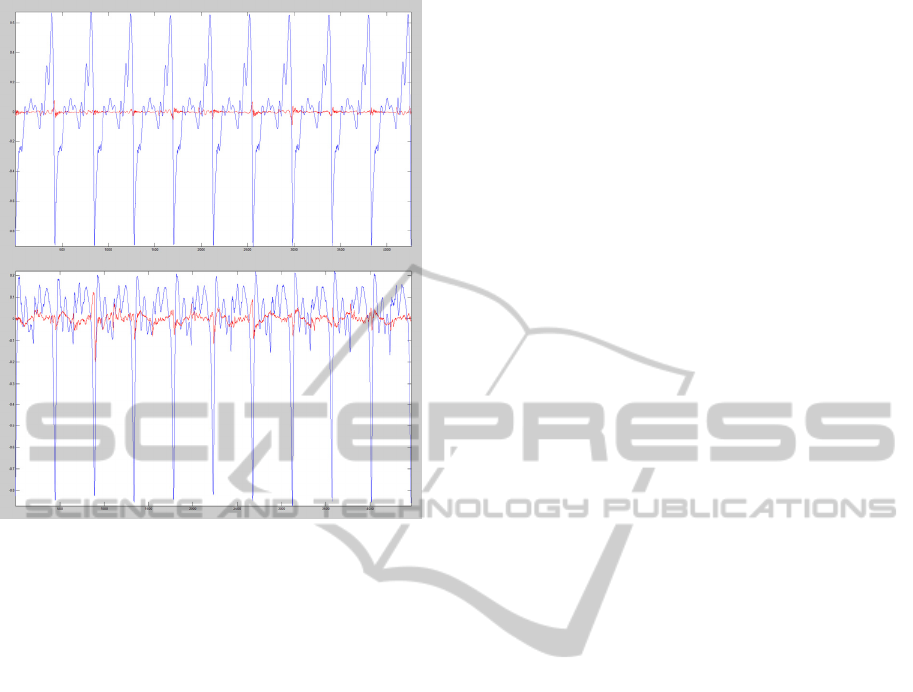
Figure 9: Contributions of each independent component to

(n) as weighted by the adequate mixing coefficients.

Top: case 698, glottal source common mode in blue,

differential mode in red. Bottom: Id. for case 181.

pathology index by itself. And these pathology

indices can be anticipated in advance: these are the

ratios between the coefficients of matrix

A, by rows.

Of course, this is simply a preliminary observation

which needs to be certified by a more exhaustive

study on a wider subset of the database from which

these two samples have been drawn. Without going

to a more exhaustive study, which is left for further

investigation, it is evident that the contribution to the

differential mode is related to alterations in the

vibration pattern known as

jitter and shimmer

classically (Titze, 1994).

Jitter is especially prone to

cause differences in the boundary between

neighbour cycles as can be inferred from the figures.

Therefore to grant a

jitter-independent analysis, ICA

should be applied to each possible combination of

phonation cycles in pairs after clipping and

interpolating each single phonation cycle, to match

cycle durations at the cost of assuming interpolation

side effects. This technique would open the

possibility of estimating the biomechanical

parameters in eq. (1) independently for each vocal

fold, thus opening important consequences for the

study of voice pathologies showing asymmetric

behaviour.

The application of ICA opens many other

interesting lines of study, as is for instance, the

spectral distribution associated to the differential

mode as compared to the common mode. It is well

known that the spectral distribution of the common

mode has much to see with the overall vocal fold

biomechanics (Gómez et al, 2009). The differential

mode, on its turn, may be strongly connected with

voice pathology correlates as Harmonics-to-Noise,

or Glottal-to-Noise ratios, which are known to be

good pathology indices. Another important study is

that of the statistical distribution of the differential

component, which is left also for a future

contribution.

5 CONCLUSIONS

Studies of the Glottal Source have concentrated

mostly up to now on the reconstruction of this signal

under conditions granting the most similarity as

possible to its physical counterpart (supraglottal

presure), which is not accessible in a simple and non

obtrusive way. The differences in duration and

amplitude of the glottal cycles which dominate the

pattern of the glottal source have been quantified by

distortion parameters as

jitter, shimmer or some of

their related siblings, but not much effort have been

inverted in quantifying and modelling these

differences. Up to a certain point it seems reasonable

to think that in short-term analysis these may be due

to asymmetries in vocal fold vibration. Knowing that

this is clearly a sign of non-normal phonation

(dysphonia), it would be greatly interesting to know

to which extent asymmetric vibration can be

understood and if this knowledge is amenable of

being applied to voice production and pathology

studies. The key to this methodology success is

granting good estimates of vocal fold vibration

asymmetry and this seems to be granted by the

application of Independent Component Analysis as

this preliminary study has brought to light. It may be

argued that other possible strategies to derive the

common and differential modes could have used, as

simple average. Needless to say that these naive

techniques do not grant the statistical independence

granted by ICA, therefore they cannot grant

independent estimates of each vocal fold

biomechanics, which is the key to the success of this

methodology. Going one step further, pathology

indices may be derived directly from the estimates

of the mixing matrix A, this being a preliminary

outstanding result. As the present study is limited in

its extension to explore the viability of the

methodology, many open questions remain in the

shelf to be answered in future studies. The objective

GLOTTAL SOURCE ASYMMETRY ESTIMATION BY ICA

563

by now seem to be accomplished according to the

results shown. The possibility of applying the

consequences derived from this work to voice

pathology and biometry studies are to be faced in the

near future.

ACKNOWLEDGEMENTS

This work has been funded by grants TIC2003-

08756, TEC2006-12887-C02-01/02 and TEC2009-

14123-C04-03 from Plan Nacional de I+D+i,

Ministry of Science and Technology, by grant

CCG06-UPM/TIC-0028 from CAM/UPM, and by

project HESPERIA (http.//www.proyecto-

hesperia.org) from the Programme CENIT, Centro

para el Desarrollo Tecnológico Industrial, Ministry

of Industry, Spain.

REFERENCES

Bäckström, T., Alku, P. and Vilkman, E., 2002. Time-

Domain Parameterization of the Closing Phase of

Glottal Airflow Waveform From Voices Over a Large

Intensity Range. IEEE Trans. on Speech and Audio

Proc. Vol. 10, pp. 186-192.

Berry, D. A., 2002. Examination of models of mucosal

wave propagation. J. Acoust. Soc. Am. Vol. 112, pp.

2446-2452.

Dworkin, J. P. and Meleca, R. J., 1997. Vocal Pathologies.

Singular Pub. Group.

Fant, G., 1960. Theory of Speech Production, Mouton,

The Hague, Netherlands.

Fant, G., et al., 2004. A four-parameter model of glottal

flow, STL-QSPR 4 (1985) 1-13. Reprinted in: Speech

Acoustics and Phonetics: Selected Writings, G. Fant,

Kluwer Academic Publishers, Dordrecht pp. 95-108.

Fast ICA: http://www.cis.hut.fi/projects/ica/fastica/

Gómez, P. et al., 2009. Glottal Source Biometrical

Signature for Voice Pathology Detection. Speech

Communication 51 pp. 759-781.

Hyvärinen, A., Karhunen, J., Oja, E., 2001. Independent

Component Analysis, John Wiley.

Plumpe, M. D., Quatieri, T. F., Reynolds, D. A., 1999.

“Modeling of the Glottal Flow Derivative Waveform

with Application to Speaker Identification”. IEEE

Trans. on Speech and Audio Proc., Vol. 7, No. 5, pp.

569-586.

Story, B. H. and Titze, I. R., 1995. Voice Simulation with

a Body-Cover Model of the Vocal Folds. J. Acoust.

Soc. Am., 97:2, pp. 1249–1260.

Titze, I., 1994. Principles of Voice Production. Prentice-

Hall, Englewood Cliffs, NJ.

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

564