REFLECTIONS ON NEUROCOMPUTATIONAL RELIABILISM

Marcello Guarini, Joshua Chauvin and Julie Gorman

Department of Philosophy, University of Windsor, 401 Sunset, Windsor, ON, Canada

Keywords: Knowledge, Neural Networks, Propositional Attitudes, Reliabilism, Representation, Representational

Success, State space models, Truth.

Abstract: Reliabilism is a philosophical theory of knowledge that has traditionally focused on propositional

knowledge. Paul Churchland has advocated for a reconceptualization of reliabilism to “liberate it” from

propositional attitudes (such as accepting that p, believing that p, knowing that p, and the like). In the

process, he (a) outlines an alternative for the notion of truth (which he calls “representational success”), (b)

offers a non-standard account of theory, and (c) invokes the preceding ideas to provide an account of

representation and knowledge that emphasizes our skill or capacity for navigating the world. Crucially, he

defines reliabilism (and knowledge) in terms of representational success. This paper discusses these ideas

and raises some concerns. Since Churchland takes a neurocomputational approach, we discuss our training

of neural networks to classify images of faces. We use this work to suggest that the kind of reliability at

work in some knowledge claims is not usefully understood in terms of the aforementioned notion of

representational success.

1 INTRODUCTION

Claims to propositional knowledge have the form, S

knows that p, where p is a proposition. Reliabilism is

a philosophical approach to the theory of

propositional knowledge. Among the necessary

conditions for some agent or subject S knowing

proposition p are that (a) p is true, (b) S believes p,

and (c) p is the outcome of a reliable process or

method. According to Alvin Goldman (1986, 1992,

1999, 2002) reliability is required for both epistemic

justification and knowledge. As we will concern

ourselves primarily with the reliability requirement

in this paper, we shall not engage the issue of what

might constitute sufficient conditions for either

knowledge or justification.

The reliability of a process or method is

understood in terms of a ratio: it is the number of

true beliefs produced by a process or method divided

by the total number of beliefs produced by a process

or method. A process that produces 100 beliefs, only

80 of which are true, is 80 percent reliable. We need

not concern ourselves here over exactly what the

standard of reliability needs to be either for

epistemic justification or for knowledge. What does

need to be noticed is that reliability, traditionally

understood, requires us to look at propositional

attitudes (either a belief that p, or acceptance that p,

or something along these lines) and truth.

It is not uncommon for philosophers to

distinguish between propositional knowledge on the

one hand and capacity knowledge or skill knowledge

on the other. Skill knowledge takes the form S

knows how to x, where x is some sort of behaviour

or action. While it is often contested whether it is

appropriate to say that pre-linguistic children or

animals have propositional knowledge, it is

generally conceded that they have various sorts of

capacity or skill knowledge. A dog may know how

to stay afloat and swim in water without any

propositional knowledge of the physics of these

matters.

Paul Churchland’s “What Happens to

Reliabilism When It Is Liberated from the

Propositional Attitudes?” (chapter six of

Neurophilosophy at Work) is a thought provoking

attempt to take a reliabilist approach to

epistemology, divorce it from propositional

attitudes, and explain how we can have non-

propositional knowledge. Churchland begins by

enumerating many instances of know-how. The

examples include the knowledge possessed both by

humans and non-humans. He argues that much of

what we call knowledge has little or nothing to do

with the fixing of propositional attitudes. There are

many useful and important insights here. He also

711

Guarini M., Chauvin J. and Gorman J..

REFLECTIONS ON NEUROCOMPUTATIONAL RELIABILISM.

DOI: 10.5220/0003293307110716

In Proceedings of the 3rd International Conference on Agents and Artiﬁcial Intelligence (ICAART-2011), pages 711-716

ISBN: 978-989-8425-40-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

goes on to argue that a reliabilist epistemology can

be developed that requires neither propositional

attitudes (belief or acceptance) nor truth. This is a

striking claim. After all, the reliabilist understands

knowledge in terms of reliably arrived at true

beliefs. Clearly, this way of doing things requires

talking about both propositional attitudes and truth.

Churchland tries to formulate a reliabilism where

neither truth nor propositional attitudes are required.

In the process, he develops a notion of

representational success and defines reliability in

terms of it. We will argue that at least in some cases

of attributing skill knowledge or know-how, the

notion of representational success is simply not

needed. At best, representational success might play

a role in explaining the source of reliability, but even

that will be shown to be less attractive than it first

appears.

2 RELIABILITY AND

REPRESENTATIONAL SUCCESS

Churchland recognizes the importance of truth in

classical approaches to reliabilism, but he resists

talking of truth since (a) it attaches to propositional

attitudes, and (b) much of our knowledge is not

about fixing propositional attitudes. In place of truth,

Churchland formulates a notion of representational

success that is compatible with analyses of neural

networks. To keep things simple, consider a three

layer feed forward neural network. When it is

trained, it will have a hidden unit activation vector

state space that is multiply partitioned. Each

different pattern of activation across the hidden units

is a different point in that space. We can then

measure the distance between points (which

Churchland often refers to as similarity relations). In

short, this space in question is a kind of similarity

space. Churchland treats (somewhat metaphorically)

similarity spaces as maps that guide our interactions

with the world. Just as a map is representationally

successful when the distance relations in the map

preserve distance relations in the world, conceptual

spaces understood as similarity spaces are

representationally successful when they preserve

various similarity or distance relations in the world.

In the ideal case, representational success would

occur when the relative distance relations between

the learned points in state space correspond to real-

world similarity relations. Since the preservation of

similarity relations requires many points in space

and many relations between them, some kind of

holism is entailed by this position. It cannot be the

case that one representation (or individual vector),

all on its own or in the absence of other

representations (or vectors), can be

representationally successful. Since representational

success is cached in terms of preserving similarity

relations between vectors/representations,

representational success is a notion that attaches to

multiple representations all at once.

On classical accounts of reliabilism, the

reliability required for knowledge is a function of

true beliefs. Churchland’s representational success,

loosely modeled after the representational success of

maps, is his replacement for truth. Churchland

(2007, p. 111) understands conceptual spaces as

similarity spaces, and the reliability requirement for

knowledge amounts to the claim that a conceptual

framework or similarity space be “produced by a

mechanism of vector-fixation that is generally

reliable in producing activation vectors that are

[representationally] successful in the sense just

outlined.”

We just tended to the issue of how Churchland

formulates reliabilism without reference to truth.

Before going further, we need to review how he

conceives of theories. Churchland treats the

information stored in the synaptic weights of a

network as the network’s theory. His criterion for

theory identity has to do with the distance relations

that hold between points in hidden unit activation

vector state space. He wants to allow for the

possibility that different sets of synaptic weights

may implement the same theory. Given two sets of

synaptic weights, S1 and S2, they can be said to

implement the same theory if they lead to a

partitioning of hidden unit activation vector state

space such that the distance relations between

points, in the respective state space they generate,

are preserved. In this way, we can understand what it

means for a theory to change or stay the same in one

network, and what it means for two different

networks to implement the same or different

theories.

What if we had a non-propositional task

performed by a network where (a) we could measure

reliability and (b) that reliability was not understood

in terms of the aforementioned notion of

representational success? This would be a problem

for the type of position Churchland has developed.

In the next section we describe some neural

networks so that in the fourth section, we can

discuss scenarios where representational success is

not needed to discuss reliability.

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

712

3 SEX CLASSIFICATION

NETWORK

In this section, we will describe artificial neural

networks (ANNs) that we have trained to classify

images of faces as either male or female. All of the

networks created were three-layer, fully

interconnected feed-forward networks trained by

supervised learning using the generalized delta rule.

To conduct our experiments, images were first

converted into vectors that were capable of being

analyzed by the ANN. The converted vectors

consisted of 5824 dimensions, one for each pixel of

the image, where each image was 64 x 91 pixels.

Each unit (i.e., each pixel) varied from 0 to 255,

which corresponds to the 256 shades of grey in the

images. All networks discussed contained 1 output

unit, 60 hidden units, and 5824 input units. We

experimented using both sigmoid and radial basis

activation functions. Although the results were

comparable, we opted to carry out most of our trials

using sigmoid activation functions. The results in

this paper reflect this preference.

Initially there were 101 images. However, due to

image/file corruption, a number of the images were

either corrupted outright or corrupted during the

vector conversion process. A total of 89 images were

used for training and testing purposes.

For training purposes, the desired output for all

female images was set to 0; the desired output for all

male images was set to 1. For testing, any output

result over 0.5 was interpreted as a male

classification, and any result below 0.5 was

interpreted as a female classification.

The training and testing runs we will discuss

herein are of two types. First, we trained on partial

sets. We randomly selected 44 images, used them

for training, and then we tested on the remaining 45.

We also trained on the 45 image set, and tested on

the remaining 44. Second, we trained the network on

the entire 89 image corpus.

4 A DISCUSSION OF

CHURCHLAND’S POSITION

The first point we want to make is that, given the

way Churchland defines theories and

representational success, it is possible for two

different theories to have equal levels of

representational success. Consider, for example,

networks N1 and N2. N1 was trained on 44 images

and tested on 45; N2 was trained on 45 images and

tested on 44. Each had its weights randomly

selected; each was trained using the same parameter

values, and each achieved essentially the same level

of success in classifying outputs of previously

unseen images (approximately 89%), but there are

important differences in the cluster plots. These

plots pair each face with its closest neighbour in

state space; then averages for each pair are

computed, and each average is paired with its closest

neighbour, and so on. Figure 1 is the cluster plot for

N1, and Figure 2 is the cluster plot for N2. While

there is some overlap between the plots, there are

important differences as well. An examination of the

lower portions of the cluster plots immediately

reveals some significant differences. We have two

networks with equal levels of classificatory success,

but each implements a different theory. This does

not change if we train the network on the entire set

of images. If we randomly select weights for

networks N3 and N4, and train each on the entire

training corpus with perfect classificatory success,

we can still generate different cluster plots (or

theories) for the networks. Assuming this means that

we can say that N1 and N2 have equal levels of

representational success, and N3 and N4 have equal

levels of representational success, then there is a

difference between classical truth as correspondence

and Churchland’s substitute, representational

success. On classical conceptions of theories and

truth, two inconsistent theories cannot both be true.

However, it may well be that two conflicting

theories (in Churchland’s sense of “theory”) can

both be equally representationally successful. There

may well be different ways of measuring similarities

and differences between faces, and different

networks may hone in on different features or

relations, or perhaps on the same features and

relations but weigh them differently, leading to

different similarity spaces (or different theories) that

achieve equally good or even perfect performance.

We offer this as a point of clarification since it might

be something Churchland (2007, p. 132-134) is

happy to concede.

The second point we want to make is that

representational success and reliability appear to

come apart. Remember, Churchland defines

reliability in terms of representational success. With

networks N1 and N2, we achieved 89%

classificatory success on new cases, and with N3 and

N4, we achieved 100% classificatory success on the

total set of images. Notice, we said “success,” not

“reliability.” To talk of reliability in Churchland’s

sense, we would have to be assured that the distance

relations in the state spaces map on to distance

relations in the world, since reliability is defined in

terms of representational success. However, it seems

REFLECTIONS ON NEUROCOMPUTATIONAL RELIABILISM

713

Figure 1: A cluster plot of faces for network N1’s state space. M = male; F = female.

perfectly natural in cases like these to talk about the

reliability of the network even if we have no prior

views on the level of representational success

achieved. To see this, let us consider two scenarios.

First, consider two hypothetical networks, N5 and

N6, and let us say that training leads to poor

classificatory performance. Second, consider

hypothetical networks N7 and N8, and let us say that

training leads to outstanding classificatory

performance. Our intuition is that it is quite

reasonable to say that N5 and N6 have poor

reliability and that N7 and N8 have high levels of

reliability before we learn anything about the

structure of the hidden unit activation vector state

spaces of any of these networks. Before doing any

sort of detailed analysis, we simply do not know

exactly which distance relations in faces the

networks are honing in on during training, and for

purposes of discussing reliability, it just does not

seem to matter. But Churchland’s definition of

reliability in situations like this is about the level of

success with respect to distance relations in state

space mapping on to distance relations in the faces

(i.e., real-world features). If an objector were to

insist that this is not a problem since, in spite of our

not being aware of it, networks having high levels of

classificatory success are constructing similarity

spaces that map on to the world, and those without

classificatory success are not producing such spaces,

then it is not clear how much explanatory work the

notion of representational success is doing for the

notion of reliability. In arguing against a pragmatist

notion of truth, Churchland (2007, p. 103) claims

that he would not want to explain truth in terms of

successful behaviour, and representational success is

his substitute for truth. We are suggesting that the

only evidence we have for success in the networks

we have been considering is successful classificatory

behaviour. (We are not arguing for a pragmatist

theory of truth. Rather, we are suggesting that when

it comes to explaining know-how or attributions of

know-how, a system’s or individual’s behaviour is

very much of the essence.) Whatever the structure of

state spaces generated by N5 and N6 (whether they

are the same or different) we will say that they are

unreliable. Whatever the structure of the state spaces

generated by N7 and N8 (whether the same or

different) we will say that they are reliable. And we

will make our claims based on behaviour. What we

are interested in when discussing a network’s (or an

individual’s) reliability in classifying faces is the

ability to successfully perform. One further piece of

evidence for this is that when we make attributions

of know-how, we are not much interested in how

that know-how is achieved. For example, if we say

that two year old Jasmine knows how to recognize

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

714

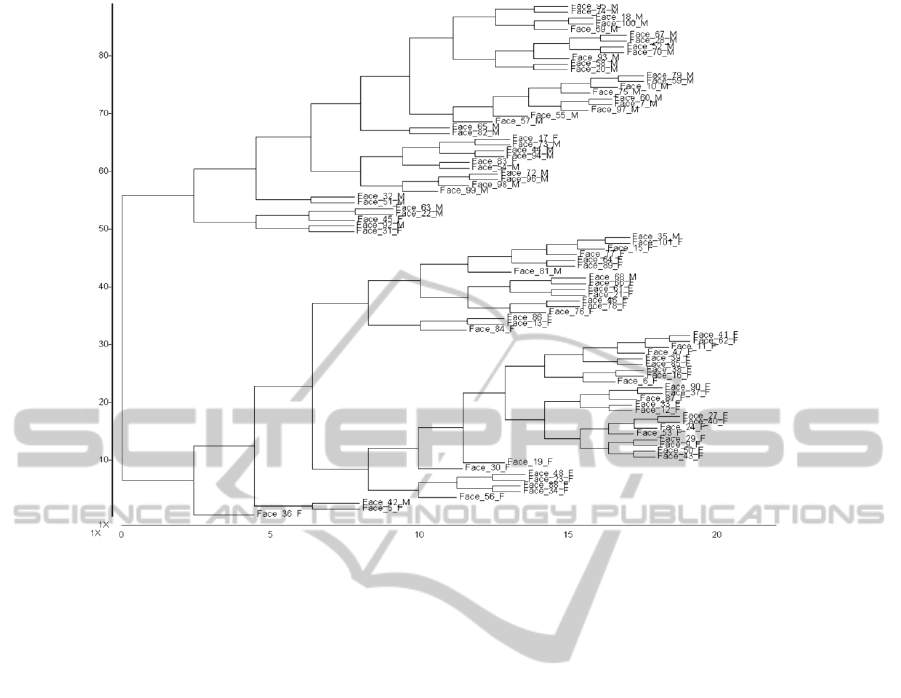
Figure 2: A cluster plot of faces for network N2’s state space.

boys and girls by looking at their faces, we are

saying that Jasmine can perform this task very well,

and that we can rely on her to do so. Robert

Brandom (2000, chapter 3) discusses the importance

of the intersubjective nature of knowledge

attribution (though his focus is on propositional

knowledge, whereas ours is on capacity or skill

knowledge). We can say all of this without ever

knowing the structure of her face state space and the

ways in which its distance relations do or do not

map on to the world.

The above arguments assume that equal levels of

classificatory performance mean equal levels of

representational success. Some might challenge this

assumption, but we do not think that doing so leads

to a plausible defence of Churchland’s position.

Consider: if two networks can achieve perfect

classificatory success, and that is still not enough to

say that they are equally representationally

successful, then the notion of representational

success seems puzzlingly irrelevant to defining

reliability since in such cases, surely we would like

to say that the networks in question are equally

reliable; that is, that they know equally well how to

classify faces as male and female.

It might be thought that a neurocomputational

reliabilist would remain content with saying that

representational success explains successful

behaviour, and if there is more than one way to be

representationally successful, then it will turn out

that there is more than one way to explain how the

successful behaviour was arrived at. Perhaps, in the

end, such a response may be made to work, but

much work would have to be done. There are many

logically possible metrics. See Laakos and Cottrell

(2006) for an extended discussion of the importance

of metrics. Churchland appears to assume that the

distances between points in state space are Euclidean

distances. Mahalanobis distance, city block or taxi

cab distance, and other metrics are available. For the

sake of argument, say that by using a Euclidean

metric, a given set of faces is very similar in the

state space for network N9, and by using a

Mahalanobis metric, they are not similar. Is N9

representationally successful or not? Is N9 reliable

or not? We suspect that you probably want to know

how N9 performs in terms of classifying faces

before you answer these questions. When

Churchland remarks that street maps are

representationally successful in virtue of preserving

distance relations in the world, it must be understood

that there is a preferred metric for distance at work.

We have been considering a case (faces in state

space) where it is not obvious that there is a

preferred metric. Without a preferred metric, it is not

clear what talk of preserving similarity relations

amounts to (since such talk is a function of some

metric). In the absence of a preferred metric for

REFLECTIONS ON NEUROCOMPUTATIONAL RELIABILISM

715

similarity relations, performance becomes the

driving consideration since it is not even clear what

representational success (in Churchland’s sense)

amounts to if we do not have a preferred metric.

However, we can still have capacity knowledge in

such cases (for example, the male-female

discrimination task).

4.1 Of Maps and State Spaces

Finally, let us close with some reflections on the

map metaphor, which appears to inspire many of

Churchland’s thoughts on these matters. The idea is

that a street map is representationally successful

because it preserves distance relations that are in the

world. Part of what makes this metaphor attractive is

that such a map would cease to be a reliable guide if

it did not at least roughly track distance relations in

the world. Imagine that the map says your desired

exit is 10km away and, in fact, it is only 0.1km away

– that is an exit you will likely miss. In a case like

this, tracking a specific set of distance/similarity

relations in the world is the key to success.

However, the point does not generalize to all state

spaces set up by neural networks being seen as high

dimensional maps that preserve distance/similarity

relations in the world. The burden of the discussion

section has been to show that we can have high

levels of success (in face classification) with

differing similarity or distance relations. When that

happens, we can still talk of how reliably a system

performs some task, but the notion of

representational success (as Churchland defines it)

does not play a role in defining that reliability.

In the case of the street map, there really is a

kind of plausibility in saying that what explains the

reliability of the map is that it preserves certain

distance relations in the world. Two points need to

be made about this. First, we need to understand that

there is a difference between these two things: (a)

being reliable and (b) explaining the source of that

reliability. We have seen that we can understand

what it is for a system (a face classifying neural

network) to be reliable independent of understanding

the source of that reliability. Churchland uses the

notion of representational success (or preservation of

distance relations) both to define reliability and to

understand its source (i.e. to do both (a) and (b)). As

we have seen, we can say that a system is reliable

without having any information about the

preservation of distance relations. Second, we need

to be careful not to overstate the explanatory work

the preservation of a set of distance relations does

when there are many possible sets of such relations.

If S1, S2, … Sn are all different sets of similarity

relations that lead to equal levels of reliability in

classifying faces, then it cannot be said that the

network is successful because it persevered the

similarity or distance relations in the world. The

most that can be said in explaining the source of

reliability is that the network is reliable because it

captured or preserved one of S1 through Sn. We do

not want to suggest that such a claim would be

vacuous. It is not. However, it is not nearly as

powerful or attractive as the case where there

appears to be a single set of similarity relations in

virtue of which reliability is achieved. The street

map metaphor is suggestive of such a powerful case;

there is no reason to expect that sort of case to

capture what is going on in all cases of classificatory

reliability in neural networks.

The street map example may be a special case. It

turns out to be (optimally) reliable or something we

can rely on if, and only if, a specific set of distance

relations from the world are preserved by the map.

We have not been given a reason for thinking that

such will generally be the case when the high

dimensional similarity spaces set up by neural

networks are compared to the world. Churchland’s

position is at its strongest when dealing with cases

like the street map. We take ourselves to have shown

that such an example does not always generalize.

The extent to which it might generalize is a question

for future work.

ACKNOWLEDGEMENTS

We thank the Shared Hierarchical Academic

Research Computing Network (SHARCNet) for

financial support.

REFERENCES

Brandom, R. (2000). Articulating Reasons. Cambridge,

MA: Harvard University Press.

Churchland, P. M. (2007). Neurophilosophy at Work.

Cambridge, UK: Cambridge University Press.

Goldman, A. (1986). Epistemology and Cognition.

Cambridge, MA: Harvard University Press.

Goldman, A. (1999). Knowledge in a Social World. Oxford:

Oxford University Press.

Goldman, A. (1992). Liaisons: Philosophy Meets the

Cognitive and Social Sciences. Cambridge, MA: MIT

Press.

Goldman, A. (2002). Pathways to Knowledge, Private and

Public. Oxford: Oxford University Press.

Laakso, A. and Cottrell, G. (2006). Churchland on

Connectionism. In Keeley, B.L. (Ed), Paul Churchland.

Cambridge, UK: Cambridge University Press.

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

716