OVERHEARING IN FINANCIAL MARKETS

A Multi-agent Approach

Hedjazi Badiâa

Information Systems Division, CERIST Research Center on Scientific and Technical Information

Ben Aknoun, Algiers, Algeria

Aknine Samir

GAMA Laboratory, Lyon 1 University, Lyon, France

Ahmed-Nacer Mohamed

Information Systems Laboratory, USTHB University of Science and Technology Houari Boumediene, Algiers, Algeria

Benatchba Karima

ESI, National High School of Computer Science, Algiers, Algeria

Keywords: Multi-agent system, Financial market, Simulation, Overhearing, Speculation, Classifier system.

Abstract: Open complex systems as financial markets evolve in a highly dynamic and uncertain environment. They

are often subject to significant fluctuations due to unanticipated behaviours and information. Modelling and

simulating these systems by means of agent systems, i.e., through artificial markets is a valuable approach.

In this article, we present our model of asynchronous artificial market consisting of a set of adaptive and

heterogeneous agents in interaction. These agents represent the various market participants (investors and

institutions). Investor Agents have advanced mental models for ordinary investors which do not relay on

fundamental or technical analysis methods. On one hand, these models are based on the risk tolerance and

on the other hand on the information gathered by the agents. This information results from overhearing

influential investors in the market or the order books. We model the system through investor agents using

learning classifier systems as reasoning models. As a result, our artificial market allows the study of

overhearing impacts on the market. We also present the experimental evaluation results of our model.

1 INTRODUCTION

In finance, many researchers have developed models

that capture the dynamics observed in actual

markets. The models proposed for over a hundred

years ago are, mostly "group-based". A group-based

model (Derveeuw, 2008) describes the mass laws in

a population by making very simplistic assumptions

based for example on an average behaviour. For

instance, modern portfolio theory (Markowitz, 1952)

is based on the assumption that all investors are

similar in their attitude to risk. Thus conventional

finance studies trader populations whose aggregated

behaviour is described by globalizing mathematical

equations systems. But this theory does not

reproduce stock prices data series properties.

Because of these limitations, some researchers have

turned to individual-based models (Derveeuw,

2008). These latter models put system actors at the

heart of the model. Each part is modelled

individually together with its relationships with

other entities. Multi-agent systems (MAS) are part

of individual-based modelling. In these models,

agent behaviour is a consequence of its observations,

knowledge and interactions with other agents. The

individual-based approach fully meets requirements

imposed by complex systems studies as financial

markets. Multi-agent modelling and simulation of

342

Badiâa H., Samir A., Mohamed A. and Karima B..

OVERHEARING IN FINANCIAL MARKETS - A Multi-agent Approach.

DOI: 10.5220/0003293603420350

In Proceedings of the 3rd International Conference on Agents and Artiﬁcial Intelligence (ICAART-2011), pages 342-350

ISBN: 978-989-8425-41-6

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

markets can seize the complexity without reducing

it. Despite the existence of multi-agent financial

markets models as the SF-ASM (LeBaron, 1999)

and the extended Genoa Artificial Stock Market

(Cincotti, 2006), informal interactions between

investor agents have been neglected, hence our focus

on overhearing concept to address these problems.

In MAS, the communication is generally

organized in protocols determining the order of

exchanged messages. This limits the impact of

communication, and in a highly interactional, as

financial markets, this is insufficient since the

interactions are not only based on pre-established

protocols, but also on the need that each agent has to

interact in its environment. In (Dugdale, 2000)

where the objective is to simulate the interactions in

an emergency call center, it is shown that

overhearing (Balbo, 2004) is an important factor for

the effectiveness of the company agents (operators)

as it directly affects their behaviour. Overhearing

corresponds to the fact that an agent has a tendency

to intercept messages that are not clearly directed to

it. What is important is that the sender knows that

this will happen. The overhearers keep within legal

status, i.e. it is part of the operating system (Legras,

2003). In this paper we propose a financial market

multi-agent model and introduce the overhearing

concept to test its impact on it. To model the agent

we use a learning classifier model. In our work, the

classifiers allow on one side the representation of

complex behaviours of agents based on rules and on

the other side the modelling of key features that

must have an investor agent which are evolution and

adaptation to dynamic environment. This article is

organized as follows. In Section 2 we introduce

artificial financial markets. In section 3 we discuss

the main existing works and their limitations.

Section 4 is devoted to our model and Section 5 to

the presentation of simulation results.

2 ARTIFICIAL STOCK

MARKETS

While financial markets are organized in different

ways, three major components emerge (Figure 1):

1. Market structure: market is structured around a

set of rules describing and governing its trading

details as the process of price computation. This set

of rules is called market microstructure.

2. Economic agents: who invest their capitals.

Around these investors, other agents exist such as

brokers which may be in the market or outside.

3. Information: Investor agents make decisions

using the information from the external world,

information from the endogenous market itself and

information from their peers.

Figure 1: Market model structure.

Price fixing and market microstructure is the

heart of an artificial market. Two types of

microstructures exist: synchronous models need to

receive the wishes of the agents before producing a

price and asynchronous models that do not have

time constraints. Investor agents are the most

important components of the market, they

continually seek their interests. To build their

investment strategies they begin by assessing stocks

by technical, fundamental or quantitative analyses.

Fundamental analysis is based not on the prices

but on the economic reality of the business. The

future asset price is based on market shares,

revenues, etc.

Technical analysis provides market future trend

by observation of past prices graphically or

statistically.

Quantitative analysis focuses on risk of a

financial asset. Whatever its origin (economic,

financial), risk is reflected in fluctuation of the

financial value of an asset. It is the same as the price

volatility of the asset which is measured through the

standard deviation of past prices. It is then

interpreted as a measure of the dispersion around the

average price. According to (Streichert, 2006),

volatility is calculated as follows:

(

)

(x)



(1)

Where (X) =



V(X) With: 

(



)

∑

(







)









and

̅ =

∑











. Xi is the asset X price at time i.

The more the volatility is high, the more the risk is

high. This means that its price fluctuates abruptly

from the highest to lowest.

3 RELATED WORK

The Santa Fe Artificial Stock Market (SF-ASM)

(LeBaron, 1999) is the first agent-based artificial

Microstructure

External

world

Agents

Informations

Desires

Informations

OVERHEARING IN FINANCIAL MARKETS - A Multi-agent Approach

343

financial market. This model is based on the

synchronization of decisions. From an equation that

centralizes agent decisions through the opposition of

supply and demand, new asset price is calculated.

Then comes the clearing phase to make transactions

between buyers and sellers agents. It is clear that this

model does not reflect the transactions in a real

market where each agent is free to express its desires

freely. Other models such as the Genoa Artificial

Stock Market (Cincotti, 2006), $-game (Andersen,

2003) or Toy Model (Bak, 1996) are synchronous in

their majority, or even in the few attempts to

asynchronous markets such as Toy model they lack

realism considerably. For example, in the Toy

Model agents can hold at most one asset. They are

therefore not free to sell or buy the quantities they

want to trade. This model is toy in the sense that no

real market works in that way. The synchronous

model is representative of the financial markets with

market makers and cannot be extended to an order-

driven market where transactions are done

asynchronously and where the price follows the

dynamics of market participants. The manner in

which agents state their wishes in these models is

not realistic. In most models (Derveeuw, 2008),

agents make their desires in the form of a simple

direction (buy or sell), while in reality they are

expressed with a triplet (direction, price, quantity).

Note also the existence of works in financial markets

modelling such as in (Streichert, 2006), which

focused on the study of time series of financial

indices using the classifier Systems, but the limit is

found in the neglect of the formal or informal

interactions between agents in the market. Another

aspect not approached in these works is the study of

agents reasoning modes and therefore their

behaviour evolution. In our model, we seek to

emulate as closely as possible the economic reality.

We use a multi-asset model. Each order is thus

expanded to a quartet (asset, direction, price,

quantity). The behaviours of our investor agents are

complex and heterogeneous to be able to analyze

and interpret the results of their behaviour. Within

the same market, we model agents tolerant or risk

averse, leader and follower agents. These last two

types of agents are based on the overhearing

mechanism.

Leader agent tries to manipulate the market

taking advantage of the naivety of the other agents

(followers) supposed less informed than him to

make profits from future price fluctuations. Leader

agent has the advantage of receiving informational

signals before the others.

4 MULTI-AGENT MARKET

MODEL

Our artificial financial market model (Figure 2) has

three main components, namely: the microstructure

of the market, agents which compose it and the

external world. Our model is governed by

asynchronous orders. It allows agents to make their

decisions and actions autonomously. This

configuration is representative of the largest

financial markets like NYSE or Euronext. Modelling

with order book is more complex than a

synchronous market (as with Market Maker). For

each asset are associated two order books (buy, sell),

each containing the five best orders. The agents of

the system are the market itself which manages real-

time transactions and thousands of investors. An

investor chooses shares to buy or sell, contacts the

market and manages its financial portfolio. An

investor may use the services of an Overhearing

Agent which will get some information from other

investor agents by using overhearing concept.

Figure 2: General representation of the system.

1. A Market Agent (MA): represents the financial

market and has five tasks: (1) Receive orders issued

by investor agents; (2) Sort orders by their types,

directions and arrival times; (3) Asset pricing; (4)

Communicate order books to investors; (5) Check

the satisfiability of orders, conduct transactions and

ensure payment.

When the Market Agent finds two orders of

opposite directions that are counterpart, it makes the

transaction after confirmation from both parties.

Therefore, the market agent saves the transaction

and updates the concerned orders then informs the

two investor agents that the transaction was made.

2. Overhearing Agents (OA): provide information

not displayed on order book to investor agents

having request it. They perform the following tasks:

(1) Follow buying and selling orders of the investors

Market

BDD

Investors

Learning

classifier

system

Parametrization

Orders

Market

informations

Simulation

results

Information

rocessin

Market institution

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

344

that it is responsible to overhear; (2) Sort

information gathered for each asset and

communicate it to investors asking overhearing.

Overhearing Agent represent the concept of

overhearing in our system. These agents will "hear",

which means intercept messages from an agent or a

group of Investor agents when they receive the

request from one or more agents. The main function

of Overhearing Agent is to sort the information it

has collected and distribute to requesters (Figure 3).

Figure 3: Overhearing Agent internal architecture.

Overhearing Agent shall first make a

classification of agents according to their portfolio

amounts. The first agents in the ranking will be

overheard. Overhearing Agent intercepts all

transaction confirmation messages issued by these

agents and sends the results to the requester (Figure

4).

Figure 4: Overhearing process stages.

Investor Agents are constantly interacting with the

Market Agent by sending orders and with the

Overhearing Agents through their possible requests

for overhearing.

3. Investor Agents (AI): influence stock prices. An

Investor Agent performs the following tasks: (1)

Issues an order on an asset; (2) Consults order books

to be informed by the other agents desires; (3) Con-

sults and manages financial portfolios; (4) Uses

Overhearing Agent services; (5) Makes payment if

the agent is buyer or increases its liquidity if seller.

We distinguish two types of Investor Agents:

IAE asking the services of an Overhearing Agent

and IA without access to this service. To achieve its

goals, Investor Agent may make a request to

overhear to an Overhearing Agent. The latter will

then overhear other Investor Agents and gather

information concerning their transactions and the

amount of their portfolios. It also classifies the

overheard agents by the amount of their portfolios

and then informs the Investor Agent. An Investor

Agent's primary goal is to be always satisfied or win

whatever the transaction. To achieve this, it will be

equipped with a reasoning module allowing it to

adapt to its environment and to learn from past

experiences (bounded rationality) (Kotzé, 2005).

Learning Classifier systems (Arthur, 1994) are the

support we used to model such agents (Figure 5).

Investor Agents IA use order books available assets

on the market to make decisions while the IA

driven by information obtained by Overhearing

Agents. These agents intercept messages of

overheard Agents and transmit them analyzed to

Investor Agents.

Figure 5: Internal architecture of the Investor Agent.

To approach the reality, we introduce two pairs

of behaviours to the two categories of Investor

agents:

1. (Risk Tolerance, Risk Aversion): an Investor

Agent may be either risk-averse or risk-tolerant. In

the first case, Investor Agent wishes always to be

sure that the transaction is with no risk. The risk

tolerance TR, is then equal to 0 throughout the

simulation.

In the second case, the agent will have a certain

percentage of risk tolerance, the variable TR is equal

Communication

Detector:

Perceptions

Treatment and

sorting information

Overhearing

module

External world

Effector:

Sending

informations

Service requesters

ents

Overhearing

Overheared

ents

External world

Detecto

Decision

Action

Other A

ents

Communication

Rules: - R

- .

-R

Learning: Bucke

Brigade Algorithm

Covering: Genetic

algorithm

Investor

Classifier system

Parameterize overhearing

Investors overhearing

Overhearing

Send information

AMS (JADE)

uest

(

sniff-a

ent-on

(

liste-

Inform

Setup ()

Search and sort

of the biggest

investors.

Request

(Overhearing)

Inform

(Overhearing)

OVERHEARING IN FINANCIAL MARKETS - A Multi-agent Approach

345

for example to 20%, and this means that the agent

will choose an asset with risk which may not exceed

20%. For risk-tolerant Investor Agents, the TR

variable is not fixed; it will be updated according to

their portfolios changes.

2. (Leader, Follower): other behaviours that we

consider are follower or leader feature of an agent.

An Investor Agent Leader will not be influenced by

the actions of other Investor agents, therefore it will

not use the services of an Overhearing Agent. If

Follower, its decisions will be governed by the

actions of other Investor agents; it is this class of

agents who use the services of an Overhearing

Agent. This behaviour enables Investor Agents to

make decisions in the form of the following

quadruplet: (asset, direction, price, quantity). Let's

see how the quad is generated.

5 INVESTOR AGENT

REASONING

We note the choice of asset and direction (buy or

sell) is the first step in decision making for an

Investor Agent. This selection is done through the

classifier system of each class of agent (IA

and IA).

The price is calculated by agent according to its

nature and tolerance or aversion to risk (Table 1).

Table 1: Summary of the pricing policy.

F/L IA

/IA A/T Pricing policy

0 0 0 Agent follows overheard agent price.

0 0 1 Agent follows the price of the

overheard agent and adds the

percentage of risk tolerance.

0 1 0 Agent takes the first price in the

order book which ensures the

transaction (a counterpart).

0 1 1 Agent randomly chooses a price in

the order book

1 1 0 Agent randomly chooses a price in

order book and adds or subtracts it

2%.

1 1 1 Agent randomly chooses a price in

the order book and adds or subtracts

it 5%.

F: Follower agent (0); A: Risk-averse (0);

L: Leader agent (1); T: Risk-tolerant (1);

: Investor Agent using overhearing agent services (0);

IA: Investor Agent not using overhearing agent services (1);

The quantity is the last variable to be determined

in order to complete the quadruplet and issue an

order to the market agent. The quantity is calculated

as follows: when the Investor Agent defines its asset

price, it calculates the number of shares they can buy

or sell by dividing its cash on price. The quantity is

for example a percentage of 5% of the result.

Although they come together on how to interact

with the market agent, the IAE and AI agents have

two different reasoning modes through their two

classifier systems CS1 and CS2 respectively.

Classifier systems allow for incrementally learn

the rules that define the behaviours of the agent. To

model these agents we have used the Michigan

classifier system (Buche, 2006) perfectly suited to

our problem since our Investor Agents must learn

quickly and adapt instantly to changing situations

over time. The rules of a classifier system are

renewed by a genetic algorithm and reinforced by

the Bucket Brigade Algorithm (Holland, 1982).

We present for each category of Investor Agent

(the IA and IA

) its learning module. We model two

classifier systems, one for each type of Investor

Agent. In our model, we assume that we have:

1. A number N of assets available on the market;

2. A number M of Investor Agents in the

simulation. Agent behaviour will be of two types:

leaders or followers in addition to their degree of

risk aversion;

3. Buying and selling trends of the N assets is

analyzed from order Book information.

4. At the beginning of each simulation, the user

chooses the number of Investor Agents the

Overhearing Agent will overhear; this number is set

throughout a simulation. S is the number of

overheard Investor Agents, 1 ≤ S ≤ M-1.

5. To study the overhearing impact on Investor

Agents and the market, Investor agents will be split

into two groups; Those agents which will use the

service of an Overhearing Agent and Agents which

do not use this service.

5.1 Classifier System 1 (CS1)

CS1 defines asset to choose and its direction (buy,

sell). CS1 corresponds to IA agents’ category.

Condition Part: composed of N bits. The first bit

corresponds to the first asset and the Nth bit

corresponds to the Nth asset. The presence of 1 in a

bit of position i means that the asset i is in buy

tendency else sell tendency. When trend for buying

an asset is equal to selling; this bit is set to 1,

favoring purchase to sale.

Action Part: is composed of log

N + 2 bits. It

indicates the asset and its direction. For a number N

of assets, we need log

N bits to represent the asset

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

346

number; we use for that the log

N first bits. The

next bit determines if the Investor Agent will issue

an order for the asset chosen or not. It is the bit of

action/inaction. If it is 0 then the Investor Agent

shall make no action concerning the chosen asset, if

1 then it will initiate action represented by the last

bit; if the latter is 1 then the Investor Agent issues a

buy order otherwise a sell order.

Reward and Selection of Best Rules: Rules are

remunerated primarily depending on the type of the

Investor Agent (Follower or Leader); a rule which

has the purchase of an asset when there is a tendency

for sale for an Investor Agent Follower, will

obviously be poorly remunerated. The rules

containing logical errors, such as the presence of two

1 in the last two bits of the action part will be

automatically rejected. The reward is updated

continuously according to the degree of agent risk

aversion. For each rule the risk for the selected asset

may be calculated in order to reward the rule. Note

that the reward is a real number between 0 and 1. To

calculate the asset risk we first compute the variance

the last 10 days prices then standard deviation and

finally we measure volatility corresponding to asset

risk using dispersion coefficient with equation (1).

The dispersion coefficient represents the risk of the

asset is a percentage included in the interval [0, 1].

The more it approaches 1 the more a stock is risky

and vice versa. Finally, calculation of the reward

will be different depending on whether the investor

agent is risk-averse or tolerate a certain percentage

of risk. For risk averse investor agents the reward is

calculated as in equation (2):

Reward = 1 – Risk (2)

More the asset risk increases more the reward of the

rule decreases. For agents tolerant to a certain risk

percentage (TR), the reward is equal to (3):

Reward = 1 – (TR – Risk) (3)

More the asset risk approximates to the risk

tolerance TR of an agent, more the reward of the

rule is well remunerated and vice versa. Note that if

the risk exceeds the tolerance for risk, the reward of

the rule will be equal to 0. For risk-tolerant agents,

TR changes value depending on whether they win or

lose money. More an agent earns, more is more its

risk-tolerant, more TR increases and vice versa.

5.2 Classifier System 2 (CS2)

CS2 defines (for IA

Followers) which Investor

Agent to follow. After selecting the Investor Agent

to follow, classifier system chose asset and action to

perform. Followed Investor Agent is IA

or IA.

Condition Part: It is composed of

log

S + log

N +

1 bits. The first part of the condition represents the

number of overheard Investor Agents. It concerns

the

log

S first bits. The second part of the condition

represents the number of assets purchased or sold by

the overheard Investor Agent, we must have

log

bits for representing all assets. The last condition bit

represents the action made by the overheard agent

on the given asset. If this bit is equal to 1 then

Investor Agent bought this asset else it sold it.

Action Part: composed of one bit, if this bit is 1then

the IA

follow of the overheard agent else no.

Reward and Selection of Best Rules: The rules

remuneration is done using three criteria:

1. Weight of each overheard agent is calculated

from the amount of its portfolio, i.e., amount of its

liquidity plus average values of its assets (Table 2).

Table 2: Investor agents weights to overhear (example).

N° Investor Agent Portefolio amount Weight

06 50.000

0.5

20 30.000

0.3

11 20.000

0.2

2. The risk in the purchase or sale of the chosen

asset which is calculated on the price volatility

during 10 days (like for SC1).

3. The risk aversion of the IA

For CS2 rules remuneration, Overhearing Agent

performs a ranking of the S overheard agents and

calculates the weight of each one (table 2). In

parallel, asset risk in each rule is calculated, as for

CS1. In the end we have for each rule two values to

take into account for its remuneration, the weight of

the overheard Investor Agent and the risk of selected

asset. These two parameters will be combined with

the level of risk tolerance (TR) of the IA

TR = 1 – Risk (4)

The reward, as for CS1, is calculated differently

according to IA

does not tolerate any risk or when

it tolerates a certain percentage of risk. For IA

risk

averse, the reward is calculated as in (5):

Reward = 1 − (

R+

(

1−Pi

)

(5)

With Pi the weight of overheard Investor Agent. For

risk tolerant the reward is calculated as (6):

Reward = 1 − (

(

TR − R

)

(

1−Pi

)

(6)

OVERHEARING IN FINANCIAL MARKETS - A Multi-agent Approach

347

Both (5) and (6) reveal the follower nature of IA

introducing weight (Pi) of overheard Agents. More

Agent Investor heard is classified, its weight

increases more and more, and the reward of the rule

which tells us to follow it will increase. For IA

risk

averse, the formula shows that more the risk is

increasing more the reward diminishes and the rule

is poorly remunerated. For IA

risk tolerant, the

reward increases as the risk approaches the risk

tolerance. However, if the risk is greater than the

risk tolerance then the reward will be equal to 0.

CS1 and CS2 choose asset and direction based on

two information sources. CS1 is based on order

books while CS2 on overhearing the other agents.

6 SIMULATION RESULTS

Our system has been implemented in Java with

JADE as multi-agent platform and Oracle 10g as

DBMS. The classifiers have been programmed on

the basis of ART library. JADE incorporates

“Sniffer” agent to intercept agents’ behaviours.

Overhearing process is derived from the Sniffer. As

the Sniffer agent, an Overhearing Agent knows all

the agents and when they are created or deleted.

Time management (asynchronism of our system)

has been implemented at the beginning of simulation

with “Wait” instruction for a random period for each

investor agent then the sending of purchase or sale

orders through a specific JADE tickerbehaviour.

The market agent receives investor agents’

orders through a cyclicbehaviour. The simulation

begins with the introduction of assets, the degree of

risk tolerance, the number of each type of investor

agents, the number of agents to overhear as well as

the number of Overhearing Agents. Simulation

process start and purchase and sale transactions are

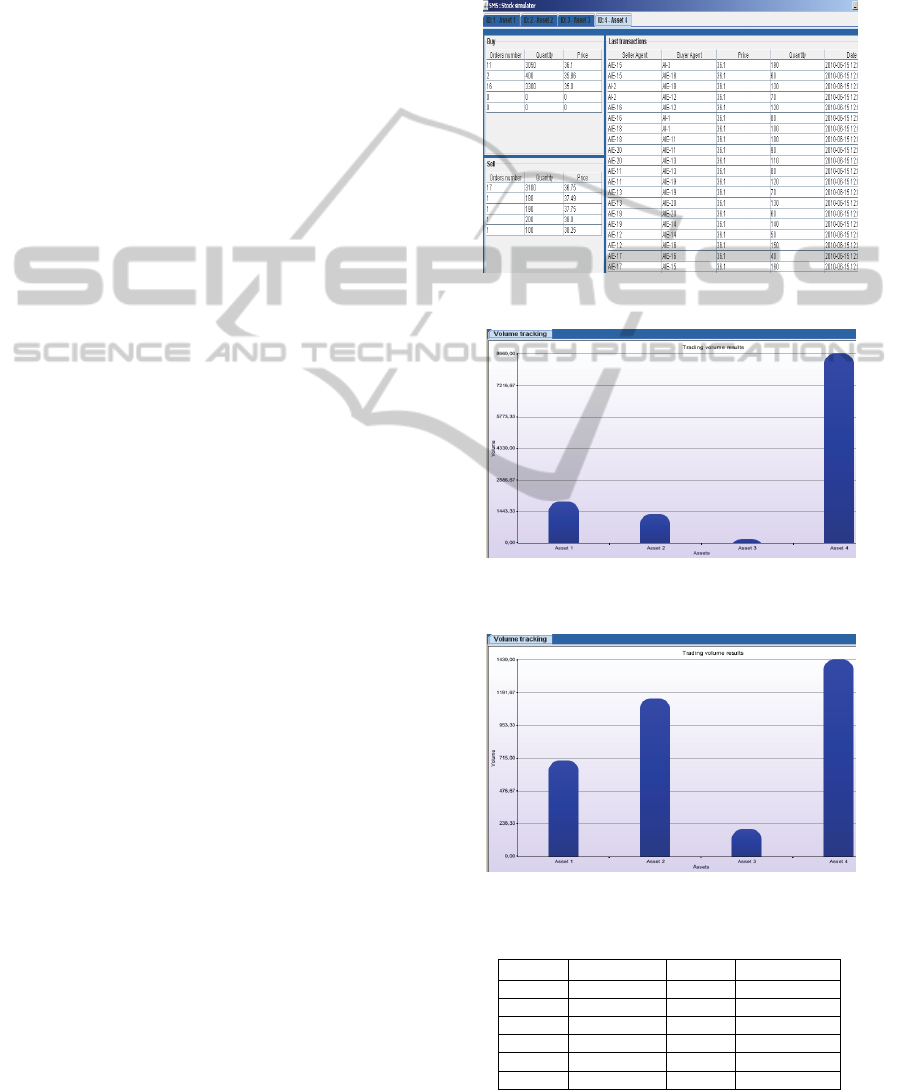
displayed by asset (Figure 6). Simulation is

conducted on 4 assets (Asset1 until Asset4), 3

Overhearing Agents and 20 investor agents.

We realize our simulations with two different

configurations. The first one is executed with 10 AI

and 10 AI

agents. The second one with 20 AI

agents (without overhearing). By the choice of these

two configurations we can observe the impact of

overhearing on the global evolution of the market.

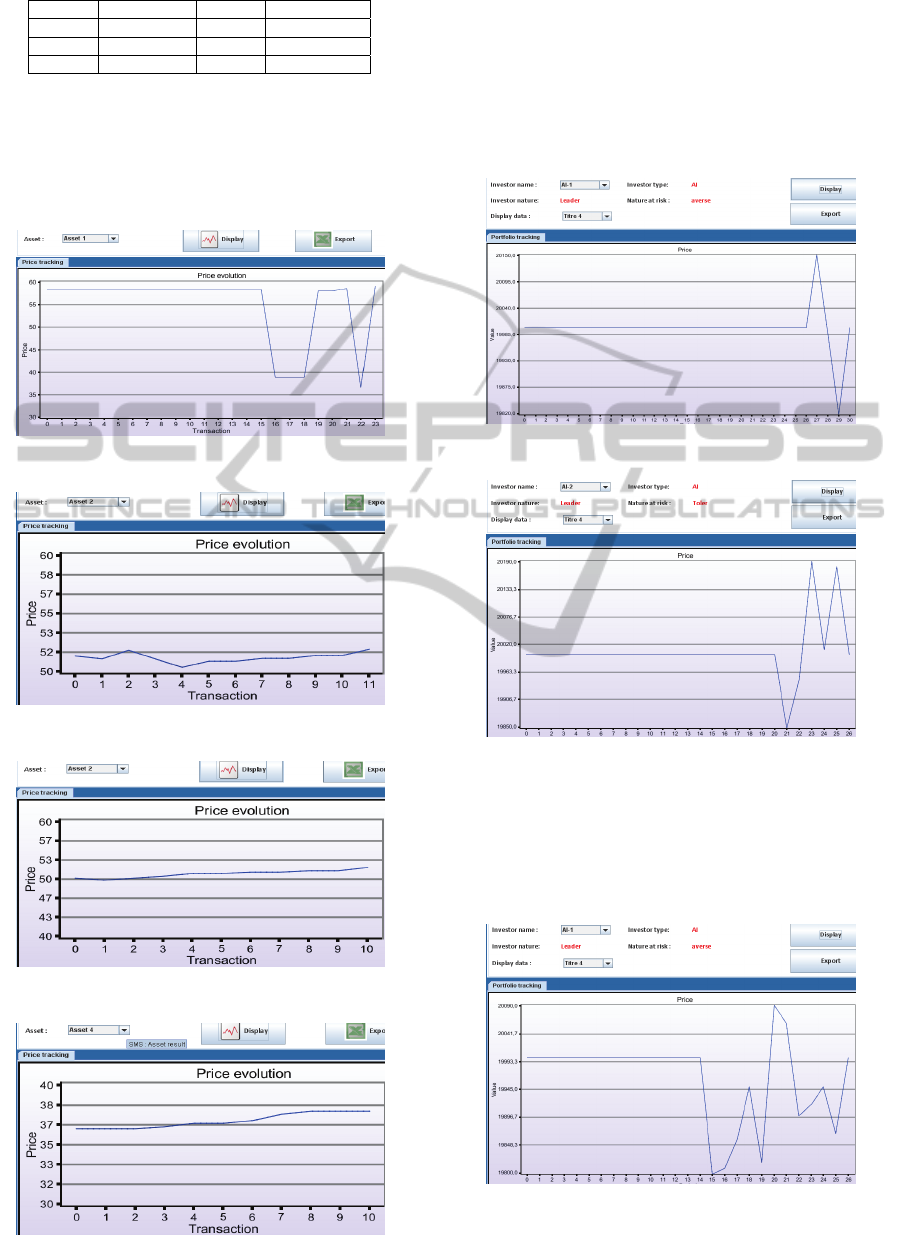
We notice in the model with overhearing that the

majority of agents are trading the same asset (Asset

4 in our simulation: Figure 7). It is not the same case

in the model without overhearing where agents are

trading in all the assets (Figure 8). We conclude that

overhearing create a disequilibria in the market.

The simulation allowed us to assess the agents’

activity degree by comparing their transactions. In

Table 3 we find that the agents based on overhearing

are less active than the others. It’s explained by the

several constraints involved in their decisions

(match desires with the trend, risk tolerance, etc.).

Figure 6: Simulation tracking Interface.

Figure 7: 4 assets trading volume in model with

overhearing.

Figure 8: Assets trading volume without overhearing.

Table 3: Number of transactions per agent.

Agent Transactions Agent Transactions

AI1 26 AIE11 9

AI2 20 AIE12 11

AI3 21 AIE13 14

AI4 31 AIE14 9

AI5 23 AIE15 10

AI6 0 AIE16 11

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

348

AI7 1 AIE17 4

AI8 0 AIE18 12

AI9 0 AIE19 10

AI10 18 AIE20 8

In our simulations, price evolution in the

configuration with overhearing (Figure 9, 10) is less

stable than that without overhearing (Figure 11, 12).

This allows us to deduce that the mimicry between

agents formalized by the introduction of overhearing

generates a high volatility in the market.

Figure 9: Asset 1 price evolution with overhearing.

Figure 10: Asset 2 price evolution with overhearing.

Figure 11: Asset 2 price evolution without overhearing.

Figure 12: Asset 4 price evolution without overhearing.

The portfolio evolution of investor agents in the

configuration without overhearing (Figure 13, 14) is

relatively stable compared to that of investor agents

in configuration with overhearing (Figure 15, 16,

17).

Figure 13: AI1 portfolio evolution without overhearing.

Figure 14: AI2 portfolio evolution without overhearing.

These results show that the instability of a

market is caused by the mimetism phenomenon. The

uncertain environment and the diversity of

information in the market generate a variety of

behaviours.

Figure 15: AI1 portfolio evolution with overhearing.

OVERHEARING IN FINANCIAL MARKETS - A Multi-agent Approach

349

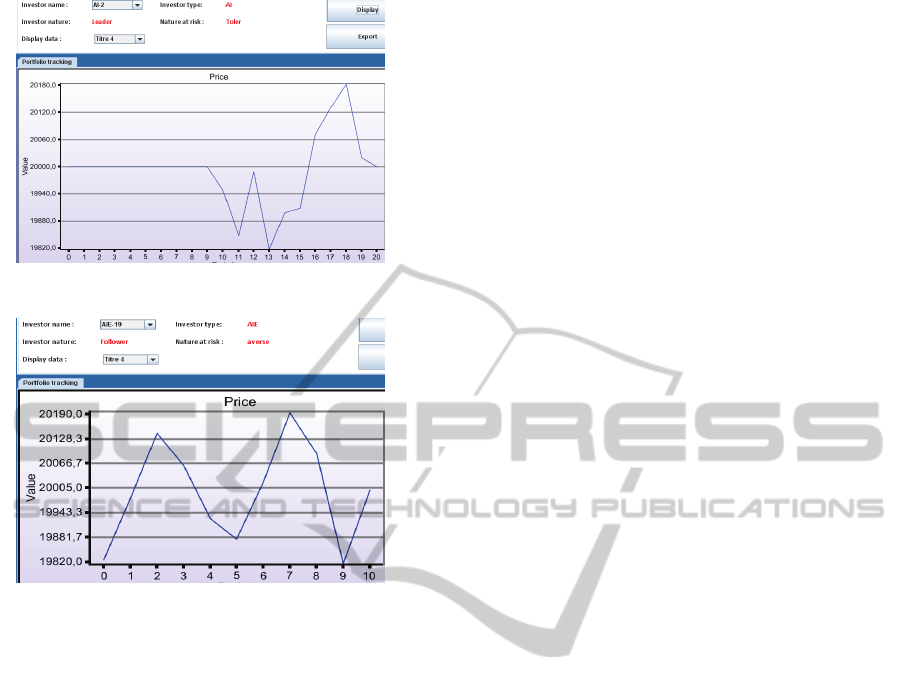
Figure 16: AI2 portfolio evolution with overhearing.

Figure 17: AIE19 portfolio evolution with overhearing.

The market liquidity i.e. there is at any time

purchasing and sales agents is maintained by agents

not based on overhearing according to the important

number of their transactions. If overhearing is

generalized in the market will certainly be less liquid

and more instable.

7 CONCLUSIONS

In this work, we have shown the need to simulate

financial markets in order to understand the

emergence of complex phenomena as unpredictable

as difficult to explain. We have analyzed different

existing models of artificial markets, and found that

most of them do not deal with order-driven financial

markets. In addition, these models do not pay

attention to the informal interactions between

investors. So we designed and implemented a new

model of order-driven markets, which operates

asynchronously and in which agents have been

endowed with sophisticated reasoning. The mental

models of the agents are supported by classifier

systems allowing them to learn from their

experiences and thereby improve their decisions.

These models have been tested, analyzed, and

proved their efficiency in finding the best behaviours

for investor agents. In addition, we have introduced

in our model an overhearing mechanism by offering

the opportunity to study the impact of informal

exchanged information in a financial market.

Through the proposed model, we have tested the

impact of overhearing on the global dynamic of the

market. We showed and discussed the results of

simulations and conducted experiments. Our

prototype can be extended and combined with a

social network structure for studying recurring

events in financial markets as speculative bubbles.

REFERENCES

Andersen, J., Sornette, D., 2003. The $-game, European

Physics Journal, pages 141–145.

Arthur, W. B., 1994. Inductive Reasoning and Bounded

Rationality, American Economic Review, 84(2).

Bak, P., Paczuski, M., Shubik, M., 1996. Price variations

in a stock market with many agents, arxiv.

Balbo, F., Maudet, N., Saunier, J., 2004. Interactions

opportunistes par l’écoute flottante, Université Paris-

Dauphine.

Buche, C., Septseault, C., De Loor, P., 2006. Proposition

d’un modèle générique pour l’implémentation d’une

famille de systèmes de classeurs, RSTI–RIA, 20(1).

Cincotti, S., Ponta, L., Pastore, S., 2006. Information-

based multi-assets artificial stock market with

heterogeneous agents, working paper, Geneva

University.

Derveeuw, J., 2008. Simulation multi-agents de marchés

Financiers, Thèse Doctorat de l’Université des

Sciences et Technologies de Lille.

Dugdale, J., Pavard, B., SOUBIE, J.L., 2000. A Pragmatic

Development of a Computer Simulation of an

emergency Call Center, In Cooperative Systems

Design, Frontiers in Artificial Intelligence and

Applications, Rose Dieng et al., IOS Press.

Holland, J. H., Holyoak, K. J., Nisbett, R. E., Thagard, P.

R., 1982. Classifier systems, Q-morphisms and

induction, In: Genetic Algorithms and Simulated

Annealing, ed. L. D. Davis.

Kotzé, Dr A. A., 2005. Stock Price Volatility: a primer,

Financial Chaos Theory.

LeBaron, B. L., Arthur, W.B., Palmer, R., 1999. Time

series properties of an artificial stock market, Journal

of Economic Dynamics and Control, 23, 1487–1516.

Legras, F., 2003. Organisation dynamique d’équipes

d’engins autonomes par écoute flottante, Thèse

doctorat, ONERA, Toulouse.

Markowitz, H. M., 1952. Portfolio Selection, Journal of

Finance, 7(1), 77–91.

Streichert F., Tanaka-Yamawaki M., Iwata M., 2006.

Effect of Moving Averages in the Tickwise Tradings in

the Stock Market. KES (3): 647-654.

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

350