GENDER VERIFICATION SYSTEM BASED ON JADE-ICA
Application to Biometric Identification System
Marcos del Pozo, Carlos M. Travieso, Jesús B. Alonso and Miguel A. Ferrer
Signals and Communication Department, Institute Technological for Innovation on Communication
University of Las Palmas de Gran Canaria, Campus Universitario de Tafiera, sn, 35017
Las Palmas de Gran Canaria, Spain
Keywords: Gender Classification, Verification System, Independent Component Analysis, Biometrics, Pattern
Recognition and Image Processing.
Abstract: Biometric systems are one of the hottest topics in technology research due their possibilities. An example of
these systems may be able to differ between male and female humans. This is called a gender classifier, and
it finds applications in areas such as security, marketing, or even as a reinforcement of other biometric
systems like face identification. In this work, a gender classifier system is modelled. The system implements
two different feature extraction algorithms based on Independent Component Analysis (ICA). On the other
hand, Support Vector Machines (SVM) is used as the classifier method. Finally, after 50 runs and 350
independent samples tested in each run, results give rise to an average of 82.40% of success working with
Joint Approximate Diagonalization of Eigen-matrices (JADE) ICA and SVM. Moreover, significant
differences between JADE-ICA and Fast-ICA algorithms have been pointed out, not only in terms of
success rate, but also in stability.
1 INTRODUCTION
Human faces are a huge source of information. They
provide information about age, gender, emotions,
attention, etc. It is easy to note that humans use this
information constantly, not only to recognize people
but for social behaviour as well. This means that it
can be very valuable information for fields such as
security, control systems, marketing, or automatic
interfaces.
Nowadays, Biometrics represents not only a very
important security application, but an important
business as well according to (Biometric
International Group, 2010) (see figure 1). Besides,
lots of applications are being developed around
humans. A gender identification would be an
important piece for these applications. Therefore, it
will be the focus of this work.
There are plenty of publications about gender
classification, combining different techniques and
models trying to increase the state of the art
performance. For example, (Jain and Huang, 2004)
uses a system based on the independent component
analysis (ICA) and a linear discriminant analysis
(LDA) to classify the gender. On the other hand,
(Jain and Huang, 2004) obtain better results
implementing a support vector machine (SVM)
along with ICA. In (Prince and Aghajanian, 2009)
and
(Xue-Ming and Yi-Ding, 2008), researches
apply Gabor filters to images. The obtained
characteristic feature vectors are then classified
using additive logistic models in (Prince and
Aghajanian, 2009), and a fuzzy SVM in
(Xue-Ming
and Yi-Ding
, 2008). As another technique, (Yiding
and Ning
, 2009) uses SIFT (Scale Invariant Feature
Transform) along with PCA to make the system
robust to scale factors or perspectives. Moreover,
shunting inhibitory convolutional neural networks
are used in (
Fok and Bouzerdoum, 2006) for both
feature extraction and classification. Finally, an
analysis of automatic gender classification and
psychological theories can be found in (Castrillon-
Santana and Vuong, 2007) using a system based on
principal component analysis (PCA) and SVM.
In (Jing-Ming et. al., 2010) presents an improved
Appearance-based Average Face Difference
(AAFD) scheme for face gender with a low
resolution and non-align thumbnail image. The
frontal face images in fa part and fb part of Feret
face database are employed, 1713 male and 1009
570
del Pozo M., Travieso C., Alonso J. and Ferrer M..
GENDER VERIFICATION SYSTEM BASED ON JADE-ICA - Application to Biometric Identification System.
DOI: 10.5220/0003297605700576
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (MPBS-2011), pages 570-576
ISBN: 978-989-8425-35-5
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

female, reaching 88.89%. Shape context based
matching was employed for classification (Tariq et.
al., 2009). The silhouetted face profiles in their
database were generated from the 3D face models.
The database had 441 images. The result for Gender
identification was 83.41% ± 2.56%. And for
Ethnicity identification for East and South East
Asians was 80.37 ± 3.8%.
The geometric features from a facial image are
obtained based on the symmetry of human faces and
the variation of gray levels, the positions of eyes,
nose and mouth are located by applying the Canny
edge operator (Ramesha et. al., 2009). The gender
and age are classified based on shape and texture
information using Posteriori Class Probability and
Artificial Neural Network respectively. The database
is composed on 1755 images from the FERET. It is
observed that face matching ratio is 100%, gender
classification is 95%, and age classification is 90%.
In (Aji et. al., 2009), the Kernel Principal
Component Analysis (KPCA) is used to extract the
feature set of male and female faces. A Gaussian
model of skin segmentation method is applied here
to exclude the global features such as beard,
eyebrow, moustache, etc. both training and test
images are randomly selected from four different
databases to improve the training. The database
(FERET, ORL, UMIST, AT&T) where used. 80
male and female faces where selected separately.
The results were between 85% and 92%.
This approach uses the rectangle feature vector
(RFV) as a representation to identify humans gender
from their faces (Bau-Cheng et. al., 2009). The
AdaBoost algorithm for feature selection was used.
The fa-part of Feret face database was used. In every
run, the size of training set was 1,408 (920 males
and 488 females) and the test set was 351 (230
males and 121females), reaching 92.42%.
Our proposal implements a gender classification
based on Independent Component Analysis (ICA)
methods. It aims to decompose an image, which
shows a face, on its different independent
components (ICs), and recover independent
unmixing sources with the gender characteristics.
Once this is done, ICs carrying gender information
are used in order to perform gender identification. A
supervised classification system is used to get an
automatic verification. Figure 2 shows diagram of
the proposed method.
For experiments, the database used is that
introduced on (Castrillon-Santana and Vuong,
2007). Thus, results obtained in this work will be
compared versus the (Castrillon-Santana and Vuong,
2007)’s results.
The remainder of this work is organized as
follows. Section 2 describes the database and its pre-
processing. In Section 3, the ICA methods are
introduced. The classifier system is presented on
section 4. Section 5 shows experiments, results and
discussions. And finally, conclusions, references and
acknowledgement are found in section 6.
Figure 1: Evolution of Biometrics Market between 2009
and 2014 according to (Biometric International Group,
2010).
Figure 2: Proposed approach.
GENDER VERIFICATION SYSTEM BASED ON JADE-ICA - Application to Biometric Identification System
571

2 DATABASE AND ITS
PRE-PROCESSING
The database used for the experiments was provided
by IUSIANI-ULPGC (Institute of Intelligent
Systems and Numerical Applications in Engineering
from University of Las Palmas de Gran Canaria)
(Castrillon-Santana and Vuong, 2007). It contains
1735 male samples and 1596 female samples. They
were collected from different sources such as videos
and internet pictures. Those samples ensure a wide
rank of image qualities, lightning conditions and
facial expressions.
Moreover, faces are presented in a frontal view,
or in an almost frontal view. They were manually
cropped and resized to dimensions 59x65 pixels.
Finally, an oval-like mask was applied to remove the
background. Figure 3 shows some samples of this
database.
Before feature extraction, two pre-processing
steps ware aplied. First, images were redimensioned
to specific smaller sizes. This allows simulations
with lower computational costs, and removes
redundant information from the higher resolution
images.
Figure 3: Some samples from the gender database.
Second, the histogram is equalized in order to
have images with similar characteristics. This
increases the success of the application by removing
intra-class differences and make it easyer for the
feature extractor block. Figure 4 shows the
progression of a samples along the pre-processing
chain.
Figure 4: The pre-processing block applied on a sample of
the (Castrillon-Santana and Vuong, 2007) database.
3 ICA METHODS
Independent component analysis (ICA) method is an
important tool in separating blind sources. The most
famous application of ICA is the cocktail party
problem. This case represents the problem of
separate independent voice sources from the mixing
voice dataset. However, in the present work, ICA is
used to extract base images from each sample, the
independent components (ICs). These allow the
system to remove useless information and focus on
important features.
In this paper, two different methods based on
ICA have been used as feature extraction. In
particular, FAST-ICA (Hyvärine et al., 2001)) and
Joint Approximate Diagonalization of Eigen-
matrices (JADE) ICA (Cardoso, 1999) have been
implemented.
Before continue introducing the mathematical
principles of each algorithm, it is important to
remember that sources must be mutually
independent and far away from the Gaussian
distribution in ICA methods.
3.1 Fast ICA
ICA has been widely used in signal processing. In
the field of image processing, it extracts information
in terms of ICs. It can be seen as a generalization of
the principal component analysis (PCA) procedure,
but instead of obtaining de-correlated components it
obtains ICs, which is a stronger condition. What
makes ICA different from other statistic methods is
its ability to find components that are statistically
independent and non-gaussian at the same time.
From a mathematical point of view, let
i
x with
i=1, 2…, N be some image samples, and assume that
these sample are linear combinations of
j
s with j=1,
2…, M
independent components. Also, lets denote
the matrixes
()
Τ
Ν21
x...,x,xX =
and
()
T
M
ss ...,,sS
21
=
.
Now, as expressed in (Hyvärine et al., 2001) the
relation between S and X can be modelled as
X=AS,
where
A is an unknown MxN matrix called the
mixing matrix. Moreover,
W can be defined as the
inverse of
A, so that S=WX. This W is the projecting
matrix and it is built out of the ICA coefficients.
When applied to images, ICA obtains base
images which are independent and not necessarily
orthogonal (Yi-qiong et al., 2004). These patches
contain information on the higher order statistics
connections between pixels. The obtained ICs are
shorted regarding the amount of information they
carry. Then, the number of ICs used to build the
projection matrix
W is automatically optimized by
the system, tacking first those with more
information.
Original Image Resize Equalization
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
572

3.2 JADE ICA
Joint Approximate Diagonalization of Eigen-
matrices (JADE) ICA approach is based on the
(joint) diagonalization of cumulant matrixes. For
simplicity, the case of symmetric distributions is
considered, where the oddorder cumulants vanish.
For random variables
X
1
,... , X
4
, and X
i
*
≝ X
i
−E(X
i
),
the second-order cumulants denoted as
C(X
1
,X
2
) are;
C(X
1
,X
2
) ≝ E(X
1
*
,X
2
*
)
(1)
And the fourth-order cumulants denoted as
C(X
1
,X
2
,X
3
,X
4
) are;
C(X
1
,X
2
,X
3
,X
4
) ≝ E(X
1
*
,X
2
*
,X
3
*
,X
4
*
) –
E(X
1
*
,X
2
*
)E(X
3
*
,X
4
*
) –
E(X
1
*
,X
3
*
)E(X
2
*
,X
4
*
) –
E(X
1
*
,X
4
*
)E(X
2
*
,X
3
*
)
(2)
In addition, the definitions of variance and
kurtosis of a random variable X are:
σ
2
≝ C(X,X) = E(X
*2
)
(3)
kurt(X) ≝ C(X,X,X,X) = E(X
*4
) –3E
2
(X
*4
)
(4)
Under a linear transformation
Y = AX, the
cumulants of fourth-order transformation is:
C(Y
i
,Y
j
,Y
k
,Y
l
) =
∑


C(

,

,

,

)

(5)
Since the ICA model (
X = AS) is linear, using
the assumption of independence by
C(S
p
, S
q
, S
r
, S
s
)
= kurt(S
p
)δ
pqrs
the cumulants of X = AS are obtained.
Where δ is defined as:


= 
1  ===
0 ℎ
(6)
and S has independent entries:
C(Y
i
,Y
j
,Y
k
,Y
l
) =
∑

(


)










(7)
with a
ij
the row i-th and column j-th entry of matrix
A.
Given any n × n matrix
M and a random n × 1
vector
X, we consider a cumulant matrix Q
x
(M)
defined by;
[

()] =  (, ,,)



(8)
If X is centered, the definition of Eq (2) shows
that:


(

)
=
(




)



−


(


)
−



−





(9)
where
tr(B) denotes the trace of matrix B and [R
X
]
ij
= C(X
i
,X
j
).
The structure of a cumulant
Q
x
(M) in ICA model
is easily deduced from Eq (7):


(

)
=
(

)



(

)
=(
(


)





1,…,

(


)





)
(10)
where
a
i
is the ith column of A, that is, A = [a
1
, . . . ,
a
n
].
Let
W be a whitening matrix, and Z ≝ WX. And
assume that the independent sources matrix S has
unit variance, so that S is white. Thus
Z = WX =
WAS
is also white, and the matrix U ≝WA is
orthonormal. Similarly, the previous technique can
be applied into Eq. (10) for any n × n matrix
M.
First, the whitening matrix
W and the cumulant
matrix
Z are estimated. Then, the estimation of an
orthonomal matrix
U, denoted by U, is calculated.
Therefore, an estimated matrix
A denoted by A is
obtained from
W
-1
U, and the sources matrix S is
calculated by
A
-1
X.
To measure non-diagonality of a matrix
B, off(B)
is defined as the sum of the squares of the non-
diagonal elements:

(

)
≝(

)



(11)
where b
ij
are elements of the matrix B. In particular
off
(U
T
Q
z
(M
i
)U) = offΔ
i
= 0 since Q
z
(M
i
) = UΔiU
T
and
U is orthogonal. For any matrix set M and
orthonormal matrix
V, the joint diagonality criterion
is defined as:


() ≝  (



(

))


∈
(12)
which measures diagonality far from the matrix
V
and bring the cumulants matrices from the set
M.
4 CLASSIFICATION SYSTEM
The main aspect of a Support Vector Machine
(SVM) is that it projects the problem into a higher
dimensional space where it can be solve linearly
(Travieso et al., 2004). This transformation is done
using an operator called kernel, in this case a Radial
Basis Function kernel (RBF-kernel). In the new
space, the positive and negatives classes are divided
GENDER VERIFICATION SYSTEM BASED ON JADE-ICA - Application to Biometric Identification System
573

using a linear function, which gives rise to a
boundary and a margin between both classes, as can
be seen in figure 5. Finally, a bi-class SVM (female
and male) with one-vs-one strategy has been
implemented for our experiments, in order to check
our algorithms.
Figure 5: Separate linear hyperplane in a SVM.
The SVM has used two input variables: a
normalization parameter (
SVMreg) and a kernel
parameter (
SVMker) linked to the width of RBF
function. These two parameters need to be optimized
to minimize error rate and maximize margin. A third
parameter, the threshold, is shifted until the false
positive rate equals the false negative rate. This
singular point is known as the equal error rate point
(EER).
5 EXPERIMENTS AND RESULTS
5.1 Experimental Methodology
The experimentation methodology used is based on
split the database on four different sets.
Training,
Validation and Test sets are applied during training
mode, and the
Blind set is used to obtain final
performance rates during test mode (see figure 2).
The
Training set is applied to the ICA algorithm
and the SVM classifier to obtain the system’s model
(projection matrix and classifier). The
Validation set
is then tested, and results are used to adjust the
classifier’s threshold to the EER point. Finally, the
Test set is used to test the system and obtain more
realistic results. These results are used by the
optimization algorithm to obtain the combination of
parameters (number of ICs,
SVMreg, and SVMker)
that maximizes success rate and stability. Once the
system is fully optimized, the test mode it activated
and the system is tested with the
Blind set to
measure its performance in a real scenario.
Experiments were repeated 50 times to ensure
the quality of the measure. Therefore, results are
shown in terms of mean and standard deviation.
Moreover, different configurations of the number of
samples used during the training mode and the
samples’ dimensions have been tested. Results from
training and test modes and computational times are
showed in the following sub-section.
5.2 Implementation
The experimental setting was developed to test the
evolution of the proposed system with respect to the
number of samples used for training. It is important
to mention that sample sets are made up randomly
per iteration.
The
Blind set is fixed to 350 male samples and
350 female samples. The number of samples used
for training mode was shifted between 600, 1200,
1800, and 2100 samples (half from each class). At
every stage, samples were randomly and equally
divided between
Training, Validation, and Test sets.
Evolution of results can be seen in tables 1 to 3.
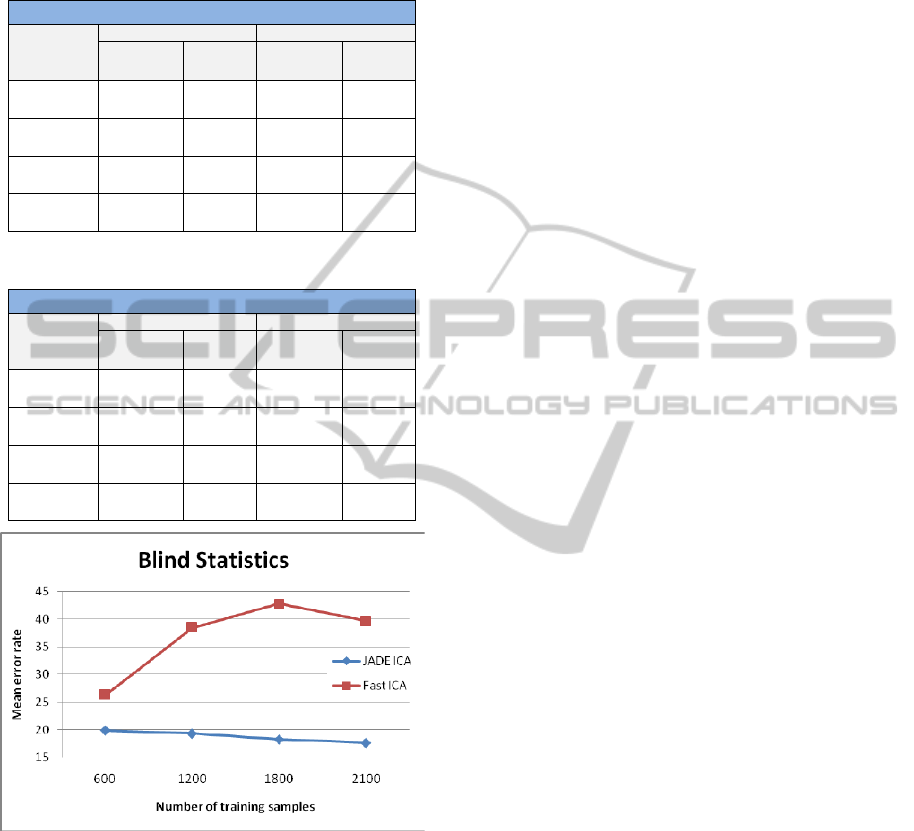
Results show how with JADE-ICA the system’s
performance increases with the number of training
samples. Therefore, best results are obtained with
JADE-ICA and 2100 samples, with a mean error rate
of 17.60%. This is not the case of Fast-ICA, which
best results are found with the minimum number of
training samples used, 600 training samples, with a
mean error rate of 26.30%. In general terms, JADE-
ICA outperforms Fast-ICA in every experiment in
terms of both performance and stability. This can be
seen graphically in figure 6.
Table 1: EER Results for the Validation set.
Validation Statistics
Samples for
Training Mode
JADE-ICA Fast-ICA
EER mean % ± std EER mean % ± std
600 19,24 % ± 3,06 25,96 % ± 4,76
1200 18,44 % ± 1,60 37,92 % ± 4,55
1800 17,65 % ± 1,86 65,06 % ± 18,72
2100 17,10 % ± 1,67 40,35 % ± 7,06
Moreover, because the number of ICs calculated
by JADE-ICA is limited to 20 for computational
reasons, the training process is faster than in Fast-
ICA; almost three times faster. This drives to the
fact that, in general terms, the optimal number of ICs
used by JADE-ICA is also lower than that used in
Fast-ICA, which makes the testing process faster as
well. For example, when 2100 samples ware used,
the computational time was about 81 milliseconds
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
574

for all 700 samples from the
Blind set. This makes a
testing time per sample of about 0.12 milliseconds.
Table 2: ER and FAR results for the Test set.
Test Statistics
Samples for
Training
Mode
JADE-ICA Fast-ICA
ER mean
% ± std
FAR
mean %
ER mean
% ± std
FAR
mean %
600
16,52 % ±
2,62
16,42 %
24,04 % ±
4,27
24,58 %
1200
17,97 % ±
1,93
17,37 %
36,35 % ±
4,38
37,57 %
1800
16,68 % ±
1,70
16,70 %
42,23 % ±
2,10
76.2 %
2100
16,14 % ±
1,77
16,04 %
37,64 % ±
1,86
39,66 %
Table 3: ER and FAR results for the Blind set.
Blind Statistics
Samples for
Training
Mode
JADE-ICA Fast-ICA
ER mean
% ± std
FAR
mean %
ER mean
% ± std
FAR
mean %
600
19,82 % ±
4,23
19,84 %
26,30 % ±
4,38
26,06
1200
19,28 % ±
1,58
19,05 %
38,42 % ±
4,21
39,46
1800
18,23 % ±
1,60
18,49 %
42,79 % ±
2,26
76,48 %
2100
17,60 % ±
1,91
17,57 %
39,65 % ±
2,11
41,62 %
Figure 6: Blind statistics in terms of mean error rate
shifting the number of samples used for training.
5.3 Discussion
Although both JADE-ICA and ICA are based in the
same principles, differences between algorithms
give rise to differences in performance. Results
show that in JADE-ICA algorithm reaches better
success rates under the same proposed system,
although the number of ICs calculated by the
algorithm was limited to 20 due to computational
reasons. Because the number of ICs used by Fast-
ICA was far bigger than 20 in general terms, it can
be expected that JADE-ICA can still improve by
increasing this limit.
JADE-ICA outperforms Fast-ICA in terms of
success rate. Moreover, the standard deviation
measures point out that JADE-ICA has a more stable
behaviour than Fast-ICA. In addition, the valance
between FAR and FRR is also more stable in JADE-
ICA.
All indicators show a better efficiency from
JADE-ICA algorithm. Therefore, it is possible to
state that the diagonalization of cumulant matrices
detect better gender features than the
orthogonalization of the negentropy. Making the
information recovered by JADE-ICA’s connectivity
matrix more discriminative.
Testing a system based on PCA and SVM,
(Castrillon-Santana and Vuong, 2007) achieved an
almost 80% of success rate with this database in a
full resolution situation; 59 x 65 pixels. Thus, based
on the results presented in this work JADE-ICA
outperforms PCA as well. However, in order to
directly compare results and quantify this
improvement, the same experimental procedure
must be executed.
6 CONCLUSIONS
This work presents a gender classification based on
JADE-ICA and a supervised SVM verifier as a
classification system. The best mean error rate
reached was 17.60%, achieved with 2100 training
samples (half from each class). In this case, the
standard deviation was 1.91, which highlights the
system’s stability. Moreover, this performance may
be improved by increasing number of training
samples. Finally, the computational time for testing
a sample was about 0.12 milliseconds in a quad-core
CPU with 2.66GHz and 3.00 GB of RAM. This
makes the system’s model a good candidate for real
time applications.
ACKNOWLEDGEMENTS
Authors want to thank Modesto Castrillón-Santana
from IUSIANI (University Institute of Intelligent
Systems and Numerical Applications in
Engineering) belongs to University of Las Palmas de
Gran Canaria (ULPGC), for allowing the use of the
database in order to test our algorithms.
GENDER VERIFICATION SYSTEM BASED ON JADE-ICA - Application to Biometric Identification System
575

This work has been partially supported by
“Catedra Telefónica – ULPGC 2009/10” (Spanish
Company), and partially supported by Spanish
Government under funds from MCINN TEC2009-
14123-C04-01.
REFERENCES
Aji, S., Jayanthi, T., Kaimal, M. R., 2009. Gender
identification in face images using KPCA. World
Congress on Nature & Biologically Inspired
Computing, 2009. pp. 1414-1418.
Bau-Cheng S., Chu-Song C., Hui-Huang H., 2009. Fast
gender recognition by using a shared-integral-image
approach. IEEE International Conference on
Acoustics, Speech and Signal Processing, pp.521-524.
Biometric International Group, 2010. Available: http://
www.biometricgroup.com/reports/public/market_repor
t.php
Cardoso, J. F., 1999. High-order contrasts for independent
component analysis, Neural Computation, 11(1), pp.
157—192
Castrillon-Santana, M., Vuong, Q. C., 2007. An Analysis
of Automatic Gender Classification, Lector Notes on
Computer Science, Springer, Vol. 4756, pp. 271-280.
Fok, H. C. T., Bouzerdoum, A., 2006. A Gender
Recognition System using Shunting Inhibitory
Convolutional Neural Networks, International Joint
Conference on Neural Networks, pp. 5336-5341.
Hyvärinen, A., Karhunen, J., and Oja, E., 2001.
Independent Component Analysis, Editorial Wiley-
Interscience.
Jain, A., Huang, J., 2004. Integrating independent
components and linear discriminant analysis for
gender classification, Proceedings Sixth IEEE
International Conference on Automatic Face and
Gesture Recognition, pp. 159-163, 17-19 May 2004
Jain, A., Huang, J., 2004b. Integrating independent
components and support vector machines for gender
classification, Proceedings of the 17th International
Conference on Pattern Recognition, vol.3, pp. 558-
561, 23-26 Aug. 2004
Jing-Ming, G., Chen-Chi, L., Hoang-Son, N., 2010. Face
gender recognition using improved appearance-based
Average Face Difference and support vector machine,
International Conference on System Science and
Engineering (ICSSE 2010), pp.637-640.
Prince, S. J. D., Aghajanian, J., 2009. Gender
classification in uncontrolled settings using additive
logistic models, Processing 16th IEEE International
Conference on Image, pp. 2557-2560, 7-10 Nov. 2009
Ramesha, K., Srikanth, N., Raja, K. B., Venugopal, K. R.,
Patnaik, L. M., 2009. Advanced Biometric
Identification on Face, Gender and Age Recognition.
International Conference on Advances in Recent
Technologies in Communication and Computing,
pp.23-27.
Tariq, U., Yuxiao, H., Huang, T. S., 2009. Gender and
ethnicity identification from silhouetted face profiles.
16th IEEE International Conference on Image
Processing, pp.2441-2444.
Travieso, C. M., Alonso, J. B., Ferrer, M. A., 2004. Facial
identification using transformed domain by SVM, in
38th IEEE International Carnahan Conference on
security Technology, pp. 321-324.
Xue-Ming, L., Yi-Ding, W., 2008. Gender classification
based on fuzzy SVM, International Conference on
Machine Learning and Cybernetics, vol.3, pp. 1260-
1264, 12-15 July 2008
Yiding, W., Ning, Z., 2009. Gender Classification Based
on Enhanced PCA-SIFT Facial Features, 1
st
International Conference on Information Science and
Engineering, pp. 1262-1265, 26-28 Dec. 2009
Yi-qiong, X., Bi-Cheng, L., Bo, W., 2004. Face
Recognition by Fast Independent Component Analysis
and Genetic Algorithm, Fourth International
Conference on Computer Information Technology, pp.
194-198.
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
576