Heritability Estimation Methods of Multiple Brain

Measures: A Preliminary MRI Study in Twins

Yu Yong Choi

and Kun Ho Lee

Department of Computer Engineering, Hanyang University, Seoul 133-605, Korea

Department of Marine Life Science, Chosun University, Gwangju 501-759, Korea

Abstract. Heritability is the proportion of total phenotypic variance due to

genetic influence. To estimate heritability, Falconer’s formula (FF) and

structural equation modeling (SEM) are used. However, compared to FF, SEM

is hardly applicable for neuroimaging analysis because the SEM tools such as

Mx cannot calculate numerous data simultaneously nor sequentially. We

developed a code for multiple calculations using Mx to estimate the heritability

of gray matter thickness at 81,924 surface points across the cerebral cortex.

Although FF and SEM provided similar results, SEM was inclined to yield

lower heritability estimates and more conservative significance than FF. In

considering the results, we propose that the correction for multiple comparisons

should be carefully performed for the results from SEM.

1 Introduction

Heritability is a fundamental notion in genetics that summarizes how much of the

variation in a trait among individuals is attributable to differences in genotype [3]. h

is used in reference to the proportion of total phenotypic variance due to genetic

influence. There are two representative methods for estimation of heritability:

Falconer’s formula (FF) and structural equation modeling (SEM). FF is based on the

difference between monozygotic (MZ) and dizygotic (DZ) twin correlations. In FF,

heritability is defined as

= 2(r

- r

) . (1

)

where r

is the MZ or identical twin correlation, and r

is the DZ or fraternal twin

correlation. SEM is based on decomposition of the phenotypic variance into the

genetic and environmental components. SEM defines heritability as

= V

/ V

. (2

)

where V

is the genetic variance and V

is the phenotypic variance.

Contrary to the simplicity of FF, the heritability estimation in SEM is a complex

process. Variance decomposition for estimation of the genetic variance requires

various sophisticated statistical methods such as a matrix algebra interpreter and a

numerical optimizer (e.g. Mx, or LISREL). The optimizer is used to minimize the

fitting function that denotes a discrepancy measure between the expected model and

the observed data. The iterative process of model fitting continues until the fitting

Choi Y. and Lee K..

Heritability Estimation Methods of Multiple Brain Measures: A Preliminary MRI Study in Twins .

DOI: 10.5220/0003305100820087

In Proceedings of the 2nd International Workshop on Medical Image Analysis and Description for Diagnosis Systems (MIAD-2011), pages 82-87

ISBN: 978-989-8425-38-6

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

function appears to reach the minimum. The SEM fit is so time-consuming that it is

not easy to apply to large-scale data like brain images that consist of numerous voxels.

Moreover, despite the increasing computational power of the modern computer, the

SEM software packages did not provide sequential as well as parallel processing

facilities that are necessary to manipulate numerous data together.

2 Methods

2.1 Approach

We decided to use the methodological heritage of genetic researchers as much as

possible. This approach could save a software developer time and labor, and would

enable a researcher to apply easily the methods in genetics to neuroimaging analysis.

Moreover, it could produce the reliable results to use the methods and tools verified in

the research field.

2.2 Software Development

Among the SEM software packages, Mx was chosen. The Mx developed by [9] is

widely used in human genetics, particularly twin studies because it facilitates

specification of complex models and mixture distributions and provides diverse

model fitting functions. To apply the SEM software Mx to neuroimaging analysis, we

write a MATLAB code for sequential processing of multiple data. The algorithm of

simple version of the program is below:

Array h[N], p[N];

for vertex=1 to N

read brain measures of all twins at the vertex;

write data for Mx;

execute Mx;

parse the result_in_text from Mx;

h[vertex] = the heritability value from the parsing;

p[vertex] = the p value from the parsing

end for

write h;

write p;

2.3 Twin Subjects

To measure the heritability of the brain structure, we recruited twin volunteers. The

study protocol was approved by the relevant institutional review boards (Seoul

National University, Catholic University of Korea), and written informed consent was

obtained from participants. A total of 40 healthy male twin volunteers aged 20.5 ± 1.9

(mean ± SD), consisting of 10 MZ and 10 DZ same-sex twin pairs, were recruited

from the community with advertisements. The MZ and DZ pairs were matched for

age (t = 0.23, P = 0.87) and sex. Blood or hair samples were taken at the date of

scanning or cognitive testing. Zygosity was determined by DNA analysis using the 15

highly polymorphic markers.

2.4 Image Acquisition and Analysis

From the twins, contiguous 0.9 mm axial MPRAGE images were acquired with a

1.5T MR scanner (Magnetom Avanto, Siemens) with TR=1160 ms; TE=4.3 ms;

flip=15; FOV=224 mm; matrix=512x512; number of slices=192; two images were

acquired and averaged. Anatomical images were corrected for intensity non-

uniformity [10], spatially registered to stereotaxic space [2], and masked to remove

extra-cerebral voxels. We used INSECT [11] to classify gray matter (GM), white

matter (WM), and cerebrospinal fluid (CSF).

For measuring gray matter thickness, the inner and outer cortical surfaces are

reconstructed [8]. These surfaces are automatically reconstructed by the Constrained

Laplacian-based Automated Segmentation with Proximities (CLASP) algorithm [6].

The cortical thickness was measured using the t-link method of calculating the

Euclidean distance between linked vertices on the white matter surface and the

GM/CSF intersection surface [5]. To compare thickness across subjects, the thickness

was spatially normalized. The vertices were transformed to the spherical model from

which the cortical surfaces originated, and nonlinearly registered to an standard

template on the sphere. A highly flexible deformation, in two dimensions, of a

template cortex to an individual was used for cortical surface registration. This

algorithm provided a transformation to match crowns of gyri between subjects using a

geodesic distance map. With this transformation, thickness information on the

vertices was transformed to the template. Then, diffusion smoothing, which

generalizes Gaussian kernel smoothing, with 30 mm FWHM (full width half

maximum) was used to increase the signal to noise ratio [1].

2.5 Statistical Analysis

To calculate the identical and fraternal twin correlations, we used the intraclass

correlation coefficient (icc) function of package psy in a statistical programming

environment R [4]. The statistical significance of the two twin correlations was

computed using Fisher’s z transformation.

For SEM, the conventional, univariate ACE model was adopted [9]. The ACE

model decomposes the phenotypic variance into additive genetic (A), shared

environmental (C), and non-shared environmental (E) variances. The statistical

significance of the genetic variance or h

was derived from chi-square difference

between ACE and CE models.

3 Results

To estimate heritability of a brain-based phenotype like gray matter thickness, both

FF and SEM were adopted and compared.

3.1 Falconer’s Formula

First, we applied FF to estimate the heritability of cortical thickness across the whole

brain. The MZ and DZ intracorrelations were derived the icc function of R. By the

equation 1 mentioned in the introduction, we computed and mapped heritability

estimates at surface points of the cerebral cortex (Fig. 1A). The statistical significance

of differences between the MZ and DZ intracorrelations were shown in Fig 1C.

3.2 Structural Equation Modeling

For SEM, the ACE structural equation model, a standard model for twin analysis, was

employed to determine what proportion of variance in a brain-based phenotype is

heritable (h

), versus the proportions which are due to shared environment or non-

shared environment. By fitting a univariate ACE model to each of 81,964 vertices

over the cerebral cortex, we produced high-resolution surface maps of the heritability

of brain structure in the twin sample (Fig. 1B). The statistical significances of the

heritability estimates were based on chi-square difference between ACE and CE

models (Fig. 1D).

Fig. 1. Heritability of gray matter thickness from Falconer’s formula (left) and from structural

equation modeling (right). The brain maps illustrated the heritability estimates (A and B) and

the statistical significance values (C and D) at eighty thousand or more vertices of the cerebral

cortex. P values are the statistical difference in intracorrelations between monozygotic and

dizygotic twins using Fisher’s z transformation (C) or chi-square difference between ACE and

CE models (D).

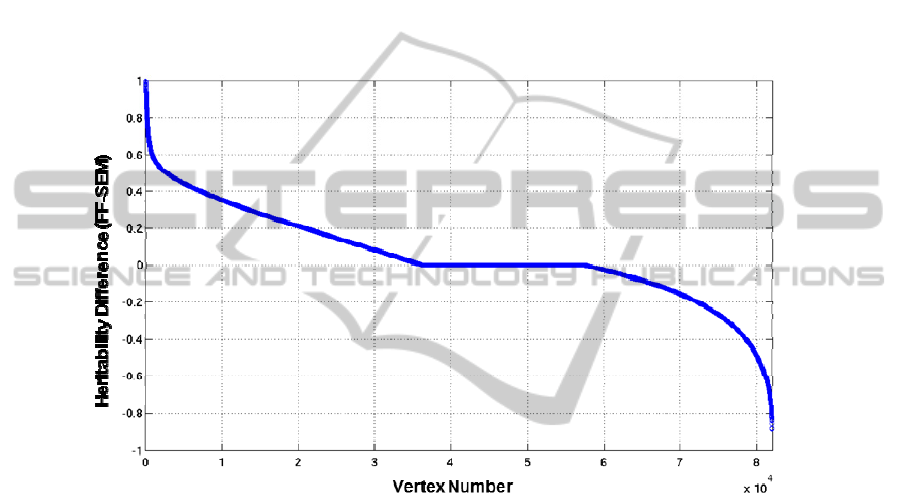
3.3 Comparison between Results from FF and from SEM

Genetic and environmental influences on gray matter thickness differed with cortical

regions (Fig. 1). The topological patterns of inherited regions were very similar

whether FF or SEM is employed. However, the results from SEM in Mx [9] tend to

be smaller and statistically conservative than Falconer’s estimation. The tendency also

is found in a previous study [7]. Precisely, 34.9% of all the vertices showed FF

heritability estimates larger than SEM ones by 0.1 or more, while only 18.9% did vice

versa (Fig. 2). At the other vertices (46.2%), the heritability differences were very

small (<0.1). In considering the results, the correction for multiple comparisons

should be carefully performed for the results from SEM.

Fig. 2. The heritability estimate differences between FF and SEM. The vertices on the whole

cortices are represented on the x axis and are numbered from 1 to 81,924. The y axis shows the

subtraction of SEM heritability estimates from FF heritability estimates.

4 Conclusions and Future Works

We presented a simple method to apply genetic analyzing tools for neuroimaging

researches. SEM analysis has many advantages over Falconer’s approach. Falconer’s

method provides nothing but heritability estimates, whereas SEM provides the

statistical significance as well as heritability estimates. Moreover, SEM can

distinguish shared and random environmental effects. Now, the proposed method

facilitates diverse and complex models that were used only in genetic research for

neuroimaging analysis including anatomical and functional MRI. In future, we will

apply multivariate SEM model for anatomical and functional neuroimaging analysis.

References

1. Chung, M. K., Worsley, K. J., Robbins, S., Paus, T., Taylor, J., Giedd, J. N., et al. (2003).

Deformation-based surface morphometry applied to gray matter deformation. Neuroimage,

18(2), 198-213.

2. Collins, D. L., Neelin, P., Peters, T. M., & Evans, A. C. (1994). Automatic 3D intersubject

registration of MR volumetric data in standardized Talairach space. J Comput Assist

Tomogr, 18(2), 192-205.

3. Falconer, D. S., & MacKay, T. F. C. (1996). Introduction to Quantitative Genetics (4th

ed.). Harlow, Essex, UK: Longman.

4. Ihaka, R., & Gentleman, R. (1996). R: A Language for Data Analysis and Graphics.

Journal of Computational and Graphical Statistics, 5(3), 299-314.

5. Kabani, N., Le Goualher, G., MacDonald, D., & Evans, A. C. (2001). Measurement of

cortical thickness using an automated 3-D algorithm: a validation study. Neuroimage,

13(2), 375-380.

6. Kim, J. S., Singh, V., Lee, J. K., Lerch, J., Ad-Dab'bagh, Y., MacDonald, D., et al. (2005).

Automated 3-D extraction and evaluation of the inner and outer cortical surfaces using a

Laplacian map and partial volume effect classification. NeuroImage, 27(1), 210-221.

7. Koten, J. W., Jr., Wood, G., Hagoort, P., Goebel, R., Propping, P., Willmes, K., et al.

(2009). Genetic contribution to variation in cognitive function: an FMRI study in twins.

Science, 323(5922), 1737-1740.

8. MacDonald, D., Kabani, N., Avis, D., & Evans, A. C. (2000). Automated 3-D extraction of

inner and outer surfaces of cerebral cortex from MRI. NeuroImage, 12(3), 340-356.

9. Neale, M. C., Boker, S. M., Xie, G., & Maes, H. H. (2003). Mx: Statistical Modeling (6th

ed.). VCU Box 900126, Richmond, VA 23298: Department of Psychiatry.

10. Sled, J. G., Zijdenbos, A. P., & Evans, A. C. (1998). A nonparametric method for automatic

correction of intensity nonuniformity in MRI data. IEEE Trans Med Imaging, 17(1), 87-97.

11. Zijdenbos, A. P., Forghani, R., & Evans, A. C. (2002). Automatic "pipeline" analysis of 3-

D MRI data for clinical trials: application to multiple sclerosis. IEEE Trans Med Imaging,

21(10), 1280-1291.