NEPs-Lingua: A New Textual Language to Program

NEPs

M. de la Cruz

, A. Jim´enez

, E. del Rosal

, G. Bel-Enguix

and A. Ortega

Departamento de Ingenier´ıa Inform´atica, Universidad Aut´onoma de Madrid, Madrid, Spain

GRLMC-Research Group on Mathematical Linguistics, Universitat Rovira i Virgili

Tarragona, Spain

Abstract.

Networks of Evolutionary Processors (NEPs) are one of the currently

most used new types of natural computers. This paper brieﬂy describes the model

and some developing tools for NEPs. Then, it describes NEPs-Lingua, a new

textual programming language for NEPs. Its two main goals are: reducing the size

needed by other representations and keeping the syntax as close as possible to the

one used to deﬁne NEPs in the literature. Some examples and future research

lines are also discussed.

1 Motivation

A great deal of research effort is currently being made in the so called “natural comput-

ing” realm. “Natural computing” is mainly focused on the deﬁnition, formal descrip-

tion, analysis, simulation and programmingof newmodels of computation (usually with

the same expressive power as Turing Machines) inspired by Nature. Their bio-inspired

nature makes these models specially suitable for the simulation of complex systems.

Some of the best known natural computers are Lindenmayer systems (L-systems, a

kind of grammars with parallel derivation), cellular automata, DNA computing, genetic

and evolutionary algorithms, multi agent systems, artiﬁcial neural networks, P-systems

(computation inspired by membranes) and NEPs (or networks of evolutionary proces-

sors). This paper is devoted to this last model.

There are two main areas in which these models could be useful: as new architec-

tures for computers, different from von Neumann’s machine; and as modelling tools

to simulate complex systems for which “conventional approaches” (usually based on

differential equations) are, in practice, difﬁcult to handle.

Two steps are needed in both scenarios: 1) design a particular instance of the consid-

ered model able to solve the task under study (this step is equivalent to “programming”

the model) and 2) “run” the model.

This work was partially supported by the R&D program of the Community of Madrid

(S2009/TIC-1650, project “e-Madrid”) as well as by MTM 2007-63422. The authors thank

Dr. Manuel Alfonseca for his help to prepare this document.

de la Cruz M., Jiménez A., del Rosal E., Bel-Enguix G. and Ortega A..

NEPs-Lingua: A New Textual Language to Program NEPs.

DOI: 10.5220/0003308200370046

In Proceedings of the 1st International Workshop on AI Methods for Interdisciplinary Research in Language and Biology (BILC-2011), pages 37-46

ISBN: 978-989-8425-42-3

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

Several attemps have been made to build hardware devices to support these bio-

inspired models. Some research groups are currently implementing in silico the basic

components of P-systems [4]. [9] describes other examples of hardware implementa-

tions of cellular automata, CAM-6 and its derivatives, that have been used for the simu-

lation of complex systems (see [8]). But, unfortunately there are no real computers for

almost all bio-inspired models. So, step 2 usually implies the simulation of the model

in a “conventional” (von Neumann) computer.

Informally, and assuming that NP (nondeterministic polynomial time) 6= P, NP is a

complexity class that includes those problems whose solution by means of algorithms

run on conventional computers requires more than polynomial time. We can informally

understand more than polynomial as exponential. One of the most interesting features

of these bio-inspired computers is their intrinsic parallelism. We can design algorithms

for them that could improve the exponential performance of their classic versions. Nev-

ertheless, when the models have to be simulated on conventional computers, the total

amount of space needed to simulate the model and to actually run the algorithm usually

becomes exponential. This may be one of the main reasons why natural computers are

not widely used to solve real problems. Most of the simulators are not able to handle

the size of non trivial problems. Grid, cloud computation and clusters offer an inter-

esting and promising option to overcome the drawbacks of both solutions: “speciﬁc”

hardware, and simulators run on von Neumann’s machines.

There are several research groups interested in programming tools for natural com-

puters. These tools include textual and visual programming languages, compilers, se-

quential and parallel simulators.

P-Lingua ([5] and http://www.p-lingua.org) is a programming language for

membrane computing which aims to be a standard to deﬁne P systems. One of its main

characteristics is to remain as close as possible to the formal notation used in the liter-

ature to deﬁne P systems. Once he has formalized his P systems, the programmer does

not need any additional effort to describe them with P-Lingua. P-Lingua is also the

name of a software package that includes several built-in simulators for each supported

model, as well as the compilers needed to simulate P-Lingua programs.

One of the current topics of interest of the authors of this paper is the development of

programming tools for NEPs, which will be brieﬂy described in the following sections.

The current paper introduces NEPs-Lingua, the ﬁrst textual programming language for

NEPs. It is a ﬁrst step to extend the P-Lingua approach to other bio-inspired models

of computation. Our goal is to provide the researchers with a homogeneous family of

languages for programming natural computers. The programmer familiar with a model

will not have to learn a very different syntax if he tries to use other models. This is the

reason why NEPs-Lingua is designed to be similar to P-Lingua. NEps-Lingua has two

main goals that will also be described in detail later: 1) Like P-Lingua, it aims to provide

the researchers with a syntax as close as possible to the one used to describe NEPs in

the literature. 2) It tries to ease some usually boring, mechanical and time-consuming

tasks needed to describe NEPs with the input formalisms of the available tools.

2 NEPs

A Network of evolutionary processors (NEP [1]) can be deﬁned as a graph whose nodes

are processors which perform very simple operations on strings and send the resulting

strings to other nodes. Every node has ﬁlters that block some strings from being sent

and/or received.

NEPs-Lingua also support PNEPs (Parsing NEPs), an extension to NEPs introduced

in [7] to handle context free grammars.

NEPs and PNEPs: Deﬁnitions and Key Features. Following [1] we introduce the

basic deﬁnition of NEPs.

Deﬁnition A Network of Evolutionary Processors of size n is a construct:

Γ = (V, N

, N

, ..., N

, G),

where:

– V is an alphabet and for each i with 1 ≤ i ≤ n,

– N

= (M

, A

, P I

, P O

) is the i-th evolutionary node processor of the network.

The parameters of every processor are:

• M

is a ﬁnite set of evolution rules of just one of the following forms:

i. a → b, where a, b ∈ V (substitution rules),

ii. a → ε, where a ∈ V (deletion rules),

iii. ε → a, where a ∈ V (insertion rules),

iv. a → s, where a ∈ V , s ∈ V

∗

(context free rules applied to change a

symbol by a string) PNEPs replace substitution rules by this kind of rules.

PNEPs add this kind of rule to reduce the amount of equivalentderivations.

• A

is a ﬁnite set of strings over V . The set A

is the set of initial strings in the

i-th node.

• P I

and P O

respectively representing the input and the output ﬁlters. These

ﬁlters are deﬁned by the membership condition, namely a string w ∈ V

∗

can

pass the input ﬁlter (the output ﬁlter) if w ∈ P I

(w ∈ P O

). In this paper we

will use two kind of ﬁlters:

∗ Those deﬁned as two components (P, F ) of Permitting and Forbidding

contexts (a word w passes the ﬁlter if ( alphabet of w ⊆ P )∧(F ∩ alphabet

of w = ∅)).

∗ Those deﬁned as regular expressions r (a word w passes the ﬁlter if w ∈

L(r), where L(r) is the language deﬁned by the regular expression r).

– G = ({N

, N

, . . . , N

}, E) is an undirected graph called the underlying graph of

the network. The edges of G, that is the elements of E, are given in the form of sets

of two nodes. The complete graph with n vertices is denoted by K

Further formal details on the way in which NEPs evolve can be found in [1].

3 Programming Tools for NEPs

The authors of this paper have proposed a development environment for programming

NEPs that includes a Java NEP simulator (jNEP), a Java graphical viewer of its sim-

ulations (jNEPview), and a domain speciﬁc visual language for NEPs designed with

AToM

(NEPVL) In the following paragraphs we will brieﬂy introduce these modules.

NEPs-Lingua and its compilers will be integrated in this environment as its textual pro-

gramming language.

jNEP and jNEPview. jNEP [3] reads the deﬁnition of the NEP from an XML conﬁgu-

ration ﬁle that contains special tags for any relevant components in the NEP (alphabet,

stopping conditions, the complete graph, every edge, the evolutionary processors with

their respective rules, ﬁlters and initial contents). Despite the complexity of these XML

ﬁles, the interested reader can see that the tags and their attributes have self-explaining

names and values.

We show below, as an example, the conﬁguration ﬁle of a very simple NEP. It has

two nodes that, respectively,delete and insert the symbol B. The initial word AB travels

from one node to the other. The ﬁrst node removes the symbol B from the string before

leaving it in the net. The other node receives the string A and adds again the symbol

B. The resulting string comes back to the initial node and the same process takes place

again.

<EVOLUTIONARY_PROCESSORS>

<EVOLUTIONARY_RULES>

<RULE ruleType="deletion" actionType="RIGHT" symbol="B"

newSymbol=""/></EVOLUTIONARY_RULES>

<FILTERS> <INPUT type="2" permittingContext="A_B"

forbiddingContext=""/>

<OUTPUT type="2" permittingContext="A_B"

forbiddingContext=""/></FILTERS>

</NODE>

<EVOLUTIONARY_RULES>

<RULE ruleType="insertion" actionType="RIGHT" symbol="B"

newSymbol=""/> </EVOLUTIONARY_RULES>

<FILTERS> <INPUT type="2" permittingContext="A_B"

forbiddingContext=""/>

<OUTPUT type="2" permittingContext="A_B"

forbiddingContext=""/></FILTERS>

</NODE>

</EVOLUTIONARY_PROCESSORS>

<STOPPING_CONDITION>

</STOPPING_CONDITION>

</NEP>

(XML conﬁguration ﬁle for a simple NEP with just two processors that send the words A and B

back and forth)

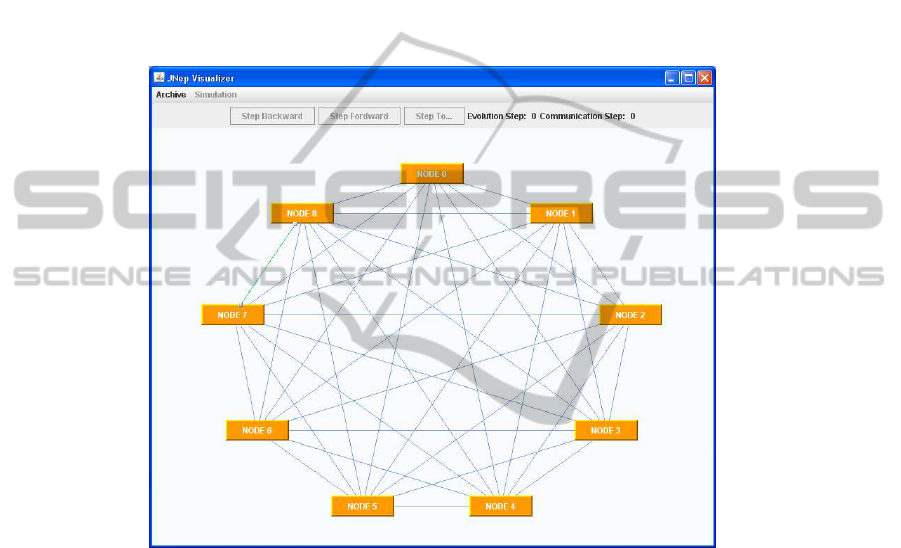
Figure 2 contains, as an example, the windows used by jNEPview to show the net-

work topology of one of the NEPs under study. Further details on jNEPview can be

found in [2].

NEPVL. AToM

is a python platform to develop domain speciﬁc visual languages. We

have used it to design NEPVL.

Fig.1. NEPVL program for the NEP with two processors.

Figure 1 shows the NEPVL program that deﬁnes the same NEP with two processors

previously described. Further details about AToM

and NEPVL can be found in [6].

4 The NEPs-Lingua Syntax

In the following paragraphs we describe, mainly by examples, the syntax of NEPs-

Lingua. A full ANTLR

description of the complete grammar may be asked from the

authors. The main components of a NEPs-Lingua program are atomic data, comments,

nodes, the alphabet, the initial contents of the nodes, evolutionary rules, ﬁlters, the

connections of the NEP graph and stopping conditions.

Atoms. There are two classes of atomic data: alfanumeric strings of symbols (they have

to start with an alphabetic character); and integer arithmetic expressions, with the usual

mathematical notation, that include the operators in the set {∧(power), +, −, ∗, /}

Comments. The typical C++ comments are also available in NEPs-Lingua.

ANTLR is a Java tool to design top-down parsers and language processors, developed by

Terence Par. Further information can be found at http://www.antlr.org/

Line Comments. For example // Comment.

The comment includes every symbol until the end of the line.

Multi Line comments. For example

... Comment

...

Where the comment includes everything (even the end of line markers) between the

symbols “/*” and “*/”.

Alphabet. It is the alphabet of the NEP, a set of strings of symbols. The expression

@A={X,S,a,b,o,O} deﬁnes an alphabet that contains the elements “X”, “S”, “a”, “b”,

“O”, and “o”.

Nodes. This is the most complex type of NEPs-Lingua data. There are two classes of

nodes: with and without indexes. There are two kinds of indexes: numeric (deﬁned by

a range) and symbolic (deﬁned by a set of strings of symbols). The syntax of indexes

with numeric ranges is borrowed from P-Lingua.

Non Indexed Nodes. The expression {initial, final} deﬁnes two nodes without

indexes with names initial and ﬁnal.

Indexed Nodes. The example deﬁnes a family of nodes with two indexes. One of them

(i) takes its values from the interval [0, 10]. The values of the other (j) are taken from

the set {o, a, b}.

{m{i,j}: 0<=i<=10, j->{o,a,b}}

The explicit set of the 33 deﬁned nodes is {m

0,a

, m

0,b

, m

0,c

, . . . m

10,a

, m

10,b

, m

10,c

Different kinds of nodes can be mixed by means of the union operator. The next

example shows the deﬁnition of a set of nodes that contains the two previous examples.

@N={initial, final}+{m{i,j}: 0<=i<=10, j->{o,a,b}}

Initial Content. It describes the set of strings that a given node initially contains.

Notice that the node is written as a parameter of the content directive @c. The expression

@c{n{X}} = {X, S} sets the initial content of the node n

to {X, S}

Rules. Each type of rule has a different notation. Notice that, as in P-Lingua, the symbol

# stands for the empty string and the string --> separates the left and right sides of

the rule. The sentences # -->a, a --># and S-->aSb are examples of respectively

insertion, deletion, and substitution (or deriving) rules.

All the rules for a given node are given together in the same sentence. The sentence

@r{n{S}} = {S-->aSb, S-->ab} assigns two deriving rules to the node n

Filters. Each processor needs an input and an output ﬁlter. Different papers previously

mentioned deﬁne three components in the ﬁlters: their type and the permitting and for-

bidding contexts. We have grouped the different ﬁlters of the literature in six types

(depending on the way in which they are applied): types from 1 to 4 and ﬁlters deﬁned

by means of regular expressions or by means of sets of strings. Both contexts are just

sets of symbols described by means of regular patterns or explicit sets of strings. The

following examples deﬁne several ﬁlters:

@pif{n{S}}= {1, {abc, oo}}

@fof{initial} = {@regular_pattern, ( ((a[]b)+) ][ (c

) )][ # }

@pif{n{2,a}}= {@set, {a,ab,aabb}}

where @pif and @fof stand respectively for permitting input and forbidding ouput

ﬁlter (the same for forbiddinginput and permitting output ﬁlters). In regular expressions

[], ][, +,

, # represent intersection, union, + and *, and the empty string.

Connections. This element makes it possible to get a compact representation of NEPs.

There are two ways of deﬁning connections: the directive @complete, that stands for a

complete graph; and an explicit set of connections deﬁned by means of pairs of nodes.

The next examples show both options:

@C=@complete

@C={ (final,n{X}), (n{X},m{9,a}) }

Stopping conditions. The stopping conditions are written in a set after the directive

@S. Each kind of condition is represented by its name and its required parameters. Both

names and parameters are easy to identify in the following example:

@S={@no_change, @max_steps = 3+4, @non_emtpy_node={n{O}, n{X}} }

where @no_change stands for two consecutive equal conﬁgurations; @max_steps re-

quires an expression to deﬁne the number of steps (the NEP stops after taking the given

number of steps); and @non_empty_node includes a set of nodes whose contents are

initially empty (the NEP stops when one of these nodes receives some string).

5 Examples

In this section we will show some complete NEPs-Lingua programs. Our main goal is to

highlight the two main characteristics of NEPs-Lingua: reducing the size and keeping

close to the formal notation. For this purpose we will compare several NEPs-Lingua

programs with NEPs examples taken from the literature. For space reasons, we refer to

the original papers for the detailed deﬁnition of the examples.

Reducing the Size of the Representations. First we show the NEPs-Lingua program

for the example with two processors previously described. We can appreciate with this

simple example that the NEPs-Lingua program is more compact than the other two

representations (see the corresponding XML source and ﬁgure 1).

@A={A,B}

@N={ n{i}: 0 <= i <= 1}

@c{n{0}}={A,B}

@r{n{0}}={B-->#}

@r{n{1}}={#-->B}

@S={@max_steps = 8 }

@C={@complete}

The reduction in size is greater as the complexity of the NEP increases. NEPs usu-

ally have complete graphs.

Fig.2. NEPVL program for the NEP that solves the 3 SAT problem.

Figure 2 shows the jNEPview window for a NEP with a complete graph with 9

nodes.

The XML conﬁguration ﬁle for this NEP is forced to explicitly contain all the

nodes and connections(see the XML sample previously shown) while the NEPs-Lingua

source has to contain just the following two sentences:

@N={ n{i}: 0 <= i <= 8}

@C=@complete

[1] shows a NEP able to solve a small instance of the well known graph coloring

problem with three different colours. It needs a complete graph with more many nodes

than in the previous example.

The jNEPview window for this NEP is not shown in this paper because it is difﬁcult

to handle: it looks like a ball of yarn. Once again the NEPs-Lingua program needs just

the following two sentences:

@N={ n{i}: 0 <= i <= 50 } \\ Definition of 51 nodes

@C=@complete

Keeping NEPs-Lingua as Close as Possible to the Formal Notation used in the Lit-

erature. The interested reader can easily see in the references for the last two examples

(3-SAT and 3 coloring) that NEPs-Lingua syntax is mainly inspired by the formal no-

tation used in the literature to describe NEPs.

[7] contains another example: a NEP associated with the context free grammar for

axiom X with the derivation rules {X → SO, S → aSb, S → ab, O → o, O →

oO, O → Oo}

It is easy to see that the following NEPs-Lingua program for this NEP is quite

similar to its formal deﬁnition.

@A={X,S,a,b,o,O} // Alphabet

@N= {final}+ {n{symbol}:symbol->{X,S,O}} /

Nodes associated

with non terminal symbols

@c{n{X}}={X} // Initial content of the axiom node

@r{n{X}}= {X-->SO} // Deriving rules for the axiom

@r{n{S}}= {S-->aSb, S-->ab}

@r{n{O}}= {O-->o, O-->oO, O-->Oo}

@C=@complete // The graph is complete

@S={ @non_emtpy_node={final} } // Stopping conditions

6 NEPs Lingua Semantics

The semantic constraints that every NEPs-Lingua program has to satisfy are outlined

below:

– It has to contain exactly one alphabet and one set of node declarations.

– It needs at most one of the following elements:

• Connection declaration set. By default, the graph is considered complete.

• Set of stopping conditions. @no_change is assumed by default.

– Filters, rules and initial contents are optional.

– Nodes have to be deﬁned before their use.

– Each symbol representing rules, ﬁlters and initial contents has to be included in the

alphabet.

NEPs-Lingua compilers should ensure these conditions. The usual way of control-

ling the last one is by means of a symbol table that is ﬁlled while processing the decla-

ration sentences and is consulted by the sentences that use nodes and symbols.

We have used different Hashtable Java objects to check these constrains.

The following example shows some semantic mistakes:

@A={A}

@N={ n{i}: 0 <= j <= 1}

@c{n{0}}={A,B}

@r{n{0}}={B-->#}

@r{n{2}}={#-->B}

@S={@max_steps = 8 }

@C={@complete}

– The third, fourth and ﬁfth lines contain the symbol B, which is not in the alphabet.

– The second line deﬁnes the index j, while the declared one is i

– The ﬁfth line deﬁnes the rules for the node n

, but the value for index (2) is invalid

7 Further Research Lines

Code Generators. In the future we intend to provide our system with some code gen-

erators. The ﬁrst one will translate NEPs-Lingua programs into the XML conﬁguration

ﬁles that jNEP uses as input. It could also be used to generate the same python programs

that the NEPVL software uses.

Extensions. Although this simple syntax seems to be expressive enough for the NEPs

we have found in the literature, we are considering the following extensions, usually

present in programming languages: global variables and parametrized sub-NEPs.

References

1. J. Castellanos, C. Mart´ın-Vide, V. Mitrana, and J. M. Sempere. Networks of evolutionary

processors. Acta Informatica, 39(6-7):517–529, 2003.

2. M. Cu´ellar and E. del Rosal. jnepview: a graphical trace viewer for the simulations of neps.

3. E. del Rosal, R. Nu˜nez, C. Casta˜neda, and A. Ortega. Simulating neps in a cluster with jnep.

In Proceedings of International Conference on Computers, Communications and Control, IC-

CCC 2008,, 2008.

4. L. Fern´andez, V. J. Mart´ınez, and L. F. Mingo. A hardware circuit for selecting active rules in

transition p systems. In Seventh International Symposium on Symbolic and Numeric Algo-

rithms for Scientiﬁc Computing (SYNASC 2005), 2005.

5. M. Garc´ıa-Quismondo, R. Guti´errez-Escudero, M. A. Mart´ınez del Amor, E. Orejuela, and

I. P´erez-Hurtado. P-lingua 2.0: A software framework for cell–like p systems. International

Journal of Computers, Communications and Control, IV(3):234–243, 2009.

6. A. Jim´enez, E. del Rosal, and J. de Lara. A visual language for modelling and simulation

of networks of evolutionary processors. In Trends in Practical Applications of Agents and

Multiagent Systems, Advances in Soft Computing.

7. A. Ortega, E. del Rosal, Diana P´erez, R. Mercas¸, A. Perekrestenko, and M. Alfonseca. PNEPs,

NEPs for Context Free Parsing: Application to Natural Language Processing, pages 472–479.

LNCS. 2009.

8. M. A. Smith and Y. Bar-Yam. Cellular automaton simulation of pulsed ﬁeld gel electrophore-

sis. ELECTROPHORESIS, 14(1):1522–2683, 1993.

9. T. Toffoli and N. Margolus. Cellular Automata Machines. MIT Press, London, 1987.