IMAGE CAPTURE FOR CONCRETE PROGRAMMING

Building Schemata for Problem Solving

Vladimir Estivill-Castro and Brendan Bartlett

Grifﬁth University, Brisbane, Australia

Keywords:

Information technologies supporting learning, Software tools.

Abstract:

Problem solving in IT consists of expressing an algorithm for abstract models of computation. This has proven

to be hard, but it can be taught, specially when students are exposed to concrete and visual illustrations of

artefact behaviour. IT graduates require problem-solving skills, but it is difﬁcult to teach such problem-solving

skills in the context of huge bodies of technological concepts, large programming languages and the need for

system-focused courses required for accreditation. We propose to design and develop concrete programming

activities that will enable to articulate problem solving across many subjects. The goal is also to place concepts

in the context of concrete problems, and to progress from concrete settings (where programming is achieved

by building structures) to visual settings (where programming is achieved by re-arranging icons in a GUI), and

later to textual programming in imperative APIs like

MaSH

. We capture the participants constructions with a

camera and this is a program that produces behavior. The approach delivers the potential to take students to

investigate research questions.

1 INTRODUCTION

Students graduating from Information and Communi-

cation Technology degrees should be able to perform

problem solving by expressing the solution algorith-

mically. The ability to solve problems with a degree

of creativity is highlighted as an essential characteris-

tic for both novice undergraduate engineers and qual-

iﬁed IT professionals in benchmarks published by the

OECD (Houghton, 2004). Problem solving is cru-

cial to the professional success of graduates of the

School of Information and Communication Technol-

ogy at Grifﬁth University, Australia. It is usually man-

ifested by the ability to program a computer so that,

from any set of input values that constitute a valid in-

stance of the problem, the computer ﬁnds out the solu-

tion to such instance. In fact, such abilities are consid-

ered relevant even from high-school. Under the label

of “Working ways” high-school students in Queens-

land are expected to

• plan activities and investigations to explore con-

cepts,

• plan strategies to solve mathematical questions,

problems and issues,

• evaluate thinking and reasoning,

• perform thinking and working and reasoning that

can be applied to solve problems in real-life and

abstract investigations.

Problem solving for IT graduates means not only

solving problems (Dewar, 2006), but also express-

ing a method, an algorithm, in the language that de-

ﬁnes the operation of an automaton (Dale and Weems,

2002). This means not only ﬁguring out the answer to

a problem, but also describing the step-by-step pro-

cess that a machine (with no intelligence or common

sense) would be performing to obtain the answer. In

this scenario, there is much creativity, analysis and de-

sign skills in developing solutions, since there is usu-

ally a large body of acceptable solutions.

Algorithmic problem-solving thinking is at the

foundation of rational thinking in our civilization.

Greek thinkers where particularly interested in con-

structive methods as illustrated by Euclid’s elements.

We argue here that such approach can be regarded as

concrete programming. It offered a few basic oper-

ations (usually to draw a circle with a compass and

to draw a straight line with a ruler). Propositions

and their proofs were algorithms and proofs of cor-

rectness for such algorithms (Toussaint, 1993a; Tous-

saint, 1993b). The model of computation had a phys-

ical analogue and it was possible to experiment with

Estivill-Castro V. and Bartlett B..

IMAGE CAPTURE FOR CONCRETE PROGRAMMING - Building Schemata for Problem Solving.

DOI: 10.5220/0003314100560068

In Proceedings of the 3rd International Conference on Computer Supported Education (CSEDU-2011), pages 56-68

ISBN: 978-989-8425-49-2

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

a compass and a ruler on an instance of the problem.

We suggest that this approach should be used to

introduce students to programming. Our approach

is in contrast to the tradition to link closely the in-

struction on problem solving to instruction in syntax

and semantics of programming languages (Schneider,

1982; Koffman, 1988; Etter and Ingber, 1999; Sav-

itch, 2009). We question and seek an earlier con-

nection between problem solving and computer pro-

gramming. We propose to move gradually from con-

crete personal experiences to symbolic textual (ab-

stract) programming. We propose that the technology

is already there for capturing (in images and video)

the concrete constructions by the students, and that

such constructions should represent behaviour.

We aim for student involvement in action and aim

for better outcomes of ﬁrst year IT students. The

prompt for this improvement will be a program of

staged activities through which students build their

skills and agency in problem solving at both a meta-

level and for speciﬁc skills they will need in the

ﬁrst year course-work. We describe one develop-

mental activity with an emphasis on concrete oper-

ations moving through to an informed and abstracted

familiarity. We aim to strengthen students’ building

schemata by associating their action with appropriate

language for its labelling and discussion.

Problem-solving skills are more important than

learning several programming languages, because the

technologies to program computers vary constantly

- computers are faster and with more memory, but

they remain fundamentally state-transition machines.

Thus, learning a particular programming language is

ephemeral; describing solutions to problems algorith-

mically is and will continue to be an endurable skill.

However, learning the problem-solving skills neces-

sary for programming has proven to be hard, and so

has teaching them (Adams and Turner, 2008). It re-

quires signiﬁcant conceptual and abstract thinking,

regularly associated with the skills for solving mathe-

matical problems (Polya, 1957). However, for IT stu-

dents, there are additional challenges.

First Challenge: the generation of an algorithm

that works for all instances of the problem. Is-

sues are complicated because is impossible to per-

ceive with our senses what goes on on a computer

(let alone through entities like the Internet and the

Word Wide Web). A large literature on teach-

ing problem solving and a discussion on analyt-

ical skills in physics, mathematics and engineer-

ing is presented by James E. Stice at University

of Texas

mostly deriving from the pioneering

wwwcsi.unian.it/educa/problemsolving/stice ps.html

work of Donald R. Woods (Woods et al., 1975).

Other literature and its references cover many as-

pects of teaching problem solving (Adams et al.,

2007; Prince and Hoyt, 2002). For IT, teaching

and learning problem solving has the added com-

plexity of explaining and coding the solution in a

programming language.

Second Challenge: the abstraction of the descrip-

tion; namely, the language in which the solution is

expressed is an abstraction of the changes of state

that occur in abstractly described objects. The

complications of programming computers have

resulted in the software crisis. Producing software

is extremely difﬁcult, and usually does not meet

user expectations, it is faulty and needs upgrades.

The price of more powerful hardware drops while

inferior software remains costly. New software

developing tools are more sophisticated and pow-

erful. But such advances require more concepts,

from structured programming, to object-oriented

and recently to agent programming, for example.

Moreover, with each of these advancements, the

teaching of problem solving competes with the

need to train the IT-students in sophisticated en-

vironments as well as the need to introduce them

to a large body of concepts. As a result, some

students perceive fundamental concepts as unre-

lated and even irrelevant. However, the relevant

knowledge and common thread is indeed problem

solving and techniques to obtain algorithms.

2 THE STRATEGY

Our ﬁrst element is to develop learning activities per-

formed by students in teams. These activities must

be performed outside computer labs and must pro-

duce concrete constructions. Participants collaborate

in teams, around their constructions and not in the dif-

ﬁcult setting of sharing one monitor or a keyboard.

We remove the arrangement of participants facing in

one direction, to participants in collaborative arrange-

ments surrounding a construction that is captured and

interpreted by digital media. Then the software in

computer vision and image analysis is used to convert

the construction into meaningful behaviour in an au-

tomaton. Activities

relate to knowledge introduced

in at least 6 but possibly all 8 ﬁrst-year courses of

the Bachelor of IT. While such knowledge is not a

prerequisite, the activities introduce it, reinforce it, or

illustrate it by providing additional context. The ac-

tivities integrate concepts so students can establish re-

Activities are independent, but thematically linked.

IMAGE CAPTURE FOR CONCRETE PROGRAMMING - Building Schemata for Problem Solving

GLOBAL STEPS:

1. UNDERSTAND THE PROBLEM

2. DEVISE A PLAN

3. CARRY OUT THE PLAN

4. LOOK BACK AND REFLECT

1. Examine the solution obtained.

2. Can you check the result? Can you check

the argument?

3. Can you derive the solution differently?

Can you see it at a glance?

4. Can you use the result, or the method, for

some other problem?

Figure 1: Basic/classical approach to problem solving.

lationships between courses. For example, activities

on graph algorithms will incorporate concepts like ac-

cumulators, counters and absolute addressing from

1007ICT Introduction to Computer Systems and Net-

works but also notions like graphs from 1002ICT Dis-

crete Structures 1. Activities whose foundations are

state-automata, logic gates and Turing machines will

be linking with 1004ICT Foundations of Comput-

ing and Communication and 1007ICT again. Com-

plexity of software development and problem solv-

ing will take from 1410ICT Introduction to Infor-

mation Systems and 1420ICT Systems Analysis and

Design. Problem solving for programming is taken

from 1001ICT Programming 1 and 1005ICT Pro-

gramming 2. Activities will also be monitored across

vertical paths of the program.

The second element of the strategy is that activ-

ities can be extra curricular and students participate

in them by invitation and voluntary. Activities can be

presented within the framework of a competition (in

a similar fashion to the Science an Engineering Chal-

lenge) with interesting prizes (for added motivation).

Activities can also be adopted by course conveners.

For example, some of the activities may become re-

quired assessment in some of the courses mentioned

earlier; however, this would be if adopted by lecturers

or conveners of some of the courses.

Educational theories like Constructive Align-

ment (Biggs, 1999) suggest students should be

aware that the learning outcomes are problem-

solving skills and we will follow this sugges-

tion. Therefore, the next element of the strat-

egy is a guide on Teaching Problem Solving

based on the theory from technical ﬁelds like

engineering and mathematics (Wickelgren, 1995;

Houghton, 2004) (and the Higher education Academy

Engineering Subject Center on Problem Solv-

ing [www.engsc.ac.uk/er/theory/problemsolving.asp]

Figure 2: The basic operations.

and its corresponding supporting educational theo-

ries (Houghton, 2004)) but adapted to information

technology and problem solving for algorithm devel-

opment. We will use Constructive Alignment (Biggs,

1999) in order to ensure our assessment methods and

our learning activities achieve the intended learning

outcomes; namely improved problem-solving skills.

Our intention is to evaluate under the following def-

inition “Problem solving is the process of obtaining

a satisfactory solution to a novel problem, or at least

a problem which the problem solver has not seen be-

fore” (Woods et al., 1975). We may extend this to

problem solving for software development and sys-

tems architecture.

A fundamental difﬁculty in teaching ICT at Grif-

ﬁth University is the limited ability of a substan-

tial percentage of the student cohort to think in

abstract terms (we explained before the low OP

scores achieved by students enrolling in the pro-

grams (Estivill-Castro, 2010)). This restricts the stu-

dent’s ability to solve problems, as well as their ability

to recognize the potential of applying already known

knowledge in unfamiliar new situations (which, if de-

scribed in abstract terms, proves to be the same or

similar to an already known problem). The planned

teaching / learning methodology we apply has some

distinct characteristics:

• In the activities, students are presented with con-

crete problems and participate in solving them.

But the activities engage students with different

levels of abstract thinking ability to successfully

participate.

• Through a series of increasingly difﬁcult exercises

involving guidance (cf. Social Constructivism),

answering ’what if’ (Brown and Walter, 1990;

Brown and Walter, 1970) questions. With inde-

CSEDU 2011 - 3rd International Conference on Computer Supported Education

pendent discovery, students construct and reﬂec-

tively explain a generic solution, which leads to

an implementation / algorithm — this approach

not only ensures to test whether students managed

to constructed their own understanding, but also

develops their abstraction skills.

• Exercises exploring the limits of the solution

(through comparing the problem to other similar

ones and through asking ’what if not’ questions)

will help the learner to develop skills to recognize

concrete situations in which known abstract solu-

tions apply.

The constructive approach and the use of teach-

back (Pask, 1975; Vygotsky, 1978), ensure that the

understanding of the problem and the understand-

ing of the solution become an observable occasion.

Our design of activities (to be performed by teams

of students) is around a series of puzzles for re-

alistic problems. In these problems, the students

will construct a solution, but instead of initially us-

ing a keyboard/computer (and a formal program-

ming language as in traditional text-based program-

ming), they will commence by constructing physi-

cal artefacts. We refer to this as concrete program-

ming although it has similarities with puzzle-based

learning (Michalewicz and Michalewicz, 2008) and

with problem-based learning (Cindy E. Hmelo-Silver

et al., 2007, and references). We demonstrate here

that high-school students can participate in the activ-

ities including some instruction in textual program-

ming.

Our approach is to use concrete physical objects to

build ﬁrst phase solutions: here, the students will have

playing cards, or other physical components (like

LEGO or Konex) and they will build concrete phys-

ical solutions (but still descriptions of algorithms) to

small instances of the puzzles. The students will be

asked to attempt to obtain algorithms that work in

general. However, these algorithms may fail in some

of the many conﬁgurations. These will incorporate

elements of role-play in learning. The second compo-

nent of our approach is to use automated assessment:

we propose to use a digital camera to capture the con-

structions (algorithms) of the students, and develop

image processing software to interpret their physical

programs; then execute them (run them) with all pos-

sible inputs and award them a score relative to the

fraction of inputs in which they are correct. The third

phase of our approach is programming by simulation.

The approach is close to visual programming, but

tackling larger problems than with the physical ma-

nipulation of ‘LEGO-brick’ or ‘playing cards’. How-

ever, we developed complementary educational soft-

ware that emulates the puzzles and the concrete pro-

gramming languages. Participants use simulations of

cards, and tiles, and compose programs in the same

way as in the physical world, but all in a Graphi-

cal User Interface (GUI). For example, RoboLab by

LEGO illustrates visual programming and is used by

teenagers and university students to program Mind-

Storm Robots. The fourth stage is the transition

to textual programs. To this end we will use envi-

ronments oriented for the puzzle in the educational

programming language

MaSH

(developed by Dr. A.

Rock).

MaSH

is an imperative subset of the program-

ming language Java (and by removing many of the

sophistication of Java, ﬁrst-year students understand

every line of code they use).

Students are provided with guidance and in-

struction for problem solving (Jones, 1998). We

started with classical approaches. An extreme

summary (Polya, 1957, www.math.utah.edu/˜

pa/math/polya) has been provided for high-school

trials, see Fig. 1. Later, more elaborate instruction

on problem solving will be provided. For example,

students may be provided with more details on one

of the step in Fig. 1. In general, much more sophis-

tication on problem solving will be delivered than

can be illustrated here; at each step elaborating on

the techniques for problem solving and in particular,

for algorithm analysis and design (Skiena, 2008). As

alluded to before, activities illustrate a wide range

of useful problem-solving skills: analogy, simpli-

ﬁcation, exploration, iteration, divide and conquer,

and recursion. Instruction, illustrations and materials

on methods like divide-and-conquer, reduction, and

analogy will be formally provided.

3 ILLUSTRATION

The activity we use as an example is named “sort-

ing cows” but is based on Sorting Networks (Knuth,

1973, Section 5.3.4) and has similarities with the

Sorting Networks activity popularised by “Com-

puter Science Unplugged” (csunplugged.org/sorting-

networks). In its ﬁrst stage, the participants are intro-

duced to the basic operations of sorting bridges (also

named gates). The analogy is a series of rails popu-

lated by cows that are connected by the gates. The

gates may swap cows across rails, and the generic

goal is to design and arrangement of the gates that

achieves a certain objective, for example, placing the

largest cow in the ﬁrst rail. These simple operations

are comparison operations and swap operations. The

Blue (also named large up) operations ensure that the

larger cow is in the lower numbered rail when two

cows (items) meet at it. The green gate (also named

IMAGE CAPTURE FOR CONCRETE PROGRAMMING - Building Schemata for Problem Solving

Figure 3: High-schools students constructing sorting networks and experimenting in their own person the effect of their

construction.

larger down) always places the largercow in the larger

numbered rail. The red gate always swaps the cows.

3.1 First Stage — Concrete & Personal

In the ﬁrst stage of the activity, the experience is phys-

ical and personal. The participants walk on carpet that

represent the rails and experience themselves the fact

that they must wait at a gate for another participant

in the connected rail, and then perform the required

operation as per color (function) of the gate. They ex-

perience conﬁgurations for 3 or 4 participants and try

to discover permutations which fail to reach the ob-

jective. For example, the network does not sort. They

also may be asked to explore some patterns and to

discuss the parameters of the problem. Instruction of

problem solving is given by analysing ﬁrst what prob-

lems may be feasible and which may be not. Varia-

tions like ﬁnding the largest and the smallest without

sorting, or using only one type of gates are discussed

as well as considering that the cost of bridges/gates

may not be always uniform when rails are further

apart. Fig. 3 shows high-school students construct-

ing networks and personally navigating them. The

images correspond to two Grifﬁth University Expe-

rience Days (19th of May and 27th of July 2010), and

3 days (21st, 22nd and 23rd of July 2010) of the Sci-

ence and Engineering Challenge.

This is what we describe as a concrete experi-

ence that is based on Piagetism and will be moved

to a more informed and abstract familiarity. The idea

is to strengthen the students’ semantic schemata (or

their building processes) by associating their experi-

ence and their action with appropriate language. We

expect that such language will include words like sort-

ing, comparison, swap, cost, algorithm, permutation,

and the like. It also will have more possibilities for

abstractions like the notion of sorting network itself.

Moreover, some inquiry questions that put in prac-

tice mathematical problem solving can also be inves-

tigated at this stage (participants should be able to ar-

gue that in order to sort or to ﬁnd the largest cow, all

rails must connect with at least one gate).

3.2 Second Stage — Concrete

Constructions

In the second stage of the activity, the participants still

work away from computers and continue using con-

crete objects. In this case, they build with cloth and

corresponding strings artefacts that represent the net-

works. They lay the rails and the bridges and exper-

iment, evaluate and interact their concrete construc-

tions. Fig. 4 shows the types of networks that can be

physically built with a white blanket as background,

black stripes as rails, and also cloth strings as gates.

We emphasize that the experience remains con-

crete. The participants are using tangible rails and

gates. However, they are able to build larger networks

and discuss larger instances. The intention is to initi-

ate the exploration of patterns that may scale to larger

solutions. These networks will cause behaviour. We

achievethis by capturing them with a camera and exe-

cuting them in a simulator. The participants construct

concrete artefacts that encode behaviour. This is what

we name concrete programming.

The realization that this network is a represen-

tation of computation (that is, an encoding of be-

CSEDU 2011 - 3rd International Conference on Computer Supported Education

Figure 4: A sorting network constructed of cloth and capturing the network into the virtual environment.

Figure 5: Teams of students working on constructing solutions for selection and sorting problems on networks.

haviour) is achieved by our supporting tools. These

networks are captured by a camera (as simple as a

mobile phone camera) and fed trough an image recog-

nition software. This image recognition software re-

cuperates the network and can represent it in a graph-

ical user interface that is also coupled with a simu-

lator. The participants can see the effects of the net-

work in any permutation they wish to test it, or on a

sample test set or even more in all permutations (as

long as the network has less that 9 rails). A partici-

pants network can be evaluated against many objec-

tives. The user can chose the objective (like ﬁnding

the median). They also get feedback on the cost of the

network in parameters like gates used, or time used.

With this, participants are converting their construc-

tions to a graphical simulation in the computer and

observing the effect on their tests.

3.3 Third Stage — Virtual

Constructions

Once this step is completed, the participants can move

completely to the graphical user interface and conﬁg-

ure far larger networks that would be possible phys-

ically, and explore far more patterns. For this, our

earlier software tool allows to interactively add and

manipulate all the elements previously experimented

physically. Here, participants still manipulate gates,

and rails, but on a virtual environment provided by

the GUI-enabled tools.

This is the third stage: the experience remains

concrete. However, such experience is no longer

physical, but is nowan immersion into a virtual world.

All the actions of the sorting network, and the rails,

and the cows belong now in the environment of the

simulator and the graphical user interface. The tool

provides feedback. It can be tested on speciﬁc in-

stances, or on all permutations of 9 or less items. It

can sample a large number of permutations for larger

instances and also provide feedback on different cri-

teria and cost functions. For example gates that join

adjacent rails may be less costly than those that join

rails far apart.

Participants can address even larger instance;

however, large networks become impossible to build

for a particular objective unless one identiﬁes a pat-

tern. The identiﬁcation of these patterns introduces

notions like subproblem. A clear example of this pat-

tern is a common solution to ﬁnding the smallest cow

and placing it at the bottom rail (see Fig. 6) This pat-

tern enables analysing if the number of blue gates

used is optimal for any number of rails. More inter-

estingly, it enables to discuss other aspects of the pat-

tern. If all the gates are replaced by red gates, then the

IMAGE CAPTURE FOR CONCRETE PROGRAMMING - Building Schemata for Problem Solving

Figure 6: Placing the smallest cow in the bottom rail.

pattern corresponds to a cyclic shift, where each cow

moves to the next rail up, except of course the cow on

the ﬁrst rail. The one on the top rail “wraps-up” and

appears in the bottom rail.

For example, from repeatedly ﬁnding the largest

cow with a diagonal pattern, it is possible to scale the

pattern down from n rails to n − 1 rails. The pattern

can also be seen as scaling up the basic operator from

2 to 3 rails. However, this pattern can be repeated to

create a sorting network by using it repeatedly from

size n, then n− 1 and so on down to 2.

At this stage is also possible to introduce more

language. We illustrate the fact that ﬁnding the largest

item can be used repeatedly for sorting. Moreover,

one can discuss many of the sorting networks in the

literature and discuss algorithmic strategies. In par-

ticular, is possible to introduce algorithmic problem-

solving terminology like recursion and divide and

conquer without the presentation syntax and seman-

tics of a textual programming language.

We argue that even more important technical con-

cepts can be built. This is what we mean by given

the students schemata with strong understanding and

meaningful semantics. It is possible to illustrate and

argue about the correctness and optimality of the con-

structions. One can even motivate and introduce the

mathematical notion of proof by induction and con-

nect it (Wand, 1980) to the algorithmic strategies.

3.4 Fourth Stage — Textual

Constructions

From here, the 4-th stage of the activity is the

migration to a textual encoding of this behaviour.

We introduce this using a particular environment of

MaSH

(Rock, 2010).

MaSH

stands for “Making Stuff

Happen” and it is a tool to create textual programming

Rewrites

void main()

Purpose: A program that is organised into methods must have

a main method (a procedure with no arguments). This will be the

first method to execute. **** automatically rewrites this method

to conform to standard Java.

Methods

void createRails(int size)

Purpose: Create a random permutation of size size. There is a

limit of 100 rails.

void redSwap(int i, int j)

Purpose: Always swap the items in the i-th and j-th position.

void blueLargerUp(int i, int j)

Purpose: If i < j place the larger in the i-th position and

the smaller in the j-th position.

void greenLargerDown(int i, int j)

Purpose: If i < j place the larger in the j-th position and

the smaller in the i-th position.

void printOrder()

Purpose: Display the order of items in the network.

Figure 7: The API of the

MaSH

environment

sortingnetwork

environments where syntax and semantics are sim-

ple. We have constructed one of those environments

called sortingnetwork whose documentation appears

in Fig. 7. This environment is an API that emu-

lates completely the GUI but enables the introduc-

tion of textual programming language concepts. We

start with the level named statements in

MaSH

and can

produce a direct mapping between the visual repre-

sentation of sorting networks in the GUI and

MaSH

statement program. For example, the

MaSH

-statement

program in Fig. 8(a) corresponds to a sorting net-

work that has only one gate between two adjacent

rails and always swaps the items. The program can

be the result of exporting a sorting network built in

the virtual environment. It can also be constructed

with a text editor (an imported to the tool for visu-

alization). This enables the introduction of concept

like “identiﬁer”, “separator”, and most of the lexical

instruments experienced in textual programming lan-

guages. Other concepts at the level of statements that

the participants can practice and understand are “se-

quential control”, “comments”, “displaying output”

and “method/function invocation”. The simple

MaSH

program of Fig. 8 is randomised. Each execution gen-

erates the values randomly and its output may be as in

Fig. 8(b) or as in Fig. 8(c).

There are several sub-levels in this stage of the ac-

tivity that correspond to the levels in the design of

MaSH

but which can be reinforced with the activity.

The repetition of the comparator each time in the next

rail for all rails results directly into a control structure.

That is, we can introduce the notion of a “for-loop”.

Fig. 9 presents the program where red gates are used

to cyclically shift. This program was sufﬁcient for us

CSEDU 2011 - 3rd International Conference on Computer Supported Education

import sortingNetwork;

createRails(2); // create two rails

// with data in random order

printOrder(); // print the data

redSwap(0,1); // Swap values in the rails

printOrder(); // print the data

(a) Simple

MaSH

program at level statements.

90, 32,

32, 90,

(b) Sample output 1.

13, 26,

26, 13,

Figure 8: Simple

MaSH

program and sample output.

import sortingNetwork;

createRails(5); // create five rails

// with data in random order

printOrder(); // print the data

// cyclically shift one position to the left

for (int i=0; i<4; i=i+1)

redSwap(i,i+1);

printOrder(); // print the data

(a) “For-loop’ in a

MaSH

program at level control structures.

12, 54, 9, 3, 4,

54, 9, 3, 4, 12,

(b) Sample output 1.

78, 3, 18, 63, 13,

3, 18, 63, 13, 78,

Figure 9:

MaSH

program to introduce control structures.

to introduce control structure concepts to high school

students with no programming experience. We could

illustrate and have even meaningful discussion about

the limit used in the for-loop for the index variable

That is, the program has

i<4

as the termination con-

dition but the data consists of 5 elements. Signiﬁcant

discussion is generated then about the actual parame-

ters to

redSwap

in the body of the control structure.

Another aspect that can now be introduced builds

on the discussion of patterns from the previous con-

crete experience. The pattern we described earlier

where using a solution to place the smallest as a sub-

problem to sorting, enables the introduction of the no-

tions of method (or subroutine). For example, we can

encode the pattern into a subroutine ﬁrst. This is il-

lustrated by a

MaSH

program that corresponds to two

invocations of ﬁnding the smallest which corresponds

to a network to place the two smallest cows in the

bottom two rails. The

MaSH

program corresponding

to Fig. 10 is presented in Fig. 11. This enables the in-

troduction of concepts like formal parameters and the

control-ﬂow generated by this function invocation.

Similarly we can discuss concepts like side-effects al-

though fundamentally all variables are global at this

level and there is no data encapsulation. However, the

Figure 10: A network that extracts ﬁrst and second by two

applications of the diagonal pattern.

import sortingNetwork;

void select (int place) {

for (int i=0; i<place; i=i+1)

blueLargerUp(i,i+1);

}

void main() {

createRails(5); // create five rails

// with data in random order

printOrder(); // print the data

select(4); // Select with 4 comparisons

select(3);

printOrder(); // print the data

}

Figure 11:

MaSH

program using subroutines in the Sorting

networks environment.

important aspect is we have a concrete experience to

ground the discussion of the abstract elements of tex-

tual programming languages. It is important to realize

that control structures in the

MaSH

programming envi-

ronment become generic in terms of the size of the

instance. This is not possible with the concrete sort-

ing networks, which are built for a speciﬁc size. This

is another point that the participants should observe.

It also allows expanding the discussion regarding the

generality of a solution in problem solving. The re-

duction of a problem to another problem for which we

already know a solution is a problem-solving strategy

that is ubiquitous in algorithm design. We can visual-

ize the repetition of the selection of a smallest element

in a sorting network, refer to Fig. 12. The

MaSH

pro-

gram of Fig. 11 can be generalised to a sorting pro-

gram as per Fig. 13. The activity can now progress

more rapidly into other programming concepts and

in particular,

MaSH

is designed to introduce behaviour

ﬁrst and later introduce data, and ﬁnally introduce the

plethora of object-oriented concepts.

IMAGE CAPTURE FOR CONCRETE PROGRAMMING - Building Schemata for Problem Solving

Figure 12: A sorting network.

3.5 Stage Five — Advanced Topics

and Research

We envisage also a later stages of these activities,

that can lead to artiﬁcial intelligence (like to search

for cost optimal networks for speciﬁc parameters of

the problem), or even to research challenges, like to

establish the best network for certain cost structures

and sets of operators. The activity also leads itself

to consider concurrency and parallelism and the in-

troduction of programming concepts in this area. In

particular, the tools has been used in ICT2501 Pro-

gramming 3 to illustrate the algorithmic complexity

of selection sort. The tool provides a visual tangi-

ble (concrete) illustration that selection sort requires

O(n

) comparisons, since the sorting network uses

gates in all positions on one half of a grid of width

n and thus, of area n

4 THE EXPERIENCE

We have performed these two activities with 14

groups of participants from high-schools as part of the

events mentioned earlier (a total of 56 students organ-

ised in groups and additionally 8 students as individu-

als). These were conducted as trials for the activities.

Each activity was conducted at least once by a person

who was not the designer of the activity, who is not

an academic and not trained as an instructor but who

had witnessed the activity once. There were no major

differences in the execution of the activity and all oth-

ers who were conducted by Estivill-Castro (one day

with assistance of Dr. S. Venema). Our intention was

to evaluate the following aspects.

1. Do the participants acquire technical language

and have a have better semantic understanding for

the concepts of such language?

2. Do the participants acquire and understanding

that problem-solving is a strategic and acquired

skill?

3. Does the concrete experience assist in problem-

solving?

4. Is the organization in teams useful?

4.1 Semantic Understanding of

Language

The ﬁrst research issue was evaluated by a short in-

terview before the activity and a questionnaire after

the activity. The interview assessed the previous un-

derstanding of some terminology while the question-

naire investigatedthe understanding of activity related

technical concepts and the use of new terminology.

The results were promising. For example, prior to the

activity, very few of the students could enunciate a

clear deﬁnition of the notion of median and even less

clear was any connection with the notion of mean.

However, by the end of the activity, the notion of

median was clearly described by the participants and

they could make the observation themselves that it is

not uniquely deﬁned when there is an even number

of items. Some participants were capable of realizing

that the median is a robust estimator of the central ten-

dency and that enlarging the largest item or reducing

the smaller element does not affect the value of the

median (however, such changes in the data do affect

the mean).

There was a similar visible extension on the under-

standing of terms like algorithm, problem, instance of

a problem, veriﬁcation, and correctness. Many other

concepts were not formally evaluated by the question-

naires but it was clear the participants gained insight.

For example, they understood that testing all permuta-

tion to verify correctness of a sorting network grows

very rapidly with the number of rails (items). Simi-

larly, some realised that verifying the network is the

most economical (by a criteria like least number of

gates) was even more unfeasible to verify by exhaus-

tive exploration. Other terminology like cyclic shift,

coding and programming language also showed im-

provements.

In fact, some students were able to make very in-

sightful observations. That is, to enunciate a claim

and then provide and argument for justifying its

validly. This emulated the formulation of a theorem

and its proof although not structured in this way. An

example of this happening is “In a network with only

blue gates, the smallest element never ﬁnishes in a rail

above to where it started”. We ﬁnd interesting that

from this, the team of participants where it emerged

was able to rapidly generalize how to ﬁnd the largest

item, and/or the smallest, and then discover patterns

and build a sorting network that would solve prob-

lems for all sizes. They were also able to structure ar-

CSEDU 2011 - 3rd International Conference on Computer Supported Education

import sortingNetwork;

void select (int place) {

for (int i=0; i<place; i=i+1)

blueLargerUp(i,i+1);

}

void sort (int place) {

for (int i=place; i>0; i=i-1)

select(place);

}

void main() {

createRails(5); // create five rails

// with data in random order

printOrder(); // print the data

sort(4); // Sort

printOrder(); // print the data

}

Figure 13:

MaSH

program using subroutines for sorting.

guments for the correctness of their approach. More-

over, they could then formulate other claims about the

need for red or green gates in order to place the small-

est element above the rail it starts (in particular, they

could made the observation about the impossibility of

sorting in descending order only with blue gates).

4.2 Strategies for Problem Solving

For this we also had a questionnaire after the activ-

ity asking if the information on problem solving was

useful (information along the lines of Fig. 1 in one

A4 page was distributed to participants). We also had

one control group to whom no instruction on problem

solving was provided neither any material on problem

solving .

In this case the informal observations we per-

formed offered some contradictory observations.

Some participants did not seem to be able to attack

the problems in any way, particularly those that were

not in groups. Some high-school students seemed

preoccupied with there being an answer they should

havepreviousknowledge for and seem to see the chal-

lenges of the activities as test on their memory. How-

ever, the vast majority engaged in the activity, partic-

ularly as we mentioned, when grouped in teams.

The positive outcomes in this regard were many.

For example, some participants were able to apply ef-

fectively strategies like “start with a smaller problem”

and they used the solution from ﬁnding the largest

item to ﬁnd a network to sort. Several could indeed

examine the solution they obtained and generalize

it. Some were able to reﬂect on the problem state-

ment and discuss their understanding of the challenge.

They could be systematic and eliminate possibilities

or consider all cases. They could understand what a

counter-example means.

We also found some very genuine ideas. For ex-

ample, we found that two groups actually found a very

interesting and to our knowledge innovative approach

to construct a sorting network. Because the ﬁrst prob-

lem provided to them in the ﬁrst phase is to ﬁnd the

smallest item on 3 rails, teams commonly produced a

diagonal optimal pattern like in Fig. 6. (see bottom

right image on Fig. 3). The next problem was to ﬁnd

the maximum. For this problem, some teams used

the previous idea but now the diagonal pattern follows

placing the next blue gate on the winner and runs sym-

metrically in the other direction (see Fig. 14(a)). It is

not hard to compose these two patterns to identify the

smallest and the largest items in a network with four

rails (see Fig. 14(b) and Fig. 14(c)). When the stu-

dents attempted to sort on a network of 4 rails they

realised that they only need to ensure the two rails in

the middle work. This produces the sorting network

shown in Fig. 14(d) and visible in the images on the

bottom left of Fig. 3. This network is extremely ef-

ﬁcient for sorting 4 rails, requiring only 3 time steps

(better than the pyramid pattern in Fig. 12). What we

found extremely interesting is that when this approach

is generalised to 8 rails in the constructions with tape,

some of the teams produce the network that reduces

the problem of sorting n rails to sorting the n−2 mid-

dle rails and produce a network like in Fig 14(e). Be-

sides a visually appealing pattern, this network has

some interesting properties, it uses only blue gates

besides adjacent rails (no long gates) and it uses the

same number as the corresponding pyramid pattern of

Fig. 12. While it requires more parallel time units, it

does have some degree of parallelism.

Although we have no space here to describe the

Dinosaur activity sufﬁce to say it consists of describ-

ing heuristic algorithms for the NP-Complete prob-

lem VERTEX COVER

. Participants spontaneously

produced randomised heuristics, algorithms based on

local search (selecting all vertices and then removing

unnecessary vertices from the cover plus local pertur-

bations), algorithms based on structure ﬁnding (ver-

tices of degree one, or triangles — cycles of length 3)

and greedy algorithms (choosing a vertex of largest

degree). The notion of a competitive algorithm did

not emerge as this seems an advanced concept.

4.3 Usefulness of the Concrete

Experience

We were interested in investigating if the ﬁrst stage

of the activity (the concrete experience on the partici-

pant) has a positive impact. Thus, we reserved 8 par-

To cover edges by selecting the minimum number of vertices

in a graph. An edge is covered if at least one of its endpoints is in

the selected cover.

IMAGE CAPTURE FOR CONCRETE PROGRAMMING - Building Schemata for Problem Solving

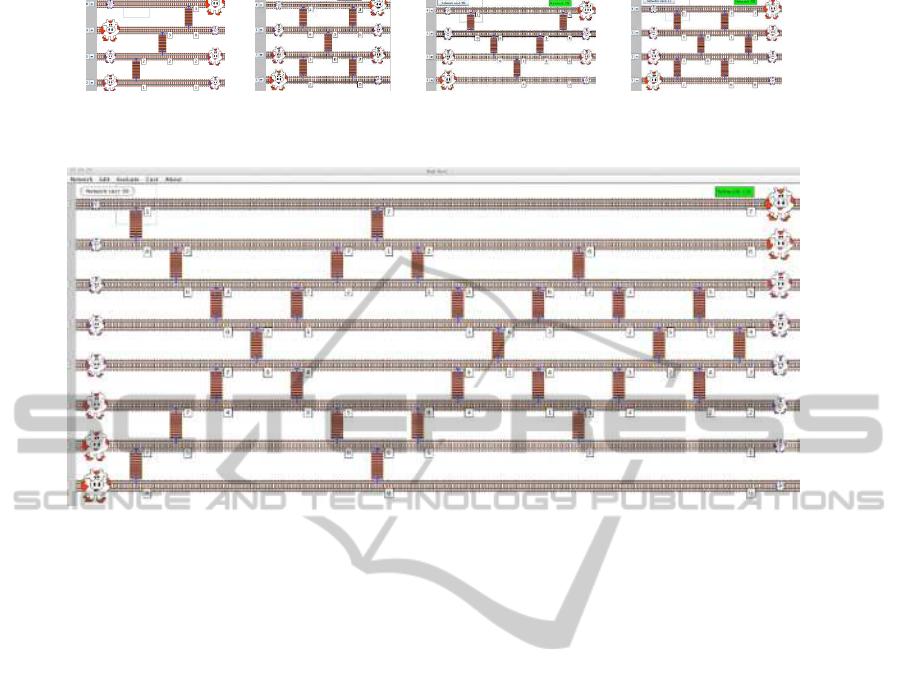
(a) Largest of 4 rails. (b) Optimal

parallel

pattern to ﬁnd largest and

smallest item in for rails.

pattern to ﬁnd

largest and smallest.

(d) A gatein the middle rails

sorts.

(e) Sorting network from recursive application of

pattern.

Figure 14: A very symmetrical sorting network by a recursion that ﬁnds simultaneously the largest and the smallest item.

ticipants who were not involved in the ﬁrst phase an

their involvement commenced with the second phase

where the construction is concrete but not personal.

We used two measures to evaluate the difference be-

tween these 8 participants and the others. First, we

measured the number of times they required further

assistance or clariﬁcation by the person conducting

the activity. Second, we measured the time it took

for them to complete activities of the second phase as

well as the time it took them to complete problems

using the virtual rails tool (stage 3).

The second measure was the number of times

there was a request for assistance or clariﬁcation from

the activity conductor or the assistant. While the data

may have a signiﬁcant margin of error in measure-

ment it does reﬂect that high-school students that par-

ticipated in a physical phase of the activity where each

person had to role-play a cow (or a dinosaur) even-

tually was getting better at facing the new problems

and the new challenges. Those that skip the role-play

phase save the time of this part and thus, complete

the challenges of the concrete part (phase 2) perhaps

sooner or at least not worse than those that did the

role-playing. However, these second group of partici-

pants struggle with the later challenges and activities.

For example, we proposed to ﬁnd the median element

and place it in a speciﬁc position using the virtual tool

on a network of 9 rails, very few of the participants

without the role-playing could complete this activity.

assistant(s). Fig. 15 shows the comparisons in phase

2 challenges (build a network to ﬁnd the maximum,

ﬁnd a network to ﬁnd the minimum, ﬁnd a network

that sorts) and one challenge from phase 3 (place the

largest on the top rail and the smallest in the second

rail). The data reﬂects the trend that individual work

is not as effective as during the different activities the

average number of queries remains above 1 per stu-

dent, suggesting is more efﬁcient to group the partic-

ipants in teams as this seems they assist each other.

4.4 Organization in Teams

We measure the same two aspects of participants in

teams and compared against 8 participants that were

not placed in teams. The data reﬂects that teams

progress better with the later challenges than those

that work in isolation. However, we are not sure that

everyone in the team reaches the same command of

the concepts and ideas.

Team-work proved to be productive and we can

feel conﬁdent that the teams progress well. One in-

teresting aspect is that we were able to observe actual

collaboration and participation. It is usually difﬁcult

to see this type of interaction between members of

a team in traditional laboratories for delivering pro-

gramming concepts or problem solving concepts. In

CSEDU 2011 - 3rd International Conference on Computer Supported Education

Figure 15: Comparing students in groups, as individuals and groups without phase 1 in completing a network for 4 types of

progressively more advanced problems.

Figure 16: Teams of students working on constructing difﬁcult instances of vertex cover (cities) and then actual covers

(dinosaurs on vertices guarding edges).

particular, with current labs suited with workstations

ﬁtted for individual use it is very rare to see two stu-

dents collaborating and having meaningful discussion

with the physical limitation of one monitor. We can

see that we were able to produce constructive interac-

tions with all team members as can be seen in the im-

ages of Fig. 5 and Fig. 16. The images reveal several

situation in with a a hand from at least 3 participants,

if not all four in a team, actively engaging with the

concrete construction. This suggests complementing

teaching labs with interactive whiteboards or other

technologies where students could interact in groups

and collaborative edit and modify the current design

or solution. Thus, we see an earlier introduction to

Computer Supported Cooperative Work.

5 CONCLUSIONS

This paper present initial approaches to teach prob-

lem solving for programming as the construction of

physical artefacts (and not textual items). While vi-

sual programming enables concrete manipulation of

objects, the environment is still virtual. We propose

to commence with the personal and physical experi-

ence as a preliminary step and use technology to cap-

ture images and video of such constructs in order to

produce a behaviour in a system.

ACKNOWLEDGEMENTS

This work would not have been possible without the

programming talent and skill of Nathan Lovell PhD,

and the ﬁnancial support of a Teaching and Learning

Grant from Grifﬁth University.

REFERENCES

Adams, J., Kaczmarczyk, S., Picton, P., and Demian, P.

(2007). Improving problem solving and encouraging

creativity in engineering undergraduates. In Interna-

tional Conference on Engineering Education ICEE-

07, Coimbra, Portugal.

Adams, J. and Turner, S. (2008). Problem solving and cre-

ativity for undergraduate engineers: process or prod-

uct? Innovation, Good Practice and Research in En-

gineering Education, page 61.

Biggs, J. (1999). Teaching for Quality Learning at Univer-

sity. Shire and Open University Press, UK.

IMAGE CAPTURE FOR CONCRETE PROGRAMMING - Building Schemata for Problem Solving

Brown, S. and Walter, M. I. (1970). What if not? an elabora-

tion and second illustration. Mathematical Teaching,

51:9–17.

Brown, S. and Walter, M. I. (1990). The art of problem

posing. Lawrence Earlbaum, Hillsdale, NJ, second

edition.

Cindy E. Hmelo-Silver, C., Duncan, R. G., and Chinn, C. A.

(2007). Scaffolding and achievement in problem-

based and inquiry learning: A response to Kirschner,

Sweller, and Clark (2006). Educational Psychologist,

4(2):99–107.

Dale, N. and Weems, C. (2002). Programming and Problem

Solving with C++. Jones and Bartlett Publishers, Inc.,

USA, 3rd edition.

Dewar, J. M. (2006). Increasing maths majors’ success and

conﬁdence through problem solving and writing. In

Rosamond, F. and Copes, L., editors, The Inﬂuences

of Steven I, Brown, pages 117–121, Bloomington, In-

diana. Educational Transformations, AuthorHouse.

Estivill-Castro, V. (2010). Concrete programing for prob-

lem solving skills. In G´omez Chova, L., Mart´ı Be-

languer, D., and Candel Torres, I., editors, Interna-

tional Conference on Education and New Learning

Technologies (EDULEARN 2010), pages 4189–4197,

Barcelona, Spain. International Association of Tech-

nology, Education and Development (IATED). CD-

ROM ﬁle 454.pdf, ISBN: 978-84-613-9386-2.

Etter, D. M. and Ingber, J. (1999). Engineering Problem

Solving with C. Prentice-Hall, Inc., Englewood Cliffs,

NJ.

Houghton, W. (2004). Learning and Teaching Theory for

Engineering Academics. Engineering Subject Centre.

Jones, M. (1998). The Thinker’s Toolkit: 14 Powerful Tech-

niques for Problem Solving. Three Rivers Press, USA.

Knuth, D. (1973). The Art of Computer Programming,

Vol.3: Sorting and Searching. Addison-Wesley Pub-

lishing Co., Reading, MA.

Koffman, E. (1988). Problem Solving and Structured Pro-

gramming in Modula-2. Addison-Wesley Publishing

Co., Reading, MA.

Michalewicz, Z. and Michalewicz, M. (2008). Puzzle-

Based Learning — An Introduction to Critical Think-

ing, Mathematics, and Problem Solving. Hybrid Pub-

lishers Pty Ltd, Victoria, Australia.

Pask, G. (1975). Conversation, cognition and learning. El-

sevier, New York.

Polya, G. (1957). How to Solve It: A New Aspect of Math-

ematical Method. Princeton University Press, second

edition.

Prince, M. and Hoyt, B. (2002). Helping students make the

transition from novice to expert problem-solvers. In

32 Annual Frontiers in education (FIE-02), volume 3,

pages F2A7–11, Los Alamitos, CA, USA. IEEE Com-

puter Society.

Rock, A. (2010). Creating MaSH programming environ-

ments. School of ICT, Grifﬁth University.

Savitch, W. (2009). Problem Solving with C++. Addison-

Wesley Publishing Co., Reading, MA, 7th edition.

Schneider, M. (1982). An introduction to programming and

Problem Solving with Pascal. Addison-Wesley Pub-

lishing Co., Reading, MA, 4th edition.

Skiena, S. S. (2008). The Algorithm Design Manual.

Springer-Verlag, London, second edition.

Toussaint, G. (1993a). A new look at Euclid’s sec-

ond proposition. The Mathematical Intelligencer,

15(3):12–23.

Toussaint, G. (1993b). Un nuevo vistazo a la segunda

proposicion de Euclides. Mathesis, 9:265–294.

Vygotsky, L. S. (1978). Mind and society: The development

of higher psychological processes. Harvard University

Press, Cambridge, MA.

Wand, M. (1980). Induction, Recursion and Programming.

Elsevier Science Inc., New York, NY, USA.

Wickelgren, W. (1995). How to Solve Mathematical Prob-

lems. Dover, New York.

Woods, D., Wright, J., Hoffman, T., Swartman, R., and

Doig, I. (1975). Teaching problem-solving skills. En-

gineering Education, 66(3):238–243.

CSEDU 2011 - 3rd International Conference on Computer Supported Education