HAND GESTURE RECOGNITION THROUGH ON-LINE

SKELETONIZATION

Application of Continuous Skeleton to Real-time Shape Analysis

Alexey Kurakin

Moscow Institute of Physics and Technology, Moscow, Russian Federation

Leonid Mestetskiy

Moscow State University, Moscow, Russian Federation

Keywords:

Continuous skeleton, Shape analysis, Feature extraction, Gesture recognition, Hand tracking, Computer vi-

sion.

Abstract:

New method for palm shape analysis and hand gesture recognition with help of continuous skeletons is pre-

sented in the paper. Continuous skeleton makes possible to develop fast and simple methods for palm shape

analysis and measure a lot of its features. In particular it is possible to develop efﬁcient methods for segmenta-

tion and analysis of the object topological structure, measuring relative location of object parts and measuring

width of the object in arbitrary place. Applying to palm shape analysis skeleton provides a way to determine

number of visible ﬁngers, estimate their thickness and location, and perform efﬁcient palm shape comparison

with the sample. Moreover proposed approach allows measuring all mentioned features regardless of palm

orientation in the frame. And efﬁcient algorithms for skeleton construction allow performing shape analysis

with high speed in real-time applications.

1 INTRODUCTION

At the present time gesture recognition problem is

subjected to active research due to its practical im-

portance. Potential applications of gesture recogni-

tion technologies include human-computer interac-

tion (Dhawale et al., 2006), virtual reality applica-

tions (Aguiar et al., 2009), sign language recognition

(Burger et al., 2007) and other (Mitra and Acharya,

2007; Garg et al., 2009).

A lot of different approaches for hand gesture

recognition exist. Some of these methods require sev-

eral cameras or special equipment (Schlattman and

Klein, 2007; Wang and Popovi´c, 2009). There are

methods which maximize the likelihood of hand to

be in certain pose by input image (Liu et al., 2008),

but such methods are computationally expensive. An-

other group of methods work in real-time without spe-

cial equipment (Burger et al., 2007; Dhawale et al.,

2006). However, the range of possible conﬁgurations

of hand that can be successfully detected with such

methods is limited due to scarce feature extraction

mechanism.

In this paper application of continuous skeleton

to real-time hand shape analysis is presented. Sim-

ilar approach was used in (Mestetskiy, 2007) for

shape comparison of ﬂexible objects. Palm silhou-

ette boundary is approximated as a polygon, and its

skeleton is constructed with help of Voronoi diagram

of line segments. Simple and efﬁcient pruning algo-

rithm helps to get rid of unimportant skeleton edges.

Hand silhouette skeletonization provides rich fea-

ture generation mechanism and allows performing

complex shape analysis, determining topology of the

hand (number and shape of visible ﬁngers), estimat-

ing relative location of palm parts and measuring

width of silhouette in arbitrary place. Moreover such

analysis can be performed regardless of palm orien-

tation in the frame. In addition computationally efﬁ-

cient skeletonization and pruning algorithms are suit-

able for usage in real-time applications.

The text of the paper is organized in a following

way. Review of the literature on the topic is given in

Section 2. The notion of the continuous skeleton is

given in Section 3. Application of skeleton analysis

for palm shape recognition is presented in Section 4.

Experiments are described in Section 5. And Section

6 completes the paper and states the conclusions of

555

Kurakin A. and Mestetskiy L..

HAND GESTURE RECOGNITION THROUGH ON-LINE SKELETONIZATION - Application of Continuous Skeleton to Real-time Shape Analysis.

DOI: 10.5220/0003315505550560

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2011), pages 555-560

ISBN: 978-989-8425-47-8

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

the research and future works.

This work is supported by the Russian Foundation

of Basic Researches (grant 08-01-00670).

2 RELATED WORK

The topic of gesture recognition is subjected to ac-

tive research, and a lot of different approaches to the

problem exist. Some of them are not widely used

due to requirement of complex experimental setup

(Schlattman and Klein, 2007) or expensiveequipment

such as instrumented gloves (Aguiar et al., 2009).

Among more available techniques color markers

could be used for hand tracking and gesture recogni-

tion. And there are a lot of methods which use only

image of hand obtained from the camera. Good re-

view of vision based method is presented in paper

(Garg et al., 2009).

In (Wang and Popovi´c, 2009) special colored

glove is used for hand pose estimation. The advan-

tage of this approach is high range of successfully es-

timated poses. Shortcomings include requirement to

wear the glove and increased requirement to the im-

age quality. Also pose estimation involved computa-

tionally expensive search in the database of available

poses, that’s why parallel algorithm shows only 10fps

on modern computer.

In papers similar to (Liu et al., 2008) hand pose

estimation is performed by the search in multidimen-

sional space of all possible hand conﬁgurations. How-

ever such approaches are computationally expensive

and can hardly be used in real-time applications.

Also bare hand tracking could be performed by

preliminary segmenting skin and non-skin regions in

the image and further analysis of regions correspond-

ing to hand. For example, in papers (Burger et al.,

2007) and (Dhawale et al., 2006) macro features (such

as size, position and Hu invariants) of palm silhouette

are used for hand gesture recognition. These methods

work fast but the set of detected gestures is poor and

the methods provide no way to evaluate location of

ﬁngers.

The most promising approach to shape analysis

is computation and analysis of skeleton of palm sil-

houette. In particular such approach is described in

(Beristain and Grana, 2010). In that paper skeleton

of palm silhouette is constructed and simple greedy

algorithm for skeleton comparison is used to classify

hand gestures into 3 classes. But the paper did not

cover ﬁnger detection and tracking as well as mea-

surement of different silhouette features. In addition

their skeletonization algorithm operates with discrete

boundary and requires development of complex prun-

ing methods given the fact that such methods not al-

ways provide acceptable result.

3 CONTINUOUS SKELETON

Methods considered in the paper are based on the no-

tion of the skeleton of a ﬁgure. The skeleton is a set of

points which are equidistant from two or more ﬁgure

borders.

In the literature there are two approaches of de-

scribing and constructing a skeleton: discrete and

continuous approaches. In the discrete case skele-

ton is described as the set of pixels, and it is con-

structed with help of pixel-based processing of the

original image. In the continuous case skeleton is de-

scribed as a union of points and curves. The advan-

tage of continuous approach is the fact that it is easier

to perform further processing on continuous skeleton

in comparison to discrete one. In this paper contin-

uous approach is used and all necessary deﬁnitions

are given below. Details about continuous skeletons

and the process of skeletonization could be found in

(Mestetskiy, 2010), (Mestetskiy and Semenov, 2008)

and (Siddiqi and Pizer, 2008).

Maximum inscribed circle is the closed circle C

that is completely lying inside the ﬁgure F, and any

other circle C

′

within the ﬁgure does not contain C:

∀C

′

⊂ F,C

′

6= C :C 6⊂ C

′

Skeleton of polygonal shape is the locus of cen-

ters of maximum inscribed circles. Also radius

of inscribed circle is associated with each point of

the skeleton, and such association between skeleton

points and radii is called radial function.

It can be proved that the skeleton of the polygon

consists of ﬁnite set of line segments and arcs of the

parabolas (Mestetskiy, 2010). So the skeleton could

be considered as a planar graph. And such skeleton

representation is called axial graph. Below in the ar-

ticle we use both graph and curve properties of skele-

ton, so terms axial graph and skeleton will be used

interchangeably.

Degrees of vertices in axial graph can be from 0 to

3. Each edge of this graph can be line segment or arc

of the parabola. Radius of maximum inscribed circle

is associated with each vertex of the graph and any

internal point of the edges.

The process of skeleton construction from binary

image is showed on the ﬁgure 1. Low resolution im-

age is chosen as an example: palm size is 36 pixels

and ﬁngers’ widths are about 5-6 pixels. Continuous

skeleton construction from binary image is described

in details in the book (Mestetskiy, 2009), but brieﬂy

algorithm consists of the following steps:

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

556

Figure 1: The process of skeleton construction. Left. Source

binary image and resultant skeleton. Middle. Boundary cor-

ridor and minimal perimeter polygon. Right. Skeleton be-

fore pruning.

1. Construction of Boundary Corridor of the Bi-

nary Image. For initial binary image (ﬁgure

1, left) boundary corridor is calculated based on

boundary tracing. Boundary corridor consists

of two sequences of pixels: black sequence and

white sequence. White sequence corresponds to

internal boundary of the corridor and black to ex-

ternal. On the middle part of the ﬁgure 1 corridor

is drawn in gray color.

2. Construction of Minimal Perimeter Polygon

Inside the Boundary Corridor. Closed path

of minimal perimeter is constructed inside the

boundary corridor. Such path will be closed con-

tour without self-intersections. Physical model

of the path is a rubber thread stretched along the

boundary corridor. Minimal perimeter polygon is

shown on the middle part of ﬁg. 1.

3. Skeleton Construction. Skeleton is constructed

for the minimal perimeter polygon. On the right

part of the ﬁgure 1 skeleton and maximum in-

scribed circles at the vertices of the axial graph

are drawn.

4. Skeleton Regularization. When skeleton is con-

structed it is subjected to pruning. Pruning is

performed by sequential cutting of certain ter-

minal edges of the skeleton. Cutting criteria is

based upon the following principle. Initial poly-

gon could be represented as a union of all in-

scribed circles with the centers at the skeleton

points. When skeleton edge is removed associated

circles are removed too. Union of the remaining

circles forms a ﬁgure which is called silhouette

of the remaining skeleton part. This silhouette is

a subset of the initial polygon and it is situated

inside it. If Hausdorff distance of this silhouette

and initial polygon is less than the threshold then

skeleton edge is cut, otherwise - not. In the exam-

ple on the ﬁgure 1 threshold is equal to 2 pixels.

In the rest of the article by skeleton we mean

pruned skeleton. Moreover due to the fact that

parabolic edges are usually short, they are approxi-

mately treated as line segments.

In the axial graph length of each edge is deter-

mined as Euclidean length of the correspondingskele-

ton segment. Lengths of the edges naturally generate

distance on the axial graph, in such a way that dis-

tance between two vertices can be calculated as the

total length of the edges in the shortest path between

these vertices.

4 PALM SHAPE ANALYSIS

4.1 Skeleton Branch and its Properties

Here we introduce the notion of skeleton branch

which is a part of skeleton treated as a continuous

curve.

Consider a continuous piecewise-smooth curve

without self-intersections~s(•) : s(l) = {x(l), y(l)},l ∈

[0,L], and let l be natural parameter of the curve (i.e.

arc length along the curve). Let each point of the

curve ~s(•) be a point of the skeleton. In such case

we will call the curve~s(•) as skeleton branch, which

connects points r(0) and r(L) of the skeleton

Radial function R(x,y) is known for each point P

of the skeleton, and its value is equal to the radius of

maximum inscribed circle with the center at point P.

Let’s deﬁne radial function along the branch~s(•) as

(l) = R(~s(l)),l ∈ [0, L].

Theorem. For any skeleton branch ~s(•) of the

skeleton of polygonal shape radial function along the

segment R

(l) is continuous and piecewise smooth

function.

The proof of the theorem is based on the fact

that the skeleton of polygonal shape is union of ﬁnite

number of line segments and arcs of parabolas, and

radial function R(x, y) along each such piece of the

skeleton is linear or quadratic function of coordinates

(Mestetskiy, 2010). So if we consider union of such

segments and consider natural parametrization along

them, value of radial function will be smooth along

each segment and continuous at the junctions of seg-

ments.

4.2 Linear Approximation of the Radial

Function

It is inconvenient to work numerically with values of

radial function along the branch due to presence of

parabolic arcs in the skeleton. So we replace the ini-

tial skeleton to its approximation without parabolic

arcs.

Let’s replace all parabolic arcs in the initial skele-

ton by line segments and call the new graph as lin-

early approximated skeleton.

HAND GESTURE RECOGNITION THROUGH ON-LINE SKELETONIZATION - Application of Continuous Skeleton

to Real-time Shape Analysis

557

For each point of linearly approximated skeleton

let’s introduce linearly approximated radial function

R(x,y) in the following way.

R(x,y) is equal to R(x,y)

for the vertices of the initial skeleton, and inside the

edges of approximated skeleton

R(x,y) changes lin-

early from one end of the edge to another.

Similarly to the source skeleton, let’s consider

skeleton branches and approximated radial function

along the branch

(x,y) for the approximated skele-

ton. It can be proven that such approximated radial

function is continuous and piecewise linear function

of its parameter.

4.3 Calculation of Approximated Radial

Function

Let’s consider two vertices A and B of the initial skele-

ton and simple path P in the axial graph between these

vertices. Path P uniquely deﬁnes skeleton branch~s(•)

and approximated skeleton branch ˜s(•). Approxi-

mated radial function along the branch ˜s(•) could be

easily calculated in the following way.

Denote vertices in the path P as V

A,V

,...,V

n−1

= B.

Denote the values of the radial function in these

vertices as R(V

) = R

Let L

be the length along the graph between ver-

tices A and V

, that is L

∑

i−1

k=0

k+1

In such notion approximated radial function along

segment

˜s

(l) could be calculated as:

˜s

(l) =











l = L

;

αR

+ (1− α)R

i+1

l = αL

+ (1− α)L

i+1

α ∈ (0,1)

4.4 Fingers Detection

Fingers detection is performed by analysis of skeleton

branches which ends in the dangling vertices. The

algorithm is described below.

Let A be an arbitrary dangling vertex of the axial

graph. Let B be the nearest (in terms of the distance

along the graph) to the A vertex of the axial graph

which degree is equal to 3.

Consider approximated skeleton branch ˜s(•) gen-

erated by the shortest path P between vertices A and

B, and consider approximated radial function

˜s

(l)

along the branch ˜s(•).

Samples of the function

˜s

(l) for two different

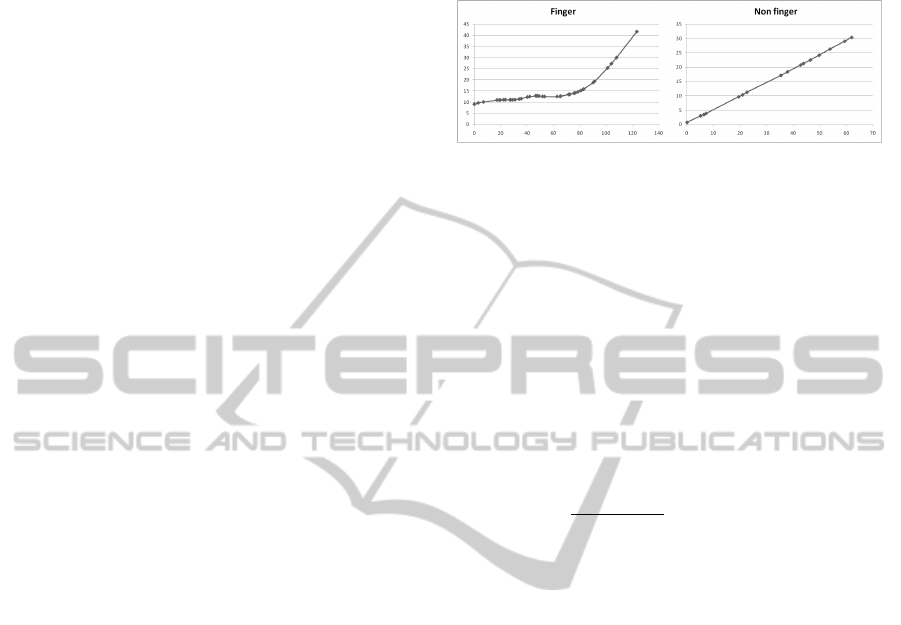
skeleton branches of palm silhouette from left part

of ﬁgure 3 are shown on ﬁgure 2. Left part of ﬁg-

ure 2 depicts

˜s

(l) for skeleton branch corresponding

to ﬁnger, and the right plot corresponds to non-ﬁnger

skeleton branch which starts from dangling vertex in

the bottom part of the palm.

Figure 2: Radial function for ﬁnger and non ﬁnger.

As it can be seen from the plots, there are distinc-

tive features associated with the length of the segment

and radial function values which can be used to dis-

tinguish segments of the axial graph corresponding to

ﬁngers from others. These distinctive features were

used to classify segments of the axial graph as ﬁngers

or non ﬁngers.

Here we use notation from the previous subsec-

tion (V

...,V

, R

...,R

and L

...,L

), and intro-

duce values D

which are discrete derivatives of R

. In the corner points let D

= 0, D

= +∞, and in

the rest points let D

be calculated by the formula:

i+1

− R

i−1

i+1

− L

i−1

, i = 1,...,n− 1

We use R

, L

and D

to estimate the position of

point C - point of articulation of ﬁnger and metacar-

pus. Given point C different features of the skeleton

branch, such as length, average width, distance to the

center of the palm, could be measured. And all these

values are used for ﬁngers classiﬁcation.

Search of point C is performed from the assump-

tion that at the end of the ﬁnger one of the following

conditions should be satisﬁed:

• R should increase in 2 - 2.5 times in comparison

with the beginning of the ﬁnger

• Radius starts to increase signiﬁcantly, i.e. discrete

derivatives D

are greater than the threshold

When the point C is found for the segment AB,

we calculate length of segments AB and AC as well

as width of segment AC. Width is calculated as the

value of radial function at predeﬁned point of AC or

as average value of the radial function on the AC. We

classify AB as a ﬁnger if all the following conditions

are met:

• |AC|/|AB| ≥ 0.35

• Width of AC lies in speciﬁed range

• Length of AB should be greater than the threshold,

i.e. ﬁnger should not be short

Result of the work of the described algorithm is

shown in the ﬁgure 3. Big blue circle is the circle of

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

558

maximal radius inscribed in the palm. The center of

this circle is considered as palm center. And small or-

ange circles correspond to ﬁngertips and articulations

of ﬁngers and metacarpus.

Figure 3: Fingers detection samples.

4.5 Gesture Recognition

Gesture recognition is performed by calculating rela-

tive movement of ﬁngers and the palm, and by calcu-

lating absolute movement of the palm as a whole. Us-

ing these values several gestures are recognized and

used in the demo-software. The list of the gestures is

following:

• One ﬁnger is seen (ﬁg. 3, right). The ﬁnger and

the palm are moving as a whole. This gesture is

used for cursor movement and object dragging in

the demo.

• Two ﬁngers are seen, and their ﬁngertips are mov-

ing along the straight line (ﬁg. 5). This gesture is

used for object zooming.

• Three ﬁngers are seen and form a triangle with

approximately constant lengths of the sides (ﬁg.

3, left). This gesture is used for object rotation.

• Big and pointing ﬁngers form a ring for a short

period of time (ﬁg. 4, right). This gesture is used

for object grabbing.

• All ﬁve ﬁngers are seen and spread wide apart for

a short period of time (ﬁg. 1). This gesture is used

for object releasing.

Gestures with 1,2,3 and 5 ﬁngers are detected eas-

ily with help of the algorithm from subsection 4.4.

Circles with the centers in the dangling vertices of

skeleton branches corresponding to ﬁngers are treated

as ﬁngertip positions. These circles along with de-

tected junction points of ﬁngers and metacarpus are

drawn orange in ﬁgure 3.

Metacarpus movement detection and palm scale

measurement is performed using position and radius

of inscribed circle which radius is maximal among all

inscribed circles and center is at the vertex of axial

graph with degree 3. This circle is shown in blue at

the ﬁgure 3.

Ring gesture is detected by ﬁnding cycles in the

Figure 4: Cycles in skeleton. Cycle on the left corresponds

to non-ring gesture and cycle on the right corresponds to

ring gesture.

axial graph. It should be noted that only cycles which

contain vertices near the center of the palm (blue cir-

cle) are treated as valid cycles (see ﬁgure 4), because

only such cycles are formed from ring between big

and pointing ﬁngers. Such classiﬁcation of cycles is

possible due to the fact that coordinates of each vertex

is known in the axial graph. Moreover to detect ring

gesture, we do not need to analyze contours of palm

silhouette and should only use axial graph.

Five ﬁngers and ring gestures are detected as dy-

namic gestures, that is time when the gesture observed

is measured, and gesture counts only if it has been ob-

served for predeﬁned time interval. Dynamic gesture

recognition is possible due to fast frame processing.

5 EXPERIMENTS

Software system was developed to demonstrate and

evaluate proposed gesture recognition method. This

system allows movement, zoom and rotation of sev-

eral objects on the screen of computer, and all the con-

trol is performed by means of gestures.

The following scheme of experimental setup was

used. Conventional consumer web-cam (Logitech

9000) was situated above the homogenous dark sur-

face.

In order to obtain palm silhouette per-pixel skin

detection is performed on the image obtained from

the web-cam (Vezhnevets et al., 2003; Phung et al.,

2005).

Continuous skeleton is constructed for the ob-

tained palm silhouette. And the skeleton was ana-

lyzed by algorithms described in the section 4. As

a result, gestures mentioned in the subsection 4.5 was

detected and used for object movement, zoom and ro-

tation. Figure 5 shows screen shot of the developed

software.

Effective algorithms for skeleton construction and

pruning make it possible to use the system in real-

time application. For example, single threaded im-

plementation of frame processing (including skin re-

gions segmentation, skeleton construction, pruning,

HAND GESTURE RECOGNITION THROUGH ON-LINE SKELETONIZATION - Application of Continuous Skeleton

to Real-time Shape Analysis

559

Figure 5: Sample screen shots of the software for experi-

ments. This image demonstrates gesture which was used

for object scaling.

gesture recognition and drawing of the result) takes

about 22 ms per frame on 2.4Ghz Intel Core 2 Quad

CPU, which gives 45fps.

6 CONCLUSIONS

Method of the palm shape analysis by the continu-

ous skeleton is considered in the paper. This method

allows wide range of palm silhouette features to be

measured, which is hard or even impossible to mea-

sure with other approaches. Moreover high process-

ing speed makes this method suitable for real-time ap-

plications.

We are going to extend considered approach by

adding the second camera to the setup. Image ob-

tained from the second camera will be subjected to

similar processing, and obtain pairs of coordinates of

each ﬁnger will be used for calculation of 3d positions

of hand and ﬁngers. For occlusion handling and esti-

mation of exact hand pose we are going to use hand

model.

In addition, we are going to apply the method

for development of convenient and fast systems for

human-computer interaction and virtual reality appli-

cations (Aguiar et al., 2009).

REFERENCES

Aguiar, R., Pereira, J. M., and Braz, J. (2009). Gadevi -

game development integrating tracking and visualiza-

tion devices into virtools. In GRAPP 2009: Proc. of

Int. Conf. on Computer Graphics Theory and Ap-

plications, pages 313–321. INSTICC Press.

Beristain, A. and Grana, M. (2010). A stable skeletonization

for tabletop gesture recognition. In Computational

Science and Its Applications ICCSA 2010, volume

6016 of Lecture Notes in Computer Science, pages

610–621. Springer Berlin / Heidelberg.

Burger, T., Urankar, A., Aran, O., Akarun, L., and Caplier,

A. (2007). Cued speech hand shape recognition - be-

lief functions as a formalism to fuse svms and expert

systems. In VISAPP 2007: Proc. of 2

Int. Conf. on

Computer Vision Theory and Applications, volume 2,

pages 5–12. INSTICC Press.

Dhawale, P., Masoodian, M., and Rogers, B. (2006). Bare-

hand 3d gesture input to interactive systems. In

CHINZ ’06: Proc. of the 7th ACM SIGCHI New

Zealand chapter’s int. conf. on Computer-human in-

teraction, pages 25–32, New York, NY, USA. ACM.

Garg, P., Aggarwal, N., and Sofat, S. (2009). Vision based

hand gesture recognition. World Academy of Science

Engineering and Technology, pages 972–977.

Liu, T., Liang, W., and Jia, Y. (2008). 3d articulated hand

tracking by nonparametric belief propagation on fea-

sible conﬁguration space. In VISAPP 2008: Proc. of

Int. Conf. on Computer Vision Theory and Appli-

cations, volume 2, pages 508–513. INSTICC Press.

Mestetskiy, L. (2007). Shape comparison of ﬂexible ob-

jects - similarity of palm silhouettes. In VISAPP

2007: Proc. of 2

Int. Conf. on Computer Vision The-

ory and Applications, volume 1, pages 390–393. IN-

STICC Press.

Mestetskiy, L. (2009). Continuous morphology of binary

images: ﬁgures, skeletons, circulars. Moscow: Fiz-

matlit (in Russian).

Mestetskiy, L. (2010). Skeleton representation based on

compound bezier curves. In VISAPP 2010: Proc. of

Int. Conf. on Computer Vision Theory and Appli-

cations, volume 1, pages 44–51. INSTICC Press.

Mestetskiy, L. and Semenov, A. (2008). Binary image

skeleton - continuous approach. In VISAPP 2008:

Proc. of 3

Int. Conf. on Computer Vision Theory and

Applications, volume 1, pages 251–258. INSTICC

Press.

Mitra, S. and Acharya, T. (2007). Gesture recognition: A

survey. IEEE Transactions on Systems, Man and Cy-

bernetics - Part C, 37(3):311–324.

Phung, S. L., Bouzerdoum, A., and Chai, D. (2005). Skin

segmentation using color pixel classiﬁcation: Analy-

sis and comparison. IEEE Trans. Pattern Anal. Mach.

Intell., 27(1):148–154.

Schlattman, M. and Klein, R. (2007). Simultaneous 4 ges-

tures 6 dof real-time two-hand tracking without any

markers. In VRST ’07: Proceedings of the 2007 ACM

symposium on Virtual reality software and technology,

pages 39–42, New York, NY, USA. ACM.

Siddiqi, K. and Pizer, S. (2008). Medial Representations:

Mathematics, Algorithms and Applications. Springer

Publishing Company, Incorporated, 1st edition.

Vezhnevets, V., Sazonov, V., and Andreeva, A. (2003). A

survey on pixel-based skin color detection techniques.

In Proceedings of the GraphiCon 2003, pages 85–92.

Wang, R. Y. and Popovi´c, J. (2009). Real-time hand-

tracking with a color glove. ACM Transactions on

Graphics, 28(3).

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

560