AUGMENTED REALITY SYSTEM FOR KEYHOLE SURGERY

Performance and Accuracy Validation

Juan José Fuertes, Fernando López-Mir, Valery Naranjo, Mario Ortega

Eliseo Villanueva and Mariano Alcañiz

Instituto Interuniversitario de Investigación en Bioingeniería y Tecnología Orientada al Ser Humano

Universidad Politécnica de Valencia, Camino de Vera s/n, 46022 Valencia, Spain

Keywords: Augmented reality, 3D-virtual model, Validation, Laparoscopic surgery, Trocars.

Abstract: This work presents the performance and validation of an augmented reality (AR) system to help the surgeon

for trocar placement in laparoscopic surgery. The virtual organs are obtained by taking previous computed

tomography (CT) or magnetic resonance (MR) images of the patient and by applying segmentation

methods. Once in the operating theater, a real-time image of the patient is captured with a regular camera

that detects the patient’s pose (position + orientation) thanks to a marker that is centered on the navel. Then,

3D virtual organs are registered and fused with the real-time image, helping the surgeon to know the points,

at where, to place the trocars. To validate the system’s accuracy and performance, a 3D jar-model is

extracted from CT images which is then registered and fused with the real-time jar-image. An error of 2.91

millimeters is measured when the system accuracy is tested.

1 INTRODUCTION

Laparoscopy surgery is a surgical technique that

gives the surgeon a view into the patient’s internal

space with only small incisions. Nowadays, it offers

many advantages over traditional methods: smaller

incisions, lower probability of infection, the

prevention of consecutive operations, etc. There is a

faster recovery of the patient and fewer

psychological distresses. Nevertheless, laparoscopic

surgery has some drawbacks that are caused by the

inaccuracy of the points where the surgeon makes

keyhole incisions since a possible displacement

when the points are selected may give rise to a more

invasive surgery. Even experienced surgeons

sometimes require the replacement of trocars when

the surgery becomes complicated. Also, the lack of

direct vision and tactile perception as well as the

need for eye-hand coordination can be serious

problems. Therefore, the development of an accurate

system that helps surgeons improve their

performance is desirable.

The work that is developed in this project

validates the performance and accuracy of an

augmented reality system for placing trocars in

patients’ bodies. Many authors explain techniques

that attempt to improve and automate the location of

trocars: by taking CT or MR images and applying

automatic or semi-automatic segmentation methods,

a 3D virtual model of the organs is obtained. Then,

the surgeon must remember that information

because there is no software in the operation theater

that can show both the patient and the virtual model

at the same time. Chiu, Dey, Drangov, Boyd, and

Peters (2000) propose an external system for trocar

placement to obtain optimal access to the organs and

to simulate the endoscopic view observed by the

surgeon. The validation of the system is performed

using a phantom. Cannon, Stoll, Selha, Dupont,

Howe, and Torchiana (2003) convert the problem of

trocar placement into a mathematical problem that is

interesting for robot-assisted surgery. Adhami and

Coste-Manière (2003) convert the same problem

into an optimization problem where visibility and

dexterity are the cost function. The validation is

made with animals. Scheuering, Schenk, Schneider,

Preim, and Greiner (2003) use fiducials to register

the image and the virtual model, but these fiducials

must be visible when CT images and volume

reconstruction are obtained. In addition, they must

be in the same position once the patient is inside the

operation theater.

There are more techniques that are related to our

273

Fuertes J., López-Mir F., Naranjo V., Ortega M., Villanueva E. and Alcañiz M..

AUGMENTED REALITY SYSTEM FOR KEYHOLE SURGERY - Performance and Accuracy Validation.

DOI: 10.5220/0003316002730279

In Proceedings of the International Conference on Computer Graphics Theory and Applications (GRAPP-2011), pages 273-279

ISBN: 978-989-8425-45-4

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: The block diagram of the AR system.

work, where the 3D virtual model is shown along

with the patient’s image once the patient is in the

operation theater. In this way, the surgeon has the

information in-situ when the operation is going to

start. Trevisan, Nicolas, Delville, Cornet d’Elzius

and Macq (2004) describe a technique to merge 3D

virtual models onto real scenes without tracking

markers. With the use of stereovision technique they

show a minimum error of 1 mm but an average error

of 1 cm in translation. Pandya, Siadat and Auner

(2005) propose a prototype medical Augmented

Reality system and they analyze the individual error

contributions and the system accuracy with an error

of 2.74 mm on average. Feuerstein, Wildhirt,

Bauernschmitt, and Navab (2005) propose an

automatic registration method where the fiducials

that are used to track the laparoscopic camera have

to be in the same place as in the CT images.

Afterwards, Feuerstein, Mussack, Heining and

Navab (2008) incorporate the superposition of the

3D virtual model in the laparoscopic camera.

Volonte, Bucher, Pugin, Carecchio, Sugimoto,

Ratib, and Morel (2010) perform registration and

fusion with the anatomical knowledge of the

surgeon. Our work incorporates a semi-automatic

registration and fusion method using markers, which

is validated with a 3D virtual model.

In summary, the goal of this project is to provide

the surgeon with information about locating trocars

in the patient. Section 2 shows a functional block

diagram of the augmented reality system (see Figure

1), explaining briefly how the 3D model is obtained

and located in a 3D work-screen-space. This section

also details the technique used when registering and

fusing. Section 3 and 4 show the empirical

experiments and the obtained results. Finally,

Section 5 presents conclusions and future work.

2 METHODOLOGY

2.1 Functional Block Diagram

This section explains how the AR system based on

the development of an application for laparoscopic

surgery works. It allows the surgeon to see “the

inside” of the patient’s body at the same time that

incisions are being made.

The AR system is divided into two blocks

(Figure 1). In the first block, before the operation

starts, the 3D virtual model of the organs is obtained

and is placed in a 3D-screen space together with the

images. Then, a change in the coordinate system in

the 3D-space is performed (Schroeder, Martin, and

Lorensen, 2006) in order to place the new origin in

the navel, keeping the orientation of the organs in

CT/MR images.

In the second block the real-time patient-image is

shown and the patient’s pose (position + orientation)

is automatically detected in the real world thanks to

a marker centered on the navel (see Figure 2). This

is what allows the 3D model and the image to be

registered and fused.

(a) (b)

Figure 2 (a): A Binary hexadecimal code marker; (b): The

AR system of the patient’s organs.

Registration and fusion

Patient

3D model

extraction

MR/CT Images

3D virtual model focused on the new

origin

Locating the navel

Patient

Real-Time Image

Real-time image with a

detected-marker

Mark centered on patient’s navel

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

274

2.2 Obtaining a 3D Model

When the CT/MR images are being obtained, the

patient must be perfectly still while lying on the

stretcher with his/her back straight and centered on

both sides in order to determine the orientation of

the organs with respect to an initial coordinate

system. 512x512 pixels CT/MR images with a

spacing resolution of 0.938x0.938x3.0 millimeters

(mm) in each coordinate axis are obtained from a

General Electric Signa Excite 1.5T NVP 73800, and

then, the virtual model of different organs is

extracted by applying digital image processing,

especially a region growing algorithm and other

algorithms developed in the ITK library by Ibanez,

Schroeder and Cates (2005).

Once in the operation theater, the surgeon selects

the point of the navel in the CT/MR images thanks

to the application presented here. This application

establishes the new origin of the images and the

model at that point (see Figure 3). Thus, the organs

are oriented as in the CT/MR images, but in a

different position due to the coordinate change. The

new coordinate system after the change is:



= ∝+ x;



= β +y;



+ z;

(1)

where α, β, and γ are the coordinates of the patient’s

navel with respect to the initial coordinate system

(x,y,z).

Figure 3: Coordinate system change.

2.3 Camera Calibration

To take the real-time image, a Logitech QuickCam

Pro 9000 webcam is used, which shows the area of

interest constantly. First, the camera is calibrated to

avoid possible errors when capturing images.

To do this, it is necessary to have different

captures of planar checkerboard patterns (see Figure

4), which should be different for each calibration

image. Zhang’s method (2000) is used for the

calibration step, taking the correspondence between

2D image points and 3D scene points over a number

of images.

The camera 3x3 intrinsic matrix K and the vector

γ with the distortion parameters have the following

form:

K = 

0α

001

 γ = 











(2)

where f is the focal length, (u, v) is the camera

optical centre, α is the aspect ratio, and s is the

camera skew between the x- and y-axes; α

and α

are the radial distortion parameters, and β

and β

are

the tangential distortion parameters.

Next, a marker that is centered on the navel is

placed as shown in Figure 2 (a) to register and fuse

the image and the 3D virtual model of the organs. It

is advisable to keep the camera parallel to the

patient’s trunk in order to improve the accuracy of

the system, as is shown in Section 4.

(a) (b)

Figure 4 (a): Checkerboard that is used to calibrate the

camera; (b): A Logitech QuickCam Pro 9000 webcam.

2.4 Marker Detection, Registration,

and Fusion

A binary hexadecimal code marker of 8.45x8.45

centimeters is used in this step. First, the RGB

captured image is converted to a binary image, and

the edge of the marker is detected thanks to an

adaptive threshold algorithm based on the technique

of Pintaric (2003). Basically, “this technique

evaluates the mean pixel luminance over a

thresholding region of interest, which is defined as a

bounding rectangle around the marker axis-aligned

corner vertices in the screen-space”.

Afterwards, the relative marker position and

orientation with respect to the camera (view point)

can also be estimated from a planar structure when

the internal parameters are known, in order to apply

them to the virtual model. First, a 3D/2D

homography matrix must be calculated to later

obtain the projective matrix, as detailed by Martin-

Gutierrez, Saorín, Contero, Alcañiz, Pérez-López,

and Ortega (2010).

AUGMENTED REALITY SYSTEM FOR KEYHOLE SURGERY - Performance and Accuracy Validation

275

A 3D/2D correspondence (m, M) includes a 3D

point M and a 2D pixel point m, which are

represented as (X,Y,Z,1) and (x,y,1)

, respectively.

(m, M) is related by the 3x3 projective matrix P

Hartley and Zisserman (2003) show:

m= λ



M, P







]

(3)

where R

is a 3x3 rotation matrix, t

is the translation

vector of the camera, and λ

is the homogeneous

scale factor that is dependent on P

M. Specifically,

considering the z=0 plane, the expression of the

homography that maps a point onto this plane and its

corresponding 2D point m under the perspective can

be recovered by writing:



=m=















=















(4)

where R

, R

, and R

are the columns of the matrix

R. Thus, (m, M) is related by a 3x3 matrix H

, called

homography matrix:



=









, H















(5)

Conversely, once H

and K are known, the

patient’s pose can be recovered from equations (3)

and (5), because R is a unit orthogonal matrix, as

Simon, Fitzgibbon, and Zisserman (2000) explain

(“the last column R

is given by the cross-product

×R

”):

















, P















(6)

Generally, the patient’s pose can be refined by

nonlinear minimization, since the anterior processes

are sensitive to noise and, therefore, a lack of

precision and the “jitter” phenomenon are produced.

In this case, the sum of the reprojection errors is

minimized, which is the squared distance between

the projection of the 3D points and their measured

2D coordinates. We can therefore write:





]

=argmin







|



]

PM



− m







(7)

This equation will be solved using the

Levenberg–Marquardt (LM) algorithm proposed by

Marquardt (1963)

, providing a solution for the

problem “Nonlinear Least Squares Minimization”.

In this way, the 3D virtual model and the

patient’s image can be registered and fused,

allowing the surgeon to vary the transparency of the

image to see the patient’s image as shown in Figure

5. Just then, it is important for the patient to

maintain his/her position to avoid possible

registration errors.

Figure 5: The developed AR application. 3D-screen-space.

3 EXPERIMENTS

In order for the system to be validated by the

surgeon in the hospital, to test how the AR module

works, and to determine its accuracy, the following

experiments were performed using a 22 inch display,

a i5 4.0 GB RAM computer, and a regular camera.

Initially, 512x512 CT images with a spacing-

resolution of 0.488x0.488x0.625 mm per pixel were

extracted from a jar by means of a GE LightSpeed

VCT – 5124069 machine. The model used was a

500 ml DURAN GLS 80 jar with a diameter of 101

mm. The 3D virtual model was obtained by applying

a region growing algorithm to 8- and 12- bit images.

In the first experiment, to extract the virtual

model, a region growing algorithm was applied to 8-

bit images (which were rescaled from the initial 12-

bit images), taking the pixels between thresholds

230 and 255 gray scale. In the second experiment,

the region growing algorithm was applied to 12-bit

images, but taking the pixels between thresholds 150

and 2200 Hounsfield Units (HU).

Figure 6: Experimental assembly of the system.

The camera was placed at a 90º degree angle

relative to the real jar, as shown in Figure 6. Then,

the middle point of the jar was selected in the CT

images as the new origin, and the marker was

centered on the jar. The registration and fusion were

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

276

performed at that moment, taking an image of the

real jar and the virtual jar to validate the system’s

accuracy. A full graphic example of the experiment

is shown in Figure 7.

(a) (b)

Figure 7 (a): CT jar images; (b): 3D jar model in screen-

space; (c): Marker on the jar; (d): Real jar and virtual jar.

The positions where the accuracy was tested are

shown in Figure 8:

Figure 8: Positions where the measurements are taken.

4 RESULTS

In the first experiment, 8 test-samples were

performed to calculate the system’s accuracy by

placing the camera 50 cm away from the center of

the marker placed on the real jar and aligning it.

In each test, the real jar was removed and

relocated to the initial position. The 3D virtual

model of the jar was obtained from 8 bit-images.

The width of the real jar in the image was measured

in each position. The width of the 3D virtual jar was

also measured, obtaining the difference between the

widths (see Figure 9 (a)). After working out the

average of the 8 test samples, the results obtained in

pixels were:

Table 1: Results obtained with the virtual jar extracted

from 8-bit images.

JAR 0º POS. 1 POS. 2 POS. 3 POS. 4 Pref

Real Width

(pixels)

79 82 104 104 104

Model Width

(pixels)

73 78 100 99 99

Difference (pixels) 6 4 4 5 5

The average error was 5 pixels. Then, a new

model was obtained by applying a region growing

algorithm to 12 bit-images. Thus, it was possible to

compare both experiments in order to know if the

segmentation technique had any special influence on

the final accuracy. Eight samples were taken under

similar conditions to the first experiment (keeping

the camera at the same position and relocating the

jar). Table 2 shows the results:

Table 2: Results obtained with the virtual jar extracted

from 12-bit images.

JAR 0º POS. 1 POS. 2 POS. 3 POS. 4 Pref

Real Width (pixels) 79 82 104 104 104

Model Width

(pixels)

76 81 102 101 101

Difference (pixels) 3 1 2 3 3

The average error was 3 pixels. Since the width

of the real jar and the width in the image are known,

it is possible to calculate the equivalence mm-pixel.

In this case, 1 mm = 1.030 pixels, so the error

average was 2.913 millimeters.

As Table 2 shows, the error decreases due to the

higher accuracy when the model is segmented with a

region growing algorithm to 12-bit image resolution.

(a) (b)

Figure 9: (a): The real jar and virtual jar image with

camera position 0º relative to the real jar; (b): The real jar

and virtual jar with camera position 5º relative to the real

jar.

Pos. 1

Pos. 2

Pos. 3

Pos. 4

Pref

AUGMENTED REALITY SYSTEM FOR KEYHOLE SURGERY - Performance and Accuracy Validation

277

Three other experiments were performed to

analyze the evolution of the error relative to the

angular position of the camera. The camera angles

used were 5º, 10º, and 15º relative to the initial

position. In this case, since the virtual model hides

part of the real jar in the image (see Figure 9 (b)),

the difference in the right edge was calculated. Table

3 shows the results:

Table 3: Results obtained with 5º, 10º, and 15º deviation

camera and virtual jar extracted from 12-bit images.

JAR 5º POS. 1 POS. 2 POS. 3 POS. 4 Pref

Difference

(pixels)

4 2 2 3 3

JAR 10º POS. 1 POS. 2 POS. 3 POS. 4 Pref

Difference

(pixels)

5 4 4 4 4

JAR 15º POS. 1 POS. 2 POS. 3 POS. 4 Pref

Difference

(pixels)

8 9 7 7 7

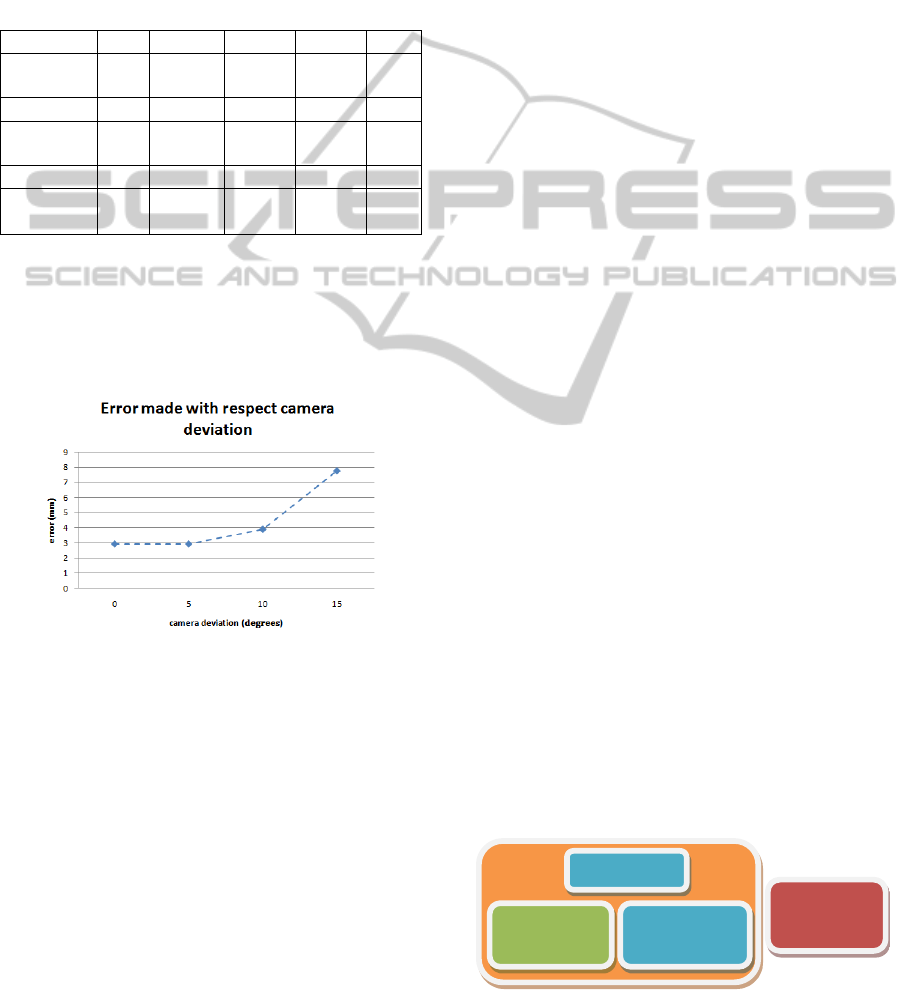
When the deviation was 5º, the error was similar

to case 1 (3 pixels), however, when it was 10º or 15º,

the error increased considerably (4 pixels and 8

pixels respectively). The higher the deviation

between the camera and the marker, the lower the

accuracy of the method, as Figure 10 shows.

Figure 10: Error made relative to the angular position of

the camera.

5 DISCUSSION

AND CONCLUSIONS

In this paper, we have presented a method to help

surgeons place trocars in laparoscopic surgery.

The minimum accuracy required for minimally

invasive surgery in the insertion of trocars is

approximately 2 centimeters (cm) because both skin

and trocars have a maximum error correction of 2

cm to compensate for locating errors as explained by

Feuerstein (2007). Therefore, it is important for the

CT/MR images to have a resolution that is higher

than 2 cm in all directions in order to segment and

obtain the 3D model correctly. This is a requisite

that is easy to carry out because the resolution of the

images used is only a few millimeters. If images had

a resolution lower than 2 cm, the system would not

be useful for surgeons.

Furthermore, since the segmentation method

employed in reconstruction of the 3D virtual organs

has a global influence on the system accuracy, it is

better to work with a high resolution image (12 bits)

than with 8-bit images (as proven in Section 4). If

the segmentation method or the image resolution are

not optimized, the global system will not work very

well even though the registration is adequate.

It is also important to emphasize how to place

the marker on the patient since it must be centered

on the navel and its base aligned horizontally. It

must be on a flat plane to avoid loss of accuracy

when the pose is calculated.

Analyzing the graphic and numerical results, we

can conclude that registration and fusion satisfy the

requirements. To be more thorough, the numerical

results that have been obtained lead to the

conclusion that the system can be used with patients

because, when it is well-calibrated, the error is only

about 3 mm. Again, note that the higher the

deviation between the camera and the marker, the

lower the accuracy of the method, emphasizing the

importance of camera position.

This result stands with regard to existing AR

methods: Pandya, Siadat and Auner (2005) showed

an error of 2.74 mm on average with standard

deviation of 0.81 mm in neurosurgery; Trevisan,

Nicolas, Delville, Cornet d’Elzius and Macq (2004)

presented an error of 1 mm but the object must be at

the centre of the sight (camera). Otherwise, the

system works badly; Feuerstein, Wildhirt,

Bauernschmitt and Navab (2005) showed a tracking

average error of 2.6 mm on a rigid phantom.

Another important topic is that the human’s liver

is deformable and non static, so it would desirable to

know the real-time deformation that the liver

undergoes. This is the reason why the AR system

proposed in this work belongs to a global system

that is currently being developed, as it is shown in

Figure 11.

Figure 11: General system for keyhole surgery.

Navigation

System

Segmentation

System

Biomechanical

Model

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

278

All these assumptions (the patients must keep

their pose during scan and location of the trocars, the

liver is not rigid and dynamic, the surgeon aligns the

mark and places it on a flat plane, etc.) will be

overcome since the AR module is introduced in the

global system. It will allow the system to be

acceptable in a clinical environment once the

clinicians validate the accuracy and performance of

the system.

In addition, for future work, we plan the

insertion of tracking algorithms to control the

patient’s position, studying the different kinds of

markers.

ACKNOWLEDGEMENTS

This work has been supported in part by the project

IMIDTF/2009/83 and by private funds from

Beanaca s.a. We would like to express our deep

gratitude to the Hospital Clínica Benidorm for its

participation in this project.

REFERENCES

Adhami L. and Coste-Manière É. (2003). Optimal

planning for minimally invasive surgical robots. IEEE

Transactions on Robotics and Automation (Vol. 19,

Sup. 5, pp. 854–863).

Cannon J., Stoll J., Selha S., Dupont P., Howe R., and

Torchiana D. (2003). Port placement planning in

robot-assisted coronary artery bypass. IEEE

Transactions on Robotics and Automation, (Vol. 19,

pp. 912–917).

Chiu A. M., Dey D., Drangova M., Boyd W. D., and

Peters T. M. (2000). 3-D image guidance for

minimally invasive robotic coronary artery bypass.

The Heart Surgery Forum (Vol. 3, pp. 224–231).

Feuerstein M. (2007). Augmented Reality in laparoscopic

surgery. Tésis Facultad de Informática, Universidad

Politécnica de Múnich.

Feuerstein M., Mussack, T., Heining S. M. and Navab N.

(2008). Intra-operative laparoscope augmentation for

port placement and resection planning in minimally

invasive liver resection. IEEE Transactions on

Medical Imaging. (Vol. 32, Sup. 3, pp. 355-369).

Feuerstein M., Wildhirt S. M., Bauernschmitt R. and

Navab N. (2005). Automatic patient registration for

port placement in minimally invasive endoscopic

surgery, in Proc. Int’l Conf. Medical Image

Computing and Computer Assisted Intervention

(MICCAI). (Vol. 3750, pp. 287–294).

Gonzalez, Rafael C., Woods, Richard E. and Eddins,

Steven L., (2004). Digital Image Processing Using

MATLAB. Pearson Prentice Hall, (chapters 9-12),

Upper Saddle, NJ.

Hartley R. and Zisserman A. (2003). Multiple View

Geometry. In Computer Vision, Second Edition,

Cambridge University Press.

Ibanez, Schroeder, Ng, Cates. (2005). The ITK software

Guide, published by Kitware Inc,.

Marquardt Donald, (1963). An Algorithm for Least-

Squares Estimation of Nonlinear Parameters. SIAM

Journal on Applied Mathematics. (Vol. 11, pp. 431–

441).

Martin-Gutierrez, J., Saorin, J. L., Contero, M., Alcañiz

M., Pérez-López David C., Ortega M. (2010,

February). Education: Design and validation of an

augmented book for spatial abilities development in

engineering students. Computers and Graphics. (Vol.

34 (1), pp. 77-91).

Pandya A., Siadat M., Auner G. (2005). Desing,

implementation and accuracy of a prototype for

medical augmented reality. Computer Aided Surgery.

(Vol. 10 (1), pp. 23-35).

Pintaric T. (2003). An adaptive thresholding algorithm for

augmented reality toolkit. In: Proceedings CD of the

second IEEE international augmented reality toolkit

workshop, ART03.

Scheuering M., Schenk A., Schneider A., Preim B., and

Greiner G. (2003). Intraoperative augmented reality

for minimally invasive liver interventions. In Medical

Imaging 2003: Visualization, Image-Guided

Procedures, and Display. Proceedings of SPIE, (Vol.

5029, pp. 407-417).

Simon G., Fitzgibbon A. W., and Zisserman A., (2000,

October 5-6). Markerless Tracking using Planar

Structures in the Scene. Proceedings of ISAR2000,

(pp. 120-128).

Trevisan, D., Nicolas, V., Delville, P., d'Elzius, M. C. and

Macq, B., Towards markerless augmented medical

visualization. In: MICCAI International Workshop on

Augmented Environments for Medical Imaging and

Computer-aided Surgery.

Volonte, F., Bucher, P., Pugin, F., Carecchio, A.,

Sugimoto, M., Ratib, O., Morel, P. (2010 June). Mixed

reality for laparoscopic distal pancreatic resection.

(Vol. 5, Sup. 1, pp. 122-130).

Schroeder W., Martin K., Lorensen B. (2006).

The

Visualization Toolkit, Fourth Edition.)

Zhang Z. (2000). A flexible new technique for camera

calibration. IEEE Transactions on Pattern Analysis

and Machine Intelligence. (Vol. 22 (11), pp. 1330–

1334).

AUGMENTED REALITY SYSTEM FOR KEYHOLE SURGERY - Performance and Accuracy Validation

279