A UNIFIED APPROACH TO GEOMETRIC MODELING OF
CURVES AND SURFACES
L. H. You and Jian J. Zhang
National Centre for Computer Animation, Bournemouth University, Bournemouth, U.K.
Keywords: Surfaces and curves, Static and dynamic geometric modeling, Partial differential equations.
Abstract: A unified approach to geometric modeling of curves and surfaces is given. Both a vector-valued fourth and
sixth order partial differential equations (PDEs) of motion are proposed. The fourth order PDE covers all
existing PDEs used for surface modeling, and the sixth order PDE considers the curvature effect on curves
and surfaces. In order to apply these PDEs to create curves and surfaces in real time, we have presented a
composite power series method which guarantees the exact satisfaction of boundary conditions, and
represents curves and surfaces with analytical mathematical formulae. We have examined the accuracy and
efficiency of the proposed method, and employed it to a number of applications of static and dynamic
modeling of curves and surfaces, including free-form surface generation and surface blending. It is found
that this method has similar computational accuracy and efficiency to the corresponding closed form
solution method, and creates curves and surfaces far more efficiently and accurately than numerical
methods. In addition, it can deal with complicated shape modeling problems.
1 INTRODUCTION
Free-form surfaces and curves are conventionally
created by surface modelers, such as Bézier, B-
spline and NURBS (Farin, 1997). Normally,
designers obtain control over the shape of a curve or
surface by adjusting control points. This involves a
lot of manual manipulations, especially when a large
number of control points are involved. To overcome
this weakness, active research is being undertaken
for many complementary free-form modeling
approaches. (Hyodo, 1990) proposed a method
generating a free-form surface defined by contours
and sectional curves. (Miura, 2000) proposed a unit
quaternion integral curve which is used to specify
the tangent of a curve in order to manipulate its
curvature more directly. (Ochiai and Yasutomi,
2000) demonstrated a method of generating a free-
form surface using the boundary integral equation.
With the drive towards realism, especially in
computer animation, physically-based modeling
represents another on-going research area where
forces, dynamics and time-dependent deformation
are considered. (Terzopoulos et al., 1987) employed
continuous elasticity theory to model the shapes and
motions of deformable bodies. Later on, this model
was extended to viscoelasticity, plasticity and
fracture (Terzopoulos and Fleischer, 1988), and
dynamic deformations (Terzopoulos and Qin, 1994),
(Qin and Terzopoulos, 1995). (Celniker and
Gossard, 1991) developed curve and surface finite
elements for interactive sculpting of curves and
surfaces. By minimizing the energy functional of a
surface, (Vassilev, 1997) proposed an interactive
sculpting method for deformable non-uniform B-
splines. With introduction of bar network
mechanics, a deformation method of surfaces was
developed (Guillet and Léon, 1998). A
comprehensive survey into physics-based modeling
methods was made by (Nealen et al., 2006) which
reviews the existing finite element/difference
/volume methods, mass-spring systems, meshfree
methods, coupled particle systems and reduced
deformable models based on modal analysis.
However, all these methods have to solve a large
set of linear algebra equations, hence are
computationally expensive and require large
computer memory.
Surface blending, another important application
field of shape modeling, has also been an active
research subject and many methods have been
developed. (Vida et al., 1994) classified methods of
constructing parametric blends as rolling-ball based
blends, spine-based blends, trimline-based blends,
blends based on polyhedral methods and other
23
You L. and Zhang J..
A UNIFIED APPROACH TO GEOMETRIC MODELING OF CURVES AND SURFACES.
DOI: 10.5220/0003316300230030
In Proceedings of the International Conference on Computer Graphics Theory and Applications (GRAPP-2011), pages 23-30
ISBN: 978-989-8425-45-4
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

methods including a cyclicde solution, PDE based-
blends and the Fourier-based blends.
The PDE based methods, since their advent two
decades ago, have found their applications in a lot of
surface modeling tasks, including free-form surface
generation (Bloor and Wilson, 1990a), n-sided patch
modeling (Bloor and Wilson, 1989a), surface
blending (Bloor and Wilson, 1989b), and industrial
applications (Athanasopoulos et al., 2009).
Compared with the conventional surface modeling
methods, the PDE-based methods provide the user
with a higher level control of the shape of the
generated surfaces using the parameters and the
boundary conditions of the PDE instead of many
hundreds of control points. Therefore they can be
easily implemented as an easy to use interactive
modeling package. However, before that can be
realized, we need to overcome one serious hurdle,
that is to solve the corresponding PDE efficiently.
Currently, it is done either ad hoc or only for simple
problems. For complicated problems, expensive
numerical methods are still the only available
choice, such as the finite element method (Li, 1998,
1999, Li and Chang, 1999), finite difference method
(Du and Qin, 2005), and collocation point method
(Bloor and Wilson, 1990b). In order to improve the
computational efficiency, the Fourier series method
was proposed (Bloor and Wilson, 1996) although it
is effective only when the high frequency modes are
not strongly represented in the boundary conditions.
In addition, another issue to be addressed is that the
existing PDE based approaches only considered
static modeling of surfaces. Dynamic modeling of
curves and surfaces with up to curvature continuities
using analytical PDEs has not been investigated yet.
In this paper, we propose a PDE approach to
tackle both static and dynamic modeling of curves
and surfaces. It represents curves and surfaces
analytically, solves the PDEs quickly and accurately,
and has a capacity to carry out complicated shape
modeling. Therefore, it is applicable to interactive
geometric modeling applications (Ugail et al.,
1999a, 1999b). Unlike the existing PDE-based
methods, which can only generate dynamic surfaces
of tangent continuity, this approach will be able to
generate curves and surfaces of curvature continuity.
2 THEORY AND METHOD
In this section, we introduce two partial differential
equations of motion for static and dynamic modeling
of curves and surfaces, and determine their
composite power series solutions.
2.1 Partial Differential Equations
of Motion
Based on the existing research on dynamic
simulation of cloth deformation (You et al., 1999,
Zhang et al., 1999), deformable moving surfaces
(You and Zhang, 2003), and introducing the
notations of
i
i
u
u
w
w
i
∂
∂
=
,
and
ji
ji
vu
vu
w
w
ji
∂∂
∂
=
+
,
, we use
the following vector-valued fourth and sixth order
partial differential equations of motion for both
static and dynamic modeling of curves and surfaces
Fxxxaxaxa =++++
t
tvvuu
c
,
,,
3
,
2
,
1
24224
ρ (1)
Fx
xxaxaxaxa
=+
++++
t
tvvuvuu
c
,
,,
4
,
3
,
2
,
1
2642246
ρ
(2)
where
u and
v
are parametric variables, t is time
variable,
ρ
is the density, c is the damping
coefficient,
{
}
3~1 ; , ,( === lzyxka
kll
a
for the
fourth order,
4~1 for the sixth order ) are vector-
valued shape control parameters, and the vector-
valued position function
{} zyx , ,=x and vector-
valued force function
{
}
zyx
FFF , ,=F involve
variables
u ,
v
and t , or u and
v
, or u and t , or
u only depending on different modeling tasks of
curves and surfaces.
Because of the introduction of time variable
t ,
Eqs. (1) and (2) integrate both static and dynamic
modeling. When time variable
t in these equations
is taken to be a constant, Eqs. (1) and (2) become
static PDEs and can be used to solve various static
problems of curve and surface modeling.
It is worth pointing out that when time variable
t is set to a constant, Eqs. (1) and (2) actually
represent the generalization of all forms of existing
fourth and sixth order PDEs used for surface
modeling.
Equation (2) provides enough degrees of
freedom to consider not only tangent but also
curvature properties of curves and surfaces at
boundary points or boundary curves. This gives an
advantage in two applications: firstly, it is able to
generate curves and surfaces requiring curvature
continuity; and secondly, the specified curvature
values are useful for shape control and producing
more varieties of different curves and surfaces, since
boundary curvature also has a great influence on
curves and surfaces.
Equations (1) and (2) can be reduced to suit the
modeling of curves, both statically and dynamically.
GRAPP 2011 - International Conference on Computer Graphics Theory and Applications
24

This is undertaken by setting one parametric variable
v
constant.
In order to apply the above equations to static
and dynamic modeling of curves and surfaces, we
must define boundary curves and surface properties
at these curves for surface modeling, and boundary
points and curve properties at these points for curve
modeling. A compound surface may consist of
multiple patches separated by a number of boundary
curves. Similarly, a compound curve can be divided
into a number of segments joined together at the
boundary points. Using Eq. (1), the tangential
properties of surfaces or curves at the boundary
curves or boundary points can be taken into account.
Thus the boundary conditions can be given by
2,1 iuii
uu SxSx === (3)
where
i denotes the index of the boundary curves or
boundary points,
1i
S
and
2 i
S
are the function of
v
and
t for dynamic modeling of surfaces, of
v
for
static modeling of surfaces, of
t for dynamic
modeling of curves, and are constants for static
modeling of curves.
With Eq. (2), higher order derivatives were
introduced which provide more degrees of freedom
to accommodate the curvature property of surfaces
at boundary curves and that of curves at boundary
points. Therefore, boundary conditions for Eq. (2)
are given by
3
,
2,1
2
i
u
iuii
xuu SxSSx ==== (4)
where the definition of
3i
S
is the same as those of
1i
S
and
2 i
S
, and
{
}
)3 2 1( ,,lSSS
ilzilyilxil
==S .
2.2 Solution to PDEs of Motion
Many modeling applications of curves and surfaces
in computer graphics and computer-aided design
such as interactive design and computer animation
require real-time performance. Numerical solutions
of PDEs are too expensive to fulfil this requirement.
Closed form solutions of PDEs, which are the
fastest, are obtainable only for some simple
boundary conditions. In the following, we present a
solution method making use of the composite power
series.
Like the treatment given by You and Zhang
(2004), we first define linearly independent basic
functions as constant 1, parametric variable
v
, time
variable
t , their various elementary functions
excluding polynomials, and their combinations not
in a polynomial form. Then we can decompose the
boundary conditions (3) and (4) into such basic
functions.
To facilitate the description, we also define a
new vector product operator whose operands are two
vectors of the same dimension and each element of
the resultant vector is the product of the
corresponding elements of the two vectors, i. e.,
{
}
zzyyxx
qpqpqp =pq (5)
where
{
}
zyx
ppp =p and
{
}
zyx
qqq =q are two
column vectors.
According to the decomposed linearly
independent basic functions, boundary conditions
(3) and (4) can be rewritten as follows, respectively
0
,
0
ij
J
j
ijuij
J
j
iji
uu scxsbx
∑∑
==
=== (6)
ij
J
j
ij
u
ij
J
j
ijuij
J
j
iji
uu sdxscxsbx
∑∑∑
===
====
0
,
0
,
0
2
(7)
where
{
}
ijzijyijxij
bbb =b ,
{
}
ijzijyijxij
ccc =c and
{
}
ijzijyijxij
ddd =d are the known constants, and
{
}
ijzijyijxij
sss =s are the linearly independent basic
functions which involve the same variables as those
of
)3 2 1( ,,l
il
=S
depending on different modeling
tasks.
The curve or surface to be generated can now be
approximately represented with a composite power
series which combines the power series of the
parametric variable
u with the linearly independent
basic functions
ij
s . Thus the ith curve or surface
segment can be given by
ij
m
J
j
M
m
ijmi
u srx
∑∑
==
=
00
(8)
where
) ,2 ,1 ,0( "=i
ijm
r are the unknown constants
to be determined, and
M
may be set to the same or
different integers for different position function
components and different terms of the same position
function component.
When
1s =
ij
or its some component is 1, the
corresponding
M
should be set to 3 for Eq. (1) and
5 for Eq. (2) because these two equations have been
satisfied for these cases and only the boundary
conditions require to be considered.
Eq. (8) represents the approximate analytical
solution of PDEs (1) and (2) under boundary
conditions (3) and (4). Substituting Eq. (8) into
boundary conditions (6), we determine the unknown
constant
)3 ,2 ,1 ,0 ; , ,2 ,1 ,0( == mJj
ijm
"r . Then
the vector-valued function
i
x
is written in the
following form which satisfies boundary conditions
(3) exactly
A UNIFIED APPROACH TO GEOMETRIC MODELING OF CURVES AND SURFACES
25

[
ij
M
m
ijmi
J
j
jijiijijii
muu srgcbcbgx
⎥
⎦
⎤
+=
∑∑
==
++
40
11
),(),,,,( (9)
where
),,,,(
11 jijiijiji
u
++
cbcbg is the function of
parametric variable
u and the known constants
jiijij 1
, ,
+
bcb and
ji 1+
c . That is
{
}
iki
g=g
and
) , , , ,(
11 jkijkiijkijkikik
cbcbugg
++
= ),,( zyxk = .
),( mu
i
g
is the function of the parametric variable
u and
index
m .
Similarly, substituting Eq. (8) into boundary
conditions (7), the unknown constants
)5 , ,2 ,1 ,0 ; , ,2 ,1 ,0( "" == mJj
ijm
r can be
determined and the vector-valued function
i
x
meeting the boundary conditions (4) accurately is
written as
[
ij
M
m
ijmi
J
j
jijijiijijijii
mu
u
srG
dcbdcbGx
⎥
⎦
⎤
+
=
∑
∑
=
=
+++
6
0
111
),(
),,,,,,(
(10)
Respectively substituting Eq. (9) into (1), and
(10) into (2), we can obtain the residual value
functions of these PDEs. Within the region where
the curve or surface is defined, choosing
N
collocation points and substituting the coordinate
values of these collocation points into the residual
value functions, the residual values at these
collocation points can be written as
BACR −= (11)
By minimizing the squared sum of the residual
values of Eq. (11) using the least squares technique
(You et al. 2000), we obtain the following linear
algebra equations
BAACA
TT
= (12)
The solution of Eq. (12) determines the rest
unknown constants of Eq. (9) or (10). Then curves
or surfaces can be generated from the analytical
mathematical equation (8).
3 COMPUTATIONAL
ACCURACY AND EFFICIENCY
Equations (9) and (10) are analytical expressions.
Although to determine some of the unknown
constants, the least squares technique was employed
for the solution of a very small number of linear
equations, the efficiency is very close to a closed
form solution. Also because we ensure the boundary
conditions are met exactly and errors in the inner
region of the generated curve and surface are
minimized, we can expect to have a good accuracy.
To verify the speculation that the above method
provides both good accuracy and efficiency, in this
section we are undertaking a numerical study.
This study is to make comparisons between the
proposed composite power series solution, finite
difference solution and the corresponding closed
form solution for a specified example where a closed
form solution exists. Firstly, we investigate the error
and efficiency between the proposed solution and
closed form solution for both Eq. (1) and Eq. (2).
Then we compare the efficiency and accuracy of the
three methods only for the static form of Eq. (1). For
a surface, since the determination of
y
x
, and
z
components are the same, we only discuss the x
component. In order to obtain its closed form
solution, the damping term and force function are set
to zero, the density is assumed to be
1= ρ , the
vector-valued parameters are taken to be
1aa ==
21
and
1aa −==
43
, and the boundary conditions have
the form of
tvxxxu
tvxxxu
u
u
u
u
sincos2 1
sincos 0
2
2
,
,
,
,
====
====
(13)
where the derivatives of the second order in the
above equation are redundant for Eq. (1).
The closed form solutions of Eqs. (1) and (2)
subject to the above boundary conditions are
denoted with
x , and the composite power series
solutions and finite difference solutions are
represented with
x
~
. In order to quantify the
difference between these methods, we choose
vu
JI ×
points within the solving region and
introduce the following error equation
∑∑
==
−
×
=
uv
I
i
J
j
ji
jiji
vu
tvux
tvuxtvux
JI
E
11
) ,,(
) ,,(
~
) ,,(
1
(14)
According to the proposed method, we can
obtain the composite power series solutions
x
~
of
this problem for both Eqs. (1) and (2). In this case
study, the collocation points are taken to be 9 for
both equations, and the number of terms of the
composite power series is 5 for Eq. (1) and 7 for Eq.
(2).
Taking the resolution region to be
{
} π ≤≤≤≤ vu 0 ;10 , uniformly choosing 101101×
points within the resolution region, substituting the
values of the two solutions at these points into the
above equation, we find that the relative error
between the closed form solution and the proposed
solution is
3
1037.7
−
×=E for Eq. (1) and
GRAPP 2011 - International Conference on Computer Graphics Theory and Applications
26

4
1005.1
−
×=E for Eq. (2). Clearly, these errors are
very small.
The computational efficiency of the proposed
method is also very high. We have timed the process
determining the unknown constants in the closed
form solutions and composite power series solutions.
It was found that both methods took less than
6
10
−
second on an ordinary PC to solve Eqs. (1) and (2).
In order to further demonstrate good accuracy
and efficiency of proposed composite power series
method, in the following, we carry out the finite
difference calculation of Eq. (1) subject to boundary
conditions. For simplicity, we only study the static
problem of the above example, i. e., set
1sin =t in
the boundary conditions (13), neglect the force
function and all other terms containing the partial
derivatives with respect to the time variable
t in Eq.
(1), and take the resolution region to be
{} 10 ;10 ≤≤≤≤ vu . The collocation points and terms
of the proposed composite power series are the same
as above. The boundary conditions for the finite
difference calculation are taken from the closed from
solution of the same problem. Within the resolution
region, uniformly set
vu
NN ×
nodes, and determine
the values of
x component at these nodes using the
finite difference formulae of Eq. (1) and all the
boundary conditions of this problem. Then calculate
the values of the proposed power series solution and
closed form solution at these nodes, and use Eq. (14)
to find the errors among them. In Table 1, PS means
the errors between the proposed power series
solution and the closed form solution, FD stands for
the errors between the finite difference solution and
the closed form solution, and the last row of the
table gives the time of the finite difference solution.
The time of the proposed solution and closed form
solution is less than
6
10
−
second once again.
Table 1: Comparison of accuracy and efficiency.
vu
NN ×
1515
× 2525 × 3535 ×
PS
0.00437 0.0045 0.00455
FD
0.738 0.622 0.579
Time(seconds)
08.3 4 5.71 78.573
It is very clear that the proposed method has much
better computational accuracy and efficiency than
the finite difference method. Although the total
number of the nodes was greatly increased leading
to very expensive computational cost, the
computational accuracy of the finite difference
method was not improved obviously. From the
tendency of the computational errors given by the
finite difference method, it appears difficult to reach
as high accuracy as that of the composite power
series solution although we increase the nodes for
the finite difference calculation. Low computational
efficiency of numerical methods indicates they are
less ideal for the computer graphics applications
requiring real-time performance.
In summary, the proposed composite power
series solution is both accurate and efficient. It can
generate surfaces with the similar efficiency and
accuracy to the closed form solution method, far
more quickly and accurately than numerical
methods.
The proposed method can be employed to a wide
range of shape modeling applications. In the
following, we will apply this method to solve a
number of dynamic and static modeling problems of
curves and surfaces.
4 DYNAMIC MODELLING
Dynamic modeling of curves and surfaces is a very
interesting subject of computer animation. With the
developed composite power series method based on
Eqs. (1) and (2) together with boundary conditions
(3) and (4), we can perform dynamic modeling of
curves and surfaces analytically.
4.1 Dynamic Surface Modeling
For dynamic surface modeling, we here give an
example to show how an original surface is
consecutively changed to a series of different
surfaces using Eq. (1). The boundary conditions for
this dynamic modeling are
{} {} { }
{} {} { }
{}
{}{}
{}
{} {}
{} {} {}
{} {} 00
12cos)1(2sin
12sin)1(2cos
1
10sin
12cos2sin)2(
12sin2cos)23(
0
,
2
4433,
4433,
1100,
2
2211,
2211,
=
−
′
+
′
=
−
′
+
′
=
=
′
+
′
=
′
+−
′
=
′
+−
′
=
=
u
u
u
u
u
u
zz
vtrrvrryy
vtrrvrrxx
u
vthhhhzz
vtrrvtrryy
vtrrvtrrxx
u
ππ
ππ
π
ππ
ππ
(15)
From the above boundary conditions, we can
obtain the linearly independent basic functions
v π 2cos , vt π 2cos , v π 12sin , vt π 12sin for x
component,
v π 2sin , vt π 2sin , v π 12cos , vt π 12cos
2
A UNIFIED APPROACH TO GEOMETRIC MODELING OF CURVES AND SURFACES
27

for
y
component, and 1 and vt π 10sin for
z
components. According to these linearly
independent basic functions, we can construct the
following composite power series functions
vtururz
v
turvur
vturvury
vturvur
vturvurx
M
m
m
mz
m
m
mz
M
m
m
my
M
m
m
my
M
m
m
my
M
m
m
my
M
m
m
mx
M
m
m
mx
M
m
m
mx
M
m
m
mx
π
π
π
ππ
ππ
ππ
10sin
12cos
12cos
2sin2sin
12sin12sin
2cos2cos
0
01
3
0
00
2
0
03
0
02
0
01
0
00
0
03
0
02
0
01
0
00
∑∑
∑∑
∑∑
∑∑
∑∑
==
==
==
==
==
+=
++
+=
++
+=
(16)
The unknown constants
3~0(
0
=jr
jmk
for x and
y components and j=0,1 for z component;
) ;30 zy,x,k~m == in the above equation can be
determined from boundary conditions (15). Then
substituting Eq. (16) into (1), uniformly choosing 9
collocation points within the solving region and
taking 6 terms for each composite power series
which means only 2 unknown constants in Eq. (12)
are to be determined, we can obtain the rest
unknown constants and analytical mathematical
equations of the surface to be created. Specifying the
values of the geometric parameters in Eq. (15) and
vector-valued parameters in Eq. (1), we can generate
the surface at any time
t .
t = 0 t = 0.25
t = 0.5 t = 0.75 t =1
Figure 1: Dynamic modeling of a surface.
In Figure 1, we give the images of the surface at
t=0, 0.25, 0.5, 0.75 and 1. They were created with
one surface patch determined by the analytical
mathematical equations. This example indicates that
the proposed composite power series method can be
used to animate objects directly such as skin
deformation of the arms and legs during human
motion, or produce a series of key frames of the
object to be animated.
4.2 Dynamic Curve Modeling
When the parametric variable
v
in Eqs. (1) and (2)
together with boundary conditions (3) and (4) is
taken to be a constant, we can carry out dynamic
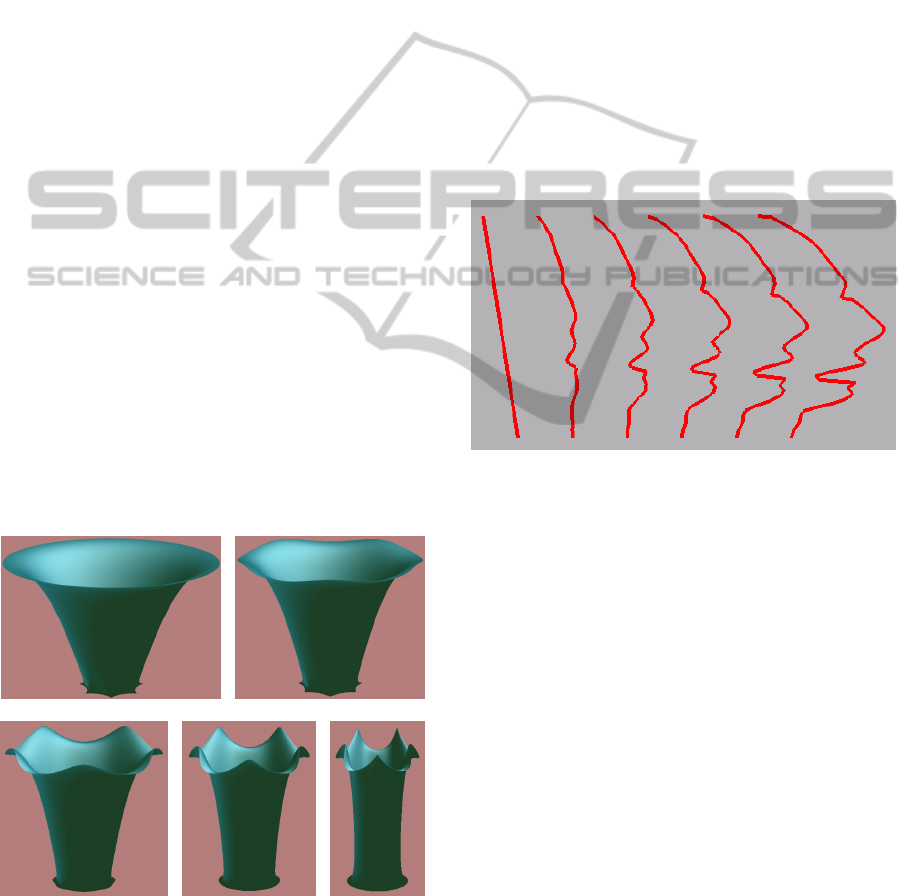
modeling of curves. In Figure 2, we give an example
to show how a straight line is consecutively changed
to a human face profile which consists of four curve
segments with each segment being determined by a
vector-valued position function.
Figure 2: Dynamic modeling of a curve.
5 STATIC MODELING
When the time variable t in Eqs. (1)-(4) is set to a
constant, these equations can be applied to perform
static modeling of curves and surfaces. In the
following, we will give some examples to indicate
the applications of these equations in free-form
surface generation and surface blending.
5.1 Free-form Surface Generation
The proposed method is also an effective means for
free-form surface generation. Rather than moving
the control points, the surfaces to be generated can
be controlled and deformed simply by changing
some parameters, such as the vector-valued shape
control parameters, tangential and curvature
boundary conditions as well as the force function.
Since any complicated boundary curves, planar or
spatial, can always be represented by mathematical
functions, a surface so defined can be created with
GRAPP 2011 - International Conference on Computer Graphics Theory and Applications
28

the proposed method.
By dividing the object to be created into some
surface patches connected by the boundary curves,
we can generate complicated free-form surfaces. In
Figure 3, the surfaces of a fish were created with the
proposed composite power series method.
Figure 3: Surface generation of a fish.
5.2 Surface Blending
Surface blending is another important area of surface
modeling. Here we give an example to illustrate the
application of the proposed method.
This example is to blend two intersecting
cylinders using the solution of the static form of Eq.
(1) under boundary conditions (3). We only employ
18 collocation points in the blending region and 6
terms for each composite power series. The obtained
blending surface is given in Figure 4. The whole
resolution process took less than
6
10
−
second.
Figure 4: Blending between two intersecting cylinders.
6 CONCLUSIONS
In this paper, we have proposed a unified curve and
surface modeling approach so that both static and
dynamic problems can be represented in a uniform
manner. This approach is based on the use of two
partial differential equations of motion, a vector-
valued fourth order PDE and a vector-valued sixth
order PDE. The former is able to satisfy tangent
boundary conditions, while the latter is able to meet
curvature conditions.
A key element of making the proposed approach
applicable to interactive graphics applications is to
solve these PDEs efficiently and effectively. To this
point, we have used a composite power series
method, which is able to give analytical
mathematical equations of curves and surfaces to be
created. The positional, tangential and curvature
functions in the boundary conditions were firstly
decomposed into a number of linearly independent
basic functions which combine with the power series
of another parametric variable to formulate
approximate solution functions. By determining
some unknown constants in these solution functions,
the boundary conditions are always exactly satisfied.
The residual values in the proposed PDEs are
minimized using the least squares technique which
further reduces the discrepancy between the
approximate and the accurate shapes.
The computational accuracy and efficiency of
the proposed composite power series method have
been investigated. The comparisons between this
research, the finite difference approach and the
closed form solution indicate that the proposed
method can generate surfaces with similar efficiency
and accuracy to the closed form solution method,
and far more quickly and accurately than numerical
methods.
The proposed partial differential equations can
also be degenerated for the purpose of curve
modeling in a unified format. Since curve modeling
is more flexible, it is useful in complex surface
modeling as well.
To demonstrate its applications, we have applied
this approach to a number of examples of static and
dynamic modeling of curves and surfaces.
REFERENCES
Athanasopoulos, M., Ugail, H., Castro, G. G., 2009,
Parametric design of aircraft geometry using partial
differential equations. Advances in Engineering
Software 40, 479–486.
A UNIFIED APPROACH TO GEOMETRIC MODELING OF CURVES AND SURFACES
29

Bloor, M. I. G., Wilson, M. J., 1989a. Generating n-sided
patches with partial differential equations. New
Advances in Computer Graphics, Proceedings of CG
International’89, Springer-Verlag, Tokyo, Japan, 129-
145.
Bloor, M. I. G., Wilson, M. J., 1989b. Generating blend
surfaces using partial differential equations.
Computer-Aided Design 21(3),165-171.
Bloor, M. I. G., Wilson, M. J., 1990a. Using partial
differential equations to generate free-form surfaces.
Computer-Aided Design 22(4), 202-212.
Bloor, M. I. G., Wilson, M. J., 1990b. Representing PDE
surfaces in terms of B-splines. Computer-Aided
Design 22(6), 324-331.
Bloor, M. I. G., Wilson, M. J., 1996. Spectral
approximations to PDE surfaces, Computer-Aided
design 28(2),145-152.
Celniker, G., Gossard, D., 1991. Deformable curve and
surface finite-elements for free-form shape design.
Computer Graphics 25(4), 257-266.
Du, H., Qin, H., 2005. Dynamic PDE-based surface design
using geometric and physical constraints. Graphical
Models 67, 43–71.
Farin, G., 1997. Curves and Surfaces for Computer Aided
Geometric Design: A Practical Guide. 4th Edition,
Academic Press.
Guillet, S., Léon, J. C., 1998. Parametrically deformed
free-form surfaces as part of a variational model.
Computer-Aided Design 30(8), 621-630.
Hyodo, Y., 1990. The generation of free form surface
defined with contour and sectional curves. Journal of
the Japan Society of Precision Engineering 56(10),
1912-1916.
Li, Z. C., 1998. Boundary penalty finite element methods
for blending surfaces, I. Basic theory. Journal of
Computational Mathematics 16, 457-480.
Li, Z. C., 1999. Boundary penalty finite element methods
for blending surfaces, II. Biharmonic equations.
Journal of Computational and Applied Mathematics
110, 155-176.
Li, Z. C., Chang, C.-S., 1999. Boundary penalty finite
element methods for blending surfaces, III.
Superconvergence and stability and examples. Journal
of Computational and Applied Mathematics 110, 241-
270.
Miura, K. T., 2000. Unit quaternion integral curve: a new
type of fair free-form curves. Computer Aided
Geometric Design 17(1), 39-58.
Nealen, A., Müller, M., Keiser, R., Boxerman, E., Carlson,
M., 2006. Physically based deformable models in
computer graphics. Computer Graphics Forum 25(4),
809-836.
Ochiai, Y., Yasutomi, Z., 2000. Improved method
generating a free-form surface using integral
equations. Computer Aided Geometric Design 17(3),
233-245.
Qin, H., Terzopoulos, D., 1995. Dynamic NURBS swung
surfaces for physics-based shape design. Computer-
aided Design 27(2), 111-127.
Terzopoulos, D., Platt, J., Barr, A., Fleischer, K., 1987.
Elastically deformable models. Computer Graphics
21(4), 205-214.
Terzopoulos, D., Fleischer, K., 1988. Modeling inelastic
deformation: viscoelasticity, plasticity, fracture.
Computer Graphics 22(4), 269-278.
Terzopoulos, D., Qin, H., 1994. Dynamic NURBS with
geometric constraints for interactive sculpting. ACM
Transactions on Graphics 13(2), 103-136.
Ugail, H., Bloor, M. I. G., Wilson, M. J., 1999a.
Techniques for interactive design using the PDE
method. ACM Transactions on Graphics 18(2), 195-
212.
Ugail, H., Bloor, M. I. G., Wilson, M. J., 1999b.
Manipulation of PDE surfaces using an interactively
defined parameterisation. Computers & Graphics
23(4), 525-534.
Vassilev, T. I., 1997. Interactive sculpting with
deformable nonuniform B-splines. Computer Graphics
Forum 16, 191-199.
Vida, J., Martin, R. R., Varady, T., 1994. A survey of
blending methods that use parametric surfaces.
Computer-Aided Design 26(5), 341-365.
You, L. H., Zhang, J. J., Comninos, P., 1999. Cloth
deformation modelling using a plate bending model.
In Proceedings of the 7
th
International Conference in
Central Europo on Computer Graphics, Visualization
and Interactive Digital Media’99, 485-491.
You, L. H., Zhang, J. J., Comninos, P., 2000. A volumetric
deformable muscle model for computer animation
using weighted residual method. Computer Methods in
Applied Mechanics and Engineering 190(8-10), 853-
863.
You, L. H., Zhang, J. J., 2003. Fast generation of 3-D
deformable moving surfaces. IEEE Transactions on
Systems, Man and Cybernetics-Part B: Cybernetics
33(4), 616-625.
You, L. H., Zhang, J. J., 2004. PDE blending surfaces with
2
C continuity. Computers & Graphics 28, 895-906.
Zhang, J. J., You, L. H., Comninos, P., 1999. Computer
simulation of flexible fabrics. In Proceedings of the
17
th
Annual Conference, UK Chapter,
EUROGRAPHICS, 27-35.
GRAPP 2011 - International Conference on Computer Graphics Theory and Applications
30