
MULTI-CAMERA PEOPLE TRACKING WITH HIERARCHICAL
LIKELIHOOD GRIDS
Lili Chen, Giorgio Panin and Alois Knoll
Fakult
¨
at f
¨
ur Informatik, Technische Universit
¨
at M
¨
unchen, Boltzmannstrasse 3, 85748 Garching bei M
¨
unchen, Germany
Keywords:
Edge-based background subtraction, Hierarchical likelihood grids, Oriented distance transform, Data associa-
tion, Multi-view and Multi-target tracking.
Abstract:
In this paper, we present a grid-based tracking by detection methodology, applied to 3D people tracking for
multi-camera video surveillance. In particular, frame-by-frame detection is performed by means of hierar-
chical likelihood grids, using edge matching through the oriented distance transform on each camera view
and a simple person model, followed by likelihood grids clustering in state-space. Subsequently, the tracking
module performs a global nearest neighbor data association, in order to initiate, maintain and terminate tracks
automatically. The proposed system can easily include additional features, such as color or background sub-
traction, it can be scaled to more camera views, and it can be used to track other items as well. We demonstrate
it through experiments in indoor sequences, using a calibrated multi-camera setup.
1 INTRODUCTION
Nowadays automatic visual surveillance is becoming
increasingly popular, because of its wide applications
in indoor and outdoor environments with security re-
quirements. Usually there are two major problems
in an automatic surveillance system: one is to detect
moving targets, and the other is to keep them tracked
throughout the sequence. As the most representa-
tive application, detecting and tracking people is ob-
viously the most challenging and attractive topic, due
to people’s huge variations in physical appearance,
pose, movement and interaction. Therefore, people
detection and tracking receives a significant amount
of attention in the area of research and development.
Although some systems have been successfully
developed towards this challenging task, it still re-
mains difficult to detect and track multiple people pre-
cisely and automatically, only using generic models
in a cluttered scene. This paper addresses the prob-
lem of employing a grid-based tracking-by-detection
methodology, with a very simple shape model. The
primary goal of our paper is to develop a fully auto-
matic system for tracking multiple people in an over-
lapping, multi-camera environment, providing a 3D
output robust to mutual occlusion between interacting
people.
As a commonly used technique for segmenting
out objects of interest, background subtraction has
achieved a significant success in fixed camera scenar-
ios. Most of the methods work by comparing color
or intensities of pixels in the incoming video frame
to the reference image (Stauffer and Grimson, 2000;
Wren et al., 1997; Eng et al., 2004). However, it
has the drawback of being susceptible to illumination
changes, and provides a less precise localization. In
contrast, we propose here an edge-based background
subtraction, which employs the Canny edge map to-
gether with Sobel gradients, because edges are more
precisely and stably localized, to a better extent in
presence of illumination changes, so that the model
has not to be adapted so often.
A second contribution of our system is frame-by-
frame detection by means of hierarchical likelihood
grids. This scheme, adapted from (Stenger et al.,
2006), takes the advantage of multi-resolution grids
that can, precisely and efficiently locate targets in
cluttered scenes, without prior knowledge of their po-
sition. In particular, we compute the likelihood by
edge matching through the oriented distance trans-
form, which matches not only the location of edge
points but also their orientation. And the likelihood
is first computed on a coarse grid, then refined on
the next level only the locations where likelihoods
are higher than a given threshold. Subsequently, we
perform state-space clustering on the high-resolution
grid, in order to find the relevant peaks, possibly as-
sociated to people.
474
Chen L., Panin G. and Knoll A..
MULTI-CAMERA PEOPLE TRACKING WITH HIERARCHICAL LIKELIHOOD GRIDS.
DOI: 10.5220/0003316904740483
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2011), pages 474-483
ISBN: 978-989-8425-47-8
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

The third main issue consists in associating de-
tected peaks to tracks, which is a classical data as-
sociation problem, where a track can be updated by at
most one measurement, and a measurement can be
assigned to at most one track. Several approaches
have been developed for this purpose, the most rep-
resentative ones being (Fortmann et al., 1983; Reid,
1979); however, in place of complex methods, which
require more complex models and parameter tuning,
and further increase the computational complexity,
our tracking module employs a Global Nearest Neigh-
bor (GNN) approach in order to initiate, maintain and
terminate tracks automatically.
The remainder of the paper is organized as fol-
lows: Section 2 reviews the state of the art and related
work to our paper. Section 3 describes the general
system overview with hardware setup and algorith-
mic flow of software. In Section 4, we provide the
detailed detection procedure, including models, edge-
based background subtraction, hierarchical grid eval-
uation as well as model-based contour matching and
state-space clustering. Tracking by data association is
presented in Section 5. The experimental results are
discussed in Section 6. Finally, Section 7 summarizes
the paper and proposes future development roads.
2 RELATED WORK
A vast amount of literature has been published on
people detection and tracking. We can mainly clas-
sify it into four categories: region-based approaches,
which are based on the variation of image regions
in motion (Khan et al., 2001); feature-based (Wren
et al., 1997; Fieguth and Terzopoulos, 1997; Li et al.,
2003), that usually utilize information about color,
texture, etc.; contour-based (Isard and Blake, 1996;
Nguyen et al., 2002; Roh et al., 2007), that make use
of the bounding contours to represent the target out-
line; and model-based methods (Gavrila and Davis,
1996; Andriluka et al., 2010) that explicitly require
a 2D or 3D model of a person for tracking. How-
ever, a too detailed review of all the approaches is
beyond the scope of our paper, therefore, in the fol-
lowing we will focus on people tracking-by-detection
methodologies, more related to our work. There has
been a number of literature on this approach (Okuma
et al., 2004; Leibe et al., 2007; Wu and Nevatia,
2007), where detection of people in individual frame,
as well as data association between detections in dif-
ferent frames, are the most challenging and ambigu-
ous issues(Andriluka et al., 2008).
Template-based methods have yielded nice results
for locating targets with no prior knowledge in a clut-
tered scene. In (Gavrila, 2000), the efficiency of this
method is illustrated, by using about 4,500 templates
to match pedestrians in images. The core is the idea
of using a Chamfer distance measure, so that match-
ing a template with the DT image results in a similar-
ity measure, that is a smooth function of the template
transformation parameters. Meanwhile this approach
enables the use of an efficient search algorithm that
locks onto the correct solution. However, if only com-
puting the location of edge pixels without considering
their orientation when computing distance transform,
it inevitably leads to a high rate of false alarms in pres-
ence of clutter.
Another highlight of this system is the utiliza-
tion of a template hierarchy, which is generated au-
tomatically from available examples, and formed by
a bottom-up approach, using a partitioned clustering
algorithm. It only searches locations where the dis-
tance measure is under a given threshold, so that a
speed-up of three orders of magnitude, compared to
exhaustive searching, is demonstrated.
This idea was taken further by (Stenger et al.,
2006), that however does not build the template hi-
erarchy (or tree) by bottom-up clustering, rather by
partitioning a state-space represented with an inte-
gral grid. The grid is hierarchically partitioned as the
search descends into each region, so that regions at
the leaf-level define the finest partition. This method
is demonstrated to be capable of covering 3D mo-
tion, even with self-occlusion. Unfortunately, both
approaches need a very specific model, only valid for
a specific target.
Once the measurements have been obtained from
the frame-by-frame detection, data association can
be applied to solve the problem of measurement
to track assignment. A simple nearest-neighbor
approach(Bar-Shalom and Fortmann, 1988) uses only
the closest observation to any predicted state in order
to perform the measurement update, and it is com-
monly used for MTT systems because of its fast com-
putation. More complex approaches, such as Joint
Probabilistic Data Association Filter (JPDA) (Fort-
mann et al., 1983) and Multiple Hypothesis Tracking
(MHT) (Reid, 1979) solve this problem by maintain-
ing multiple hypotheses, until enough measurements
can be collected to resolve the ambiguity. In partic-
ular, (Fortmann et al., 1983) combines all of the po-
tential measurements into one weighted average, be-
fore associating it to the track, in a single update. By
contrast, (Reid, 1979) calculates every possible up-
date hypothesis, with a track, formed by previous hy-
potheses associated to the target. Both methods are
known to be quite complex, and require a careful im-
plementation in terms of parameters; in particular, the
MULTI-CAMERA PEOPLE TRACKING WITH HIERARCHICAL LIKELIHOOD GRIDS
475
latter cannot avoid the drawback of an exponentially
growing computational complexity, with the number
of targets and measurements involved in the resolu-
tion situation, so that sub-optimal solutions must be
sought (Cox and Hingorani, 1996).
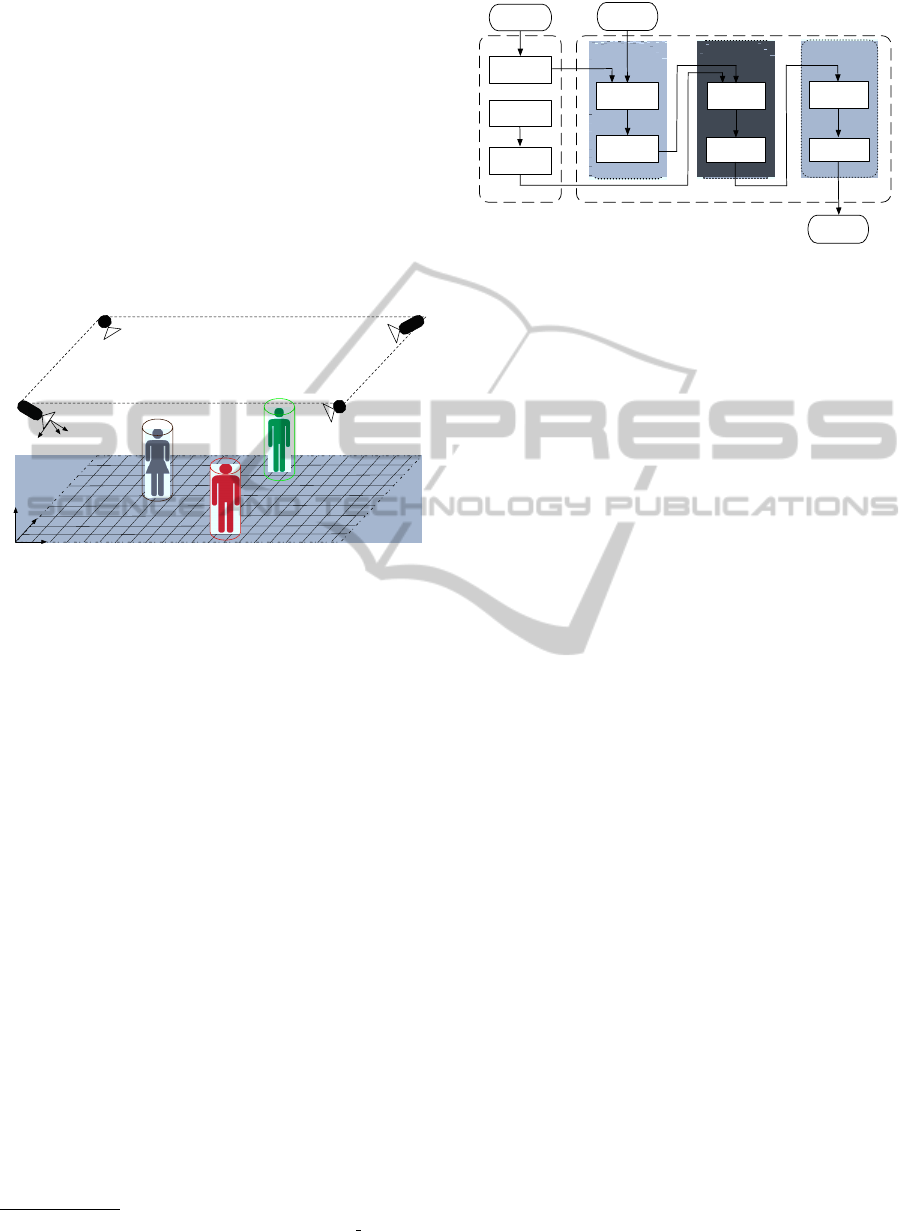
3 SYSTEM OVERVIEW
In this section, we describe the hardware setup and
present an overview of our tracking system, which
will be discussed in more detail afterwards.
X
Y
Z
World Coordinate
Camera Coordinate
XY
Z
4 Cameras on Ceiling
Scene
Figure 1: Hardware setup.
The overall setup is depicted in Figure 1. Four
uEye usb cameras, with a resolution of 752 ×480, are
mounted overhead on the corners of the ceiling, each
of them observing the same 3D scene synchronously
from different viewpoints. Furthermore, all the four
cameras are connected to one multi-core PC. A nec-
essary step before being able to get accurate 3D in-
formation, is calibration of the intrinsic and extrinsic
camera parameters, that we perform with the Matlab
Calibration Toolbox
1
, with respect to a world coordi-
nates system placed on the floor.
The detection and tracking software is designed
and implemented in the OpenTL framework
2
(Panin
et al., 2008; Panin, 2011), which is a structured,
general purpose architecture for model-based visual
tracking. We provide the block diagram of our track-
ing system in Figure 2, that consists of two main pro-
cessing modules. Offline, we use a certain number
of background frames to learn the background model.
Moreover, grid states are sampled for each level, and
the silhouettes are generated by projecting the exter-
nal contours of the cylinder shape and keeping, for
each contour and each camera view, a list of pixel
positions and normals. Online, we have three main
sub-modules: pre-process, detection and tracking.
1
http://www.vision.caltech.edu/bouguetj/calib doc/
2
http://www.opentl.org
Background
learning
Generate
silhouettes
Likelihood
computing
Clustering in
state space
Data
association
OFFLINE
TRACKING
ONLINE
Tracked
Result
Background
subtraction
Compute
OrientedDT
PRE_PROCESS
Background
frames
Sample
grid states
DETECTION
Track
maintenance
Input video
Figure 2: Block diagram of the tracking system.
In the pre-process part, for each camera view fore-
ground contours are segmented by edge-based back-
ground subtraction, using the learned model. After-
wards, we compute an oriented distance transform
onto this image, in order to match, for each tem-
plate, both the location and the orientation of its con-
tours. In particular, the oriented DT is efficiently com-
puted over a finite set of orientations, so that the im-
age is sampled over parallel scan lines that are pre-
computed. The advantage of using both edge posi-
tion and orientation, during background subtraction
as well as template matching, is a strong reduction of
false alarms, i.e. false edge matching, that would arise
when using only positional information.
Detection part first computes the likelihoods by
matching projected templates and oriented DT for
each camera view, where the likelihoods are com-
puted on the coarse grid firstly, then refined on the
next resolution only the locations where the likeli-
hood is higher than a given threshold, the joint likeli-
hoods can simply be multiplied then. The object-level
measurements, or target hypotheses, are obtained by
means of likelihood grid clustering, that is performed
by Gaussian filtering of the high-resolution grid, and
local maxima detection. Finally, the tracking module
performs measurement-to-target association with the
Global Nearest Neighbor approach, in order to initi-
ate, maintain and terminate tracks automatically.
4 PEOPLE DETECTION
In this section, we provide more details about peo-
ple detection, that serves as one of our key building
blocks for our system.
4.1 Construction of Template Hierarchy
The idea to construct a template hierarchy is inspired
by the paper (Stenger et al., 2006), as well as by
the system developed by (Gavrila, 2000), extended
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
476
to multiple views, multiple targets, and with a more
general template.
Assuming there are L levels of search, the state
space is partitioned with a coarse-to-fine strategy. A
graphical illustration is shown in Figure 3.
Figure 3: Grid based state space with hierarchical partition.
Each discrete region
R
i,l
N
l
i=1
, where N
l
is the
number of cells at level l, is sampled at its center, be-
fore the template hierarchy is generated. Meanwhile,
we connect regions at a child level with its parent cell,
by computing the nearest-neighbor in state-space, as
well as its nearest neighbors within the same level, as
it will be described in Section 4.4, in order to smooth
the grid likelihoods.
After sampling the grid, templates are generated
by rendering the 3D model at each state, under the re-
spective camera projection. The model chosen in our
approach is a simple cylinder, undergoing (x,y) trans-
lation on the floor, while its silhouette is generated by
projecting the external contour. An example is shown
in Figure 4, while a partial view of the hierarchy of
silhouettes is depicted in Figure 5.
(a) (b) (c)
Figure 4: Our model. (a) Discretized cylinder. (b) Projected
external contour. (c) Silhouette with normals.
For each silhouette, the position of each point as
well as its normal are collected, as it will be described
further in Section 4.3. As already emphasized, both
grid sampling and template hierarchy generation are
performed offline.
Figure 5: Hierarchy with silhouette of cylinder.
4.2 Background Learning and
Foreground Segmentation
In order to match the image data with the templates,
we first apply an edge-based background subtraction.
This approach can be divided into two phases:
background learning (offline) and foreground seg-
mentation (online). In the first phase, we utilize a cer-
tain number N of frames without people, in order to
learn the background model. Let Θ
b
(t), G
bx
(t), G
by
(t)
respectively be the Canny edge map, and Sobel x-
gradient and y-gradient images, detected at frame
I
b
(t). The Canny map Θ
b
is accumulated by bi-
nary OR, from frame Θ
(I)
b
(1), . . . , Θ
(I)
b
(N), while So-
bel gradients are accumulated in a running average
over the same frames. At the end, we normalize the
accumulated Sobel image
G
2
bx
+ G
2
by
= 1, ∀(x, y) (1)
Subsequently, standard distance transform is applied
to the accumulated background Canny map, and
thresholded to a few pixels, providing a binary mask
Θ
DT
∈
{
0, 1
}
, where potential background edges are
found.
Online, from the foreground Canny map and So-
bel gradients Θ
f
(t), G
f x
(t), G
f y
(t) of camera frame
I
f
(t), we test the position and orientation of each edge
pixel: edges Θ
f
(t) 6= 0 that lie near to a background
edge Θ
DT
6= 0 are candidate for removal.
Then, we further test these edges for orientation
with the Sobel masks, and if the scalar product is
higher than another threshold θ
G
bx
G
f x
+ G
by
G
f y
q
G
2
f x
+ G
2
f y
> θ (2)
the point is removed from Θ
f
(t). Figure 6 shows an
example of this procedure: as we can see, the result-
MULTI-CAMERA PEOPLE TRACKING WITH HIERARCHICAL LIKELIHOOD GRIDS
477

(a) (b) (c) (d)
Figure 6: Edge-based background subtraction. (a) Original frame. (b) Learned background model. (c) Unsegmented fore-
ground edge. (d) Segmented foreground edge.
ing edge map robustly preserves the person contours,
while discarding most of the background edges.
4.3 Matching based on the Oriented
Distance Transform
The next step is to match foreground edges with the
model silhouettes. One possibility would be to use
the Chamfer distance transform on the edge map,
that is tolerant to small shape variations, and has al-
ready been applied in several works, such as (Borge-
fors, 1988; Gavrila, 2000). However, in case of im-
ages with considerable clutter, a significant rate of
false alarms would be present. This problem can be
reduced by matching not only the location of edge
points, but also their orientation (Olsen and Hutten-
locher, 1997).
Therefore, we propose here another approach, us-
ing the oriented distance transform. We define the
oriented DT by scanning the edge image along par-
allel lines L
γ
(a) through pixel a = (x, y) for a given
orientation γ, and repeat it for a finite set of N
γ
di-
rections Γ =
{
γ
i
}
N
γ
i=1
. The algorithm is illustrated in
Figure 7.
Figure 7: Scanning single line for one direction. From left
to right: Multiple single line scanning; Distance value to the
nearest edge point on the line; Multiple scanning directions.
In particular, for each direction and each scan
line, the oriented DT is a mono-dimensional function,
looking for the nearest edge point b on either direction
b = DT
γ
(a) = min
b∈L
γ
(a)
k
a − b
k
(3)
An example of oriented distance transform is shown
in Figure 8.
Once oriented DTs are computed, template match-
ing simply amounts to compute the likelihood, by
summing up all values over the silhouette pixels, in
the corresponding direction of the normal. To formal-
ize the idea, a projected template s is represented by
a set of pixel positions and normals
{
x
i
, y
i
, g
i
}
N
i=1
, ob-
tained by re-projection through a 3 × 4 camera pro-
jection matrix P, where g
i
selects the nearest γ ∈ Γ,
from which the DT value will be taken. Therefore,
the likelihood for state hypothesis s is given by:
P(z|s) = exp
−
1
2NR
2
N
∑
i=1
min
DT
γ(g
i
)
(x
i
, y
i
)
2
, D
2
max
!
(4)
where γ(g
i
) denotes the closest available direction to
the normal, and the sum is performed over all val-
ues
{
x
i
, y
i
, g
i
}
N
i=1
. R is the measurement standard de-
viation, and an outlier threshold is usually fixed at
D
max
= 3R, which is our validation gate for a more
robust matching. Also notice that, in order to avoid
problems with different scales, the sum is further nor-
malized by N.
During the computation of likelihood, a coarse-to-
fine search strategy is applied by evaluating it, at each
level, only for locations where the parent cell likeli-
hood is higher than a given threshold, which is usu-
ally obtained as the average likelihood (Stenger et al.,
2006). For those cells where the parent likelihood is
under the threshold, its value is simply inherited, thus
saving a large amount of computation.
4.4 Likelihood Grid Clustering
In order to obtain the object-level measurements, or
target hypotheses, after likelihood computation we
employ a clustering procedure on the high-resolution
grid, where each cluster is a local maximum, poten-
tially corresponding to a person.
This approach is similar to mean-shift, but explic-
itly done on discrete states. First of all, a Gaussian
filtering is applied to the grid, where the isotropic
Gaussian corresponds to the filtering kernel. For each
cell s
i
within the grid, we take the nearest neighbor
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
478

(a) (b)
(c)
Figure 8: Results of oriented distance transform. (a) Input
image. (b) Foreground edge map. (c) Oriented DT (at 12
discrete orientations).
s
j
by looking at the connected states with distance
d
i, j
=
s
i
− s
j
up to a validation gate D
max
= 3σ
2
s
,
where σ
2
s
is the measurement covariance in state-
space, these neighbors are pre-computed in the off-
line phase. For each neighbor, the Gaussian weight is
also pre-computed by
W
i, j
= exp(−
d
2
i, j
2σ
2
s
) (5)
the computed weights are also normalized to 1, so that
the smoothed likelihood for state cell s
i
is given by
P(z|s)
weighted
(i) =
∑
i, j
W
i, j
· P(z|s)( j) (6)
Subsequently, local maxima are detected (within
the same neighborhood), to obtain the target hypothe-
ses, or measurements. The final step will be to asso-
ciate these hypotheses to tracks, as it will be described
in next section.
5 MULTIPLE PEOPLE
TRACKING
In this section we deal with the problem of multi-
target tracking, by associating measurements ob-
tained from our detector to individual tracks, also per-
forming automatic track initiation and termination.
In particular, our track management follows a
strategy indicated in (Bar-Shalom and Li, 1995):
• Track Initiation. In case of new targets entering
into the scene, they will generate measurements
that are too far from the existing targets, and there-
fore can be used to start new tracks. In this case,
they are labeled with a unique ID, and a counter
for the number of consecutive, successful detec-
tions for this target is also initialized to 1.
• Track Maintenance. During tracking, a target is
successfully detected whenever the data associ-
ation algorithm provides one valid measurement
for it, so its counter is increased up to a maxi-
mum value (which can be taken as a confirma-
tion time), while in case of misdetection it will
be decreased. Those targets which are success-
fully detected over the confirmation time, can be
considered as stable targets and maintained by the
algorithm. In this way, if a target is misdetected
for a few frames in case of occlusion, it can still
be recovered until the counter goes to 0.
• Track Termination. When a target exits the scene,
or after occlusion for a too long time, its misdetec-
tion counter goes to 0, and its track is terminated.
A pseudo-code of the whole procedure is shown
in Algorithm 1, where the GNN algorithm is called in
(line 25).
The data association problem consists in decid-
ing which measurement should correspond to which
track. Although our detection algorithm is fairly ro-
bust, it is also not person-specific, and therefore in a
small indoor environment there are always ambigui-
ties, arising from neighboring targets, as well as from
missing detections and false alarms caused by back-
ground clutter. To this respect we employ the Global
Nearest Neighbor (GNN) approach, that gives a good
solution for this problem (Konstantinova et al., 2003),
while requiring relative low computational cost.
The first step of the GNN is to set up a distance
(or cost) matrix: assuming that, at time t, there are M
existing tracks and N measurements, the cost matrix
is given by
D =
d
11
d
12
··· d
1N
d
21
d
22
··· d
2N
.
.
.
.
.
.
.
.
.
.
.
.
d
M1
d
M2
··· d
MN
(7)
where d
i j
is the Euclidean distance between track
i and measurement j, and i = 1, 2, . . . , M; j =
1, 2, . . . , N. In particular, d
i j
is set to ∞ if it exceeds
the validation gate, which is a circle with fixed radius
around the predicted position, eliminating unlikely
observation-to-track pairs. Moreover, it is commonly
required that a target can be associated with at most
one measurement (none, in case of misdetection), and
MULTI-CAMERA PEOPLE TRACKING WITH HIERARCHICAL LIKELIHOOD GRIDS
479

a measurement can be associated to at most one target
(none, in case of false alarms).
The GNN solution to this problem is the one that
maximizes the number of valid assignments, while
minimizing the sum of distances of the assigned pairs.
To this aim, we adopt the extended Munkres’ algo-
rithm (Burgeois and Lasalle, 1971), where the input is
the cost matrix D, and output are the indices (row, col)
of assigned track-measurement pairs.
Algorithm 1: Track management with GNN.
1: if nMeasurements = 0 then
2: for i = 0 to nTargets do
3: DecreaseCounter(target[i]);
4: if Counter(target[i]) > 0 then
5: MaintainTarget(target[i]);
6: else
7: TerminateTarget(target[i]);
8: end if
9: end for
10: else
11: if nTargets = 0 then
12: for j = 0 to nMeasurements do
13: newTarget = CreateTarget(meas[ j]);
14: ResetCounter(newTarget);
15: end for
16: else
17: for i = 0 to nTargets do
18: for j = 0 to nMeasurements do
19: D(i, j) = Distance(target[i], meas[ j]);
20: if D(i, j) > ValidGate then
21: D(i, j) = ∞;
22: end if
23: end for
24: end for
25: (i ↔ j) = GNN(D);
26: for i = 0 to nAssocTargets do
27: if D(i, j(i)) ≤ ValidGate then
28: MoveTarget(target[i], meas[ j]);
29: IncreaseCounter(target[i]);
30: if Counter(target[i]) > MaxC then
31: Counter(target[i]) = MaxC;
32: end if
33: else
34: DecreaseCounter(target[i]);
35: if Counter(target[i]) = 0 then
36: TerminateTarget(target[i]);
37: end if
38: end if
39: end for
40: for j = 0 to nUnassocMeas do
41: newTarget = CreateTarget(meas[ j]);
42: ResetCounter(newTarget);
43: end for
44: end if
45: end if
6 EXPERIMENTAL RESULTS
We evaluated the proposed algorithms through pre-
recorded video sequences, with multiple people enter-
ing and leaving the scene, as well as interacting with
each other. The sequences have been simultaneously
recorded from four cameras, as described in Section
3, with a resolution of (752 × 480), and a frame rate
of 25 fps.
Before carrying out detection and tracking, state
grids are set up at all levels, respectively 10 × 10,
20 × 20 and 40 × 40 from the coarsest to the finest,
resulting in a total of 2100 grid cells, and the same
amount of silhouette templates are sampled off-line.
Since the area of interest is (6m × 4.2m), the corre-
sponding grid on the finest level has a resolution of
(150mm × 105mm).
Our current implementation of the oriented dis-
tance transform uses 12 discrete orientations, rang-
ing from 0 to π. As it computes each orientation
separately, they overall require about 0.25 sec/frame
for four images, whereas a single, standard distance
transform is computed in 0.1 sec/frame. Therefore,
the speed of our oriented distance transform is ac-
ceptable and reasonable in comparison with standard
distance transform. And the subsequent matching is
done very quickly for each hypothesis.
Figure 9 shows qualitative tracking results in a
multi-camera environment, with a complex back-
ground. In particular, the top row shows foreground
edges after edge-based background subtraction. Here
30 frames have been used for background learning,
where the threshold θ mentioned in Eq. (2) is set to
0.9. The middle row shows likelihood values onto
the finest grid, and the bottom row shows the corre-
sponding tracking results after data association, with
the projected cylinder silhouettes.
During data association, we keep a confirmation
time of 10 frames (which is the maximum value for
the consecutive detections counter) for keeping or re-
moving tracks. As can be seen from the results, there
are situations with significant occlusion from one or
more views. For instance, at frame 345, each two tar-
gets are occluded from some views, however, since
for the same pairs there are no occlusions from an-
other camera view, all targets are successfully de-
tected, thanks to the robustness of multi-camera fu-
sion and oriented DT matching. The system also
successfully handles targets entering and leaving the
scene.
In order to better evaluate the performance of our
system, we manually label the ground truth data for
our sequences, and compare the results of our tracker,
both in terms of position accuracy and robustness of
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
480

(a) Frame 185
(b) Frame 345
Figure 9: Performance of 3D people tracking. Shown are edge-based background subtraction, likelihood grids, and the
corresponding tracking results, on four camera views.
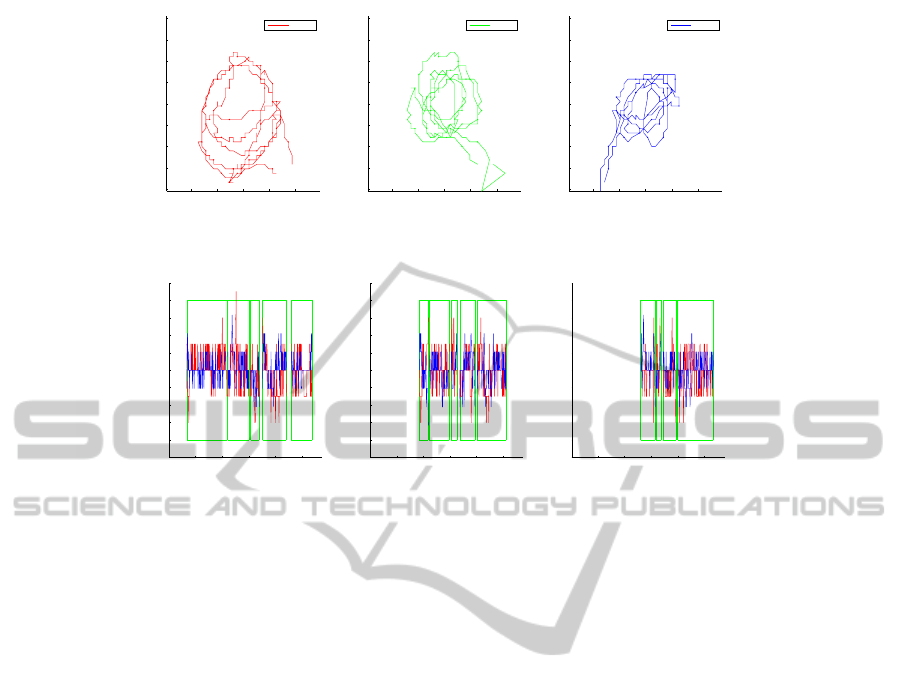
detection. Ground truth trajectories, labeled on the
finest grid, are depicted in Figure 10, where we can
see the challenges due to targets that keep close most
of the time, with mutual interactions and position ex-
changes.
Figure 11 shows the (X,Y ) position errors of our
tracking system. Because of the above mentioned
occlusions and dynamics, for each target the system
temporarily loses track, and recovers it again shortly
afterwards. That happens about 4-5 times per target
over the 550 frames of sequence, leading to several
sub-tracks with different IDs, as shown in Figure 11
by the green boxes.
Overall these results indicate that, despite the clut-
tered situation, position errors are considerably low
for all people, being most of the time under 100-
150mm, that corresponds to one cell of the high-
resolution grid. This is because of the local edge-
based matching which, despite the simplicity of the
model, is more precise with respect to global statis-
tics such as color histograms (Stillman et al., 1998),
or histograms of oriented gradients (Dalal and Triggs,
2005).
The execution time of the whole tracking proce-
dure is currently 2 FPS, on a desktop PC with In-
tel Core 2 Duo CPU (1.86 GHz), 1GB RAM and an
Nvidia GeForce 8600 GT graphic card.
7 CONCLUSIONS
In this paper, we presented a novel system for multi-
MULTI-CAMERA PEOPLE TRACKING WITH HIERARCHICAL LIKELIHOOD GRIDS
481
−2000 −1000 0 1000 2000
−2000
−1500
−1000
−500
0
500
1000
1500
2000
Target1
−2000 −1000 0 1000 2000
−2000
−1500
−1000
−500
0
500
1000
1500
2000
Target2
−2000 −1000 0 1000 2000
−2000
−1500
−1000
−500
0
500
1000
1500
2000
Target3
Figure 10: Ground-truth trajectories, sampled on the discretized grid (high-resolution).
100 200 300 400 500
−500
−400
−300
−200
−100
0
100
200
300
400
500
Frame
Position error on X/Y translation[mm]
100 200 300 400 500
−500
−400
−300
−200
−100
0
100
200
300
400
500
Frame
Position error on X/Y translation[mm]
100 200 300 400 500
−500
−400
−300
−200
−100
0
100
200
300
400
500
Frame
Position error on X/Y translation[mm]
Figure 11: Position error on X(red) and Y(blue) in world coordinates. From left to right are shown target 1, 2 and 3. The
green boxes correspond to sub-tracks estimated by our system.
ple people tracking in a multi-camera environment,
using a grid-based tracking by detection methodol-
ogy. A template hierarchy is constructed off-line, by
partitioning the state space. And frame-by-frame de-
tection is performed by means of hierarchical like-
lihood grids and clustered on the finest level, fol-
lowed by data association through the GNN approach.
Moreover, edge-based background subtraction has
been proposed for foreground segmentation, which
is quite robust to illumination changes, together with
an oriented distance transform, matching the silhou-
ette templates by taking gradient orientations into ac-
count, thus significantly reducing the rate of false
alarms. Our system initiates, maintains and termi-
nates tracks in a fully automatic way. Experimental
results over the video sequences also show that our
proposed system deals fairly well with mutual occlu-
sions.
As a future work, this system can be easily ex-
tended to include additional features, such as color or
motion, also can be scaled to more camera views, as
well as being used for tracking different objects, for
example 3D indoor tracking of flying quadrotors. In
addition, the individual components can still be fur-
ther optimized, both with respect to speed and per-
formance, graphics hardware is possibly need to be
exploited. Moreover, we plan to address the issue
of heavy occlusions between people, taking place for
longer periods. Re-identification after occlusions are
going to be done by using more specific features, such
as color or texture.
Besides these straightforward improvements, we
also plan to test and extend our system to more chal-
lenging scenarios, such as outdoor tracking with mul-
tiple models (such as people and cars), as well as peo-
ple tracking on mobile robots, with a non-static back-
ground and viewpoint.
REFERENCES
Andriluka, M., Roth, S., and Schiele, B. (2008).
People-tracking-by-detection and people-detection-
by-tracking. In IEEE Conference on Computer Vision
and Pattern Recognition.
Andriluka, M., Roth, S., and Schiele, B. (2010). Monocular
3d pose estimation and tracking by detection. In IEEE
conference on Computer Vision and Pattern Recogni-
tion(CVPR).
Bar-Shalom, Y. and Fortmann, T. E. (1988). Tracking and
data association. Academic Press, San Diego.
Bar-Shalom, Y. and Li, X. (1995). Multitarget-Multisensor
Tracking: Principles and Techniques. YBS Publish-
ing.
Borgefors, G. (1988). Hierarchical chamfer match-
ing: A parametric edge matching algorithm. IEEE
Trans. Pattern Analysis and Machine Intelligence,
10(6):849–865.
Burgeois, F. and Lasalle, J. C. (1971). An extension of
the munkres algorithm for the assignment problem to
rectangular matrices. Communications of the ACM,
14:802–806.
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
482

Cox, I. J. and Hingorani, S. L. (1996). An efficient im-
plementation of reid’s multiple hypothesis tracking al-
gorithm and its evaluation for the purpose of visual
tracking. IEEE Trans. Pattern Anal. Mach. Intell.,
18(2):138–150.
Dalal, N. and Triggs, B. (2005). Histograms of oriented
gradients for human detection. In Proceedings of the
2005 IEEE Computer Society Conference on Com-
puter Vision and Pattern Recognition, volume 1, pages
886–893, Washington, DC, USA. IEEE Computer So-
ciety.
Eng, H., Wang, J., Kam, A., and Yau, W. (2004). A bayesian
framework for robust human detection and occlusion
handling using a human shape model. In International
Conference on Pattern Recognition, volume 2, pages
257–260.
Fieguth, P. and Terzopoulos, D. (1997). Color-based track-
ing of heads and other mobile objects at video frame
rates. In Proceedings IEEE Conf. on Computer Vi-
sion and Pattern Recognition, pages 21–27, San Juan,
Puerto Rico.
Fortmann, T. E., Bar-Shalom, Y., and Scheffe, M. (1983).
Sonar tracking of multiple targets using joint prob-
abilistic data association. IEEE Journal of Oceanic
Engineering, 8(3):173–184.
Gavrila, D. M. (2000). Pedestrian detection from a moving
vehicle. In Proc. of European Conference on Com-
puter Vision, pages 37–49, Dublin, Ireland.
Gavrila, D. M. and Davis, L. S. (1996). 3-d model-based
tracking of humans in action: a multi-view approach.
In Proc. IEEE Computer Vision and Pattern Recogni-
tion, pages 73–80, San Francisco.
Isard, M. and Blake, A. (1996). Contour tracking by
stochastic propagation of conditional density. In Pro-
ceedings of the European Conference on Computer Vi-
sion, pages 343–356, Cambridge, UK.
Khan, S., Javed, O., Rasheed, Z., and Shah, M. (2001). Hu-
man tracking in multiple cameras. In Proceedings of
the 8th IEEE International Conference on Computer
Vision, pages 331–336, Vancouver, Canada.
Konstantinova, P., Udvarev, A., and Semerdjiev, T. (2003).
A study of a target tracking algorithm using global
nearest neighbor approach. In Proceeding of Inter-
national Conference on Computer Systems and Tech-
nologies.
Leibe, B., Schindler, K., and Gool, L. V. (2007). Coupled
detection and trajectory estimation for multi-object
tracking. In International Conference on Computer
Vision.
Li, L., Huang, W., Gu, I. Y. H., and Tian, Q. (2003). Fore-
ground object detection from videos containing com-
plex background. In Proceedings of the 11th ACM
International Conference on Multimedia, pages 2–10.
Nguyen, H. T., Worring, M., van den Boomgaard, R., and
Smeulders, A. W. M. (2002). Tracking nonparame-
terized object contours in video. IEEE Trans. Image
Process, 11(9):1081–1091.
Okuma, K., Taleghani, A., Freitas, N. D., Little, J., and
Lowe, D. (2004). A boosted particle filter: Multitar-
get detection and tracking. In European Conference
on Computer Vision.
Olsen, C. F. and Huttenlocher, D. P. (1997). Automatic
target recognition by matching oriented edge pixels.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 6:103–113.
Panin, G. (2011). Model-based visual tracking: the OpenTL
framework. Wiley-Blackwell. (to appear).
Panin, G., Lenz, C., Nair, S., Roth, E., Wojtczyk, M.,
Friedlhuber, T., and Knoll, A. (2008). A unifying
software architecture for model-based visual tracking.
In IS&T/SPIE 20th Annual Symposium of Electronic
Imaging, San Jose, CA.
Reid, D. B. (1979). An algorithm for tracking multi-
ple targets. IEEE Transaction on Automatic Control,
24(6):843–854.
Roh, M. C., Kim, T. Y., Park, J., and Lee, S. W. (2007).
Accurate object contour tracking based on boundary
edge selection. Pattern Recognition, 40(3):931–943.
Stauffer, C. and Grimson, W. E. L. (2000). Learning pat-
terns of activity using real-time tracking. IEEE Trans-
action on Pattern Analysis and Machine Intelligence,
22(8):747–757.
Stenger, B., Thayananthan, A., Torr, P. H. S., and Cipolla,
R. (2006). Model-based hand tracking using a hierar-
chical bayesian filter. IEEE Transactions on Pattern
Analysis and Machine Intelligence, 28:1372–1384.
Stillman, S., Tanawongsuwan, R., and Essa, I. (1998). A
system for tracking and recognizing multiple people
with multiple cameras. In In Proceedings of Second
International Conference on Audio-Visionbased Per-
son Authentication, pages 96–101.
Wren, C., Azarbayejani, A., Darrel, T., and Pentland, A.
(1997). Pfinder, real time tracking of the human body.
IEEE Transaction on Pattern Analysis and Machine
Intelligence, 19(7):780–785.
Wu, B. and Nevatia, R. (2007). Detection and tracking of
multiple, partially occluded humans by bayesian com-
bination of edgelet based part detectors. International
Journal of Computer Vision, 75(2):247–266.
MULTI-CAMERA PEOPLE TRACKING WITH HIERARCHICAL LIKELIHOOD GRIDS
483
