AFFINE SPHARM REGISTRATION

Neural Estimation of Afﬁne Transformation in Spherical Domain

Valentina Pedoia, Ignazio Gallo and Elisabetta Binaghi

Dipartimento di Informatica e Comunicazione, Universit`a dell’Insubria, Varese, Italy

Keywords:

3D Surface registration, SPHARM registration, Afﬁne transformation, RBF neural nework.

Abstract:

In this work we propose an algorithm to perform the afﬁne 3D surface registration using the shape model-

ing based on SPHerical HARMonic: called SPHARM. In the existing SPHARM registration algorithms the

alignment is obtained using the rotation properties, that allows to perform the 3D surface rotation transforming

only the spherical coefﬁcients. The major limit is that this approach aligns the surface only by rotation. We

propose a method to generalize this solution without lose the advantage to perform whole the registration pro-

cess in the spherical domain. An estimation of the coefﬁcients transformation that guarantees an afﬁnity in the

spatial domain is obtained by regression, using a set of RBF networks. The description of the 3D surface with

the spherical harmonic coefﬁcients is brief but comprehensive and provides directly a metric of the shape sim-

ilarity. Therefore, the registration is obtained aligning the SPHARM model thought the minimization of the

root mean square distance between the coefﬁcients vectors. Many experiments are performed to test the afﬁne

SPHARM registration algorithm which appears efﬁcient and effective compared with a standard registration

algorithm in the spatial domain.

1 INTRODUCTION

The 3D surface registration is dealt with extensively

in machine vision and computer graphics literature.

In the last few years a lot of techniques were pro-

posed (Xiao et al., 2005). Particular attention was

given on a parametric surface modeling. The most

widely used technique employs a description of a

radial or stellar surfaces v(θ, ϕ) with the spherical

harmonic decomposition (Ballard and Brown, 1982).

An extension of this work allows to describe more

general 3D simply connected surface using three

radial functions v(θ, ϕ) = x(θ, ϕ), y(θ, ϕ), z(θ, ϕ))

called SPHARM (SPHerical HARMonic modeling):

(Brechb¨uhler et al., 1995).

One of the most important ﬁeld of application of

SPHARM is medical imaging, where a good regis-

tration allows to compare shapes from the patients

acquired in different moments, or different patients,

or a comparison with standard atlas. In this spe-

ciﬁc ﬁeld an accurate and fast registration algorithm

is required. In most cases little transformations can

align two different anatomical surfaces, therefore ap-

proaches that solve efﬁciently and effectively the reg-

istration problem in this speciﬁc domain sacriﬁcing

the generality are still well-regarded. The spheri-

cal harmonic domain lends itself well to perform the

3D surface registration. The reasons are the follow-

ing: the SPHARM allows a brief representation of

the 3D shapes and directly provides a shape descrip-

tor. Moreover, the correlation of the harmonic coef-

ﬁcient’s degree and the level of detail of the descrip-

tion allows a hierarchical approach to the solution. Li

Shen (Shen et al., 2007) proposed a spherical surface

registration algorithm based on the minimization of

the root mean squared distance (RMSD) between two

SPHARM models. The major disadvantage is that

this approach solves the alignment problem only by

rotation, that is sufﬁcient for shape analysis but not

enough for registration.

In this paper we present a novel method based on

neural networks for registration SPHARM model by

afﬁne transformations. To obtain an analytical form

of the “afﬁne transformation” of the coefﬁcients is

an hard task. Indeed the orthogonality of the bases

is no longer guaranteed, hence the transformation of

each coefﬁcient is function of all the other. Pro-

ceeding from these considerations a numerical ap-

proach based on neural network was chosen. The

registration is obtained through the minimization of

the root mean squared distance (RMSD) between two

SPHARM models by the Broyden-Fletcher-Goldfarb-

Shanno (BFGS) algorithm (Head and Zerner, 1985).

The whole registration process is developed in the

197

Pedoia V., Gallo I. and Binaghi E..

AFFINE SPHARM REGISTRATION - Neural Estimation of Afﬁne Transformation in Spherical Domain.

DOI: 10.5220/0003318301970200

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2011), pages 197-200

ISBN: 978-989-8425-47-8

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

spherical domain ensuring the algorithm efﬁciency.

The experimental results show a good regression ca-

pability of the network and a good level of gen-

eralization. The dimensionality reduction obtained

through the SPHARM modeling and the goodness of

the shape descriptor allow an efﬁcient and effective

afﬁne registration algorithm. The standard SPHARM

alignment algorithm and our extension of this work

to perform afﬁne registration are described in the fol-

lowing.

2 SPHARM REGISTRATION

The aim of the SPHARM registration technique is the

use of the spherical parametrization of a 3D closed

surface for the description of the moving shape and

static template. Consider a 3D radial object repre-

sented by a set of vertices in the cartesian space v =

(x, y, z). The mapping of these vertices in the spherical

domain v(θ, ϕ) = ρ where θ ∈ [0, π] and ϕ ∈ [0, 2π] is

performed with surface parametrization (Floater and

Hormann, 2005). The spherical homogeneous sam-

pling of the space is obtained starting with an icosa-

hedron and iteratively subdividing each triangle into

four smaller triangles. A spherical surface can be de-

composed in a set of orthogonal bases through an in-

tegral transformation. The synthesis functions is the

following:

v(θ, ϕ) =

∑

l=0

∑

m=−l

(θ, ϕ) (1)

SPHARM surface modeling of a radial object bene-

ﬁts of the rotation property. The rotation of a sur-

face, deﬁned trough the three Euler angles (α, β, γ)

can be compute directly in the spherical domain. If

the spherical function represents a radial object, the

coefﬁcients rotation rotates, the parametrization and

also the object. The possibility to rotate a surface

only by rotating the harmonic expansion coefﬁcients

makes the SPHARM alignment algorithms very efﬁ-

cient but restricted only to the rigid transformations.

The spherical description of a surface is intrinsically

a metric of the shapes similarity. The surfaces align-

ment is obtained by aligning the SPHARM models

minimizing the root mean squared distance (RMSD)

between the harmonic coefﬁcients.

RMSD =

4π

max

∑

l=0

∑

m=−l

||c

1,l

− c

2,l

(2)

3 AFFINE SPHARM

REGISTRATION

In this section our novel method is presented, aimed

to generalize the SPHARM registration algorithm for

afﬁne transformations. To exploit the good features of

SPHARM modeling is necessary to perform the reg-

istration in the spherical domain. To this purpose, a

transformation of the spherical coefﬁcients that guar-

antees an afﬁne transformation in a space domain is

necessary. Instead of ﬁnding an analytical solution,

we attempt to solve the problem trough a Radial Ba-

sis Function (RBF) Neural Network. The afﬁnity is

a class of linear transformations that maps variables

in new variables, it consists of a linear transformation

followed by a translation.

′

= Ax+t (3)

To ﬁnd the afﬁne transformation in the SPHARM

domain we start by considering, at ﬁrst, only the

rotation: as shown by Li Shan, all the coefﬁcients

(α, β, γ) of the rotated surface are a linear combi-

nation of all the coefﬁcients of the same order and

lower degree.

(α, β, γ) =

∑

n=−l

(α, β, γ)c

(4)

Observing that the afﬁnity is a linear transformation

but don’t preserve the orthogonality of the basis we

can suppose that all the coefﬁcients c

(a) of the sur-

face after afﬁne transformation are a linear combina-

tion of all the other coefﬁcients.

(a) =

′

∑

k=0

∑

n=−k

(a)c

(5)

The analytical deﬁnition of the function T

(a) is a

critical aspect and is not guaranteed a closed-form

expression. To asses this problem the RBF net-

works were introduced to regress this function. One

of the easiest and effective way to model regression

is that of using a ﬁnite dimensional space of func-

tion spanned by a given basis. The RBF neural net-

work solves the regression problem by this way with

a very simple structure and, differently from other

types of neural network, like Multy Layer Percep-

tron (MLP), with a faster training (Buhmann and Buh-

mann, 2003). Moreover, the RBF works well if is

trained with many examples, as will be shown be-

low, in this speciﬁc application, the ground truth set

can be arbitrarily large. For each c

(a) one RBF

network is involved. As mentioned above the gen-

eration of the training set is easy: let be v

′

(θ, ϕ) the

surface v(θ, ϕ) after the afﬁne transformation A(a)

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

198

we can extract the c

of the original surface and the

(a) of the transformed surface. The input pat-

tern of the RBF network approximates the c

(a) is

, ...a

, c

−

, c

....c

, c

]. The training set is

composed of a series of afﬁne transformations of the

same object, the network can generalize only in the

domain of the training shape and the afﬁne transfor-

mations of this. Depending to the training set the net-

work can be specialized to a particular afﬁne deforma-

tions (scaling shearing,reﬂection...). The alignment

process is performed, like in the SPHARM registra-

tion by Li Shen , minimizing the root mean squared

distance (RMSD) between the harmonic coefﬁcients

(Eq. 2).

4 EXPERIMENT RESULTS

Several experiments, to asses the capability of the pro-

posed method and to ﬁnd the best network tuning are

performed. Once we have established the best net-

work conﬁguration in terms of number of radial basis

function and training cardinality, the performance are

evaluated for the two steps:

• the performance of the neural estimation of afﬁne

transformation of coefﬁcients: that involve the

network capability to regress the function and

generalize.

• the performance of afﬁne SPHARM registration:

that include the goodness of the SPHARM shape

descriptor and the capability of the minimization

algorithm to ﬁnd the afﬁne transformation that

best aligns the 3D surfaces. Our algorithm is

compared with a classical registration algorithm:

Demon registration (Kroon and Slump, 2009) in

terms of RMSE and execution time.

The networks are trained on 750 examples of afﬁne

transformation with scaling (s

, s

) from 0.8 to 1.2,

shearing (s

hxy

, s

hxz

, s

hyx

, s

hyz

, s

hzx

, s

hzy

) from -0.2 to 0.2

and rotation angles (α, β, γ) from −

. The

RMSE is computed between the surface transformed

in space domain trough the application of the afﬁne

matrix and performing a bicubic interpolation and

the surface obtained transforming the spherical coefﬁ-

cients with the network and reconstruction the surface

with the synthesis equation (Eq. 1). The networks

performance are tested, with the K-fold technique (10

experiments). In Figure 1 the results of one of the K-

fold experiment is shown for the training and test set,

the mean of RMSE is 0.95 for the ﬁrst and 1.16 for

the second. As expected the performances are better

for the training set but not so considerably, that is a

symptom of a good generalization.

50 100 150 200 250

Experiments

RMSE (mm)

RBF Affine transformation of Spherical Coefficients − Test Set

Transformation Error

Mean = 1.1623

100 200 300 400 500 600 700

Experiments

RMSE (mm)

RBF Affine transformation of Spherical Coefficients − Training Set

Transformation Error

Mean = 0.95315

Figure 1: Neural estimation of afﬁne coefﬁcients transfor-

mation performance on training set and test set.

The performance of the Afﬁne SPHARM regis-

tration are evaluated through the comparison with

a standard registration algorithm the ”MRI Modal-

ity transformation in Demon Registration” proposed

by Kroon and Slump. The algorithm is based on

a Thirlon Demon Registration (Thirion, 1998). The

experiments are performed with different types of

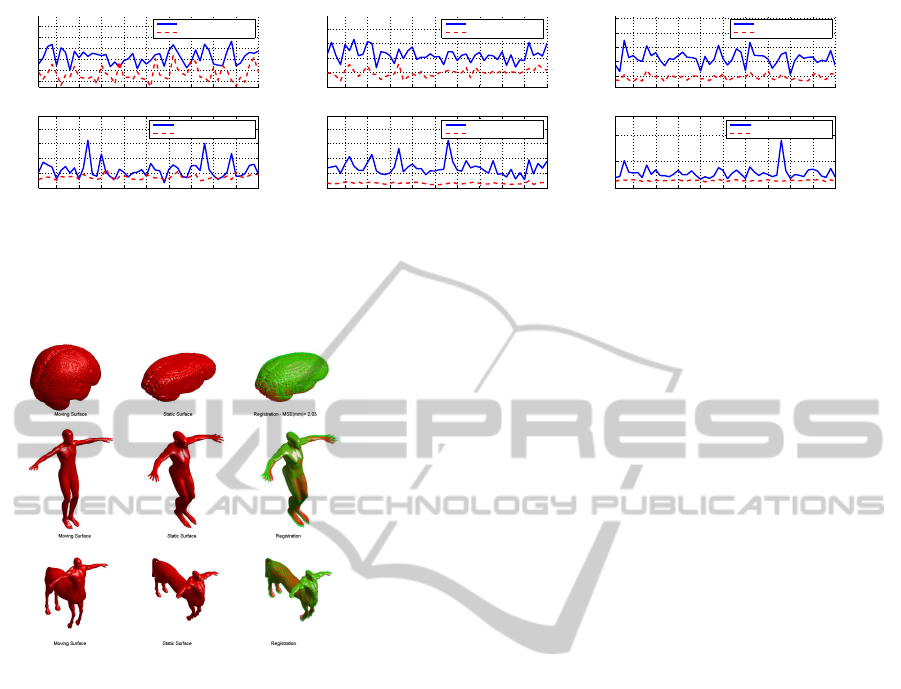
afﬁne transformations: scaling and rotation Figure

2(a), scaling and shearing 2(b), and a general afﬁne

transformation 2(c). The performance are evaluated

in term of RMSE and execution time. Note, the data

used are randomly chosen in the test set.

Observing the mean of the registration error the

good performance of the afﬁne SPHARM registration

is clear. The RMSE means in these experiments are

always lower for our algorithm rather the demon reg-

istration. Moreover, differently to the Demon Regis-

tration the afﬁne SPHARM performances appear in-

variant to the type of transformation.

In Figure 3 examples of surfaces alignment per-

formed by the afﬁne SPHARM registration are

shown. In the three cases the RBF networks are

trained with examples of the speciﬁc shape and afﬁne

transformations of these. These examples show how

the performance are good also with more complex

shape. Both the second and third examples belong

to TOSCA data set (Toolbox for Surface Comparison

and Analysis) (A. M. Bronstein, 2008):”david” and

”centaur”.

5 CONCLUSIONS

In this paper we propose an innovative method

to solve the 3D surface registration based on the

SHARM modeling. The results show good perfor-

mance of the neural approach for the estimation of the

coefﬁcients transformation. The chosen RBF network

allows a fast and easy training phase. Moreover the

possibility of creating an arbitrary large training set

AFFINE SPHARM REGISTRATION - Neural Estimation of Affine Transformation in Spherical Domain

199

5 10 15 20 25 30 35 40 45 50

Experiment

RMSE (mm)

Brain Data Set − Scaling And Rotation Affine Transform

Demon, Mean: 6.4338

SPHARM, Mean: 3.3772

5 10 15 20 25 30 35 40 45 50

Experiments

Matlab Time (s)

Demon, Mean: 24.3298

SPHARM, Mean: 14.5796

5 10 15 20 25 30 35 40 45 50

Experiments

RMSE (mm)

Brain Data Set − Scaling And Shearing Affine Transform

Demon, Mean: 11.121

SPHARM, Mean: 4.9678

5 10 15 20 25 30 35 40 45 50

Experiments

Matlab Time (s)

Demon, Mean: 27.4018

SPHARM, Mean: 6.3784

(a)

5 10 15 20 25 30 35 40 45 50

Experiments

RMSE (mm)

Brain Data Set − General Affine Transform

Demon, Mean: 11.1269

SPHARM, Mean: 4.3949

5 10 15 20 25 30 35 40 45 50

100

Experiments

Matlab Time (s)

Demon, Mean: 28.4175

SPHARM, Mean: 14.0552

(b)

Figure 2: Performance comparison between Afﬁne SPHARM Registration and Demon Registration in terms of registration

error end execution time for different afﬁnity class: (a) Scaling and Rotation (6 D.O.F.), Scaling and Shearing (9 D.O.F.),

General Afﬁnity (12 D.O.F.).

Figure 3: Examples of Surface registration: in the ﬁrst col-

umn the moving surfaces, in the second the static surfaces

and in the third the superposition of the static surfaces (red)

and the registered surfaces (green) are shown.

or specializing it to a particular set of transformation,

makes our approach very attractive. The experimen-

tal results shown good performance of the algorithm

in terms of execution time and registration error for

little deformation while the afﬁne SPHARM perfor-

mances worse in cases of big deformation. This prob-

lem is imputable to the loss of the basis orthogonality

thought the afﬁnity transform. In our future works we

want to establish a theoretical limit to application of

the afﬁne SPHARM, and a method to solve this limi-

tation.

REFERENCES

A. M. Bronstein, M. M. Bronstein, R. K. (2008). Numerical

geometry of non-rigid shapes. Springer.

Ballard, D. H. and Brown, C. M. (1982). Computer Vision.

Prentice-Hall, Englewood Cliffs, N.J.

Brechb¨uhler, C., Gerig, G., and K¨ubler, O. (1995).

Parametrization of closed surfaces for 3-d shape de-

scription. Comput. Vis. Image Underst., 61(2):154–

170.

Buhmann, M. D. and Buhmann, M. D. (2003). Radial Basis

Functions. Cambridge University Press, New York,

NY, USA.

Floater, M. S. and Hormann, K. (2005). Surface parameter-

ization: a tutorial and survey.

Head, J. D. and Zerner, M. C. (1985). A broyden–ﬂetcher–

goldfarb–shanno optimization procedure for molecu-

lar geometries. Chemical Physics Letters, 122(3):264

– 270.

Kroon, D.-J. and Slump, C. H. (2009). Mri modalitiy trans-

formation in demon registration. In ISBI’09: Proceed-

ings of the Sixth IEEE international conference on

Symposium on Biomedical Imaging, pages 963–966,

Piscataway, NJ, USA. IEEE Press.

Shen, L., Huang, H., Makedon, F., and Saykin, A. J. (2007).

Efﬁcient registration of 3d spharm surfaces. In CRV

’07: Proceedings of the Fourth Canadian Conference

on Computer and Robot Vision, pages 81–88, Wash-

ington, DC, USA. IEEE Computer Society.

Thirion, J. P. (1998). Image matching as a diffusion process:

an analogy with maxwell’s demons. Medical Image

Analysis, 2(3):243–260.

Xiao, G., Ong, S. H., and Foong, K. W. C. (2005). Efﬁ-

cient partial-surface registration for 3d objects. Com-

put. Vis. Image Underst., 98(2):271–294.

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

200