STEREO VISION HEAD VERGENCE USING GPU CEPSTRAL
FILTERING
Luis Almeida
Department of Informatics Engineering, Institute Polytechnic of Tomar, Tomar, Portugal
Paulo Menezes, Jorge Dias
Institute of Systems and Robotics, Department of Electrical and Computer Engineering
University of Coimbra, Coimbra, Portugal
Keywords:
Cepstrum, GPU, CUDA, Vergence.
Abstract:
Vergence ability is an important visual behavior observed on living creatures when they use vision to interact
with the environment. The notion of active observer is equally useful for robotic vision systems on tasks like
object tracking, fixation and 3D environment structure recovery. Humanoid robotics are a potential playground
for such behaviors. This paper describes the implementation of a real time binocular vergence behavior using
cepstral filtering to estimate stereo disparities. By implementing the cepstral filter on a graphics processing
unit (GPU) using Compute Unified Device Architecture (CUDA) we demonstrate that robust parallel algo-
rithms that used to require dedicated hardware are now available on common computers. The cepstral filtering
algorithm speed up is more than sixteen times than on a current CPU. The overall system is implemented
in the binocular vision system IMPEP (IMPEP Integrated Multimodal Perception Experimental Platform) to
illustrate the system performance experimentally.
1 INTRODUCTION
Vergence ability is an important visual behavior ob-
served on living creatures when they use vision to
interact with the environment. In binocular systems,
vergence is the process of adjusting the angle between
the eyes (or cameras) so that they are directed to-
wards the same world point. Robotic vision systems
that rely on such behavior have proven to simplify
tasks like object tracking, fixation, and 3D structure
recovery. Verging onto an object can be performed
by servoing directly from measurements made on the
image. The mechanism consists of a discrete con-
trol loop driven by an algorithm that estimates sin-
gle disparity from the two cameras. There are sev-
eral methods to measure stereo disparities (features
or area based correspondence, phase correlation based
method, etc) and although some of them present better
performance they were not used due to their computa-
tion requirements. Cepstral filtering is more immune
to noise than most other approaches ((Yeshurun and
Schwartz, 1989), (Coombs, 1992)), but computing the
Fast Fourier Transform (FFT) of images and inverse
FFT presents some real-time challenges for the pro-
Figure 1: Integrated Multimodal Perception Experimental
Platform (IMPEP) (POP, 2010) and NVIDIA GPU used for
data parallel processing on the vergence process.
cessing devices.
This work describes the implementation of a real-
time binocular vergence behavior using GPU cepstral
filtering to estimate stereo disparities. By implement-
ing the real-time cepstral filter on a current graphics
processing unit (GPU) using Compute Unified Device
Architecture (CUDA) (NVIDIA, 2010) we demon-
strate that robust parallel algorithms can be used on
common computers. The overall system is imple-
mented in the binocular vision system IMPEP (POP,
2010) (figure 1) to experimentally demonstrate the
system performance. The main body of the cepstral
665
Almeida L., Menezes P. and Dias J..
STEREO VISION HEAD VERGENCE USING GPU CEPSTRAL FILTERING.
DOI: 10.5220/0003319406650670
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2011), pages 665-670
ISBN: 978-989-8425-47-8
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

algorithm consists of a 2-D FFT, a point transform
(the log of the power spectrum), and the inverse 2-D
FFT. It takes 0.43 ms to process an [256x256] image.
By using the NVIDIA GPU multicore processors ar-
chitecture and parallel programming we speed up the
cepstral filtering algorithm more than sixteen times
than on a CPU version using an optimized FFT and
running on one core of a 2.4-GHz Core2 Quad Q6600
processor (Garland et al., 2008). Figure 2 presents
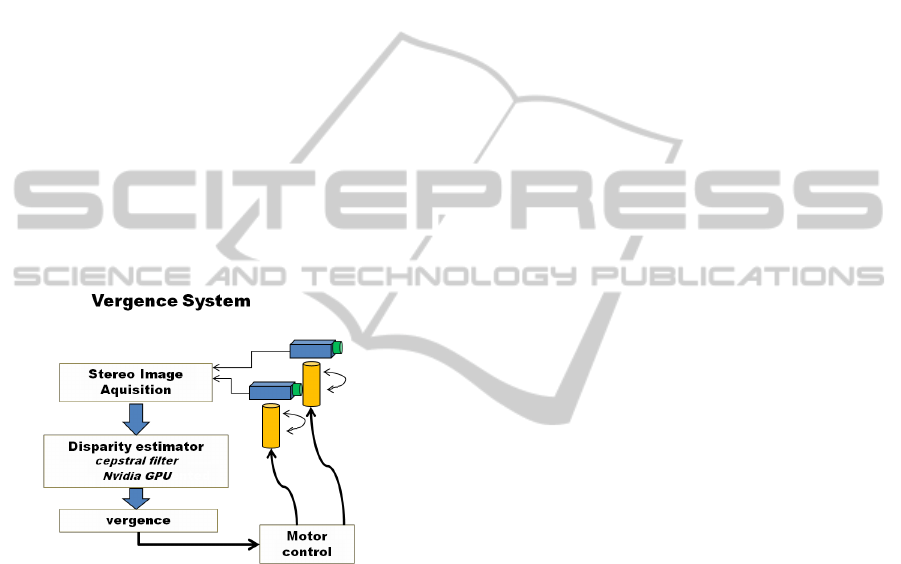
an schematic overview of the system. The goal of
the control strategy is to compensate the disparity be-
tween the cameras. The complete vergence control it-
erations cycle can be performed in 31ms (f=32.25Hz).
The use GPU Cepstral Filtering to perform vergence
on binocular head systems is, to our knowledge, an
new contribution for the state-of-art. Gaze holding
behaviors and vergence processes are very useful for
the emergent humanoid robotics area that aims to
mimic humans. The following text presents the back-
ground for disparity estimation using cepstral filter-
ing, a description of CUDA IMPEP implementation,
experimental results and conclusions.
Figure 2: IMPEP vergence system architecture overview.
2 BACKGROUND AND RELATED
WORK
Animals, especially predators, that have their eyes
placed frontally can use information derived from
the different projection of objects onto each retina
to judge depth. By using two images of the same
scene obtained from slightly different angles, it is pos-
sible to triangulate the distance to an object with a
high degree of accuracy. For primates like ourselves
the need for a vergence mechanism is obvious. Hu-
man eyes have non-uniform resolution, so we need
a way to direct both foveas at the same world point
so as to extract the greatest possible amount of infor-
mation about it. The human brain has an extraordi-
nary ability to extract depth information from stereo
pairs, but only if the disparities fall within a lim-
ited range. Verging on surfaces usually constrains
points near the fixation point to fall inside this range
(Coombs, 1992),(Almeida and Dias, 1999). Binoc-
ular systems heads have been developed in recent
decades. For example, VARMA head (Dias et al.,
1998), MDOF head (Batista et al., 1995), Rochester
robot (Brown, 1988) and the KTH robot head (Bet-
sis and Lavest, 1994) were capable of mimicking
human head motion. More recent robot heads in-
clude the POP head (Perdigoto et al., 2009) used on
the Bayesian Approach to Cognitive Systems project
(IMPEP)(Ferreira et al., 2010), the LIRA-head (Na-
tale et al., 2002), where acoustic and visual stimuli
are exploited to drive the head gaze; the Yorick head
(Eklundh and Bjrkman, 2005) and the Medusa head
where high-accuracy calibration, gaze control, control
of vergence or real-time speed tracking with log-polar
images were successfully demonstrated.
In binocular camera systems, the vergence pro-
cess has to adjust the angle between the cameras, by
controlling the cameras pan angle, so that both sen-
sors are directed at the same world point. The pro-
cess must estimate the angle between the current di-
rection of the non-dominant camera optical axis and
the direction from the camera center to the desired
direction (fixation point). The compensation angle
is driven by continuously minimizing the binocular
disparity. The IMPEP cameras do not have foveas.
Even so, there are good reasons to have a low-level
mechanism that maintains vergence. Verging the eyes
provides a unique fixation point invariant that may be
useful to higher level processes. It guarantees that the
depth of at least one world point is known, even if
we do not attempt stereo reconstruction in the usual
sense. Additionally, by acquiring images that contain
the focus of interest near the optical axis it is possible
to avoid the effects due the camera lens radial distor-
tion. There are many different possible models for im-
plementing vergence using disparity in the context of
a robotic binocular system ((Coombs, 1992),(Taylor
et al., 1994),(Dias et al., 1998),(Kwon et al., 2009),
(Perdigoto et al., 2009)). For example, by means
of saliency detection or using stereo-matching tech-
niques such as: phase correlation method like cep-
stral filtering, area based matching and feature-based
matching. Scharstein and Szeliski (Scharstein and
Szeliski, 2002), and Brown (Brown et al., 2003),
present thorough reviews of these techniques.
This work uses cepstral filtering to obtain a single
disparity due their immunity to noise ((Yeshurun
and Schwartz, 1989), (Coombs, 1992)) and proves
that the associated exponential calculus overhead
(FFT) can be overcome by common parallel GPU’s.
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
666

According to Yeshurun, size changes of up to 15
percent and rotations of ten degrees of one of the
stereo frames can be routinely accepted by this
algorithm. Considerable intensity changes can be
applied to one of the stereo frames without disrupting
the algorithm.
Disparity estimation by cepstral filtering.
A single disparity is estimated from the two cameras
using the cepstral filtering. The cepstrum of a signal is
the Fourier transform of the log of its power spectrum.
Cepstral filter it is a known method of measuring au-
ditory echo and it was introduced by Bogert (Bogert
et al., 1963). The power spectrum of an audio signal
with an echo present has a strong and easily identi-
fied component which is a direct measure of the echo
period.
The binocular disparity measurement is obtained
by applying of a non local filter (cepstral filter), fol-
lowed by peak detection. Yeshurun and Schwartz
((Yeshurun and Schwartz, 1989), (Coombs, 1992))
developed a method of using two-dimensional cep-
strum as a disparity estimator. The first step of their
method is to extract sample windows of size h x w
from left and right images. The sample windows are
then spliced together along one edge to produce an
image f (x, y) of size h x 2w. Assuming that right and
left images differ only by a shift, the spliced image
may be thought as the original image at (0, 0) plus
an echo at (w + d
h
, d
v
), where d
h
and d
v
are the hor-
izontal and vertical disparities. The periodic term in
the log power spectrum of such signal will have fun-
damental frequencies of w + d
h
horizontally and d
v
vertically. These are high frequencies relative to the
window size. The image dependent term, by con-
trast will be composed of much lower frequencies,
barring pathological images. Thus, as some authors
(Yeshurun and Schwartz, 1989) show, the cepstrum
of the signal will usually have clear, isolated peaks
at (
+
−
(w + d
h
),
+
−
d
v
). The image f(x,y) composed by
the left and right images pairs can be mathematically
represented as follow:
f (x, y) = s(x, y)∗ [δ(x, y) + δ(x − (W + d
h
), y − d
v
)]
(1)
where s(x, y) is the left image, δ(x, y) is the delta func-
tion, W the image width and ∗ operator represents two
dimensional convolution. The Fourier transform of
such image pair is
F(u, v) = S(u, v).(1 + e
− j2π[(W+d
h
)u+(d
v
)v]
) (2)
The power spectrum and the logarithm of equation
(1), are:
|F(u, v)|
2
= |S(u, v).(1 + e
− j2π[(W+d
h
)u+(d
v
)v]
)|
2
(3)
logF(u, v) = logS(u, v)+log(1+e
− j2π[(W+d
h
)u+(d
v
)v]
)
(4)
and the Cepstral filter is the inverse Fourier transform
of equation (4):
F
−1
[logF(u, v)] = F
−1
[logS(u, v)]
+
∞
∑
1
(−1)
n+1
δ(x − n(W + d
h
), y − nd
v
)
n
(5)
In the equation (5) , the second term represents
the prominent peak located in the output of Cepstral
filter response. By determining these peak points po-
sitions its possible to obtain disparity (example on fig-
ure 3). The dominant global disparity are related with
the major peaks locations (marked with blue dots) and
it is the cue for the disparity estimation.
Figure 3: Spliced images 2x[40x30] and the respective sur-
face plot of the power spectrum of the cepstral filter (on bot-
tom). Peaks are clearly visible at dominant global disparity
location (marked with blue dots).
3 VISUAL VERGENCE USING
GPU CEPSTRAL DISPARITY
FILTERING
3.1 Implementation on GPU using
CUDA
In CUDA terminology, the GPU is called the device
and the CPU is called the host (figure 4). A CUDA
device consists of a set of multicore processors. Each
multicore processor is simply referred to as a multi-
processor. Cores of a multiprocessor work in a SIMD
fashion.
STEREO VISION HEAD VERGENCE USING GPU CEPSTRAL FILTERING
667

Global Memory
Constant Memory
Device (grid)
Host
Texture Memory
Block(1,0)
Regs
Shared Memory
Regs
Thread
(0,0)
()
Thread
(1,0)
()
Block(0,0)
Regs
Shared Memory
Regs
Thread
(0,0)
()
Thread
(1,0)
()
LM LM LM LM
Figure 4: GPU Hardware Architecture.
Our system uses the GeForce 9800 GTX+ with 128
cores and 512MB of dedicated memory to process
the cepstral filter. The main body of the cepstral al-
gorithm consists of a 2-D FFT, a point transform (the
log of the power spectrum), and the inverse 2-D FFT.
The CUDA program is organized into a host program,
consisting of one sequential thread running on the
host CPU, and several parallel kernels executed on the
parallel processing device (GPU). A kernel executes a
scalar sequential program on a set of parallel threads.
For this 2D cepstrum algorithm we developed a
GPU custom kernel to perform the point-wise abso-
lute log in parallel using 16 blocks with 128 threads
per block, a GPU kernel to pad input data arrays with
zeros (FFT requirement), GPU FFT transformations
and all data allocation and data transfer procedures.
A summarized global system algorithm loop is pre-
sented on figure 5. The host computer performs the
stereo image acquisition 2x[640x480] and the prepro-
cessing step. It consists on the image down sampling
2x[53x40], the splicing of resulting images and the re-
arrangement of the data layout for complex data. Af-
ter that, the data is uploaded to the GPU, zero padding
input data operation is initialized and the CUDA data
arrays are bind to texture references to speed up the
memory access. Once the data on the GPU, a kernel
of threads performs in parallel the zero padding, the
FTT, the point-wise absolute log and the inverse FFT.
The results are sent back to the host where is per-
formed the peak detection and the disparity estima-
tion. By minimizing actively the disparity through the
cameras angle changes we perform the vergence con-
trol. The 2D GPU FFT routines are implemented us-
ing CUFFT the Fast Fourier Transform (FFT) library.
Memory access optimization are performed through
in place and out of place transforms feature for real
and complex data. A plan of execution for a partic-
ular FFT size and data type is created to completely
specify the optimal parameter configuration and once
Host CPU
Down Sampling
Spliced image
Peak detection & Disparity estimation
Vergence control (Carmen)
Down Sampling
Rearrange the data layout for complex data (FFT
requirement)
Uploading to GPU and padding input data
(Initializing data storage with zeroes)
Binding Cuda arrays to texture references
Reading back GPU results
Display Results
0,43 ms
31 ms
26 ms
Left Image Acquisition Right Image Acquisition
Device GPU (parallel multi thread)
Padding input data arrays
FFT -> abs_log -> iFFT
Figure 5: Schematic block diagram of GPU cepstral filter-
ing algorithm.
created, the system stores whatever state is needed to
execute the plan multiple times without recomposing
the configuration.
3.2 Experiments
Experiment 1 - Image Alignment.
Figure 6 presents the real-time image alignment pro-
cess frame sequence driven by the vergence control
algorithm when an object is ”instantly” positioned in
front of the system. Both cameras changes alternate
their angles to minimize the disparity. The left cam-
era angle values (red line) and right camera angle val-
ues (green line) in degrees during the image alignment
process are shown on figure 7. This experiment per-
forms only an image alignment, does not foveate. The
performance measurements, according the schematic
block diagram of figure 5, are shown on table 1. These
measurements take into account the firewire image
acquisition overhead and the Carmen messaging over-
head.
In order to measure the GPU and CPU perfor-
mances we stopped the real time image acquisition
and the Carmen messaging. It was used a preloaded
stereo image pair. As can be seen on table 2, the pure
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
668

Figure 6: Real-time image alignment process frame se-
quence (each colum pair is an stereo pair).
Figure 7: The left camera angle values (red line) and right
camera angle values (green) in degrees during the image
alignment process.
computation, the PCI-Express data transfer and dis-
play takes only 6.9 to 9.1 milliseconds. The GPU
computation (FFT, abs, log, iFFT) takes only 0.43 ms
on both measurements to process an 256x256 image
data. By migrating CPU tasks to the GPU it is possi-
ble to improve the algorithms.
Experiment 2 - Image Alignment with a Dominant
Camera.
We have also implemented an experience where the
left camera follows a color object (a ball) using CPU
OpenCV camshift algorithm (OpenCV, 2010) and the
right camera equally follows the object while trying
to minimize the disparity using the GPU Cepstral Fil-
tering (figure 8). By demonstrating this behavior we
show that binocular heavy tracking algorithms can be
Table 1: Processing time measurements A.
Task Set A Proc. Time
GPU (FFT abs log iFFT)
[256x256] 0.43ms
Image acquisition
2x[640x480 ] & preprocessing 26 ms
Complete iteration cycle 31 ms
with vergence control (f=32.25Hz)
Table 2: Processing time measurements B.
Task Set B Proc. Time
GPU (FFT abs log iFFT)
[256x256] 0.43ms
Image preloaded
2x[640x480] & preprocessing 3.2-4.5 ms
Complete iteration cycle 6.9-9.1 ms
without vergence control (f=144.92Hz
and image aquisition -109.89Hz)
Figure 8: Right camera follows left camera during a track-
ing task.
applied to one only camera allowing CPU extra com-
putational power for other tasks. Work on vergence
controller should be carry out to enable smooth move-
ments.
4 RESULTS AND CONCLUSIONS
The purpose of these experiments is to prove the ap-
plicability of parallel algorithms to robotic computer
vision common tasks using common hardware at af-
fordable costs and with speedup gains. The first ex-
periment depicts the use of a robust algorithm to per-
form vergence. The real-time characteristic, 31 ms
(f=32.25Hz) for the complete iteration cycle with ver-
gence control is only achieved through the parallel ap-
proach. Notice that, what use to be the heavy part of
STEREO VISION HEAD VERGENCE USING GPU CEPSTRAL FILTERING
669

the cepstral algorithm (i.e. the 2-D FFT, a point trans-
form (log of the power spectrum) and the inverse 2-D
FFT) takes now only 0.43 ms on the GPU. FFT rou-
tine is eight times faster than a CPU version using
an optimized FFT running on one core of a 2.4-GHz
Core2 Quad Q6600 processor (Garland et al., 2008).
As the cepstral algorithm performs two FTT opera-
tions and the absolute log operation in parallel, the
speedup is more than sixteen times faster than a CPU
version.
By implementing the cepstral filter on a graphics
processing unit (GPU) using Compute Unified Device
Architecture (CUDA) we demonstrate that robust par-
allel algorithms that use to require dedicated hardware
are now available on common computers for real time
tasks. Using the GPU for low level tasks allows CPU
extra computational power for other high level tasks.
The cepstral filtering algorithm speed up is more than
sixteen times than on a CPU and the use of GPU Cep-
stral Filtering to perform vergence on binocular head
systems is, to our knowledge, an contribution for the
state-of-art. Future work includes the identification of
algorithms tasks that could gain on GPU paralleliza-
tion.
REFERENCES
Almeida, L. and Dias, J. (1999). Dense depth maps using
stereo vision head. In SIRS99 the 7th International
Symposium on Intelligent Robotic Systems, Coimbra,
Portugal.
Batista, J., Dias, J., Ara
´
ujo, H., and de Almeida, A. T.
(1995). The isr multi-degree of freedom active vi-
sion robot head: Design and calibration. In SMART
Program Workshop, pages 27–28. Instituto Superior
Tecnico, Lisboa, Portugal.
Betsis, D. and Lavest, J. (1994). Kinematic calibration of
the kth head-eye system. In ISRN KTH.
Bogert, B., Healy, M., and Tukey, J. W. (1963). The
quefrency alanysis of time series for echoes: Cep-
strum, pseudo-autocovariance, cross-cepstrurn, and
saphe cracking. In Proc. Symp. Time Series Analysis,
pages 209–243. John Wiley and Sons.
Brown, C. M. (1988). The rochester robot. Tech. Report
257.
Brown, M. Z., Burschka, D., and Hager, G. D. (2003). Ad-
vances in computational stereo. IEEE Trans. Pattern
Anal. Mach. Intell., 25(8):993–1008.
Coombs, D. J. (1992). Real-time gaze holding in binocu-
lar robot vision. PhD thesis, University of Rochester.
Dept. of Computer Science.
Dias, J., Paredes, C., Fonseca, I., Ara
´
ujo, H., Batista, J., and
de Almeida, A. T. (1998). Simulating pursuit with
machines– experiments with robots and artificial vi-
sion. IEEE Transactions on Robotics and Automation,
14(1):1–18.
Eklundh, J. O. and Bjrkman, M. (2005). Recognition of
objects in the real world from a systems perspective.
Kuenstliche Intelligenz, 19(2):12–17.
Ferreira, J. F., Lobo, J., and Dias, J. (2010). Bayesian real-
time perception algorithms on gpu - real-time imple-
mentation of bayesian models for multimodal percep-
tion using cuda. Journal of Real-Time Image Process-
ing, Special Issue, ISSN: 1861-8219:87–106.
Garland, M., Grand, S. L., Nickolls, J., Anderson, J., Hard-
wick, J., Morton, S., Phillips, E., Zhang, Y., and
Volkov, V. (2008). Parallel computing experiences
with cuda. IEEE Micro, 28(4):13–27.
Kwon, K.-C., Lim, Y.-T., Kim, N., Song, Y.-J., and Choi,
Y.-S. (2009). Vergence control of binocular stereo-
scopic camera using disparity information. Journal of
the Optical Society of Korea, 13(3).
Natale, L., Metta, G., and Sandini, G. (2002). Development
of auditory-evoked reflexes: Visuo-acoustic cues inte-
gration in a binocular head. Robotics and Autonomous
Systems, 39(2):87–106.
NVIDIA (2010). NVIDIA CUDA C Programming Guide
3.1. NVIDIA Corp.
OpenCV (2010). OpenCV (Open Source Computer Vision),
http://opencv.willowgarage.com.
Perdigoto, L., Barreto, J. P., Caseiro, R., and Ara
´
ujo, H.
(2009). Active stereo tracking of multiple free-moving
targets. In CVPR, pages 1494–1501.
POP, P. (2010). Project POP (Perception on Purpose),
http://perception.inrialpes.fr/POP/.
Scharstein, D. and Szeliski, R. (2002). A taxonomy and
evaluation of dense two-frame stereo correspondence
algorithms. International Journal of Computer Vision,
47(1-3):7–42.
Taylor, J., Olson, T., and Martin, W. (1994). Accurate ver-
gence control in complex scenes. CVPR, 94:540–545.
Yeshurun, Y. and Schwartz, E. L. (1989). Cepstral filtering
on a columnar image architecture: A fast algorithm
for binocular stereo segmentation. IEEE Transactions
on Pattern Analysis and Machine Intelligence, PAMI-
11(7):759–767.
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
670