OUTDOOR ILLUMINATION ESTIMATION IN IMAGE SEQUENCES

FOR AUGMENTED REALITY

Claus B. Madsen and Brajesh B. Lal

Department of Architecture, Design & Media Technology, Aalborg University, Aalborg, Denmark

Keywords:

Illumination, Augmented Reality, Shadows, Stereo, HDR.

Abstract:

The paper presents a technique for estimating the radiance of the sky and sun for outdoor, daylight illumi-

nation conditions. Shadows cast by dynamic objects are detected using color imagery, combined with depth

information from a commercial stereo camera setup. Color information extracted from the detected shadows

is used to estimate the radiance of the sun. The technique does not require special purpose objects in the scene,

nor does it require High Dynamic Range imagery. Results are demonstrated by rendering augmented objects

into real images with shading and shadows which are consistent with the real scene.

1 INTRODUCTION

For photo-realistic Augmented Reality (AR) the goal

is to render virtual objects into real images to create

the visual illusion that the virtual objects are real. A

crucial element in achieving this illusion is to have

a sufﬁciently correct model of the illumination con-

ditions in the scene to be able to render the virtual

objects with scene consistent shading and to render

correct shadow interaction between real and virtual

geometry.

This paper presents an adaptive illumination es-

timation technique for outdoor daylight scenes. The

technique uses color image sequences, combined with

live stereo data, to estimate the radiance of a sky dome

(hemi-sphere) and the radiance of the sun. Both radi-

ances are estimated in three color channels. The po-

sition of the sun is computed procedurally from GPS

and date/time information. Together, this illumination

environment (sky dome and sun) can be used to render

virtual objects into the scene. As an additional beneﬁt

the stereo information provides 3D scene information

to cast shadows on and to handle occlusion between

real and virtual objects. Figure 1 shows an example

result.

The main contribution in this work lie in the fact

that the illumination is estimated directly from the im-

age sequence with no need for special purpose ob-

jects in the scene, and no need for acquiring omni-

directional High Dynamic Range environment maps

(light probes) prior to augmentation.

The paper is organized as follows. Section 2

Figure 1: Frame 139 of a 200 frame sequence. The diffuse

grey box and the three glossy spheres are rendered into the

scene with illumination estimated from the shadow cast by

the walking person.

describes related work, and section 3 describes the

assumptions behind the presented work. Section 4

presents the theoretical framework for our approach,

both in terms of detecting shadows and in terms of

estimating scene illumination from detected shadows.

Sections 5 and 6 present the dynamic shadow detec-

tion and the illumination estimation, respectively. Ex-

perimental results are presented in section 7, followed

by discussions and ideas for future research in section

8. Finally, section 9 presents concluding remarks.

129

B. Madsen C. and B. Lal B..

OUTDOOR ILLUMINATION ESTIMATION IN IMAGE SEQUENCES FOR AUGMENTED REALITY.

DOI: 10.5220/0003321301290139

In Proceedings of the International Conference on Computer Graphics Theory and Applications (GRAPP-2011), pages 129-139

ISBN: 978-989-8425-45-4

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

2 RELATED WORK

A survey of real scene illumination modelling for

Augmented Reality is given in (Jacobs and Loscos,

2004). The survey indicates that there is no one pre-

ferred or most popular family of approaches. No

technology has matured to the point of outperform-

ing other types of approaches. In fact, any approach

offers a set of possibilities at the price of a set of as-

sumptions or limitations, leaving the application sce-

nario to deﬁne which approach to choose.

There are three main categories of approaches:

1) omni-directional environment maps, 2) placing

known objects/probes in the scene, and 3) manually

or semi-manually model the entire scene, including

the light sources, and perform inverse rendering.

The most widely used approach is to capture the

scene illumination in a High Dynamic Range (HDR),

(Debevec and Malik, 1997), omni-directional envi-

ronment map, also called a light probe. The technique

was pioneered by Debevec in (Debevec, 1998) and

used in various forms by much research since then,

e.g., (Barsi et al., 2005; Debevec, 2002; Gibson et al.,

2003; Madsen and Laursen, 2007). The technique

gives excellent results if the dominant illumination in

the scene can be considered inﬁnitely distant relative

to the size of the augmented objects. The drawbacks

are that it is time-consuming and impractical to ac-

quire the environment map whenever something has

changed in the scene, for example the illumination.

Illumination adaptive techniques based on the envi-

ronment map idea have been demonstrated in (Havran

et al., 2005; Kanbara and Yokoya, 2004) but require a

prototype omni-directional HDR camera, or a reﬂec-

tive sphere placed in the scene, respectively.

The other popular family of approaches is based

on requiring the presence of a known object in the

scene. Sato et al. analyze the shadows cast by a

known object, (Sato et al., 1999a; Sato et al., 1999b)

onto a homogeneous Lambertian surface, or require

images of the scene with and without the shadow cast-

ing probe object. Hara et al., (Hara et al., 2005) ana-

lyze the shading of a geometrically known object with

homogeneous (uniform albedo) Lambertian object, or

require multiple images with different polarizations,

to estimate the illumination direction of a single point

light source. Multiple light sources can be estimated

from the shading of a known object with homoge-

neous Lambertian reﬂectance using the technique de-

scribed in (Wang and Samaras, 2008).

The last family of approaches do not estimate il-

lumination per se as they rely on modelling the en-

tire scene in full detail, including modelling the ge-

ometry and the radiances of the light sources. The

modelling process is labor intensive. Given the full

description of the scene and images of it (in HDR if

needed) inverse rendering can be performed to esti-

mate the parameters of applicable reﬂectance func-

tions of scene surfaces. Subsequently virtual objects

can be rendered into the scene with full global illumi-

nation since all required information is known. Exam-

ples include (Boivin and Gagalowicz, 2001; Boivin

and Gagalowicz, 2002; Loscos et al., 2000; Yu et al.,

1999).

A ﬁnal piece of related work does not fall into the

above categories, as it is the only representative of this

type of approach. Using manually identiﬁed essential

points (top and bottom point of two vertical structures

and their cast shadow in outdoor sunlight scenes) the

light source direction (the direction vector to the sun)

can be determined, (Cao et al., 2005).

In summary existing methods either require pre-

recorded full HDR environment maps, require homo-

geneous Lambertian objects to be present in the scene,

require total modelling of the scene including the il-

lumination, or require manual identiﬁcation of essen-

tial object and shadow points. None of the mentioned

techniques offer a practical solution to automatically

adapt to the drastically changing illumination condi-

tions of outdoor scenes.

The approach proposed in this paper addresses

all of these assumption and/or constraints: it does

not require HDR environment maps, nor HDR image

data, it does not require objects with homogeneous

reﬂectance (entire objects with uniform reﬂectance),

it does not require manual modelling of the illumina-

tion (in fact the illumination is estimated directly) and

there is no manual identiﬁcation of essential points.

3 ASSUMPTIONS BEHIND

APPROACH

Our approach rests on a few assumptions that are

listed here for easy overview. It is assumed that we

have registered color and depth data on a per pixel

level. High Dynamic Range color imagery is not re-

quired; standard 8 bit per color channel images sufﬁce

if all relevant surfaces in the scene are reasonably ex-

posed. In this paper the image data is acquired using

a commercially available stereo camera, namely the

Bumblebee XB3 from Point Grey, (PointGrey, 2009).

It is also assumed that the response curve of the color

camera is approximately linear. The Bumblebee XB3

camera is by no means a high quality color imaging

camera but has performed well enough. It is also as-

sumed that the scene is dominated by approximately

diffuse surfaces, such as asphalt, concrete, or brick,

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

130

see ﬁgure 1 for an example. There is no homogeneity

assumption, and in section 8 we will brieﬂy describe

ongoing/future work to relax the diffuse surface con-

straint.

To be able to procedurally compute the direction

vector to the sun we need to know the Earth location

in latitude/longitude (acquired from GPS), the date

and time of the image acquisition, and we assume that

the camera is calibrated (extrinsic parameters for po-

sition and orientation) to a scene coordinate system

with xy-plane parallel to a horizontal ground plane

(z-axis parallel to the direction of gravity), and x-axis

pointing North. The checkerboard in ﬁgure 1 is used

for camera calibration.

4 ILLUMINATION MODEL

The purpose of this section is to establish the theoret-

ical foundation for both the shadow detection and the

illumination estimation. All expressions in this pa-

per relating to pixel values, radiometric concepts, and

surface reﬂectance et cetera are color channel depen-

dent expressions and are to be evaluated separately for

each color channels.

If the response curve of the camera is linear the

pixel value in an image is proportional to the outgoing

radiance from the scene surface point imaged to that

pixel, (Dutr

e et al., 2003). The constant of proportion-

ality depends on things such as lens geometry, shutter

time, aperture, camera ISO setting, white balancing

settings, etc. If the unknown constant of proportion-

ality is termed c the value P of a pixel corresponding

to a point on a diffuse surface can be formulated as:

P = c · ρ · E

(1)

where ρ is the diffuse albedo of the surface point, and

is the incident irradiance on the point. ρ times E

yields the radiosity from the point, division by π gives

the radiance, and c is the camera constant mapping

radiance to pixel value. For a point in sunlight the in-

cident irradiance, E

, is the sum of irradiance received

from the sun and from the sky, provided that we can

disregard indirect Global Illumination from other sur-

faces in the scene, (for a discussion on this please re-

fer to section 8).

The irradiance received from the sun can be for-

mulated as:

sun

= ~n ·

s · E

⊥

(2)

where ~n is the unit surface normal at the point,

s is

the unit direction vector to the sun (both relative to

the scene coordinate system) and E

⊥

is the irradiance

produced by the sun on a point with a normal pointing

straight into the sun. The direction vector to the sun

is computed procedurally from the GPS and date/time

information using the approach described in (Blanco-

Muriel et al., 2001).

The irradiance from the sky can be formulated as:

sky

= V

· E

⊥

(3)

where V

is the fraction of the sky dome which is visi-

ble from the surface point, and E

⊥

(subscipt a for “at-

mosphere” or “ambient”) is the irradiance produced

by the sky dome on surface point with normal point-

ing straight into the sky dome and receiving light from

the entire dome. In our experiments the visibility frac-

tion V

is computed on a per point basis using the

scene geometry provided by the stereo camera, see

section 6.

The illumination model in this work consists of a

hemi-spherical sky dome of uniform radiance, and a

sun disk. The diameter of the sun disk as viewed from

earth is 0.53 degrees, (Dutr

e et al., 2003). The tech-

nique for estimating the irradiances (and hence the ra-

diances) of the sky and the sun directly from image

measurements represents the main contribution of this

paper. Our approach is in two steps: 1) detection of

dynamic shadows (cast by moving objects), and 2) us-

ing chromatic information from the detected shadows

to compute the radiance of the sky dome and the sun,

respectively.

Figure 2: Textured 3D scene mesh generated from stereo

disparity information from the image shown in ﬁgure 1.

Notice how well the main surfaces in the scene are recon-

structed.

5 SHADOW DETECTION

Existing work on single image shadow detection does

not really handle soft shadows, or requires manual

training. Example work includes (Nielsen and Mad-

sen, 2007; Finlayson et al., 2002; Salvador et al.,

OUTDOOR ILLUMINATION ESTIMATION IN IMAGE SEQUENCES FOR AUGMENTED REALITY

131

2004). Existing work on dynamic shadow detection

from image sequences either rely on a simplistic il-

lumination model (the grey world assumption which

is deﬁnitely not valid in outdoor scenes), or require

a high quality trained background model. Example

work includes (Huerta et al., 2009; Horprasert et al.,

1999; Kim et al., 2005; Chalidabhongse et al., 2003),

and a survey can be found in (Prati et al., 2003).

For this work we have developed a dynamic

shadow detection technique which does not rely on a

trained background model and utilizes the available

depth information. Figure 2 shows an example of

the 3D data provided by the Bumblebee camera (and

the accompanying API). In this section we brieﬂy de-

scribe the approach. For more detail and additional

experimental results, please refer to (Madsen et al.,

2009).

The shadow detection technique is based on image

differencing. A delayed frame (from time t − ∆t) is

substracted from the current frame (from time t) both

for color images and for stereo disparity images. If,

for a given pixel, the color image difference is nega-

tive in all three color channels (less light emited from

the point at time t than at time t − ∆t), and the dispar-

ity difference is zero (no change in depth), the pixel is

classiﬁed as a shadow candidate. If there is a change

in depth it is not a potential shadow candidate but

rather a pixel belonging to a moving object.

Choosing the length of the frame delay ∆t is not

critical. If set high (long delay) we achieve better abil-

ity to detect the whole shadow since the shadows cast

in the two frames are less likely to overlap. On the

other hand a long frame delay makes the system less

responsive to changes in the illumination conditions.

In the experiments reported here we have used a frame

delay of 0.5 seconds (the Bumblebee camera delivers

color and disparity images at a frame rate of 10 fps in

640x480 pixel resolution).

Figure 3 show the detected shadow candidates

corresponding to the image in ﬁgure 1. Here we have

used a ∆t of 10 seconds to give a better visual impres-

sion of detected shadows. Water poured onto surfaces

by the test person (to simulate rain) are also initially

classiﬁed as shadow candidates.

Further analysis of the shadow candidates is per-

formed in log chromaticity space. In log chromaticity

space, combining with the general pixel value expres-

sion from eq. (1), we get two chromaticity values per

pixel, r and b (using superscripts r/g/b to indicate

RGB color channel speciﬁc value):

r = log(P

)

= log(P

) −log(P

)

= log(c

) − log(c

) + log(ρ

) − log(ρ

) +

log(E

) − log(E

) (4)

Figure 3: Top: shadow candidate pixels in frame 139. Bot-

tom: veriﬁed shadow pixels after chromaticity analysis. No-

tice that water splashes are not classiﬁed as shadow pixels

demonstrating robustness to rain.

b = log(P

)

= log(c

) − log(c

) + log(ρ

) − log(ρ

) +

log(E

) − log(E

) (5)

If a pixel has been marked as shadow candidate it

means we have two versions of the same pixel, one

from time t and one from time t − ∆t. The color

channel values have changed for that pixel, which in

turn means that the pixel’s location in log chromatic-

ity space has moved. Basically two things can have

caused this: 1) sunlight at the surface point corre-

sponding to the pixel was blocked (shadow), or 2)

the surface changed albedo, e.g., became wet. Study-

ing the displacements in chromaticity space forms

the basis for the ﬁnal classiﬁcation of shadow pix-

els. This approach is inspired by (Marchand and

Onyango, 2000).

We assume that the camera constants c

r/g/b

did

not change during ∆t. If we hypothesize that the sur-

face albedos ρ

r/g/b

did not change:

∆r = r(t) − r(t − ∆t)

= log



(t)

(t − ∆t)



− log



(t)

(t − ∆t)



(6)

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

132

Figure 4: Left: per pixel normal map encoded as RGB val-

ues for the image in ﬁgure 1. Right: per pixel sky dome

visibility in the range 0 to 1.

∆b = log

(t)

(t − ∆t)

− log



(t)

(t − ∆t)



(7)

Thus, log chromaticity displacements of shadow

candidate pixels depend only on the change in inci-

dent irradiances, namely the various E

values (which

are of course unknown). This means that all shadow

pixels should exhibit displacements that are parallel

in log chromaticity space. If a pixel does not displace

in the same direction it must be because the albedo

changed (the constant albedo hypothesis is false and

eqs. 6 and 7 do not hold), e.g., the surface point

became wet, or it otherwise changed color. This is

utilized by selecting only the pixels whose displace-

ment orientation (computed as θ = arctan(∆b/∆r)) is

within a certain threshold of +90 degrees (a displace-

ment towards blue). We have used a threshold of 20

degrees. A shift towards blue is what is expected from

a surface point transitioning from being illuminated

by both the sun and sky, to only being illuminated by

the (blueish) sky. Figure 3 shows the shadow pixels

after the chromaticity analysis.

It must be noted that although the described meth-

ods work well on outdoor imagery, we do not need

perfect shadow detection. We just need robust, fast

detection of a population of high conﬁdence shadow

pixels to support the illumination estimation.

6 ILLUMINATION ESTIMATION

As described in section 4 the illumination model in

this work consists of a hemi-spherical sky dome of

uniform radiance, and a sun disk of uniform radiance.

The direction vector,

s, is computed procedurally us-

ing the method described in (Blanco-Muriel et al.,

2001).

Every detected shadow pixel provides some infor-

mation about the sun and sky irradiance in the scene.

At time t −∆t the pixel was not in shadow, and at time

t it is. At time t − ∆t, by combining eqs. (1) through

(3):

P(t − ∆t) = c · ρ · E

(t − ∆t) ·

= c · ρ ·



sun

(t − ∆t) + E

sky

(t − ∆t)



= c · ρ ·



~n ·

s · E

⊥

(t − ∆t)+

(t − ∆t) · E

⊥

(t − ∆t)



(8)

Here, sky dome visibility fraction, V

, is time de-

pendent since moving geometry in the scene may

change the fraction, especially for points in near prox-

imity of the shadow casting object. At time t the pixel

is in shadow and only the sky contributes to the irra-

diance:

P(t) = c · ρ ·V

(t) · E

⊥

(t) (9)

Eqs. (8) and (9) are per color channel. If we in-

troduce a quantity C which is the ratio of pixel value

in shadow to pixel value in sunlight, and assume ∆t

to be small enough that the sky and sun irradiances at

time t − ∆t equal those at time t:

C =

P(t)

P(t − ∆t)

(t) · E

⊥

(t)

~n ·

s · E

⊥

(t) +V

(t − ∆t) · E

⊥

(t)

(10)

Equation (10) is crucial. On the left hand side

the ratio C is based only on image measurements

(pixel values from the two frames), so this quantity

is known. On the right hand side~n is the surface point

normal, known from the stereo data;

s is the sun di-

rection vector, known from the GPS and the date and

time information; V

at time t and at time t − ∆t is the

sky dome visibility fraction, which can be computed

from the scene geometry data, see section 7 and ﬁgure

4. The only unknowns are the sun and sky irradiances.

Re-arranging eq. (10) yields:

⊥

(t) = E

⊥

(t)

(t) −C ·V

(t − ∆t)

~n ·

s ·C

(11)

Now the sun’s head-on irradiance is expressed in

terms of the sky irradiance times quantities from the

images and from scene geometry. Next we introduce

a constraint based on the white-balancing of the cam-

era. We assume that the camera is white-balanced.

This means that there must be some point in the scene

where the combined irradiances of the sun and sky is

color balanced, that is, the combined irradiance has

the same value, k, in all three color channels. Let ~n

be the normal of such a point and let V

be its sky

dome visibility fraction. In our experiments we have

used ~n

= [ 0 0 1 ] (so horizontal surfaces have

white-balanced illumination), and set V

to the av-

erage value of V

for all horizontal surface points in

OUTDOOR ILLUMINATION ESTIMATION IN IMAGE SEQUENCES FOR AUGMENTED REALITY

133

the scene. This white-balancing constraint says that

the sun and sky combined irradiance must sum to the

same number k in all color channels, expressible as:

k = ~n

s · E

⊥

(t) +V

(t) · E

⊥

(t) (12)

Combining eqs. (11) and (12) yields:

⊥

(t) + (~n

s/~n ·

s)(V

(t)/C −V

(t − ∆t))

(13)

To sum up, we could now, given the pixel values

at time t and time t − ∆t of only one shadow pixel,

compute the irradiance ratios C

r/g/b

in the three color

channel using eq. (10), insert into eq. (13) to get the

sky irradiance in three channels (up to a scale factor

of k), then insert into eq. (11) to get the sun irra-

diance in three channels (up to a scale factor of k).

To solve this overall scale problem we have chosen

the following approach. The input image is actually

measurements of scene radiances scaled by the cam-

era radiance-to-pixel-value proportionality constants

r/g/b

(see eq. (1)). We wish to scale the estimated

irradiances such that the reﬂected radiance of virtual

surface in the augmented scene is on the same bright-

ness level as the input image. k is the irradiance on

a horizontal surface in the scene. A suitable aver-

age albedo for general surfaces is 0.3 (earth’s aver-

age albedo), so the reﬂected radiance from such a sur-

face would be L

avg

= ρ

avg

· k · 1/π. Let P

avg

be the

average pixel value in the green channel of the input

image. We want the reﬂected radiance to equal the

average image intensity which means that we should

set k to:

k = πP

avg

/ρ (14)

By computing the scale factor this way the

augmented object changes brightness according to

changes to camera illumination sensitivity, e.g., if the

camera aperture is changed the luminance level of the

image changes, and the luminance level of the aug-

ment object changes with the same amount. This al-

lows us to enable the Automatic Gain Control (AGC)

of the camera so the method can be applied to very

long sequences with large variations in illumination.

This completes the theoretical background for the

illumination estimation from shadows. For render-

ing puporses we need the radiances of the sun and

the sky, not the irradiances. The radiance of the sky

is computed as L

(t) = E

⊥

(t)/π and the radiance of

the sun disk is computed as L

(t) = E

⊥

(t)/(2π · (1 −

cos(d/2))), where d = 0.53 degrees. The denomina-

tor is the solid angle subtended by a sun disk of 0.53

degree radius.

In the subsequent section we describe how the il-

lumination is estimated robustly from a whole popula-

tion of detected shadow pixels, not just from a single

one.

Figure 5: Dynamic shadow detection based on image dif-

ferencing (frames 180, 520, and 1741). These are the raw

detected shadow pixels. The spurious shadow pixels in the

top right of the images are removed with morphological op-

erations.

7 EXPERIMENTAL RESULTS

We have Matlab and C++ versions of the shadow de-

tection, and we have a Matlab implementation of the

illumination estimation.

In the C++ version shadow detection is running

at approx. 8 Hz on an Intel Core Duo 2 2.3 GHz

machine running Windows XP SP2, equipped with 2

GByte RAM. This framerate includes the stereo dis-

parity computations, and the construction of the ge-

ometry mesh from the depth data. Figure 5 illustrates

the shadow detection on some random frames from a

long image sequence with rapidly changing illumina-

tion conditions (partly overcast and very windy).

The expressions for estimating the illumination

conditions involve quantities relating to the geome-

try of the scene, namely the sky dome visibility frac-

tion V

and the surface normals. We construct trian-

gle meshes of the scene from the live disparity data

(an example mesh is shown in ﬁgure 2). The disparity

data is in 640 × 480 pixel resolution, which is mean

ﬁltered with a kernel size of 5 × 5. A 160 × 120 reg-

ular vertex grid is imposed on the disparity map and

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

134

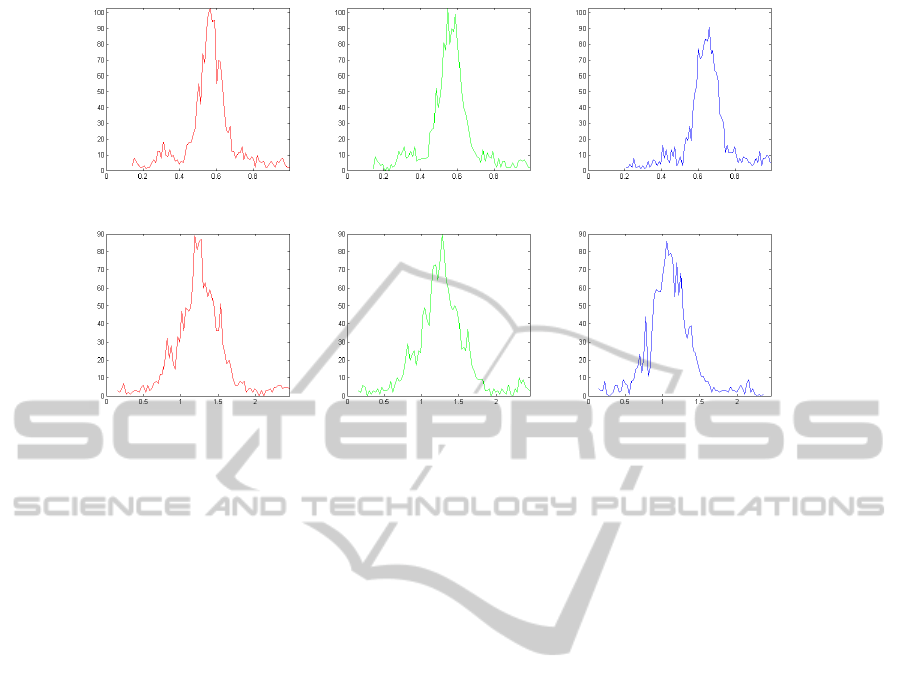
Figure 6: Top row: sky irradiance histograms for R, G, and B color channels. Bottom row: similar for sun irradiance. For

each histogram the horizontal axis shows the irradiance value with a scale factor k of 1, and the vertical axis is number of

pixels voting for that irradiance value. The histogram corresponds to the scene in ﬁgure 1.

the xyz position of each vertex is found by converting

the corresponding disparity value to depth and multi-

plying the pixel’s unit ray direction vector with that

depth. Two triangles are formed for every group of

4 vertices, resulting in 2 × 160 × 120 triangles, from

which triangles with normals almost perpendicular to

the viewing direction are discarded (typically trian-

gles that correspond to depth discontinuities). We get

per pixel normals by rendering the scene mesh using

a normal shader. For all renderings in this paper we

have used the RADIANCE rendering package, (Ward,

2009). Per pixel sky dome visibility is computed by

rendering irradiance values of the mesh (with mesh

albedo set to zero to avoid global illumination inter-

reﬂections) when illuminated with a sky dome of ra-

diance 1/π. Using this approach a normal pointing

straight into the sky and having un-occluded view of

the sky will receive an irradiance of 1, so the V

val-

ues will be in the range of 0 to 1 as desired. Figure 4

shows examples.

With per pixel geometry quantities, and with irra-

diance ratios C computed per detected shadow pixels

using eq. (10) we have a whole population of pixels

voting for the irradiances of the sky and the sun. Each

pixel, through eq. (13), contributes three channel val-

ues for the sky irradiance, and through eq. (11) for the

sun irradiance. This is computed for all shadow pixels

and histograms are formed of sky and sun irradiances

for each color channel, see ﬁgure 6.

From each of these histograms the most voted for

irradiance value is selected (histogram peak). Fu-

ture work includes either ﬁtting a Gaussian distribu-

tion, employ a mean shift algorithm, or to use Ran-

dom Sample Consencus (RANSAC), to ﬁnd the mean

more robustly than just taking peak value. In the ex-

ample in ﬁgure 6 the elected and ﬁnally scaled radi-

ance values are:

Sky radiance =



0.6548 0.6662 0.7446



Sun radiance =



60197 57295 51740



These numbers indicate primarily that the radi-

ance of the sun is 5 orders of magnitude higher than

that of the sky, which is consistent with the fact that

the sun’s subtended solid angle is 5 orders of magni-

tude smaller than a hemi-spherical sky dome, but as a

rule of thumb provides roughly the same irradiance as

the sky dome. Futhermore it can be noticed that the

sky’s color balance clearly is much more blue than

that of the sun. Figure 7 show more examples of ob-

jects rendered into scenes with illumination estimated

using the technique proposed in this paper.

Qualitatively, judging from ﬁgures 1 and 7 the

generated results are encouraging and the estimated

illumination conditions visually match the real scene

conditions sufﬁciently well to be convincing. Sub-

sequently we present some more controlled experi-

ments.

Synthetic Geometry, Synthetic Illumination

To test the technique’s performance on a scene for

which ground truth is available for the illumination

a synthetic scene has been rendered at two time in-

stances with a shadow casting pole moving from one

frame to another, see ﬁgure 8.

The ground truth sky radiance for the scene in ﬁg-

ure 8 is [

0.0700 0.1230 0.1740

] and the sun ra-

OUTDOOR ILLUMINATION ESTIMATION IN IMAGE SEQUENCES FOR AUGMENTED REALITY

135

Figure 7: Two examples of scenes with augmentations us-

ing the proposed technique for estimating illumination from

automatically detected shadows.

diance is [

72693 57178 42247

]. The estimated

sky radiance is [

0.0740 0.1297 0.1804

] and the

sun radiance is [

71687 55488 40622

], i.e., esti-

mations are within 5% of ground truth. A large pro-

portion of the deviation between ground truth and es-

timation result is believed to be due to inﬂuence from

indirect illumination (light reﬂecting from one surface

on to others), a phenomenon which is not taken intro

account by the applied two part illumination model

(sun and sky are assumed to be the only illuminants

in the scene).

Real Geometry, Synthetic Illumination

To test the performance under more realistic con-

ditions a pair of images were produced where the

dynamic objects are synthetic, but they are casting

shadow on real mesh geometry obtained from the

stereo camera. Figure 10 illustrates how these images

were generated.

The two frame image sequence thus generated

shows synthetically generated dynamic shadows on

real stereo geometry, using real camera images as

scene albedo, and yet we still have perfect ground

truth for the illumination, since the shadows are ren-

dered into the image.

Figure 8: Top: Two frames of a synthetic scene. Bottom:

detected dynamic shadow pixel population to be used for

illumination estimation.

The ground truth sky radiance for the scene in ﬁg-

ure 10 is [

1.0109 1.1644 1.2085

] and the sun ra-

diance is [

83082 81599 73854

]. The estimated

sky radiance is [

1.0658 1.2212 1.2614

] and the

sun radiance is [

88299 82764 79772

], i.e., esti-

mations are within roughly 5% of ground truth, except

for the red channel of the sun, which shows an error

of around 8%. Figure 11 shows an augmentation into

this semi-synthetic scene with the estimated illumina-

tion.

As in the previous all synthetic data example the

discrepancy is believed to be due to not explicitly

taking indirect illumination into account. For exam-

ple the sun’s red channel is somewhat over-estimated,

since in the shadow a lot of red-toned illumination

from the brick-walled building in the background of

ﬁgure 10 vanishes, and the assumed simpliﬁed illu-

mination model can only “explain” this by estimating

the sun’s red channel higher than it actually is.

Real Geometry, Real Illumination

As a ﬁnal example of the performance of the pre-

sented technique we return to the scene from ﬁgure

1, this time to another frame in the same sequence,

approximately 6 seconds earlier, see ﬁgure 9.

In ﬁgure 1 the sky radiance is estimated to

[

0.6548 0.6662 0.7446

] and the sun ra-

diance to [

60197 57295 51740

]. From

the frame in ﬁgure 9 the same values are es-

timated at [

0.6106 0.5874 0.6746

] and

[

68927 69784 62741

], respectively.

A signiﬁcant change in the estimated illumination

is noted on the quantitative level, although visually

the augmentation in the two cases is equally convinc-

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

136

Figure 9: Even with the shadow falling on completely dif-

ferent materials and with completely different geometric

properties the estimation illumination is comparable to that

of ﬁgure 1.

ing. The relatively large quantitative differences are,

in addition to the fact that this scene in particular in-

volves substantial indirect illumination contributions,

due to a lot of the pixels for the sunlit brick wall

are saturated in the red channel, i.e., exceed 255 in

pixel value. Naturally, such imperfect image expo-

sure makes it difﬁcult for the technique to estimate

proper results.

8 DISCUSSIONS AND FUTURE

WORK

The work described here is intended for sequences

of limited length (up to minutes). Futhermore it re-

quires the presence of dynamic objects to cast shad-

ows. We are developing additional techniques which

will be bootstrapped by the technique presented here,

but afterwards will be able to handle illumination es-

timation also in the absence of dynamic shadows, and

over very long image sequences.

The described technique is based on an assump-

tions that surfaces in the scene are predominantly

diffuse. While this is a fair assumption for much

outdoor material it is far from satisfactory to have

this constraint. We are presently pursuing analysis

of very long time sequences (full day, several days)

and are developing techniques to classify pixels that

do not agree with the majority on how the illumi-

nation in the scene changes. Those pixels are either

glossy/specular, a leaf has fallen on the surface, or

even snow. Our ambition is to develop techniques that

are robust enough to handle seasonal changes.

In the illumination estimation approach presented

in section 6 the illumination model does not take into

Figure 10: First row: frames 25 and 30 from real stereo im-

age sequence. Second row: detected shadow pixels from

trees moving in the wind. Third row: frame 30 augmented

with moving synthethic objects, using the illumination es-

timated from the shadow pixels in row two. Notice the re-

ﬂection of the sky in the artiﬁcial chrome ball to the left.

account the indirect global illumination contribution

from other surfaces in the scene. We are presently

rephrasing this work into a framework that does take

this into account. Moreover, we are investigating how

to employ a more realistic sky model than the uniform

radiance sky dome used here. A more realistic, non-

uniform sky dome could be the Perez model, (Perez

et al., 1993), or the Preetham model, (Preetham et al.,

1999).

The shadow detection is presently running at 8 Hz

including the stereo disparity computation. The illu-

mination estimation process itself poses no real com-

putational load, but the required ambient occlusion

map is not straight forward to obtain as this requires

some form of ray casting. Real-time global illumina-

tion methods are beginning to appear in the litterature,

OUTDOOR ILLUMINATION ESTIMATION IN IMAGE SEQUENCES FOR AUGMENTED REALITY

137

Figure 11: Augmentation into the scene were the illumina-

tion was estimated from the shadows of moving augmenta-

tions, which in turn were rendered into the original scene

with illumination estimated from the shadows of trees mov-

ing in the wind.

and for the use in conjunction with the work in this

paper we only need ambient occlusion factors for the

detected shadow pixels, not for the entire image.

9 CONCLUSIONS

We have presented a technique for adaptively estimat-

ing outdoor daylight conditions directly from video

imagery, and the technique has a potential for real-

time operation. The main scientiﬁc contribution is a

theoretically well-founded technique for estimation of

the radiances of sky and sun for a full outdoor illumi-

nation model directly from Low Dynamic Range im-

age sequences. The main contribution from a systems

point of view is a demonstration that automatic detec-

tion of dynamic shadows can feed information to the

illumination estimation.

The presented work an be used for rendering vir-

tual objects in Augmented Reality, but we conjecture

that illumination estimation can also make many clas-

sical computer vision techniques more robust to illu-

mination changes.

ACKNOWLEDGEMENTS

This work is funded by CoSPE project (project num-

ber 26-04-0171) and the BigBrother project (project

number 274-07-0264) under the Danish Research

Agency. This funding is gratefully acknowledged.

REFERENCES

Barsi, L., Szimary-Kalos, L., and Szecsi, L. (2005). Image-

based illumination on the gpu. Machine Graphics and

Graphics, 14(2):159 – 169.

Blanco-Muriel, M., Alarc

on-Padilla, D. C., L

opez-

Moratalla, T., and Lara-Coira, M. (2001). Computing

the solar vector. Solar Energy, 70(5):431 – 441.

Boivin, S. and Gagalowicz, A. (2001). Image-based ren-

dering of diffuse, specular and glossy surfaces from

a single image. In Proceedings: ACM SIGGRAPH

2001, pages 107–116.

Boivin, S. and Gagalowicz, A. (2002). Inverse rendering

from a single image. In Proceedings: First European

Conference on Color in Graphics, Images and Vision,

Poitiers, France, pages 268–277.

Cao, X., Shen, Y., Shah, M., and Foroosh, H. (2005). Sin-

gle view compositing with shadows. The Visual Com-

puter, pages 639 – 648.

Chalidabhongse, T., Kim, K., Harwood, D., and Davis, L.

(2003). A Perturbation Method for Evaluating Back-

ground Subtraction Algorithms. In Joint IEEE Inter-

national Workshop on Visual Surveillance and Perfor-

mance Evaluation of Tracking and Surveillance, Nice,

France.

Debevec, P. (1998). Rendering synthetic objects into real

scenes: Bridging traditional and image-based graph-

ics with global illumination and high dynamic range

photography. In Proceedings: SIGGRAPH 1998, Or-

lando, Florida, USA.

Debevec, P. (2002). Tutorial: Image-based lighting. IEEE

Computer Graphics and Applications, pages 26 – 34.

Debevec, P. and Malik, J. (1997). Recovering high dynamic

range radiance maps from photographs. In Proceed-

ings: SIGGRAPH 1997, Los Angeles, CA, USA.

Dutr

e, P., Bekaert, P., and Bala, K. (2003). Advanced

Global Illumination. A. K. Peters.

Finlayson, G., Hordley, S., and Drew, M. (2002). Remov-

ing shadows from images. In Heyden, A., Sparr, G.,

Nielsen, M., and Johansen, P., editors, Proceedings:

European Conference on Computer Vision, pages 823

– 836.

Gibson, S., Cook, J., Howard, T., and Hubbold, R. (2003).

Rapic shadow generation in real-world lighting envi-

ronments. In Proceedings: EuroGraphics Symposium

on Rendering, Leuwen, Belgium.

Hara, K., Nishino, K., and Ikeuchi, K. (2005). Light source

position and reﬂectance estimation from a single view

without the distant illumination assumption. IEEE

Trans. Pattern Anal. Mach. Intell., 27(4):493–505.

Havran, V., Smyk, M., Krawczyk, G., Myszkowski, K.,

and Seidel, H.-P. (2005). Importance Sampling for

Video Environment Maps. In Eurographics Sympo-

sium on Rendering 2005, pages 31–42,311, Konstanz,

Germany.

Horprasert, T., Harwood, D., and Davis, L. S. (1999). A sta-

tistical approach for real-time robust background sub-

traction and shadow detection. In Proceedings: IEEE

ICCV’99 FRAME-RATE Workshop, Kerkyra, Greece.

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

138

Huerta, I., Holte, M., Moeslund, T., and Gonz

alez, J.

(2009). Detection and removal of chromatic moving

shadows in surveillance scenarios. In Proceedings:

IEEE ICCV’09, Kyoto, Japan.

Jacobs, K. and Loscos, C. (2004). State of the art report on

classiﬁcation of illumination methods for mixed real-

ity. In EUROGRAPHICS, Grenoble, France.

Kanbara, M. and Yokoya, N. (2004). Real-time estimation

of light source environment for photorealistic aug-

mented reality. In Proceedings of the 17th ICPR,

Cambridge, United Kingdom, pages 911–914.

Kim, K., Chalidabhongse, T., Harwood, D., and Davis, L.

(2005). Real-time Foreground-Background Segmen-

tation using Codebook Model. Real-time Imaging,

11(3):167–256.

Loscos, C., Drettakis, G., and Robert, L. (2000). Interative

virtual relighting of real scenes. IEEE Transactions

on Visualization and Computer Graphics, 6(4):289 –

305.

Madsen, C. B. and Laursen, R. (2007). A scalable gpu-

based approach to shading and shadowing for photo-

realistic real-time augmented reality. In Proceedings:

International Conference on Graphics Theory and Ap-

plications, Barcelona, Spain, pages 252 – 261.

Madsen, C. B., Moeslund, T. B., Pal, A., and Balasubrama-

nian, S. (2009). Shadow detection in dynamic scenes

using dense stereo information and an outdoor illu-

mination model. In Koch, R. and Kolb, A., editors,

Proceedings: 3rd Workshop on Dynamic 3D Imaging,

in conjunction with Symposium of the German Associ-

ation for Pattern Recognition, Jena, Germany, pages

100 – 125.

Marchand, J. A. and Onyango, C. M. (2000). Shadow-

invariant classiﬁcation for scenes illuminated by day-

light. Journal of the Optical Society of America,

17(11):1952 – 1961.

Nielsen, M. and Madsen, C. (2007). Graph cut based seg-

mentation of soft shadows for seemless removal and

augmentation. In Proceedings: Scandinavian Con-

ference on Image Analysis, Aalborg, Denmark, pages

918 – 927.

Perez, R., Seals, R., and Michalsky, J. (1993). All-weather

model for sky luminance distribution–preliminary

conﬁguration and validation. Solar Energy, 50(3):235

– 245.

PointGrey (2009). Bumblebee XB3 stereo

camera, Point Grey Research, Inc.

www.ptgrey.com/products/bumblebee/index.html.

Prati, A., Mikic, I., Trivedi, M., and Cucchiara, R. (2003).

Detecting Moving Shadows: Algorithms and Evalua-

tion. IEEE Transactions on Pattern Analysis and Ma-

chine Intelligence, 25:918–923.

Preetham, A. J., Shirley, P., and Smits, B. (1999). A practi-

cal analytic model for daylight. In Proceedings of the

26th annual conference on Computer graphics and in-

teractive techniques, SIGGRAPH ’99, pages 91–100,

New York, NY, USA. ACM Press/Addison-Wesley

Publishing Co.

Salvador, E., Cavalarro, A., and Ebrahimi, T. (2004).

Shadow identiﬁcation and classiﬁcation using invari-

ant color models. Computer Vision and Image Under-

standing, 95:238 – 259.

Sato, I., Sato, Y., and Ikeuchi, K. (1999a). Acquiring a radi-

ance distribution to superimpose virtual objects onto

a real scene. IEEE Transactions on Visualization and

Computer Graphics, 5(1):1–12.

Sato, I., Sato, Y., and Ikeuchi, K. (1999b). Illumination dis-

tribution from brightness in shadows: adaptive esti-

mation of illumination distribution with unknown re-

ﬂectance properties in shadow regions. In Proceed-

ings: International Conference on Computer Vision,

pages 875–882.

Wang, Y. and Samaras, D. (2008). Estimation of multiple

directional illuminants from a single image. Image

Vision Computing, 26(9):1179–1195.

Ward, G. (2009). Radiance - Synthetic Imaging System. rad-

site.lbl.gov/radiance/.

Yu, Y., Debevec, P., Malik, J., and Hawkins, T. (1999).

Inverse global illumination: Recovering reﬂectance

models of real scenes from photographs. In Pro-

ceedings: SIGGRAPH 1999, Los Angeles, California,

USA, pages 215 – 224.

OUTDOOR ILLUMINATION ESTIMATION IN IMAGE SEQUENCES FOR AUGMENTED REALITY

139