A RAY TRACING BASED MODEL FOR 3D LADAR SYSTEMS

Tomas Chevalier

Division of Information systems, Swedish Defence Research Agency, FOI, Box 1165, 581 11 Linköping, Sweden

Keywords: 3D ladar, Laser radar, Sensor model, Ray tracing, BRDF, Atmosphere.

Abstract: This paper describes an approach to simulate long range laser based 3D imaging sensor systems. The model

is based on a ray tracing principle where a large amount of rays are sent from a sensor towards the scene.

The scene, the target surface, and the atmosphere affect the rays and the final light energy distribution is ac-

quired by a receiver, where sensor data is generated. The approach includes advanced descriptions of the

materials in the scene, and modeling of several effects in the atmosphere and the receiver electronics. A tur-

bulence model is included to achieve realistic long range simulations. Examples of simulations and corre-

sponding real world data collection are shown. Model validations are presented.

1 INTRODUCTION

During the last decade many sensors for 3D data

registration has emerged on the commercial market.

To determine optimal parameters for those sensors a

number of sensor system models have been devel-

oped along with these systems. At FOI (the Swedish

Defence Research Agency) the capability to model

various 3D ladar systems has been developed. A 3D

ladar (sometimes also called 3D laser radar) system

illuminates the scene with a laser and by scanning or

using a matrix detector it collects a 3D geometry

description of the scene, usually together with the

intensity response. Related works show some ap-

proaches and examples of modeling tools, but either

some important parts are ignored, as the atmosphere

simulations, or the models are too simplified.

The first step of simulation was focused on cor-

rectly retrieving the 3D geometry description, while

further efforts advanced the model to consider many

other aspects. Such aspects include the atmospheric

scintillations, the variation in the reflectance of sepa-

rate scene parts, the complete waveform generation,

and the capability to model several different sensor

system types for registering 3D data. The model

described in this paper is developed for monostatic

systems, where the transmitter and the receiver are

placed on the same platform. This is a common de-

sign for 3D ladar systems. It is mainly implemented

in Matlab, with some computationally heavy parts in

Java and C++.

This paper describes the model developed at FOI

and the physical-based framework that we use in our

development. Section 2 describes the different avail-

able sensor system types that have been considered

for modeling. Section 3 covers the model framework

and theories, especially for the atmosphere propaga-

tion of the laser beam. Details on validation efforts

are given in Section 4. Simulation examples follow

in Section 5 and we conclude the paper in Section 6.

1.1 Related Work

At the beginning of the sensor simulation history

some passive sensor models were effectively im-

plemented into graphics software and even in hard-

ware (Phong, 1975). The simulated sensors were

virtual cameras, and the algorithms were based on

fairly basic ray tracing methods.

These algorithms were developed into more

physically correctness and to include more advanced

sensors (Powell, 2000), who simulates FLIR sensors

and ladar sensors using graphics software.

To make the simulations more realistic and phys-

ically correct, more customized surface reflections

were required. Already in 1967 studies on the reflec-

tions from rough surfaces had been performed (Tor-

rance, 1967), and partly based on this, a physical

reflection model was developed in 1991 (He, 1991).

Some implications of non-Lambertian reflections for

machine vision was published in 1995 (Oren, 1995).

A large number of sensor modeling projects have

been published during the years and during the last

Chevalier T..

A RAY TRACING BASED MODEL FOR 3D LADAR SYSTEMS.

DOI: 10.5220/0003322700390048

In Proceedings of the International Conference on Computer Graphics Theory and Applications (GRAPP-2011), pages 39-48

ISBN: 978-989-8425-45-4

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

decade a number of 3D laser sensor models have

evolved. For instance the work behind a 3D imaging

laser scanner model was published in 2005 (Ortiz,

2005) and in 2006 BAE systems published their

work (Grasso, 2006) on a 3D imaging ladar sensor

model.

An American initiative to develop a sensor simu-

lation environment, called Irma, was started by the

Munitions Directorate at AFRL in 1980. At the be-

ginning the purpose was primarily passive IR (infra-

red) simulations, but now the program also includes

radar and ladar simulation capabilities. A number of

publications are showing this progress, for instance

(Savage, 2006; Savage, 2007; Savage, 2008), where

especially (Savage, 2006; Savage, 2007) covers the

ladar sensor development.

In parallel, DSTL began the development of a

simulation program, CameoSim (CAMouflage Elec-

tro-Optic SIMulation) (Moorhead, 2001), to primari-

ly simulate passive electro-optical sensors. This si-

mulation program is commercially available, but

unfortunately, the ladar module (which was sche-

duled to be working a couple of years ago) seems to

be postponed. Sources indicated further progress of

their burst illumination (BIL) simulation, and in

April 2008 they presented 3D imaging sensor simu-

lation based on CameoSim (Harvey, 2008).

A similar approach to the methods presented in

this report was performed by the Center for Ad-

vanced Imaging Ladar (CAIL), at the Utah State

University. Their ladar seeker model, LadarSim

(Budge, 2006), is also based on discrete ray tracing

as the approach presented in this paper, but differs in

some ways. As example they do not consider the

atmosphere, which is a major issue for Ladar system

performance, and their sub resolution pattern inside

each laser pulse is a hexagonal grid instead of the

common quadratic grid. LadarSim is not commer-

cially available and therefore not possible to com-

pare in detail to the model described in this paper.

There are also non-imaging simulation efforts

(Espinola, 2007; Grönwall, 2007), where the aim is

to assist in the sensor performance assessment,

without the need of sensor images.

2 3D LADAR SYSTEMS

Laser based 3D imaging systems can be of many

types, of which some are described in this section.

The most basic Time-of-Flight Laser Scanner that

sends out separate laser pulses and measure the time

to the returning echoes, the Burst Illumination Ladar

which camera controls the high-speed shutter syn-

chronized to the laser pulse to generate range slice

images, and finally the 3D Flash Ladar, which con-

tain a range sensing matrix detector to acquire com-

plete 3D data using only one single laser pulse.

2.1 Time-of-Flight Laser Scanner

The classic version of a 3D imaging laser system is

the Time-of-Flight (TOF) laser scanner, which

works as a range sensing single element detector

mechanically scanned over the scene to collect a

number of laser echoes, as in Figure 1. The direction

and range of each measurement is acquired, and by

using a common coordinate system for all echoes,

the data is registered together. Advanced versions of

this sensor system type allow the complete returning

waveforms to be acquired.

Figure 1: One-dimensional Time-of-Flight laser scanner

illustration. The sensor system to the left edge is illuminat-

ing the scene to the right (each line is one pulse), where

echoes are registered for each pulse, shown by circles and

crosses. Crosses illustrate multiple echoes from one pulse.

2.2 Burst Illumination Ladar

The Burst Illumination Ladar, also called Gated

Viewing system (Steinvall, 1999), consists of a short

pulsed laser, a high-speed shutter, and a camera.

This system uses an adjustable delay between the

transmitted laser pulse and the high-speed shutter,

while flooding the scene completely with a pulsed

laser. The adjustable delay is used for temporal

scanning, making it possible to register different

range “slices” (or range gates) of the scene, which

means to register light energy that is reflected to-

wards the sensor from a certain distance, see Figure

2. Due to the possibility to use standard cameras,

this sensor system type can have a very dense spatial

resolution, high frame rate, or prf (pulse repetition

frequency).

This sensor data needs post-processing to give

range values in each pixel. This processing is based

on stepping through a number of range slices and

detecting peaks for each pixel. If interpolation is

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

Fi r st p u l se

Second pulse

hird pulse

Figure 2: One-dimensional Burst Illumination Ladar sys-

tem illustration. The left edge of the top image shows the

sensor system flood illuminating the scene to the right,

where the spatial resolution is set by the camera. The

range dimension is binned by adjusting the delay between

the emitted pulse and the shutter in the detector. One emit-

ted pulse results in one registered slice, as shown in each

of the bottom figures. The gray scale color in the rectan-

gles illustrates the intensity in the echo, where white is

high intensity, and black is low intensity.

performed the depth resolution can be a lot better

than the distance between the slices (Andersson,

2006).

2.3 3D Flash Ladar

The 3D Flash Ladar system collects range data in a

detector element matrix at a reasonable good frame

rate. This makes it possible to register changes in a

scene in three dimensions. Some systems only

record range images while others record a complete

waveform in each pixel, currently at the cost of low

spatial resolution due to large sensor pixel elements.

Figure 3 shows how this sensor system type records

data.

This sensor system type is very interesting for fu-

ture applications, especially since the data is format-

ted as range images and common straight-forward

signal processing methods, like morphological oper-

ations, are applicable directly on the 3D data.

3 SENSOR DATA MODELING

All 3D ladar systems mentioned in Section 2 can be

modelled using the same theory and framework al-

though several parameters differ. This section de-

scribes the framework and main parts of the theory.

Figure 3: Two-dimensional 3D Flash Ladar system illu-

stration. The scene to the right is flood illuminated from

the left. The spatial resolution is set according to the de-

tector matrix. The range dimension is binned inside the

advanced detector elements, as shown in the bottom fig-

ure, where only one laser pulse is used to generate all the

data. The gray scale color in the rectangles illustrates the

intensity in the echo, where white is high intensity, and

black is low intensity.

3.1 Model Framework

The model framework is built on four separated sec-

tions of settings; the scene, the laser source, the at-

mosphere, and the receiver.

° The scene settings define the geometry of all the

objects in the scene, i.e. the physical environ-

ment that the sensor system will look at. It

should also contain links to material descriptions,

to allow advanced reflections according to meas-

ured material samples.

° The laser source settings define the way the

scene is illuminated; both temporally and spa-

tially.

° The atmosphere settings define the atmospheric

conditions such as the turbulence strength and

the aerial attenuation, see Section 3.4.

° The receiver settings define the receiver in the

modelled system, together with its optics. The

receiver spatial resolution sets the base resolution

used throughout the simulation. This is multi-

plied by a sub resolution, determining the ability

to image small details in the scene.

Each sub element is represented by a ray sent-

through the optics towards the scene. The propaga

A RAY TRACING BASED MODEL FOR 3D LADAR SYSTEMS

Target

speckles

MTF

opt

Quant

MTF

speckle

RON

A/D

× ×

Laser energy

distribution

Turbulence

scintillations

Scene /

Target

MTF

turb

Figure 4: The model framework. One example scene (a reference board used for the validation measurements) is illumi-

nated by a laser source, turbulence scintillations are multiplied and turbulence blurring effects are applied by convolution.

The right of the ‘Quant’-step contains the target speckle, the optics and the receiver effects. The contributions in this paper

are mainly on the atmospheric simulations, and the quick but accurate combination with MTFs to simulate several types of

signal disturbances.

tion of each ray is calculated in detail to detect inter-

sections in the scene. Each of these intersections

gives the information on which material is hit and in

which angles the light incidents and reflects. To-

gether with the laser spatial energy distribution, and

the atmospheric scintillation, this information is used

to determine the proportion of the transmitted light

that finally hits the sensor element surface. The

simulation framework is described in Figure 4,

where the scene is illuminated by a laser source and

affected by turbulence scintillations and blurring

effects (MTF

turb

). Further on, the signal energy is

quantized into photons (Quant) and blurred even

more by the receiver optics (MTF

opt

). The receiver

electronics defines the quantum efficiency (η

), the

dark current noise (I

), the Gain (G), and the read-

out-noise (RON). In the sensor we also see the target

speckle effects together with blurring (MTF

speckle

Finally the signal is converted into a digitally re-

corded data by an A/D-conversion. In the figure,

means element-wise multiplication, means con-

volution, and means element-wise addition.

This figure only shows the spatial part of the en-

ergies, even though the temporal parts are well con-

sidered in all these model steps. The temporal parts

are introduced by considering the scene as an im-

pulse response to the three-dimensional energy dis-

tribution of the laser illumination.

The model parts containing the main contribu-

tions of this paper; the material description, the at-

mosphere modeling, and the sensor data degrada-

tion, are described in the following subsections, to-

gether with a fundamental system transfer function

called the laser radar equation.

3.2 Laser Radar Equation

The one most fundamental relation these simulations

are based upon is the laser radar equation (Jelalian,

1992), that describes the relation between the trans-

mitted and the receiver energy as

aer

r T syst

PP e

ηρ

−

⎛⎞

=⋅ ⋅⋅ ⋅

⎜⎟

⎝⎠

(3-1)

It is derived from the well known radar equation

(Skolnik, 2008), and identification of the three parts

(to the right of P

) in the equation tells us that the

efficiency factor,

syst

, is the system efficiency. This

is followed by the (parenthesized) BRDF, see Sec-

tion 3.3, which consists of two factors; first the

BRDF [sr

-1

, and then the solid angle [sr] the re-

ceiver optics aperture covers as seen from the target

reflecting the beam. The last factor, e

-2

, is the two-

way aerial transmission due to aerosol particles in

the atmosphere. The laser radar equation is used to

attenuate each ray that passes through the atmos-

phere.

3.3 Material Reflections

To describe the surface reflection properties in detail

the BRDF (bi-directional reflection density func-

tion),

, is used. The BRDF describes how an inci-

dent beam spreads into different angles. Figure 5

shows a BRDF example, where the amplitude is the

portion of the energy that is reflected (per steradian)

into a specific angle when a light source illuminates

the surface from the direction parallel to the surface

normal. The full BRDF descriptor allows a three-

dimensional reflection distribution, but in our work

we simplify it by using a two-dimensional approxi-

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

mation as in Figure 5, since we model a monostatic

system. Also note that a specific BRDF is valid only

for one wavelength.

-50 0 50

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

Angle of incidence [deg]

BRDF [sr

A=0.3

B=0.4

m=0.5

s=0.3

Figure 5: A synthetic BRDF example with the amplitude

as a function of the reflected angle when the angle of inci-

dence is parallel to the surface normal. Both a smooth and

a noisy version are shown.

Even though BRDF measurements for several

materials are available, we also need to model the

BRDF analytically, to approximate the reflection

properties for some materials. With some standard

assumptions the BRDF definition (Steinvall, 1997)

follows

cos cos

isis

dP P

dSurface Radiance

Surface Irradiance P P

ΩΩ

==≈

(3-2)

where the variables are depicted in Figure 6. The

reflected solid angle is given by

. The incident and

scattered light flux are represented by P

and P

. Fi-

nally, the angles of incidence and scattering are

represented by

and

, respectively. In the monos-

tatic system case, the angle of incidence coincides

with the angle of the relevant scattering light, which

gives us

There are advanced models to estimate the

BRDF, which relate it to roughness, surface slope,

correlation lengths, refractive index etc., but many

of them tend to get unnecessary complicated. Some

interesting simplified models have been published,

and one of them, a one-dimensional version for mo-

nostatic systems, (Steinvall, 2000) is given by

()

ρρρ

diffspec

cos

tan

+=+=

−

(3-3)

A and B are constants describing the relation be-

tween the specular and diffuse reflection. Specul

reflection is the strong reflection where

and

dΩ

Figure 6: Description of the variables used in the BRDF

definition. P shows the light flux while θ/φ are angles. The

subscript s means scattering/emitting and i means incident.

is the solid angle. The figure is adapted from Steinvall

(Steinvall, 2000).

. It can be recognized as the peak in the middle

of Figure 5. The diffuse reflection supports the base

reflection below the peak in the middle and covers

reflection into almost any direction. The local slope

is represented by s, and m is a parameter describing

the diffuse surface. The angles of incidence and ref-

lection are equal and represented by

The BRDF is measured per steradian [sr

-1

which is defined as the solid angle of the reflected

light. The following equation calculates the solid

angle [sr] of the receiver aperture that is collecting

the returning signal

Ω=

(3-4)

where

is the receiver aperture radius and R is the

range to the target.

The practical use of the BRDF in the model in-

cludes a lookup table that connects the ray inter-

sected surface, to a material in the database. If the

material has measured BRDF data, that is used, oth-

erwise a parameterized version is used to calculate

the reflection according to equation (3-3).

3.4 Atmosphere Modeling

The turbulence in the atmosphere makes the propa-

gating light deviate from the straight path, because

of the variations in the aerial refractive index. This

makes the signal of even a flat energy distribution

from the transmitter to stochastically fluctuate at the

range of the scene, as can be seen in Figure 7, where

the square middle target is a unicolored reference

board. The image show the target board, as seen

A RAY TRACING BASED MODEL FOR 3D LADAR SYSTEMS

from the receiver close to the laser (two-way propa-

gation).

Figure 7: Two-way turbulence scintillations example at

SWIR wavelength, with C

=1.15⋅10

-14

. The image was

acquired at 1km range with a FOI developed Burst Illumi-

nation Ladar system.

A very accurate way to simulate this behavior of

the propagating beam is to use phase screens (An-

drews, 1998; Andrews, 2001). However, simulations

using phase screens are computationally very heavy.

We have near real-time demands on our simulations

and therefore we have chosen to use an approxima-

tion. In our simulation, the atmospheric effects are

divided into the following approximately indepen-

dent parts, where the theories are adapted from An-

drews (Andrews, 1998; Andrews, 2001).

A. The beam Broadening

, depends on turbulence

strength (

) and the wavelength. It affects the

spreading of the laser energy distribution that il-

luminates the scene.

B. The Turbulence Scintillations

. The engineering

approach used in the model is described in Sec-

tion 3.4.1. The scintillation pattern is primarily

based on a probability density function and a

cell size equation, which describes the spatial

pattern scale. The scintillations are multiplied to

the laser energy as can be seen in Figure 4.

C. The Aerial Attenuation

, which makes the pulse

energy decrease as the range increases. This is

due to smoke, fog, rain, and other particles in

the air, and is a factor in the laser radar equation

(3-1).

D. The Beam Wandering

. The laser beam optical

axis is randomly deflected by the turbulence in

the air as it propagates through the atmosphere.

This effect introduces a displacement of the

energy returning from the scene.

E. The Distortion and Blurring effect

, which can

be seen in the images in Figure 7. A simplified

way of modeling this is by using MTF (modula-

tion transfer function) to blur the image. This

corresponds to the MTF used in passive im-

agery, since it can be regarded as a one-way ef-

fect for the atmospheric propagation from the

target into the receiver optics. The MTF is ap-

plied by convolution.

The turbulence strength (

) varies slowly over

the day and reaches maximum at about noon, while

the lowest values occur close to sunset and sunrise.

This derives from the temperature gradient and wind

velocity, which usually are lower at night, especially

close to the shift between day and night. Close to the

ground the turbulence is stronger than high up in the

atmosphere.

3.4.1 Turbulence Scintillations

Statistically a distribution of intensities given as a

pdf (probability density function) can be determined

mathematically, according to equation (3-5). Even a

turbulence cell size can be determined. Using these

data a randomized turbulence scintillation pattern

can be determined, as the example in Figure 8.

Figure 8: Simulated turbulence scintillation example ac-

cording to equation (3-5).

The turbulence scintillation pdf during weak tur-

bulence conditions is described (Andrews, 2001) by

ln ln

exp ln( ) 2

turb I I

σσ

πσ

⎛⎞

⎜⎟

=−+

⎜⎟

⋅

⎝⎠

(3-5)

The pdf is based on the log-intensity variance,

lnI

, which depends on the target resolution as seen

from the receiver, on the turbulence strength, and on

the light wavelength.

The turbulence cell radius,

, is determined in

relation to the spatial coherence radius of the current

turbulence condition (Andrews, 2001) as in equation

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

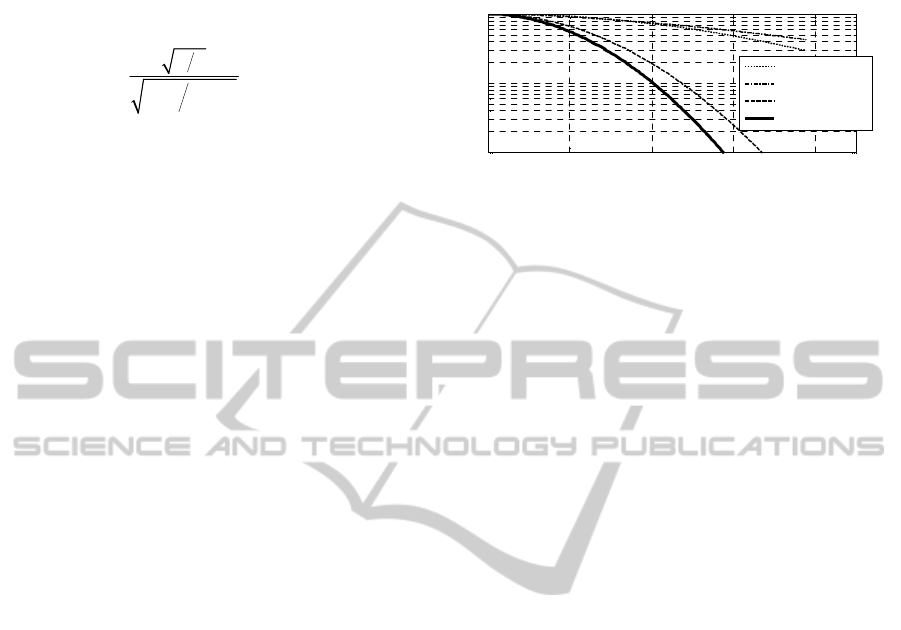
(3-6), where R is the range, k is the wave number

and

is the spatial coherence radius. This turbu-

lence cell radius is then used to spatially scale the

simulated turbulence scintillation.

()

(3-6)

To generate the spatial intensity distribution, as

the example in Figure 8, theory from Harris (Harris,

1995) is used as proposed by Letalick (Letalick,

2001). A randomized phase grid is generated, with

rectangular distribution (which is used by Goodman

(Goodman, 1984) in difference to Harris who uses

Gaussian distribution). This random field is multip-

lied by a Gaussian function corresponding to a field

distribution for the laser beam (TEM

). The Fourier

transform of the resulting matrix, the aperture func-

tion, gives the speckle field in the far field. By ad-

justing the spatial scale of the random noise and the

diameter of the Gaussian field distribution, different

scales and amplitudes for the speckle distribution

can be achieved. In this way the speckle field can be

matched to the probability density function in equa-

tion (3-5) and the turbulence cell size in (3-6).

3.5 Sensor Data Degradation

Several parts of the model cover sensor data degra-

dation. The problem is not to simulate perfect undis-

turbed data, but to catch the most important degrad-

ing effects of the atmosphere, the scene and the sen-

sor.

There already exist well described theories for

sensor degradation of passive imaging, using MTF

(modulation transfer function). This MTF is applied

to passive imagery to decrease the effective resolu-

tion in a system, and can be separated into several

parts, where the total system MTF is a multiplication

of all separate MTFs;

MTF

speckle

for the speckle lim-

ited resolution,

MTF

opt

for the diffraction limited

(optical) resolution and

MTF

turb

for the turbulence

limited resolution. The MTF are applied on the sen-

sor data by convolution. As can be seen in Figure 9

the limiting MTF can be determined. The figure

shows one-dimensional MTFs, even though the

simulations are calculated in two dimensions, with

radial symmetry.

The receiver unit contains the conversion from

photons to a digital signal. This process introduces

noise in many ways, for instance by the A/D-

conversion quantization, the dark current back-

ground noise, and the read-out noise in the sensor

elements. This is modelled according to the model

structure in Figure 4.

0 20 40 60 80

-2

-1

spatial frequency [cyc/mrad]

Target speckle

Turbulence

Optics

Total

Figure 9: One system MTF example, where the optics is

the limiting MTF and affects the total MTF the most.

4 SPATIAL DISTRIBUTION

VALIDATION

This section describes the validation procedures and

results for the spatial energy distribution. The model

of the spatial energy distribution as a function of

different turbulence levels is compared to outdoor

measurements. First we validate the pdf of the en-

ergy distribution along with its cell size. Then we

estimate the accuracy in the total system noise.

The first part is done using measurements at 1km

range at weak and medium turbulence. The system

(used for both measurements and simulations) is a

burst illumination system at 532 nm. As can be seen

in Figure 10, the visual resemblance is quite good

between the measured (top row) and the simulated

(bottom row) images. The correspondence between

the energy distributions (histograms using all data in

the images) is shown in the bottom row of the figure,

where the solid line is the measured data, and the

dashed blue line is the simulated data. The cell size

is hard to measure exactly, but for this example the

simulated cell size was about 16 pixels and the

measured cell size was about 14 pixels, which we

consider to be within reasonable interval.

The same data collection was used for the second

part of the validation. Figure 11 show the chosen

profile that was compared for a set of data and cor-

responding simulations. The white line in the top

figure is chosen as the validation profile and it was

compared between the measured and the simulated

data as can be seen in the lower figure. The bias and

the gain was compared in the complete data set and

showed to fit quite well.

A RAY TRACING BASED MODEL FOR 3D LADAR SYSTEMS

50 100 150 200 250

500

1000

1500

Real data

Simulated data

Figure 10: Validation of spatial energy distribution, where

the top row is measured data on a reference board and the

middle row is the simulated corresponding data. The bot-

tom row shows a comparison between the energy distribu-

tions (histograms of all image data in the top images),

where the measured data is shown with solid black line

and simulated with dashed blue line.

0 20 40 60 80 100 120 140

100

150

200

250

Real data

Simulated data

Figure 11: One validation example, where the profile

marked with the white line in the top simulated image is

shown in the bottom. The true measured profile is shown

as the dashed line.

5 EXAMPLES

The flexible capabilities of the model are shown

with some examples; B

urst Illumination Ladar, 3D

Flash Ladar,

and Range Profiling Ladar.

5.1 Burst Illumination Ladar

Parameters for a Burst Illumination Ladar were set

up to validate the spatially high resolved turbulence

effects. The example in Figure 10 shows measured

data as well as simulated data from a Burst Illumina-

tion Ladar system with the target being a reference

resolution board at 1 km range.

5.2 3D Flash Ladar

The currently most advanced 3D imaging sensor

system, the 3D Flash Ladar, was modelled including

the range detection in each pixel, which resulted in a

set of points (128

×128) from each frame. The simu-

lations included a sensor movement during data cap-

ture, and the registered data can be seen in Figure

12.

Figure 12: Simulated 3D Flash Ladar example. The target

vehicle on top row is measured from a number of angles,

in the environment seen in the middle row, and the data is

globally registered in a common coordinate system, as

shown on bottom row.

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

The top row shows the target vehicle which was

placed on ground in a forested scene as seen on the

middle row. The bottom row shows the globally

registered points from five frames, collected from

separate viewing directions.

5.3 Range Profiling Ladar

The capability to simulate waveforms is illustrated

by this one dimensional simulation, where an air-

craft, JAS 39 Gripen, is flood illuminated with a

single laser beam, and all returning energy is col-

lected into one single waveform. The top row in

Figure 13 shows the target air craft that is illumi-

nated from the left and the bottom row shows the

returning echo.

150 200 250 300 350 400 45

Figure 13: Range profiling simulation of the JAS 39 Gri-

pen. The top row shows the target that is flood illuminated

with a laser from the left, and the returning echo wave-

form is shown below. Note the peak which corresponds to

the engine covers that were present at the aircraft model.

6 CONCLUSIONS

We have developed a model to simulate complex 3D

ladar systems. It is a model that combines imaging

of advanced scenario setups with atmospheric turbu-

lence modeling as well as allowing degrading sensor

effects to affect the resulting data. The simulation

framework is divided into four fundamental parts;

the scene, the laser source, the atmosphere and the

receiver.

Earlier models developed for ladar simulations

mostly lack the capability to simulate the atmos-

phere, or is not flexible enough to simulate several

types of systems. A key contribution with this paper

is therefore the atmospheric turbulence modeling

that fits a fairly simple scintillation pattern to the

advanced theory for laser beam propagation. We

have also presented that this turbulence modeling

can be applied to a complete system model that is

flexible and capable of modeling a number of sensor

system types. Finally, we have shown that the use of

advanced material reflections (BRDF) can be ap-

plied upon the commonly used ray tracing methods.

We have successfully validated some parts of the

model but also identified difficulties to validate the

atmospheric simulations due to some stochastically

varying entities. One important issue causing this

problem is the lack of measurement data, since some

atmospheric parameters uncontrollably varies during

acquisition. Another important issue is that the

knowledge about the parameters inside many of the

sensor systems are proprietary information and

therefore confidential.

REFERENCES

Andersson, P., 2006. Long range 3D imaging using range

gated laser radar images. Optical Engineering, 45.

Andrews, L. C. & Phillips, R. L., 1998. Laser Beam

Propagation through Random Media, Bellingham,

Washington, USA, SPIE Press.

Andrews, L. C., Phillips, R. L. & Hopen, C. Y., 2001.

Laser Beam Scinitillation with Applications, Belling-

ham, Washinton, USA, SPIE Press.

Budge, S., Leishman, B. & Pack, R., 2006. Simulation and

modeling of return waveforms from a ladar beam

footprint in USU LadarSIM. SPIE Defence & Security,

Laser Radar Technology and Applications XI, Or-

lando, FL, USA, 62140N.

Espinola, R. L., Teaney, B., Nguyen, Q., Jacobs, E. L.,

Halford, C. E. & Tofsted, D. H., 2007. Active imaging

system performance model for target acquisition. SPIE

Defense & Security Symposium, Infrared Imaging Sys-

tems: Design, Analysis, Modeling, and Testing XVIII,

Orlando, FL, USA, 65430T.

Goodman, J. W., 1984. Statistical Properties of Laser

Speckle Patterns. IN DAINTY, J. C. (Ed.) Topics in

Applied Physics: Laser Speckle and Related Phenom-

ena. 2nd ed., Springer-Verlag.

Grasso, R. J., Dippel, G. F. & Russo, L. E., 2006. A model

and simulation to predict 3D imaging LADAR sensor

systems performance in real-world type environments.

SPIE Atmospheric Optical Modeling, Measurement,

and Simulation II,, 63030H.

Grönwall, C., Steinvall, O., Gustafsson, F. & Chevalier,

T., 2007. Influence of laser radar sensor parameters on

range-measurement and shape-fitting uncertainties.

Optical Engineering, 46, 106201.

A RAY TRACING BASED MODEL FOR 3D LADAR SYSTEMS

Harris, M., 1995. Light-field fluctuations in space and

time Contemporary Physics, 36, 215-233.

Harvey, C., Wood, J., Randall, P., Watson, G. & Smith,

G., 2008. Simulation of a new 3D imaging sensor for

identifying difficult military targets. SPIE Defense &

Security Symposium, Laser Radar Technology and

Applications XIII, Orlando, FL, USA, 69500I.

He, X. E., Torrance, K. E., Sillion, F. X. & Greenberg, D.

P., 1991. A Comprehensive Physical Model for Light

Reflection. 18th annual conference on Computer

graphics and interactive techniques, 175-186.

Jelalian, A. V., 1992. Laser Radar System, Norwood, MA,

Artech House.

Letalick, D., Carlsson (later Grönwall), C. & Karlsson, C.,

2001. A speckle model for laser vibrometry. 11th Co-

herent laser radar conference, Great Malvern, UK,

44-47.

Moorhead, I. R., Gilmore, M. A., Houlbrook, A. W., Ox-

ford, D. E., Filbee, D. R., Stroud, C. A., Hutchings, G.

& Kirk, A., 2001. CAMEO-SIM: a physics-based

broadband scene simulation tool for assessment of

camouflage, concealment, and deception methodolo-

gies. Optical Engineering 40, 1896-1905.

Oren, M. & Nayar, S. K., 1995. Generalization of the

Lambertian model and implications for machine vi-

sion. International Journal of Computer Vision 14,

227-251.

Ortiz, S., Diaz-Caro, J. & Pareja, R., 2005. Radiometric

Modeling of a 3D Imaging Laser Scanner. SPIE Elec-

tro-Optical and Infrared Systems: Technology and

Applications II, 598709.

Phong, B. T., 1975. Illumination for Computer generated

pictures. Communications of the ACM, 18, 311-317.

Powell, G., Martin, R., Marshall, D. & Markham, K.,

2000. Simulation of FLIR and LADAR data using

graphics animation software. The Eighth Pacific Con-

ference on Computer Graphics and Applications,

Hong Kong, 126-134.

Savage, J., Coker, C., Edwards, D., Thai, B., Aboutalib,

O., Chow, A., Yamaoka, N. & Kim, C., 2006. Irma 5.1

multi-sensor signature prediction model. SPIE Defense

& Security Symposium, Targets & Backgrounds XII:

Characterization and Representation, Orlando, FL,

USA, 6239OC.

Savage, J., Coker, C., Thai, B., Aboutalib, O., Chow, A.,

Yamaoka, N. & Kim, C., 2007. Irma 5.2 multi-sensor

signature prediction model SPIE Defense & Security

Symposium, Modeling and Simulation for Military

Operations II, Orlando, FL, USA, 656403.

Savage, J., Coker, C., Thai, B., Aboutalib, O. & Pau, J.,

2008. Irma 5.2 multi-sensor signature prediction

model SPIE Defense & Security Symposium, Model-

ing and Simulation for Military Operations III, Or-

lando, FL, USA, 69650A.

Skolnik, M. I., 2008. Radar Handbook, New York, USA,

McGraw-Hill.

Steinvall, O., 1997. Theory for laser systems performance

modelling. Linköping, FOA. FOA-R--97-00599-612--

SE.

Steinvall, O., Olsson, H., Bolander, G., Carlsson (later

Grönwall), C. & Letalick, D., 1999. Gated Viewing

for target detection and target recognition. SPIE Laser

Radar Technology and Applications IV, Orlando, FL,

USA, 432-448.

Steinvall, O., 2000. Effects of target shape and reflection

on laser radar cross sections. Applied Optics, 39, 4381-

4391.

Torrance, K. E. & Sparrow, E. M., 1967. Theory for off-

specular reflection from roughened surfaces. Journal

of the Optical Society of America, 57, 1105-1114.

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications