ILLUMINATION CORRECTION FOR IMAGE STITCHING

Sascha Klement, Fabian Timm and Erhardt Barth

Institute for Neuro- and Bioinformatics, University of L

ubeck, Ratzeburger Allee 160, 23538 L

ubeck, Germany

Pattern Recognition Company GmbH, Innovations Campus L

ubeck, Maria-Goeppert-Straße 1, 23562 L

ubeck, Germany

Keywords:

Illumination correction, Texture mapping, Image stitching.

Abstract:

Inhomogeneous illumination occurs in nearly every image acquisition system and can hardly be avoided sim-

ply by improving the quality of the hardware and the optics. Therefore, software solutions are needed to

correct for inhomogeneities, which are particularly visible when combining single images to larger mosaics,

e.g. when wrapping textures onto surfaces. Various methods to remove smoothly varying image gradients

are available, but often produce artifacts at the image boundary. We present a novel correction method for

compensating these artifacts based on the Gaussian pyramid and an appropriate extrapolation of the image

boundary. Our framework provides various extrapolation methods and reduces the illumination correction

error signiﬁcantly. Moreover, the correction is done in real-time for high-resolution images and is part of an

application for virtual material design.

1 INTRODUCTION

Digital images in many ways suffer from deﬁciencies

of the hardware that was used for capturing the image,

including sensor, lenses, and illumination. Even with

a perfect sensor, a lens without aberrations and a per-

fectly homogeneous illumination, the image may still

show an intensity falloff towards the corners of the

image due to natural vignetting. In general, the illu-

mination inhomogeneity is much more complex (Ag-

garwal et al., 2001) and cannot be described with a

simple model.

In various applications, such as 3D-texture map-

ping, aerial photography or astronomy, illumination

gradients need to be removed when creating image

mosaics. Without correction, transitions between sin-

gle images would clearly be visible. These artifacts

might mislead further image processing or pattern

recognition systems, and therefore need to be reduced

to a minimum.

The problem of illumination correction has been

addressed by many authors, often with respect to a

speciﬁc illumination artifact. Vignetting correction

methods have been proposed e.g. in (Zheng et al.,

2009) and (Kim and Pollefeys, 2008). In mag-

netic resonance imaging a method as been proposed

based on information minimisation where the cor-

rection components are modelled as combinations of

smoothly varying basis functions (Likar et al., 2001).

In face recognition, methods for illumination com-

pensation have been proposed as a preprocessing step

(Adini et al., 1997; Levine et al., 2004), primarily to

ﬁnd a more invariant face representation. Recently, a

non-parametric shading correction method has been

proposed in (Reyes-Aldasoro, 2009). An overview

of stitching and blending methods can be found in

(Levin et al., 2004).

We aim for an illumination correction method that

not only removes inhomogeneities correctly without

boundary artifacts, but which is also qualiﬁed for

real-time applications such as virtual material design.

Thus, we focus on a simple method based on lowpass

ﬁltering using Gaussian pyramids and appropriate im-

age extrapolation to avoid boundary artifacts. First,

we give a short introduction to Gaussian pyramids

to show why boundary artifacts may occur. Then,

we propose a framework that covers various standard

boundary conditions for ﬁltering and mention suitable

extrapolation functions. Finally, we show the perfor-

mance of our method with some practical examples.

2 THE GAUSSIAN PYRAMID

For more than two decades, pyramid methods have

been used for image processing tasks such as image

enhancement, compression, interpolation and extrap-

Klement S., Timm F. and Barth E..

ILLUMINATION CORRECTION FOR IMAGE STITCHING.

DOI: 10.5220/0003323300810086

In Proceedings of the International Conference on Imaging Theory and Applications and International Conference on Information Visualization Theory

and Applications (IMAGAPP-2011), pages 81-86

ISBN: 978-989-8425-46-1

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

olation of missing image data and numerous others

(Ogden et al., 1985).

Given a gray-valued input image with intensity

values G

(x, y) at discrete locations x ∈ [0, m − 1] and

y ∈ [0, n − 1] the Gaussian pyramid is an efﬁcient data

structure for spectral decomposition as follows. For

each level i the image G

(x, y) is lowpass ﬁltered and

downsampled by a factor of two to produce the im-

age G

i+1

(x, y). This is commonly referred to as the

Reduce operation.

i+1

= Reduce(G

) = (↓ 2)(h ∗ G

) with

(↓ 2) f (x, y) = f (2x, 2y).

This is done successively up to a certain level l. Then,

the Expand operation is applied successively to get an

image with the same size as G

, but containing only

the frequency components of G

i−1

= Expand(G

) = 4h ∗ ((↑ 2)G

The weighting function h is often called the gener-

ating kernel and is commonly chosen to be a 5-by-

5 binomial ﬁlter to approximate the Gaussian. This

method for computing the low frequency components

of the input image is obviously more efﬁcient than

direct convolution with a large ﬁlter but also more ef-

ﬁcient than using standard FFT (Adelson et al., 1984).

Finally, we need to decide how the image data is

extended when ﬁltering boundary pixels. This is the

critical step where boundary artifacts occur. In the

following, we present a general framework that cov-

ers not only the extrapolation conditions for rectangu-

lar images, but also arbitrary image shapes that occur,

e.g., during image segmentation.

3 BOUNDARY EXTRAPOLATION

Since the ﬁltering operation is deﬁned as

( f ∗ h)(x, y) =

+∞

∑

i=−∞

+∞

∑

j=−∞

h(i, j) f (x − i, y − j)

the image needs to be extended by two pixels — ei-

ther virtually or explicitly — in each direction when

using 5-by-5 ﬁlters. Commonly, the pixels outside

the image are set to a constant value or to the value

of the nearest boundary pixel (replicate boundary) or

are computed by assuming a periodic image (circular

boundary).

Given the input image f (x, y) with x ∈ [0, m − 1]

and y ∈ [0, n − 1] we seek an extended image f

(x, y)

with x ∈ [−2, m + 1] and y ∈ [−2, n + 1]. Next, we

deﬁne for each pixel (x, y) a set of pixels

x,y



, p



x,y

i=1

that have an inﬂuence on the intensity at (x, y) in the

extended image. Finally, the function g

x,y

(x, y) de-

ﬁnes how to calculate the intensity at (x, y) from the

intensities of the set of pixels P

x,y

. Thus, we get

(x, y) =







f (x, y) if x ∈ [0, m − 1]

and y ∈ [0, n − 1]

x,y

(x, y) otherwise.

(1)

For convenience, we use g(x, y) instead of g

x,y

(x, y).

Next, we show how the standard boundary conditions

— replicate and circular — as well as different ex-

trapolation methods ﬁt into this framework.

3.1 Replicate Boundary

Assuming a replicate boundary, the intensity values of

pixels outside of the image equal those of the nearest

boundary pixel:

rep

x,y

(



, p





= min(max(x, 0), m − 1)

= min(max(y, 0), n − 1)

)

Thus,



rep

x,y



= 1 for all x and y, and g

rep

(x, y) =

f (p

, p

). Analogously, a circular boundary condi-

tion can be deﬁned:

circ

x,y

(



, p





= x mod m

= y mod n

)

Again, |P

circ

x,y

| = 1 for all x and y and

circ

(x, y) = f (p

, p

3.2 Simple Linear Extrapolation

Both replicate and circular boundary assumptions, are

no valid assumptions when modelling illumination

gradients. In almost all cases of natural illumina-

tion inhomogeneity the intensity gradient will con-

tinue smoothly outside of the image bounds. When

compensating for vignetting, the application of repli-

cate or circular boundary assumptions will overesti-

mate the intensity gradient at the boundary.

A ﬁrst step towards more realistic boundary as-

sumptions involves simple linear extrapolation of the

intensity values at the boundary. The gradient is

the difference between a boundary pixel and its next

neighbour towards the centre of the image. Mathe-

matically, this can be expressed in the following way:

lin

x,y



, p





, p



with

= min(max(x, 0), m − 1)

= min(max(y, 0), n − 1)

= min(max(x, 1), m − 2)

= min(max(y, 1), n − 2) and

IMAGAPP 2011 - International Conference on Imaging Theory and Applications

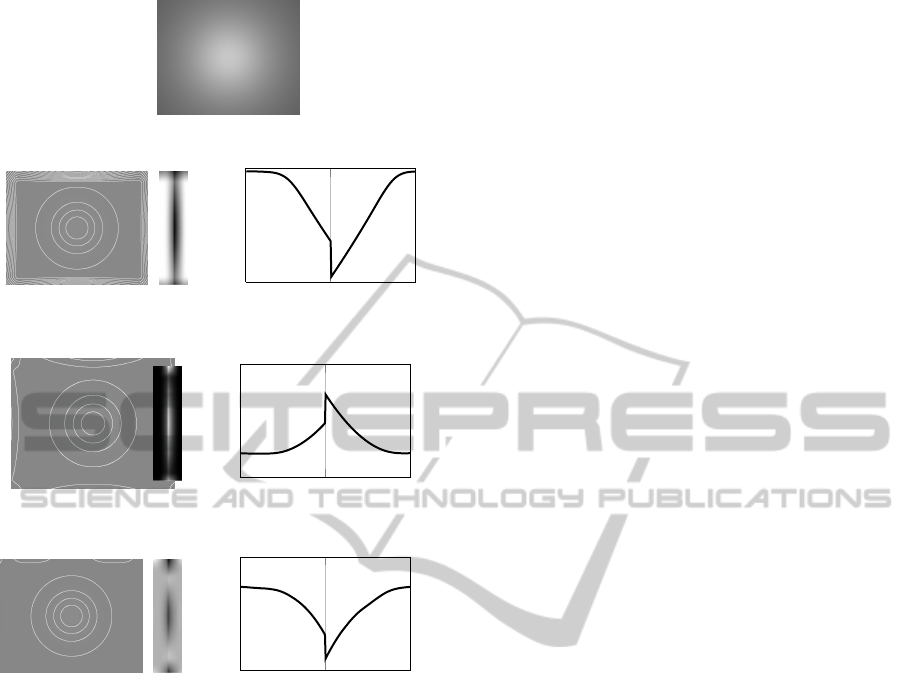
(a) Synthetic input image (natural vignetting).

right border left border

127

137

(b) Replicate condition.

right border left border

135

138

right border left border

135

136

(d) Polynomial extrapolation.

Figure 1: Illumination correction without texture. The in-

tensity levels of the corrected images (left) are emphasised

with contours. Additionally, an image transition (middle

column, 128 pixels from each side, intensity stretched to

full range) and the intensity across the middle row (right)

are shown. Note the different scales on the y-axis and that

the boundary artifacts are reduced.

lin

(x, y) = f



, p





, p



− f



, p







x − p

y − p





where k · k

denotes the Manhattan distance. This

modiﬁcation improves the illumination compensa-

tion signiﬁcantly and can be extended, e.g., to least-

squares regression with two-dimensional second or-

der polynomials as shown below.

3.3 Least Squares Regression

We deﬁne the set P

x,y



, p



to contain a 5-by-

5 block of pixels within the image bounds that min-

imises the mean distance to the point (x, y). Then, we

can formulate the following minimisation problem

min

Aβ − b

with

A =







)







b =







f (p

, p

)

f (p

, p

)







This optimisation problem is solved by:

β =





−1

The intensity at (x, y) is approximated by

g(x, y) =



x y x

xy 1



· β.

Note that other regression approaches may also be

used. However, the complexity of a regression model,

i.e. the number of parameters to be estimated, should

be low, as illumination gradients are by deﬁnition

smooth functions. The choice of the neighbourhood

size is a trade-off between stability and runtime, but,

as our experiments show, 5-by-5 blocks are sufﬁcient

to remove almost all visible boundary artifacts. The

computational complexity of the regression method

is no crucial factor, as extrapolation is done only for

a low number of boundary pixels. So, other opera-

tions such as ﬁltering of the whole image dominate

the complexity of the illumination correction method.

3.4 Arbitrary Boundary Shapes

In some cases, it might be necessary to remove illumi-

nation gradients from images that contain more than

one texture. Here, the different textures should be seg-

mented and then individually corrected. In general,

these regions are non-rectangular, so the above meth-

ods have to be adapted for arbitrary shaped images.

Now, the input image f (x, y) is deﬁned only in certain

regions, i.e. the image contains valid intensities for a

set of pixels I ⊂ [0, m − 1] × [n − 1]. Then, (1) simply

needs to be modiﬁed to

(x, y) =



f (x, y) if (x, y) ∈ I

x,y

(x, y) otherwise.

(2)

In this more general case, it is not feasible to pick P

x,y

from a ﬁxed-size neighbourhood of a certain shape,

e.g. when I is very sparse or has a fractal-like bound-

ary. P

x,y

should rather contain a ﬁxed number of ad-

jacent pixels from within I.

ILLUMINATION CORRECTION FOR IMAGE STITCHING

3.5 The Final Algorithm

So far, we focused on the boundary extrapolation dur-

ing ﬁltering, but the aim is to correct illumination in-

homogeneities in texture images. In the overall algo-

rithm (see Alg. 1), extrapolation of boundary pixels is

used in steps (4) and (13).

Algorithm 1: Illumination correction algorithm.

input : Intensity image f (x, y), pyramid depth l

output: Corrected image f

(x, y)

1 G

← f ;

2 for i ← 0 to l do

3 Extend G

;

4 Extrapolate image G

; store results in G

;

5 Filter image, i.e. G

← h ∗ G

;

6 Crop image G

to original size;

7 Downsample, i.e. G

i+1

← (↓ 2)(G

);

8 end

9 G

← G

;

10 for i ← l down to 1 do

11 Upsample, i.e. G

i−1

← (↑ 2)G

;

12 Filter image, i.e. G

i−1

← h ∗ G

i−1

;

13 Extrapolate boundary; store results in G

i−1

;

14 Scale image, i.e. G

i−1

← 4 · G

i−1

;

15 end

16 Calculate mean intensity, i.e. f =

∑

f (x,y)

;

17 f

← f − G

+ f ;

In the downsampling loop, the image is ﬁrst ex-

tended by two rows and columns in each direction

and then the intensity values of these pixels are deter-

mined by extrapolation. After ﬁltering, the image is

cropped to the original size. In the upsampling loop,

the image is ﬁrst ﬁltered and then the intensity values

of the ﬁrst and last two rows and columns are recalcu-

lated from the inner image by extrapolation. Finally,

the low-frequency image is subtracted from the orig-

inal image and the mean intensity of the input image

is added to obtain the ﬁnal image with the proper in-

tensity level.

4 EXPERIMENTS

The performance of our method is demonstrated in a

series of experiments. We used gray-valued images

with intensity values ranging from 0 to 255. All op-

erations where done in double-precision arithmetic to

avoid discretisation artifacts.

We started with artiﬁcial images that contained no

texture but only smooth intensity gradients as they oc-

cur with natural vignetting (see Fig. 1). Perfect illumi-

nation correction would result in a completely homo-

geneous image. Obviously, the choice of the bound-

ary condition does not affect the centre of the image,

which shows a slight gradient even after correction.

At the image boundary the replicate condition is out-

performed by linear and polynomial extrapolation, the

latter yielding an image intensity range of less than 1

at the boundary. Thus, the correction is perfect at the

boundary for typical 8-bit images.

In a second experiment, we measured how bound-

ary artifacts affect the histogram of the intensity val-

ues. Therefore, we calculated the difference be-

tween the histograms of the image boundary (64 pix-

els wide) and the image centre (see Fig. 2). Here,

the replicate condition causes the corrected image to

be too dark at the boundary, i.e. the histogram of the

boundary pixels is shifted towards zero and the his-

togram difference has a maximum for small values.

With linear extrapolation, this effect is dramatically

reduced. Polynomial extrapolation gives only small

additional improvement.

In Fig. 3 some typical textures are depicted as they

occur in virtual material design. The images were ac-

quired with an industrial colour camera (1392 × 1040

pixels) and show clearly visible intensity falloffs to-

wards the image corners. We applied the above de-

scribed method for each colour channel individually

and compared it to the repetitive boundary condition.

After correction the intensity gradients are no longer

visible, however, other inhomogeneities and artifacts

are still obvious. These range from clearly visible

repetitive structure (see rows 2 and 3), to very subtle

blurring towards the image corners due to lens deﬁ-

ciencies.

5 CONCLUSIONS

We presented a novel method for removing illumina-

tion inhomogeneities from texture images based on

the Gaussian pyramid. With standard ﬁltering using

the replicate or circular boundary condition, the re-

sulting images will show artifacts at the image bor-

ders — mostly visible when stitching images together.

These artifacts can be avoided by different types of

boundary extrapolation. The framework is not lim-

ited to linear or polynomial extrapolation, however, it

seems unnecessary to use more complex functions.

The Gaussian pyramid provides a fast way to

model arbitrary illumination gradients. All calcula-

tions can be done in real-time — the proposed bound-

ary extrapolation techniques do not cause a signiﬁcant

performance drop due to their simplicity and the low

IMAGAPP 2011 - International Conference on Imaging Theory and Applications

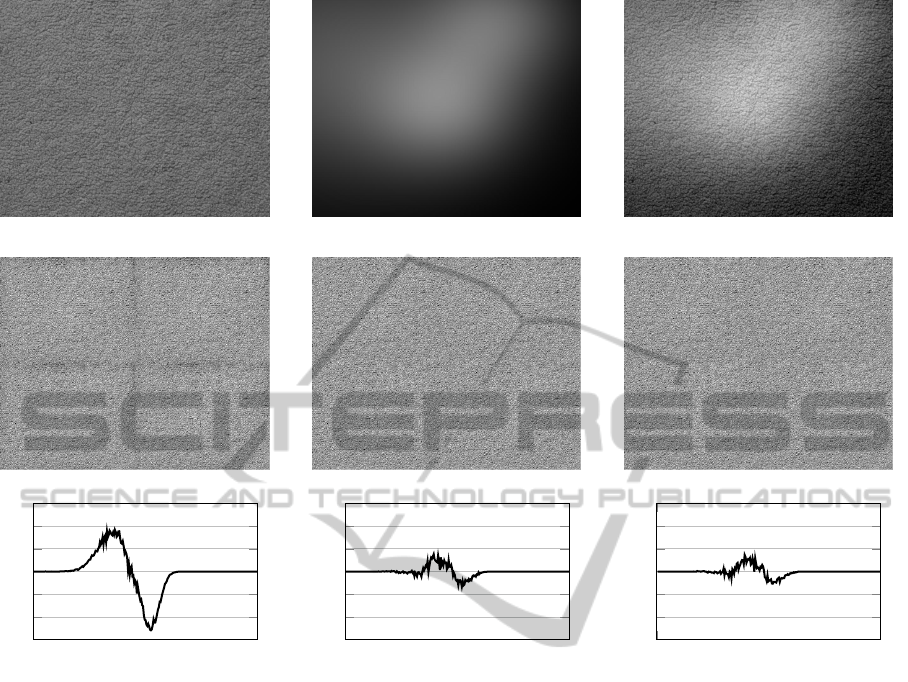
(a) Texture. (b) Gradient. (c) Combined.

255

−6

−4

−2

·10

−3

255

−6

−4

−2

·10

−3

255

−6

−4

−2

·10

−3

(d) Replicate condition. (e) Linear extrapolation. (f) Polynomial extrapolation.

Figure 2: Boundary artifacts in image mosaics. The top row shows a texture (a), a simulated illumination gradient (b)

and the combination of both (c). The middle row shows the correction results for three methods as 2-by-2 image mosaics.

The replicate condition (d) produces dark areas at the image transitions. With linear (e) or polynomial extrapolation (f) the

transitions are almost invisible. The difference between the histograms of centre and boundary pixel intensities (bottom)

veriﬁes this observation.

number of image boundary pixels. For colour images,

we apply the illumination correction for each channel

separately. On current PCs, we reach 20 frames per

second for SXGA colour images (1280 × 1024 px).

Finally, we shall discuss the role of illumination

correction in texture synthesis as it is used in virtual

material design. Besides intensity gradients, other im-

age acquisition artifacts, such as blurred image re-

gions, reﬂexions, or saturation may occur. All of

them will cause the results of na

ıve image stitching

to look repetitive and unrealistic, especially at the im-

age borders where the textures are non-continuous.

One solution would be to enhance the original image

and remove as many artifacts as possible. However, a

texture synthesis approach as proposed by Efros and

Freeman (Efros and Freeman, 2001) could avoid all

the above image acquisition artifacts by synthesising

larger textures from smaller blocks from the origi-

nal image. Each new block is chosen to optimise

an overlapping region and, ﬁnally, the blockiness of

the boundary is reduced by ﬁnding the minimum cost

path within the overlapping region. In this scenario,

illumination correction is again a fundamental prepro-

cessing step to avoid intensity gradients. Thus, our

method, in connection with the above texture synthe-

sis, results in natural looking textures of arbitrary size

and shape.

ILLUMINATION CORRECTION FOR IMAGE STITCHING

Figure 3: Real world colour textures. The performance of the illumination correction is shown for some real-world textured

materials (from top to bottom: paper towel, green linoleum, wood) in 3-by-3 image mosaics. Without illumination correction

(left column) vignetting is most obvious. The middle column shows image mosaics after correction with a replicate boundary

condition. Obviously, the correction using polynomial boundary extrapolation (right column) gives the best results.

REFERENCES

Adelson, E. H., Anderson, C. H., Bergen, J. R., Burt, P. J.,

and Ogden, J. M. (1984). Pyramid methods in image

processing. RCA Engineer, 29(6):33–41.

Adini, Y., Moses, Y., and Ullman, S. (1997). Face recog-

nition: the problem of compensating for changes in

illumination direction. IEEE TPAMI, 19:721–732.

Aggarwal, M., Hua, H., and Ahuja, N. (2001). On cosine-

fourth and vignetting effects in real lenses. In ICCV,

pages 472–479.

Efros, A. A. and Freeman, W. T. (2001). Image quilting for

texture synthesis and transfer. In SIGGRAPH, pages

341–346, New York, NY, USA. ACM.

Kim, S. J. and Pollefeys, M. (2008). Robust radiometric

calibration and vignetting correction. IEEE TPAMI,

30(4):562–576.

Levin, A., Zomet, A., Peleg, S., and Weiss, Y. (2004).

Seamless image stitching in the gradient domain. In

ECCV, pages 377–389. Springer-Verlag.

Levine, M. D., Gandhi, M. R., and Bhattacharyya, J. (2004).

Image normalization for illumination compensation in

facial images. unpublished.

Likar, B., Viergever, M. A., and Pernu

s, F. (2001). Ret-

rospective Correction of MR Intensity Inhomogeneity

by Information Minimization. IEEE Transactions on

Medical Imaging, 20(12):1398–1410.

Ogden, J. M., Adelson, E. H., Bergen, J. R., and Burt, P. J.

(1985). Pyramid-based computer graphics. RCA En-

gineer, pages 4–15.

Reyes-Aldasoro, C. (2009). Retrospective shading correc-

tion algorithm based on signal envelope estimation.

Electronics Letters, 45(9):454–456.

Zheng, Y., Lin, S., Kambhamettu, C., Yu, J., and Kang, S.

(2009). Single-image vignetting correction. PAMI,

31(12):2243–2256.

IMAGAPP 2011 - International Conference on Imaging Theory and Applications