
HUMAN ACTION RECOGNITION USING DIRECTION
AND MAGNITUDE MODELS OF MOTION
Yassine Benabbas, Samir Amir, Adel Lablack and Chabane Djeraba
LIFL UMR CNRS 8022, University of Lille1, TELECOM Lille1, Villeneuve d’Ascq, France
IRCICA, Parc de la Haute Borne, 56950 Villeneuve d’Ascq, France
Keywords:
Human action recognition, Motion analysis, Video understanding.
Abstract:
This paper proposes an approach that uses direction and magnitude models to perform human action recog-
nition from videos captured using monocular cameras. A mixture distribution is computed over the motion
orientations and magnitudes of optical flow vectors at each spatial location of the video sequence. This mix-
ture is estimated using an online k-means clustering algorithm. Thus, a sequence model which is composed
of a direction model and a magnitude model is created by circular and non-circular clustering. Human actions
are recognized via a metric based on the Bhattacharyya distance that compares the model of a query sequence
with the models created from the training sequences. The proposed approach is validated using two public
datasets in both indoor and outdoor environments with low and high resolution videos.
1 INTRODUCTION
Human action recognition and understanding is a
challenging topic in computer vision. It consists in the
automatic labeling of actions or activities performed
by a human being in a video sequence. Human ac-
tion recognition is important in a lot of domains. It
is widely used for video-surveillance to detect abnor-
mal events in public areas such as malls, metro sta-
tions or airports. In addition, disabled and aged peo-
ple can be more efficiently aided by monitoring their
daily actions using a system that recognizes and re-
ports them. Automatic labeling of actions is used to
improve human-computer interactions and video re-
trieval applications such as searching for fight scenes
in action movies or goals in soccer videos.
This paper presents an approach for human ac-
tion recognition from videos. The goal is to recog-
nize simple daily life actions (e.g. walking, answer-
ing a phone, etc.) in a video sequence. These ac-
tions consist of motion patterns performed by a sin-
gle person over a short period of time. Some ap-
proaches detect actions from still images, while other
approaches use as input stereoscopic videos or 3D
motion data (Ganesh and Bajcsy, 2008). In this work,
we use video sequences to detect actions by combin-
ing spatial and temporal information (Johansson et al.,
1994). We focus on monocular videos since they are
widespread and challenging.
The common approaches extract a set of image
features from the video sequence. Then, these fea-
tures are used classify the actions using training data.
The selection of the image representation and the
classification algorithms is influenced by the number
and type of actions, as well as the environment and
recording settings. In our approach we extract ma-
jor motion orientations and magnitudes at each loca-
tion of the scene using Gaussian mixtures and mix-
tures von Mises distributions. The von Mises distri-
bution was recently applied for trajectory shape anal-
ysis (Prati et al., 2008) and event detection in video
surveillance (Djeraba et al., 2010). These distribu-
tions form the direction and magnitude models. We
define then a distance metric between models to rec-
ognize the actions from training videos.
This paper is organized as follows: we highlight in
Section 2 the relevant works for human action recog-
nition. In Section 3, we describe our approach which
is composed of models creation and action recogni-
tion stages. We present and discuss the experimental
results of our approach in Section 4. Finally, we con-
clude and outline potential future work in Section 5.
2 RELATED WORK
Over the recent years, many techniques have been
proposed for human action recognition and under-
standing that are described in comprehensive surveys
277
Benabbas Y., Amir S., Lablack A. and Djeraba C..
HUMAN ACTION RECOGNITION USING DIRECTION AND MAGNITUDE MODELS OF MOTION.
DOI: 10.5220/0003323702770285
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2011), pages 277-285
ISBN: 978-989-8425-47-8
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

(Poppe, 2010; Turaga et al., 2008). We classify these
techniques according to the image representation and
the action classification algorithms that have been
used.
Image Representation. it describes how the fea-
tures extracted from the video sequences are repre-
sented. These features consist generally in optical
flow vectors (Ali and Shah, 2010), holistic features
(Kosmopoulos and Chatzis, 2010; Sun et al., 2009),
local spatio-temporal features such as the cuboids
features (Dollar et al., 2005) or the Hessian fea-
tures (Willems et al., 2008). A descriptor is then
constructed to represent the video sequence. It can
be done by training Ada-boost classifiers over low-
level features (Fathi and Mori, 2008), using motion-
sensitive responses to model motion contrasts (Es-
cobar et al., 2009), analyzing trajectories of moving
points (Messing et al., 2009) or spatio-temporal de-
scriptors such as HOG/HOF (Laptev et al., 2008),
HOG3D (Klser et al., 2008) or the extended SURF
(ESURF) (Willems et al., 2008).
Action Classification. it consists in finding the cor-
rect action associated to a query video. The clas-
sification can be performed using a classifier such
as SVM (Mauthner et al., 2009), Hidden Markov
Models (HMM) (Ivanov and Bobick, 2000; Kos-
mopoulos and Chatzis, 2010), Self Organizing Map
(SOM) (Huang and Wu, 2009) or Gaussian Pro-
cess (Wang et al., 2009b), a distance function such as
a transferable distance function (Yang et al., 2009) or
a discriminative model such as a Hidden Conditional
Random Field (HCRF) (Zhang and Gong, 2010) to
label the sequences as a whole.
Several datasets are available such as
KTH (Laptev and Lindeberg, 2004) and Activi-
ties of Daily Living (ADL) (Messing et al., 2009),
in order to train a classifier or to compare different
approaches.
Local spatio-temporal features have recently be-
come popular and have been shown successful for
human action recognition (Wang et al., 2009a).
Our models are inspired by the HOG/HOF fea-
tures (Laptev et al., 2008) that extract only the major
motion orientations/magnitudes and attributes them a
variance and a weight instead of coarse histograms
which are frequencies of the observations over inter-
vals. Our approach has the originality of using the di-
rection and magnitude models to represent the actions
without human body-part detection. Indeed, it relies
on the optical flow vectors as a feature to construct
the sequence model that is estimated and updated in
real time using an online algorithm. The model ex-
tracts major motion orientations and magnitudes at
each block of the scene. We choose this dense rep-
resentation for the models since this kind of sampling
generally outperforms other sampling methods (Wang
et al., 2009a). The actions are then recognized us-
ing a distance metric between the model associated
to the template sequences and the model of a query
sequence.
3 APPROACH DESCRIPTION
We propose in the following an approach that recog-
nizes actions performed by a single person. Figure 1
shows the main steps, divided into two major stages:
• Models Creation: quantifies the motion using the
optical flow vectors in order to estimate a direc-
tion model and a magnitude model over motion
orientations and magnitudes for the whole video
sequence.
• Action Recognition: recognizes the action as-
sociated to a query video by comparing its se-
quence model with the sequence models of tem-
plate videos using a distance metric.
Input video sequence
Optical flow computation
Direction model
Interest point detection
Circular clustering
Magnitude model
Non-circular clustering
Vector allocation to blocks
Model creation
(a)
Template models
Query model
Distance metric
Action decision
Action recognition
(b)
Figure 1: Approach steps. (a) Models creation stage, (b)
Action recognition stage.
3.1 Models Creation
In order to create the model of a video sequence, we
start by extracting a set of interest points from each in-
put frame. We consider Shi and Tomasi feature detec-
tor (Shi and Tomasi, 1994) which finds corners with
high eigenvalues in the frame. We also consider that,
in our targeted video scenes, camera positions and
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
278

lighting conditions allow a large number of interest
points to be captured and tracked easily.
Once we define the set of points of interest, we
track them over the next frames using optical flow
vectors. We have used Bouguet’s (Bouguet, 2000) im-
plementation of the KLT tracker (Lucas and Kanade,
1981) which is good at handling features near the
image border in addition to its computational effi-
ciency. The result of the operation of matching fea-
tures between frames is a set of four-dimensional vec-
tors V = {V
1
...V
N
|V
i
= (X
i
,Y
i
,A
i
,M
i
)}, where:
• X
i
and Y
i
are the image location coordinates of the
feature i,
• A
i
: is the motion direction of the feature i.
• M
i
: is the motion magnitude of the feature i; it
corresponds to the distance between the position
of feature i in the frame f and its corresponding
position in the frame f + 1.
This step also allows the removal of static features
that move less than a minimum magnitude. We re-
move also noise features whose magnitudes exceed
the threshold. In our experiments, we set the mini-
mum motion magnitude to 1 pixel per frame and the
maximum to 20 pixels per frame.
The next step consists in dividing the scene into
a grid of W × H blocks. Then, each vector is allo-
cated to its corresponding block depending on its ori-
gin. The size of the block affects the precision of the
system and will be discussed in Section 4.3.
Then, for each block, we apply a circular cluster-
ing algorithm to the orientations of the optical flow.
The set of W × H estimated circular distributions is
called the direction model. Figure 2 illustrates the
construction of the direction model associated to an
’answerPhone’ action.
In this work, we cluster circular data using a mix-
ture of von Mises distribution. Thus, the probability
of an orientation θ with respect to the block B
x,y
is
defined by:
p
x,y
(θ) =
K
∑
i=1
ψ
i
x,y
·V
θ;φ
i
x,y
,γ
i
x,y
where K is the number of distributions and repre-
sents the maximum number of major orientations to
consider (we choose empirically K = 4 which corre-
sponds to the 4 cardinal directions). ψ
i
x,y
, φ
i
x,y
, γ
i
x,y
denote respectively the weight, mean angle and dis-
persion of the i
th
distribution for the block B
x,y
. The
von Mises distribution V (θ; φ,γ) with mean orienta-
tion φ and dispersion parameter γ, over the angle θ,
has the following probability density function:
(a) (b)
(c) (d)
Figure 2: Direction model of an ’answerPhone’ action. (a)
current frame, (b) Optical flow vectors, (c) Direction model
of the video sequence, (d) Magnitude model of the video
sequence.
V (θ;φ,γ) =
1
2πI
0
(γ)
exp[γcos(θ − φ)]
where I
0
(γ) is the modified Bessel function of the first
kind and order 0 defined by the following equation:
I
0
(γ) =
∞
∑
r=0
1
r!
2
1
2
γ
2r
By analogy, we cluster the magnitudes of the op-
tical flow vectors for each block using Gaussian mix-
tures. The set of estimated Gaussian mixtures con-
stitutes the magnitude model as illustrated in Figure
2(d). Thus, the probability of a magnitude v with re-
spect to the block B
x,y
is defined by:
p
x,y
(v) =
J
∑
i=1
ω
i
x,y
G(v;µ
i
x,y
,σ
2
i
x,y
)
where ω
i
x,y
,µ
i
x,y
,σ
2
i
x,y
are respectively the weight,
mean and variance of the i
th
Gaussian distribution.
HUMAN ACTION RECOGNITION USING DIRECTION AND MAGNITUDE MODELS OF MOTION
279

For each frame, we update the Gaussian mixture
parameters using a K-means approximation algorithm
described in (Kaewtrakulpong and Bowden, 2001).
We use k-means also to update the parameters of the
mixture of von Mises distributions by adapting the al-
gorithm in order to deal with circular data and con-
sidering the inverse of the variance as the dispersion
parameter; γ = 1/σ
2
. The circular clustering algo-
rithm is given below and works as follows: It gets
as input a data point x which is an orientation in our
case. Then, this orientation is matched against the
first distribution in the mixture. If no distribution sat-
isfies the matching condition, then the last distribution
is replaced by a distribution with a mean equal to the
new orientation. After that, the parameters of all the
distributions in the mixture are updated. Finally, the
distribution are sorted according to a fitness. This last
action allows to define the order of the distributions
for the next matching.
Figure 3 shows the detected clusters in block using
our algorithm. We remind that our circular cluster-
ing algorithm did not process the hole data illustrated
in Figure 3(a) in a single run. In fact, the algorithm
is run at each frame and clusters are updated as data
is added to the block. Thus, the temporal dimension
impacts the final results. This explains the different
clusters even if the whole data may be assimilated to
a single cluster when we do not consider the temporal
dimension.
(a) (b)
Figure 3: Representation of the estimated clusters using our
circular clustering algorithm. (a) accumulated raw data, (b)
estimated clusters.
In the following, we note the model of the se-
quence s by Sm(s) = (Dm(s), Mm(s)), where Dm(s)
and Mm(s) are respectively the direction model and
the magnitude model associated to the sequence s.
Figure 7 shows the direction and magnitude models
of some video sequences from the KTH dataset.
3.2 Action Recognition
Once the model of a video sequence has been com-
puted, we detect the action that corresponds to this
Algorithm 1: Online-mVM.
1: input a data point x on R
2: a mixture of K vM distributions
3: return an updated clustering over a mixture of K
von Mises distributions
4: initialize learning rate α = 1/400
5: initialize matching threshold β = 2.5
6: c ← 0
7: for i = 1 to K do
8: {Getting the first match for the input value}
9: if c = 0 and x − θ
i
≤ β
2
/γ
i
then
10: c ← i
11: end if
12: end for
13: if c 6= 0 then
14: {a match is found, update the parameters}
15: for i = 1 to K do
16: ψ
i
← ψ
i
(1 − α)
17: end for
18: ψ
c
← ψ
c
+ α
19: ρ ← αψ
c
(x − θ
c
)
20: θ
c
← θ
c
+ ρ
21: γ
c
← (γ
−1
c
+ ρ
2
− γ
−1
c
)
−1
22: n
c
← n
c
+ 1
23: else
24: {no match found, discard the last distribution}
25: n
k
← 1
26: θ
k
← x
27: γ
k
← γ
0
28: for i = 1 to K do
29: ψ
i
←
n
i
∑
k
j=1
n
j
30: end for
31: end if
32: sort distributions by weight × dispersion
’query’ video by comparing its model with the mod-
els of the template sequences using a distance metric.
The action associated to the model that has the short-
est distance with the model of the query sequence is
then selected.
Let T = {t
1
,t
2
,...,t
n
} be a set of n tem-
plate sequences and their respective models are
{Sm(t
1
),Sm(t
2
),...,Sm(t
n
)}. Given a query sequence
q with its model Sm(q), the distance between Sm(q)
and a template sequence model Sm(t
l
) is defined by:
D(Sm(q),Sm(t
l
)) =
Norm(A
Dm(q),Dm(t
l
)
) + Norm(B
Mm(q),Mm(t
l
)
)
where Norm corresponds to the L2-Norm. The W ×H
matrices A
Dm(q),Dm(t
l
)
and B
Mm(q),Mm(t
l
)
contain the
distances between each element of the two direction
models Dm(q) and Dm(t
l
) and the two magnitude
models Mm(q) and Mm(t
l
) respectively. Each ele-
ment A
M,M
0
(x,y) is defined by the following formula:
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
280

A
M,M
0
(x,y) =
K
∑
i=1
ψ
i
x,y
ψ
0
i
x,y
Dist
d
(V
i
x,y
,V
0
i
x,y
)
where ψ
i
x,y
(resp. ψ
0
i
x,y
) and V
i
x,y
(resp. V
0
i
x,y
) are the
i
th
weight and i
th
von Mises distribution associated
to the direction model M (resp. M
0
) at the block
B
x,y
. Dist
d
(V,V
0
) is the Bhattacharyya distance be-
tween two von Mises distributions V and V
0
defined
by the following equation:
Dist
d
(V,V
0
) =
s
1 −
Z
+∞
−∞
p
V (θ)V
0
(θ)dθ
where 0 ≤ Dist
d
(V,V
0
) ≤ 1. This equation can be
computed using the closed form expression:
Dist
d
(V,V
0
) =
v
u
u
t
1 −
s
1
I
0
(γ)I
0
(γ
0
)
I
0
p
γ
2
+ γ
02
+ 2γγ
0
cos(φ − φ
0
)
2
!
where φ (resp. φ
0
) and γ (resp. γ
0
) are respectively
the mean angle and the dispersion parameter of the
distribution V (resp. V
0
).
By analogy, we define each element B
N,N
0
(x,y) by
the following equation:
B
N,N
0
(x,y) =
K
∑
i=1
ω
i
x,y
ω
0
i
x,y
Dist
m
(G
i
x,y
,G
0
i
x,y
)
where ω
i
x,y
(resp. ω
0
i
x,y
) and G
i
x,y
(resp. G
0
i
x,y
) are
the i
th
weight and Gaussian distribution associated to
the magnitude model N (resp. N
0
) at the block B
x,y
.
Dist
m
(G,G
0
) is the Bhattacharyya distance between
two Gaussian distributions G and G
0
defined by the
following closed form expression:
Dist
m
(G,G
0
) =
(µ − µ
0
)
2
4(σ
2
+ σ
0
2
)
+
1
2
ln
σ
2
+ σ
0
2
2σσ
0
!
where µ (resp. µ
0
) and σ
2
(resp. σ
0
2
) are re-
spectively the mean and the variance of the distri-
bution G (resp. G
0
). We note that this step al-
lows parallelization out of the box since computing
D(Sm(q),Sm(t
i
)) for any i < n does not require to
compute D(Sm(q),Sm(t
j
)); j < n, j 6= i.
We believe that our method can perform in real
time because the models creation step is performed
online and the action recognition step can be paral-
lelized. However, our current implementation does
yet not parallelize the processing.
4 EXPERIMENTS AND RESULTS
We demonstrate the performance of our approach
using two standard datasets containing a variety of
daylife actions. In addition to the confusion matrices,
we also report the effect of different number of action
classes and different block sizes to the efficiency and
effectiveness of the system.
4.1 Action Recognition Performance
KTH dataset (Laptev and Lindeberg, 2004): is a
dataset that contains low resolution videos (gray-scale
images with a resolution of 160 × 120 pixels) of 6 ac-
tions performed several times by 25 different subjects.
This dataset is challenging because the sequences are
recorded in different indoor and outdoor scenarios
with scale variations and different clothes. We divide
the dataset as suggested by Schuldt et al. (Schuldt
et al., 2004) into two sets, a training set (16 people)
and a test set (9 people). We include ’person01’ to
’person16’ in the training set and ’person17’ to ’per-
son25’ in the validation set. We use a block size of
5 × 5 pixels.
0
1
2
3
4
5
(a)
0-boxing
0.56 0.07 0.22 0.04 0.07 0.04
1-handclapping
0.04 0.93 0.04 0.00 0.00 0.00
2-handwaving
0.00 0.00 0.85 0.00 0.07 0.07
3-walking
0.07 0.00 0.00 0.79 0.07 0.07
4-running
0.07 0.00 0.00 0.48 0.22 0.22
5-jogging
0.07 0.00 0.00 0.59 0.19 0.15
boxing
handclapping
handwaving
walking
running
jogging
(b)
Figure 4: Results on KTH dataset. (a) Action samples, (b)
Confusion matrix using a block size of 5 × 5.
Action samples and the confusion matrix are re-
ported in Figure 4. Our approach is able to achieve
satisfying results on the first three actions of this
dataset where the human is motionless. However, our
system considers the ’running’ and ’jogging’ actions
as ’walking’; this is due to the fact that these actions
differ slightly in speed and stride length and have sim-
ilar orientations.
Activities of Daily Living (ADL) Dataset (Messing
et al., 2009): is a dataset that contains high resolu-
tion videos (1280 ×720 pixels) of 10 daily life actions
(such as peelBanana, useSilverware, answerPhone)
performed by 5 different subjects. We follow the
leave-one-out experimentation protocol in our evalu-
ation. It is performed by considering a sequence as
a query sequence, and all the remaining ones as tem-
plate sequences for the recognition of an action. This
HUMAN ACTION RECOGNITION USING DIRECTION AND MAGNITUDE MODELS OF MOTION
281

procedure is performed for all sequences and the re-
sults are averaged for each action category.
In Figure 5, we present the confusion matrix ob-
tained with our approach on this dataset. The ap-
proach achieved an average accuracy of 0.84 with a
block size of 5×5 pixels. It is a very satisfying perfor-
mance, however, the peelBanana action is confused
with the actions eatSack and useSilverware.
(a)
answerPhone
0.93 0.00 0.07 0.00 0.00 0.00 0.00 0.00 0.00 0.00
chopBanana
0.00 0.93 0.00 0.00 0.07 0.00 0.00 0.00 0.00 0.00
dialPhone
0.13 0.00 0.87 0.00 0.00 0.00 0.00 0.00 0.00 0.00
drinkWater
0.00 0.00 0.00 1.00 0.00 0.00 0.00 0.00 0.00 0.00
eatBanana
0.00 0.00 0.00 0.00 0.73 0.00 0.00 0.20 0.07 0.00
eatSnack
0.00 0.00 0.00 0.00 0.00 0.80 0.00 0.20 0.00 0.00
lookupInPhonebook
0.00 0.00 0.00 0.00 0.00 0.00 1.00 0.00 0.00 0.00
peelBanana
0.00 0.00 0.06 0.00 0.07 0.13 0.07 0.47 0.20 0.00
useSilverware
0.00 0.00 0.00 0.00 0.07 0.00 0.00 0.20 0.73 0.00
writeOnWhiteboard
0.00 0.00 0.07 0.00 0.00 0.00 0.00 0.00 0.00 0.93
answerPhone
chopBanana
dialPhone
drinkWater
eatBanana
eatSnack
lookupInPhonebook
peelBanana
useSilverware
writeOnWhiteboard
(b)
Figure 5: Results on ADL dataset. (a) Action samples, (b)
Confusion matrix using a block size of 5 × 5.
4.2 Comparative Study
We compare our approach with other systems us-
ing KTH and Activities of Daily Living datasets and
present their precision in Table 1. It shows that the
approaches which are based on local spatio-temporal
features (Dollar et al., 2005; Laptev et al., 2008) and
velocity histories (Messing et al., 2009) outperform
our system on the KTH dataset. The latter uses the
velocities of tracked key-points as low-level features.
However, our system gets a better precision on the
Activities of Daily Living (ADL) dataset because it
combines both motion magnitude and orientation in-
formation.
Compared to the HOG/HOF features (Laptev
et al., 2008), our scene model learns major motion
orientations/magnitudes and does not consider noisy
motion. In addition, each mixture distribution re-
Table 1: Comparison of classifying precision on 2 different
datasets.
Method ADL KTH
Our proposed approach 0.84 0.58
Velocity histories (Messing
et al., 2009)
0.63 0.74
Space-time interest Points
(Laptev et al., 2008)
0.59 0.80
Spatio-temporal Cuboids (Dol-
lar et al., 2005)
0.36 0.66
turns exact mean orientations with their variances
and weight. While the HOG/HOF features compute
coarse histograms of oriented gradients (HOG) and
optical flow (HOF). Moreover, a histogram computes
frequencies over intervals, which is less precise than
our method since the latter computes mean values in
the scene model. Our approach has better results on
the high resolution ADL dataset since the motion in-
formation is more precise. However, our approach
suffered from the the lack of precision and the fre-
quent noise in low resolution videos.
Some other approaches achieve good results on
the KTH dataset but we cannot compare to them be-
cause of their different setup. They have either used
more training data or subdivided the problem into
simpler tasks.
4.3 Performance on Action Powerset
We study the influence of the block size and the num-
ber of action classes using the KTH dataset. Thus, we
have repeated the experimentation on each element of
the powerset of the KTH set of actions: hand-waving,
boxing, hand-clapping, walking, running and jogging,
which we note A = {0,1,2,3,4,5} respectively (0 for
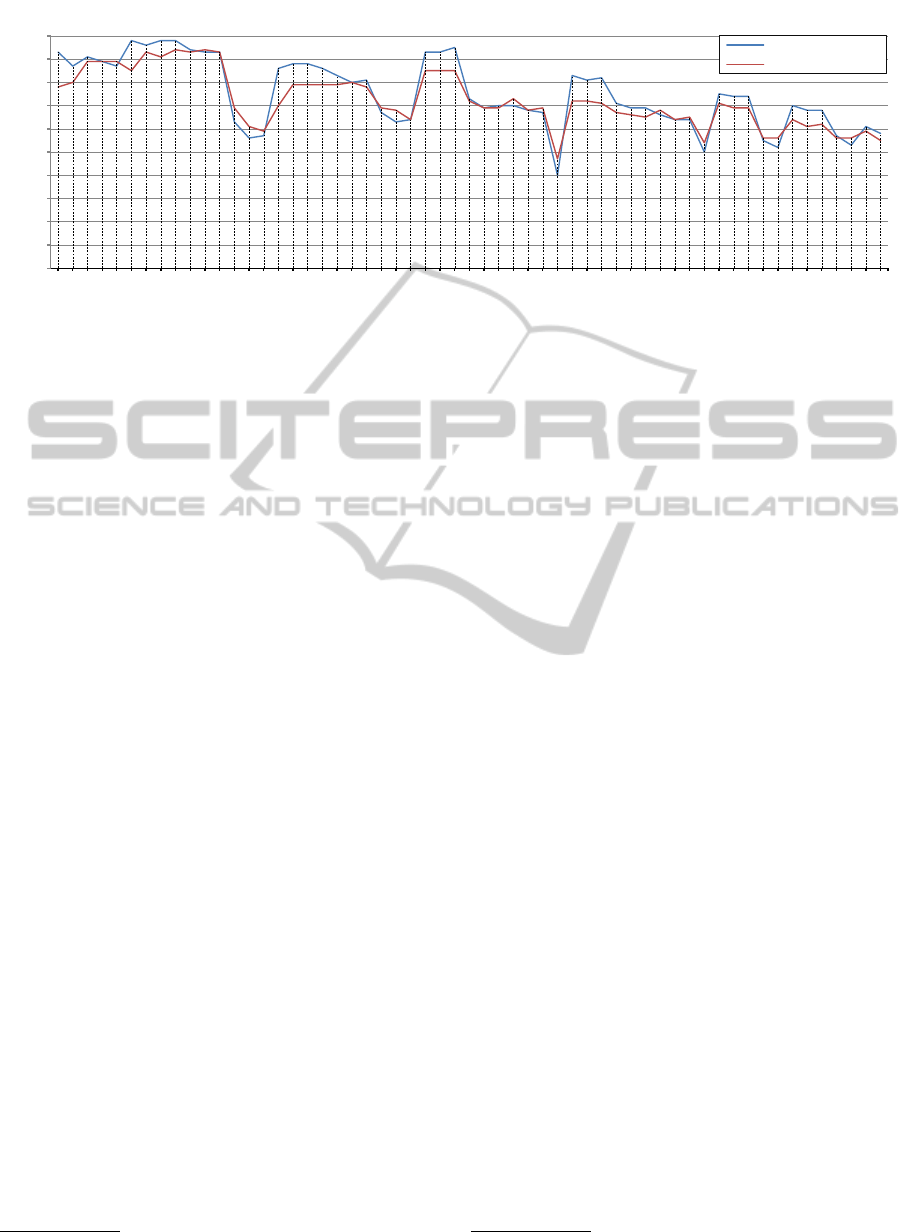
hand-waving, 1 for boxing,...etc). The graphs in Fig-
ure 6 show the precision of our system for each subset
of A. The blue graph is obtained using a block size of
5 × 5 pixels while the red graph is obtained using a
block size of 10 × 10 pixels.
The precision of the combination 012345 using a
block size of 5 × 5 pixels is 0.58. It corresponds to
the total precision of our system as reported in sec-
tion 4. The lowest precision rate (∼ 40%) is reached
with the combination 345 which corresponds to the
actions jogging, running and walking. It highlights
the difficulty to distinguish between the speeds of re-
lated actions in low resolution videos.
Our experiments show also that increasing the
block size reduces the precision of the action recog-
nition system but decreases exponentially the pro-
cessing time. In addition, increasing the number of
template sequences increases the processing. How-
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
282
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
01
02
03
04
05
12
13
14
15
23
24
25
34
35
45
012
013
014
015
023
024
025
034
035
045
123
124
125
134
135
145
234
235
245
345
0123
0124
0125
0134
0135
0145
0234
0235
0245
0345
1234
1235
1245
1345
2345
01234
01235
01245
01345
02345
12345
012345
Precision
Actions combinations
block size = 5x5
block size = 10x10
boxing : 0 , handclapping : 1 , handwaving : 2 , walking : 3 , running : 4 , jogging : 5
Figure 6: Influence of the block size and actions combinations on the precision.
ever this does not necessarily imply increasing perfor-
mance, because we reached 0.51 precision rate on the
KTH dataset using the leave-one-out experimentation
protocol as in the Activities of Daily Living (ADL)
dataset. We also note that some action combinations
are better detected using a block size of 10 × 10, this
a lead to improve our system by using dynamic bloc
sizes depending on the actions.
5 CONCLUSIONS
We have presented an effective action recognition sys-
tem that relies on direction and magnitude models.
We have extracted optical flow vectors from video se-
quences in order to learn statistical models over mo-
tion orientations and magnitudes. The result is a se-
quence model that estimates major orientations and
magnitudes in each spatial location of the scene. We
have used a distance metric to recognize an action
by comparing the model of a query sequence with
the models of template sequences. Relying on mo-
tion orientations and magnitudes, our approach has
shown promising results compared to other state-of-
the art approaches in particular using high resolution
videos. Our future work will focus on two directions:
improving the flexibility of the classifier with respect
to adding or removing action classes, and performing
action detection for online applications.
ACKNOWLEDGEMENTS
This work has been supported by the Multi-modal In-
terfaces for Disabled and Ageing Society
1
(MIDAS)
1
http://www.midas-project.com/
ITEA 2-07008 European project and the French ANR
project Comportements Anormaux Analyse Detec-
tion Alerte
2
(CAnADA).
REFERENCES
Ali, S. and Shah, M. (2010). Human action recognition in
videos using kinematic features and multipleinstance
learning. IEEE Transactions on Pattern Analysis and
Machine Intelligence (TPAMI), 32(2):288–303.
Bouguet, J.-Y. (2000). Pyramidal implementation of the
lucas kanade feature tracker description of the algo-
rithm. Intel Corporation Microprocessor Research
Labs.
Djeraba, C., Lablack, A., and Benabbas, Y. (2010). Multi-
Modal User Interactions in Controlled Environments.
Springer-Verlag.
Dollar, P., Rabaud, V., Cottrell, G., and Belongie, S. (2005).
Behavior recognition via sparse spatio-temporal fea-
tures. In 2nd International Workshop on Visual
Surveillance and Performance Evaluation of Tracking
and Surveillance (PETS), pages 65–72.
Escobar, M.-J., Masson, G. S., Vieville, T., and Kornprobst,
P. (2009). Action recognition using a bio-inspired
feedforward spiking network. International Journal
of Computer Vision (IJCV), 82(3):284–301.
Fathi, A. and Mori, G. (2008). Action recognition by learn-
ing mid-level motion features. In International Con-
ference on Computer Vision and Pattern Recognition
(CVPR).
Ganesh, S. and Bajcsy, R. (2008). Recognition of hu-
man actions using an optimal control based motor
model. In Workshop on Applications of Computer Vi-
sion (WACV).
Huang, W. and Wu, J. (2009). Human action recognition us-
ing recursive self organizing map and longest common
2
http://liris.cnrs.fr/equipes/?id=38&onglet=conv
HUMAN ACTION RECOGNITION USING DIRECTION AND MAGNITUDE MODELS OF MOTION
283

subsequence matching. In Workshop on Applications
of Computer Vision (WACV).
Ivanov, Y. and Bobick, A. (2000). Recognition of visual
activities and interactions by stochastic parsing. Pat-
tern Analysis and Machine Intelligence, IEEE Trans-
actions on, 22(8):852 –872.
Johansson, G., Bergstrm, S. S., Epstein, W., and Jansson,
G. (1994). Perceiving Events and Objects. Lawrence
Erlbaum Associates.
Kaewtrakulpong, P. and Bowden, R. (2001). An im-
proved adaptive background mixture model for real-
time tracking with shadow detection. In 2nd European
Workshop on Advanced Video Based Surveillance Sys-
tems.
Klser, A., Marszaek, M., and Schmid, C. (2008). A spatio-
temporal descriptor based on 3d-gradients. In British
Machine Vision Conference (BMVC).
Kosmopoulos, D. and Chatzis, S. (2010). Robust visual
behavior recognition, a framework based on holistic
representations and multicamera information fusion.
IEEE Signal Processing Magazine, 27(5):34 –45.
Laptev, I. and Lindeberg, T. (2004). Velocity adaptation of
space-time interest points. In International Confer-
ence on Pattern Recognition (ICPR), pages 52–56.
Laptev, I., Marszałek, M., Schmid, C., and Rozenfeld,
B. (2008). Learning realistic human actions from
movies. In International Conference on Computer Vi-
sion and Pattern Recognition (CVPR).
Lucas, B. and Kanade, T. (1981). An iterative image regis-
tration technique with an application to stereo vision.
In International Joint Conference on Artificial Intelli-
gence (IJCAI), pages 674–679.
Mauthner, T., Roth, P. M., and Bischof, H. (2009). Instant
action recognition. In 16th Scandinavian Conference
on Image Analysis (SCIA).
Messing, R., Pal, C., and Kautz, H. (2009). Activity
recognition using the velocity histories of tracked key-
points. In International Conference on Computer Vi-
sion (ICCV).
Poppe, R. (2010). A survey on vision-based human ac-
tion recognition. Image and Vision Computing (IVC),
28(6):976 – 990.
Prati, A., Calderara, S., and Cucchiara, R. (2008). Using
circular statistics for trajectory shape analysis. In In-
ternational Conference on Computer Vision and Pat-
tern Recognition (CVPR), pages 1 –8.
Schuldt, C., Laptev, I., and Caputo, B. (2004). Recognizing
human actions: A local svm approach. In Interna-
tional Conference on Pattern Recognition (ICPR).
Shi, J. and Tomasi, C. (1994). Good features to track. In
Internatioal Conference on Computer Vision and Pat-
tern Recognition (CVPR), pages 593–600.
Sun, X., Chen, M., and Hauptmann, A. (2009). Ac-
tion recognition via local descriptors and holistic fea-
tures. In IEEE Computer Society Conference on
Computer Vision and Pattern Recognition Workshops,
2009 (CVPR Workshops), pages 58 –65.
Turaga, P., Chellappa, R., Subrahmanian, V. S., and Udrea,
O. (2008). Machine recognition of human activities:
A survey. IEEE Transactions on Circuits and Systems
for Video Technology, 18(11):1473–1488.
Wang, H., Ullah, M. M., Kl
¨
aser, A., Laptev, I., and Schmid,
C. (2009a). Evaluation of local spatio-temporal fea-
tures for action recognition. In British Machine Vision
Conference.
Wang, L., Zhou, H., Low, S.-C., and Leckie, C. (2009b).
Action recognition via multi-feature fusion and gaus-
sian process classification. In Workshop on Applica-
tions of Computer Vision (WACV), pages 1 –6.
Willems, G., Tuytelaars, T., , and Gool, L. V. (2008). An ef-
ficient dense and scale-invariant spatio-temporal inter-
est point detector. In European Conference on Com-
puter Vision (ECCV).
Yang, W., Wang, Y., and Mori, G. (2009). Efficient human
action detection using a transferable distance function.
In Asian Conference on Computer Vision (ACCV).
Zhang, J. and Gong, S. (2010). Action categorization with
modified hidden conditional random field. Pattern
Recognition (PR), 43(1):197–203.
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
284
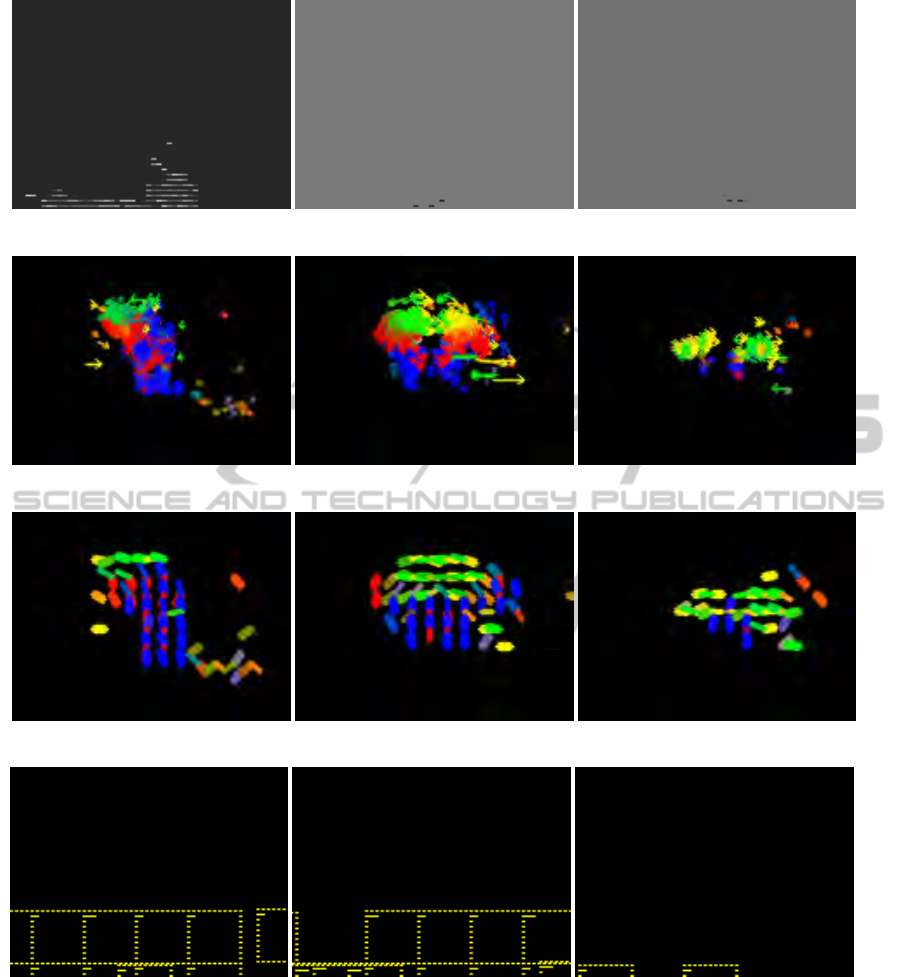
(a) Sample frames
(b) Optical flow vectors
(c) Direction model
(d) Magnitude model
Figure 7: Sample frames with associated direction models and magnitude models.
HUMAN ACTION RECOGNITION USING DIRECTION AND MAGNITUDE MODELS OF MOTION
285
