EFFICIENT UNIFORM GRIDS FOR COLLISION HANDLING

IN MEDICAL SIMULATORS

Marc Gissler, Markus Ihmsen and Matthias Teschner

Computer Science Department, University of Freiburg, Freiburg, Germany

Keywords:

Spatial data structures, Collision detection, Collision response, Cell indexing, Spatial hashing, Cuckoo hash-

ing.

Abstract:

We investigate spatial acceleration structures within collision handling in scenarios with ”worst-case” spatial

layout. These are scenarios where lots of collisions and interactions persist over large time intervals. We

focus on acceleration structures based on uniform grids and assess their efﬁciency in construction, update and

query. Z-curves as a technique for the mapping of spatial locality to uniform grids are analyzed to improve the

cache-hit rate. The ﬁndings are applied to a deformable collision framework. Experiments are performed on

scenarios that are typical for medical simulators. They often exhibit the ”worst case” spatial layout mentioned

above.

1 INTRODUCTION

Collision handling and the computation of the dynam-

ics are commonly the two main tasks in physically-

based animations. While the computation time for

the dynamics is generally constant, it can signiﬁcantly

vary for the collision handling dependent on the spa-

tial conﬁguration of the environment. This is due to

the fact that spatial acceleration structures are em-

ployed. They reduce the search space for collisions

to pairs of primitives that are in the same spatial parti-

tion. On the other hand, the collision handling can

get rather expensive in application scenarios where

lots of collisions persist over large time intervals, e. g.

the mesh representations of organs in medical sim-

ulations are in constant interaction with each other.

Various solutions exist to reduce the computational

work in such cases. One is to keep the candidates

for intersection tests to a minimum by optimizing

the spatial partitioning or by improved culling (Tang

et al., 2008). On the other hand, the construction, up-

date and query performance of the spatial accelera-

tion structures could be improved. Time-critical col-

lision handling is a research topic that is concerned

with time constraints at the expense of accuracy(Hub-

bard, 1996). With respect to dynamics simulations,

an approximate collision handling might still yield

visually plausible results (O’Sullivan and Dingliana,

2001; Gissler et al., 2009). We focus on the research

areas of efﬁcient data structures, parallel algorithms

and approximate techniques.

Our Contribution: We investigate parallel data

structures based on uniform grids in terms of efﬁcient

construction, update and query. We discuss various

representations of uniform grids and their particular

properties. We describe Z-curves as a technique for

the mapping of spatial locality to uniform grids and

analyze their impact on the cache-hit rate. Regarding

the index sorting approach, we analyze various sort-

ing algorithms. The ﬁndings are applied in the colli-

sion handling step, i. e. in both collision detection and

collision response, of a deformable collision frame-

work. Experiments are performed on scenarios from

medical simulators. They are speciﬁcally challenging

because of their spatial layout, i. e., the simulated ob-

jects are in constant interaction with each other.

2 RELATED WORK

The problem of collision detection has been exten-

sively studied in the areas of computer graphics, sim-

ulation, computational geometry and robotics. For

excellent surveys, we refer the reader to (Lin and

Manocha, 2003; Ericson, 2004; Teschner et al., 2005;

Fares and Hammam, 2005; Kockara et al., 2007). A

comprehensivesurveyon the underlying search meth-

Gissler M., Ihmsen M. and Teschner M..

EFFICIENT UNIFORM GRIDS FOR COLLISION HANDLING IN MEDICAL SIMULATORS.

DOI: 10.5220/0003324300790084

In Proceedings of the International Conference on Computer Graphics Theory and Applications (GRAPP-2011), pages 79-84

ISBN: 978-989-8425-45-4

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

ods and data structures can be found in (Bentley and

Friedman, 1979). We focus on the discussion of ap-

proaches based on uniform grids.

Uniform grids discretize k-dimensional spaces

into cells. (Levinthal, 1966) ﬁrst applied grids to

three-dimensional range queries. Recent research on

uniform grids considers the memory requirements

and parallelization techniques. (Lagae and Dutr´e,

2008) propose a compact representation of uniform

grids and discuss its application in GPU-based ray

tracing. In (Kalojanov and Slusallek, 2009), efﬁcient

parallel grid construction is considered in the context

of ray tracing. They propose an algorithm for which

the performance does not depend on the primitive dis-

tribution, because the constructionproblem is reduced

to sorting pairs of primitives and cell indices. In (Ra-

bin, 1976), hash maps are proposed for a compact rep-

resentation of a three-dimensional grid. Many hash-

ing techniques have been proposed such as perfect

hashing (Fredman et al., 1984), multiple-choice per-

fect hashing (Pagh and Rodler, 2004) or combinations

of both (Alcantara et al., 2009). In (Teschner. et al.,

2003), an optimized spatial hashing technique for the

collision detection of deformable objects is proposed.

Space-ﬁlling curves (SFC) feature the ability to pre-

serve spatial locality of an initial domain. In (Griebel

and Zumbusch, 1998), SFCs as a method of order-

ing sparse rectangular grids were introduced. An efﬁ-

cient computation of the Lebesgue space ﬁlling curve

is proposed in (Pascucci and Frank, 2001). We pro-

pose to employ SFCs for the computation of the cell

index to increase the efﬁciency of the discussed colli-

sion handling approaches.

3 SPATIAL DATA STRUCTURES

3.1 Uniform Grid

A uniform grid partitions the simulation domain into

regular grid cells of size d. If the domain is bounded

by an axis-aligned bounding box (AABB) with e

min

and e

max

being its minimum and maximum extent, the

grid cells can be stored in an array of size s

∗ s

and s = (s

) =



max

− e

min

)



. The cell index

c of a point with position p = (x,y,z) can be computed

as:

c = i+ j∗ s

+ k∗ s

∗ s

with

(i, j,k) =



x−e

min



y−e

min



z−e

min



. Each

cell has to store references to all the primitives that

overlap the cell. Usually, the references are stored in

either linked lists or dynamic arrays. Using dynamic

arrays requires more memory, but improves the local-

ity of the references.

3.2 Compact Grid

A compact grid both requires low memory and keeps

the locality of the references (Lagae and Dutr´e, 2008).

It consists of two static arrays. The ﬁrst is an indirec-

tion array L that stores references to primitives. The

second array C contains the indexed cells of the grid.

Each grid cell stores a pointer to the beginning of an

interval within the array L. The end of the interval

is implicitly given by the pointer in the adjacent cell

within C. Primitives that are referenced within this

interval are contained in the respective cell. Thus, the

referencesin L can be seen as sorted according to their

cell index.

Parallel Construction: We employ the algorithm

proposed in (Kalojanov and Slusallek, 2009) to con-

struct the compact grid. Its independent of the primi-

tive distribution, because the construction problem is

reduced to sorting. The algorithm ﬁrst iterates over all

primitives and counts how many cells the primitives

intersect to reserve space for L. The entries of L are

computed in a second iteration. An entry consists of

a cell index and a pointer to the respective primitive.

L is then sorted according to the cell index. Then, all

primitives that lie within the same cell are contiguous

in L. In the ﬁnal step, parallel reduction is performed

to compute the offsets stored in C . The complexity

and performance of the compact grid construction are

deﬁned by the employed sorting algorithm.

Parallel Query: The query is performed by looping

in parallel over the corresponding primitives, e. g. the

tetrahedrons, per model. The cell index is computed

and the primitives, e. g. the points, that are assigned

to the same cell are tested for intersection by lookups

in L via the offset stored in C.

3.3 Spatial Hashing

In contrast to basic uniform grids or compact grids,

spatial hashing can be employed to subdivide a

possibly inﬁnite simulation domain into a regular

grid. Therefore, a hash function maps the three-

dimensional cells of the inﬁnite grid to an one-

dimensional hash-table of ﬁnite size (Teschner. et al.,

2003). For example, a point with position p = (x,y,z)

is hashed into a hash table of size m by computing its

cell index c as follows:

c =





∗ u



⊕





∗ v



⊕





∗ w



mod m,

where u,v,w are large prime numbers and d is the cell

size. If multiple points are hashed to the same hash

cell, chaining is employed to resolve hash collisions,

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

i. e. the points are stored in a linked list speciﬁc to this

cell. The parallel construction of such a hash table is

difﬁcult to realize. It would require serialization of the

access to the list structure if two points are hashed to

the same cell simultaneously. Frequent memory allo-

cations for the linked lists might be necessary if more

points move in and out of cells during the simulation.

(Teschner. et al., 2003) reserve a certain amount of

memory for each list during initialization to avoid this

problem, which is quite memory-inefﬁcient.

Cuckoo Hashing: A parallel hashing approach is

proposed in (Alcantara et al., 2009). It combines the

efﬁciency in construction time of the classical perfect

hashing scheme (Fredman et al., 1984) with multiple-

choice perfect ”cuckoo” hashing (Pagh and Rodler,

2004) that achieves high occupancy. The approach

employs a two-level construction. In the ﬁrst step,

the keys are hashed to a set of buckets. The buck-

ets are aligned in one large array B where all keys

within the same bucket are contiguous in memory.

Step two works on each bucket independently. The

multiple-choice hashing is performed on three hash

tables T

each with its own hash function. Each

bucket gets assigned a certain interval within the hash

tables. All keys within a bucket are hashed to the ﬁrst

hash table T

. If a hash collision occurs, the currently

processed key is stored in T

and the previously stored

key is kicked out. This is repeated iteratively for all

keys that are kicked out. In each iteration i, the re-

maining keys are stored in hash table T

, with j = i

mod d. It is likely that there is a key which is con-

stantly kicked out of the hash tables. If this is the case,

new hash functions have to be chosen and the process

has to be repeated entirely. With increasing hash ta-

ble size, this is becoming unlikely and negligible in

practice. The key value is the cell index. Naturally, as

the primitives within the same grid cell get the same

cell index, the approach has to be extended to multi-

valued hashing. Therefore, each key gets a counter

and an index pointer in order to know how many val-

ues it represents within the hash table and where to

ﬁnd those values within a secondary buffer array.

Discussion: The data structures of the compact grid

and cuckoo hashing are remarkably similar. The sec-

ondary buffer array resembles L and the hash tables

replace C. In contrast to the compact grid, C does not

scale with the simulation domain, but with the num-

ber of primitives. The array sizes for the buckets and

hash tables are reportedly chosen such that the occu-

pancy reaches 80% for the buckets and 70% for the

hash tables on average (Alcantara et al., 2009).

4 IMPLEMENTATION

The reduced memory requirements and the increased

efﬁciency of compact grids compared to basic uni-

form grids can be attributed to the fact that L is a static

array (Lagae and Dutr´e, 2008). However, the static ar-

ray demands a reconstruction from scratch in dynamic

scenes if the number of references to primitives varies

from frame to frame and, thus, changes the size of L.

In the following, we discuss three aspects related to

these arguments.

Cell Size: The cell size inﬂuences the number of

primitive pairs that have to be tested for intersec-

tion. However, it also inﬂuences the performance of

the sorting algorithm. The more cells the primitives

cover, the larger the data array and the lower the sort-

ing performance. In (Teschner. et al., 2003), it is sug-

gested that the average edge length of all tetrahedrons

should be chosen to achieve optimal performance. In

general, we stick to this recommendation. However,

if the tetrahedrons are close to regular, the maximal

edge length is chosen.

Parallel Sorting: The complexity and performance

of the compact grid construction are dominated by

the employed sorting algorithm. We tested a paral-

lel radix sort and a parallel re-implementation of the

sorting algorithm of the Standard Template Library

(STL) of C++. The last one is part of the OpenMP

Multi-Threaded Template Library (Yliluoma, ; Ope,

2005). Inherently, the radix sort does not take advan-

tage of pre-sorted sets of keys. Thus, its performance

is constant. On the other hand, the STL-sort beneﬁts

from sets of keys that are predominantly sorted. Such

sets appear if the spatial conﬁguration of objects in

a simulation domain is temporally coherent i. e. is

similar to the previous frame. In such a case, only

a small number of keys moves to new spatial cells.

A sorted set is quickly re-established. However, us-

ing STL-sort on a largely distorted set of keys might

prove to be slower than radix sort depending on the

input size. In such cases it might be beneﬁcial to em-

ploy the radix sort algorithm. Therefore, the amount

of distorted keys is determined by keeping track of

the primitives’ bounding boxes. If too many bounding

boxes move into new spatial cells, a threshold triggers

the switch to radix sort, and back. We discuss timings

for both sorting algorithms in the results section.

Z-curves: Primitives that intersect more than one

cell have to query the primitives stored in all the in-

tersected cells. It depends on the indexing function,

whether the order of the referenced primitives in L is

memory-coherent, i. e. are likely to be contiguous in

memory. Space-ﬁlling curves provide a solution to

EFFICIENT UNIFORM GRIDS FOR COLLISION HANDLING IN MEDICAL SIMULATORS

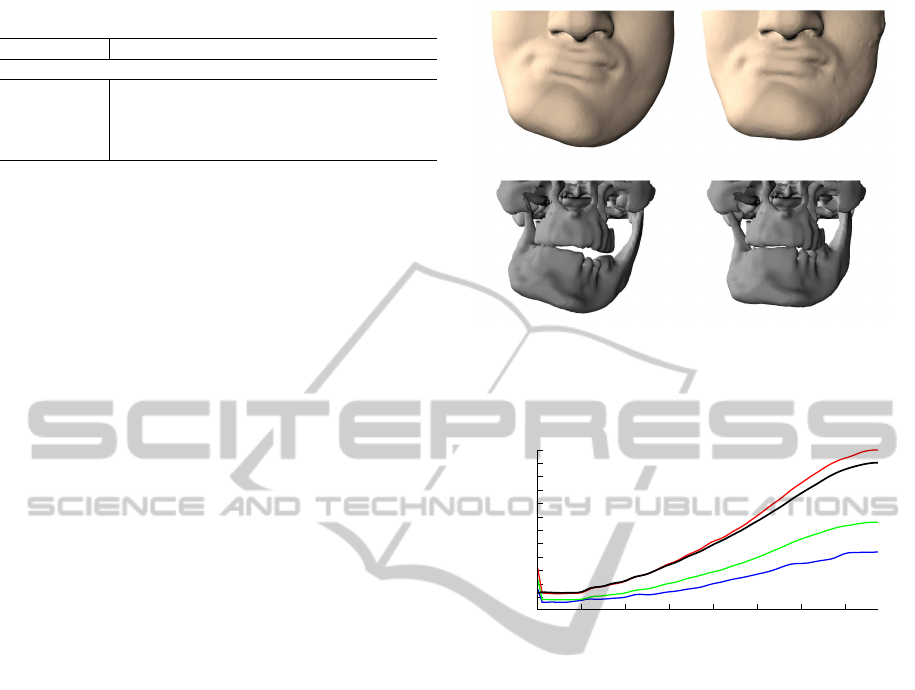
Table 1: Scene statistics for the three test scenarios.

stacking eye skull

scene statistics

#points 4840 3167 8293

#edges 19620 16248 38352

#tris 9600 6472 13592

#tetras 10000 9819 23225

this problem. They are a common tool in computer

science for mapping multidimensional data to one di-

mension while preserving spatial locality as good as

possible. We propose to employ the Lebesgue space

ﬁlling curve, also called Z-curve, to construct an ar-

ray C that is more spatially compact. They can be ef-

ﬁciently computed by bit-interleaving (Pascucci and

Frank, 2001).

5 RESULTS

We evaluate the performance of the presented meth-

ods in the context of interactive deformable modeling

using a set of test scenarios. Therefore, we have in-

tegrated the approaches into a deformable modeling

framework based on the Finite Element Method for

tetrahedrons in order to accelerate the collision han-

dling. The timings have been obtained on a com-

modity computer with one quad-core 2.66 GHz In-

tel Xeon E5430 CPU, 12 MB L2 cache and 4 GB of

memory. For the scaling experiments, a second com-

puter with two quad-core 3.16 GHz Intel Xeon X5460

CPUs, 2x6 MB L2 cache and 16 GB of memory has

been used. The number of cores is given with the tim-

ings, respectively. The methods are implemented in

high-level C++ with STL. No low-level optimization

such as SIMD is used. Parallelization of the code is

achieved using OpenMP (Ope, 2005).

Test Scenarios: The framework is applied to three

test scenarios. Their statistics are given in Table 1.

Stacking of deformable membranes is performed in

the ﬁrst scene. Here, the number of collisions in-

creases until all membranes are stacked up.

In the second and third scene, we apply the frame-

work to medical simulations. In the eye data set, the

interaction between skull, tissue, muscles, nerves, eye

bulb and titanium mesh is simulated. A titanium mesh

is used in orbital reconstruction to ﬁx fractures to the

orbital ﬂoor (see Figure 4). Thus, the eye bulb is repo-

sitioned. All objects are in constant interaction.

In the skull data set, the interaction of the soft tis-

sue with the skull, upper jaw and lower jaw is simu-

lated. The lower jaw is repositioned and the effect on

the skin tissue is simulated (see Figure 1).

Figure 1: The prediction of skin-tissue deformations due

to bone realignments supports the preoperative planning in

craniomaxillofacial surgery. The lower jaw is repositioned

and the effects on the skin tissue is computed.

100

110

120

0 100 200 300 400 500 600 700

computation time in ms

frame

Figure 2: Collision-handling timings for the stacking scene

using spatial hashing (black) and index sort with one (red),

two (green) and four (blue) cores.

Index sort vs. Serial Hashing: First, we compare the

parallel index-sort approach (IS) to the serial hashing

approach (SH) (Teschner. et al., 2003). We observe a

more efﬁcient update of the points stored in the static

array of IS when compared to the repeated insertion

of the points into the dynamic arrays within the hash

cells, even when using only one core. The query is

slower in IS when using one core, due to the standard

parallelization technique of adding one additional it-

eration to determine the size of the output array in

order to write out the collisions in parallel. However,

this is quickly compensated with each additional core,

see Figure 2. The ﬁrst frame shows a high initial com-

putation time, since the array L is sorted for the ﬁrst

time and spatial locality is established in L. The frame

rate stays interactive with the compact grid approach,

even when all membranes are stacked up.

Index Sort vs. Cuckoo Hashing: We set the size

of the buckets and the size of the hash table so that

an occupancy of 71% is achieved on average. Over-

ﬁlling of the buckets or hash collisons that enforces a

repeated insertion has never occured in our test runs,

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

100

0 100 200 300 400 500 600 700 800 900 1000

computation time in ms

frame

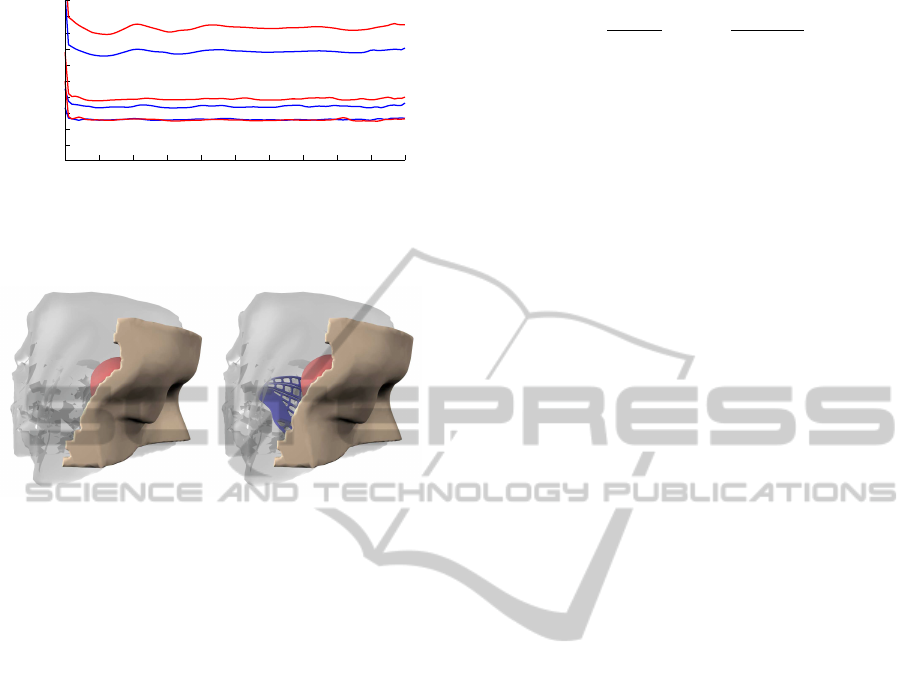
Figure 3: Timings for the eye scene using index sort (red)

and cuckoo hashing (blue) with one, four and eight cores.

Figure 4: Deformable modeling supports the preoperative

planning in craniomaxillofacial surgery. In orbital recon-

struction, a titanium mesh is placed beneath the bulb for

repositioning. All simulated objects are in constant inter-

action. The spatial conﬁguration only changes slowly over

time.

so we refer to the empirical results in (Alcantara et al.,

2009). The index sort approach again shows superior

insertion times with respect to points, but falls back

when inserting the footprints of a large number of col-

liding edges. On the other hand, the cuckoo hashing

introduces some overhead. This is due to the multiple

hash key computations for the three hash tables and

keys that iteratively have to ﬁnd an empty hash cell.

Performances are given in Figure 3.

Parallel Scaling: Ideally, the performance gain from

parallel algorithms should be linear in the number of

cores. However, this cannot be expected for several

reasons. First, there is some parallelization overhead

for synchronization and communication between dif-

ferent threads. Second, some parall algorithms have

to perform additional computations that only pay off

after providing a certain amount of additional cores,

e. g. additional loops over data arrays. Third, cer-

tain portions of an algorithm cannot be parallelized.

According to Amdahl‘s law, this limits the achievable

speedup (Amdahl, 1967). For example, if 90 percent

of the algorithm can be parallelized, the maximum

speedup is 10, regardlessof the number of cores. Note

that the law assumes that the problem size remains the

same when parallelized. The proportion of a program

that is run in parallel can be estimated using:

estimated

measured

− 1

#processors

− 1

. We

measure the speedup using the dual quad-core ma-

chine with all eight cores and get an average speedup

of 3.2 for the index sort approach and 2.6 for the

cuckoo hashing (based on the data shown in Figure 3).

Using the equation above, the estimated amount of

code is 80% for the index sort approach and 70%

for the cuckoo hashing approach. We see two resons

for these results. Regarding the index sort approach,

the STL-sort shows poor scaling behavior which leads

to a speedup of 1.5 for the update functions. This

is compensated by speedups of 5 in the query func-

tions. Regarding the cuckoo hashing, the work is dis-

tributed to the threads per bucket. When multi-value

hashing is performed, the ﬁxed size of the buckets’

hash tables leads to unequal work loads in the threads.

Dynamically sized tables would account for this, but

would require additional hashing to determine the ac-

tual number of values hidden behind the unique keys.

Sorting Performance: Two parallel sort algorithms

have been implemented. The results support the as-

sumptions made. For an input size of 128000 en-

tries in L, the radix sort takes 14ms on the 4-core

system. The STL-sort takes less than 6ms if 10%

of the keys change their value and 3ms for 2%. A

randomly ﬁlled array performs about equally in both

approaches. Thus, the STL-sort is always to be pre-

ferred for scenes with a complexity like the ones we

show here.

Z-curve Reordering: We employ Z-curves to in-

crease the spatial locality in memory. The index sort

only proﬁts marginally when rearranging L. However,

the query of edge-triangle intersections gets a perfor-

mance boost by about 8% on average. When query-

ing the intersection for one edge, the triangles that are

spatially close and likely to intersect are also close

in memory and likely to be already loaded into the

cache.

6 CONCLUSIONS

We have presented two acceleration data structures

based on uniform grids for the efﬁcient collision han-

dling in a deformable modeling framework. Impor-

tant aspects critical to the performance of such a sys-

tem were discussed. We have analyzed Z-curves for

the mapping of spatial locality to the grid represen-

tations. Further, the STL-sorting algorithm exhibits

better performance than the radix sort when applied

in the index sort approach. However, improved paral-

lel sorting algorithms have to be developed to achieve

EFFICIENT UNIFORM GRIDS FOR COLLISION HANDLING IN MEDICAL SIMULATORS

better speedups. We have analyzed the performance

aspects of the presented uniform grid approaches and

gave a detailed scaling analysis. The efﬁcient update

of the data structures as well as the efﬁcient query

speciﬁcally improve the performance in medical sim-

ulation scenarios where lots of collisions persist over

large time intervals.

ACKNOWLEDGEMENTS

This work has been supported by the German Re-

search Foundation (DFG) under contract numbers

SFB/TR-8 and TE 632/1-1.

REFERENCES

(2005). OpenMP Application Program Interface, Version

2.5. OpenMP Architecture Review Board.

Alcantara, D. A., Sharf, A., Abbasinejad, F., Sengupta, S.,

Mitzenmacher, M., Owens, J. D., and Amenta, N.

(2009). Real-time parallel hashing on the GPU. In

SIGGRAPH Asia ’09: ACM SIGGRAPH Asia 2009

papers, pages 1–9, New York, NY, USA. ACM.

Amdahl, G. M. (1967). Validity of the single processor ap-

proach to achieving large scale computing capabili-

ties. In AFIPS ’67 (Spring): Proceedings of the April

18-20, 1967, spring joint computer conference, pages

483–485, New York, NY, USA. ACM.

Bentley, J. L. and Friedman, J. H. (1979). Data structures

for range searching. ACM Comput. Surv., 11(4):397–

409.

Ericson, C. (2004). Real-Time Collision Detection. Morgan

Kaufmann.

Fares, C. and Hammam, Y. (2005). Collision detection for

rigid bodies: A state of the art review. In GraphiCon

2005.

Fredman, M. L., Koml´os, J., and Szemer´edi, E. (1984).

Storing a sparse table with 0(1) worst case access

time. J. ACM, 31(3):538–544.

Gissler, M., Schmedding, R., and Teschner, M. (2009).

Time-critical collision handling for deformable mod-

eling. Computer Animation and Virtual Worlds,

20:355–364.

Griebel, M. and Zumbusch, G. (1998). Hash-storage tech-

niques for adaptive multilevel solvers and their do-

main decomposition parallelization. In Domain de-

composition methods 10. The 10th int. conf., Boulder,

volume 218 of Contemp. Math, pages 279–286. AMS.

Hubbard, P. M. (1996). Approximating polyhedra with

spheres for time-critical collision detection. ACM

Trans. Graph., 15(3):179–210.

Kalojanov, J. and Slusallek, P. (2009). A parallel algo-

rithm for construction of uniform grids. In HPG ’09:

Proceedings of the Conference on High Performance

Graphics 2009, pages 23–28, New York, NY, USA.

ACM.

Kockara, S., Halic, T., Iqbal, K., Bayrak, C., and Rowe, R.

(2007). Collision detection: A survey. pages 4046

–4051.

Lagae, A. and Dutr´e, P. (2008). Compact, fast and robust

grids for ray tracing. Computer Graphics Forum (Pro-

ceedings of the 19th Eurographics Symposium on Ren-

dering), 27(4):1235–1244.

Levinthal, C. (1966). Molecular model-building by com-

puter. Scientiﬁc American, 214:42–52.

Lin, M. and Manocha, D. (2003). Collision and proximity

queries. In Handbook of Discrete and Computational

Geometry.

O’Sullivan, C. and Dingliana, J. (2001). Collisions and per-

ception. ACM Trans. Graph., 20(3):151–168.

Pagh, R. and Rodler, F. F. (2004). Cuckoo hashing. J. Al-

gorithms, 51(2):122–144.

Pascucci, V. and Frank, R. J. (2001). Global static in-

dexing for real-time exploration of very large regu-

lar grids. In Supercomputing ’01: Proceedings of

the 2001 ACM/IEEE conference on Supercomputing

(CDROM), pages 2–2, New York, NY, USA. ACM.

Rabin, M. O. (1976). Probabilistic algorithms. In Traub,

J. F., editor, Algorithms and complexity: new di-

rections and recent results, pages 21–39. Academic

Press, New York.

Tang, M., Curtis, S., Yoon, S.-E., and Manocha, D. (2008).

Interactive continuous collision detection between de-

formable models using connectivity-based culling. In

SPM ’08: Proceedings of the 2008 ACM symposium

on Solid and physical modeling, pages 25–36, New

York, NY, USA. ACM.

Teschner., M., Heidelberger, B., Mueller, M., Pomeranets,

D., and Gross, M. (2003). Optimized spatial hashing

for collision detection of deformable objects. In Vi-

sion, Modeling, Visualization VMV’03, Munich, Ger-

many, pages 47 – 54.

Teschner, M., Kimmerle, S., Heidelberger, B., Zachmann,

G., Raghupathi, L., Fuhrmann, A., Cani, M.-P., Faure,

F., Magnenat-Thalmann, N., Strasser, W., and Volino,

P. (2005). Collision detection for deformable objects.

Computer Graphics forum 24, 24(1):61 – 81.

Yliluoma, J. The openmp multi-threaded tem-

plate library. http://tech.unige.ch/ cvml-

cpp/source/doc/OMPTL.html.

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications