INTERACTIVE SIMULATION OF SHIP MOTIONS IN RANDOM

SEAS BASED ON REAL WAVE SPECTRA

José Miguel Varela and Carlos Guedes Soares

Centre for Marine Technology and Engineering, Technical University of Lisbon

Instituto Superior Técnico, Av. Rovisco Pais, 1049-001 Lisboa, Portugal

Keywords: Ship Motions, Interactive Simulation, Random Seas, Wave Spectra.

Abstract: The current paper presents a methodology to compute and represent the ship motions at interactive frame

rates, when navigating on a virtual sea defined by a real wave spectrum. The Inverse Discrete Fast Fourier

Transform algorithm is used to compute the sum of all ship motions components induced by the waves and

get the final irregular ship motion. Currently, this is the most efficient method to simulate the ship motions

in interactive ocean simulations using wave spectra to describe the sea states. The visual realism and

physical accuracy of the simulations turns this method into a powerful tool for developing interactive ship

simulators.

1 INTRODUCTION

Physically based ship motions simulation is a

fundamental task for ship simulators used as training

or as studying tools. In order to immerse the user in

the Virtual Environment as much as possible, these

tools require high levels of visual realism and

physical accuracy at interactive frame rates. In fact,

discrepancies between the sea state and the induced

ship motions, even if small, are immediately

detected by the user and the sense of immersion

decreases substantially. Moreover, if

manoeuvrability operations are to be studied with

the simulator, it is fundamental to preserve the

physical accuracy to obtain valid conclusions.

The method presented computes and simulates

interactively the ship motions induced by a random

sea surface based on a real wave spectrum. As the

surface may be deformed by thousands of wave

trains with different (small) amplitudes, frequencies

and directions of propagation, the method uses the

Inverse Discrete Fast Fourier Transform (IDFFT)

algorithm to compute the final ship motion, which is

given by the sum of all the singular motions induced

by each wave component. As a result, the method

allows simulating the ship motions in a virtual sea

surface that can be deformed by a large number of

waves increasing not only the visual realism but also

the physical accuracy of the simulation. By

establishing and maintaining the synchronism

between the phases of wave trains and ship motions,

the method allows simulating the motions for any

ship position, speed and heading. In order to test the

method, an ocean generator software system was

developed, which creates virtual sea surfaces based

on the random sea concept. Then, transfer functions

of a LNG ship, which describe how the ship reacts to

forces generated by wave trains with different

properties, were used to apply the method for

different sea states and manoeuvrability conditions.

Good results were obtained from the performance

and realism points of view in which the ship motions

are coherent and realistic even for stormy seas

composed by thousands of wave trains.

The remaining of the paper develops as follows:

section 2 provides some background on the sea

surface generation and on the consequently induced

ship motions computation; section 3 describes the

method used to compute and simulate the ship

motions; section 4 presents implementation details

of the method in a prototype software system;

section 5 discusses the results; section 6 presents the

methodology used to validate the results and finally

the main conclusions are presented in section 7.

2 BACKGROUND

Ship motions are represented by six main

components corresponding to the six degrees of

235

Miguel Varela J. and Guedes Soares C..

INTERACTIVE SIMULATION OF SHIP MOTIONS IN RANDOM SEAS BASED ON REAL WAVE SPECTRA.

DOI: 10.5220/0003324502350244

In Proceedings of the International Conference on Computer Graphics Theory and Applications (GRAPP-2011), pages 235-244

ISBN: 978-989-8425-45-4

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

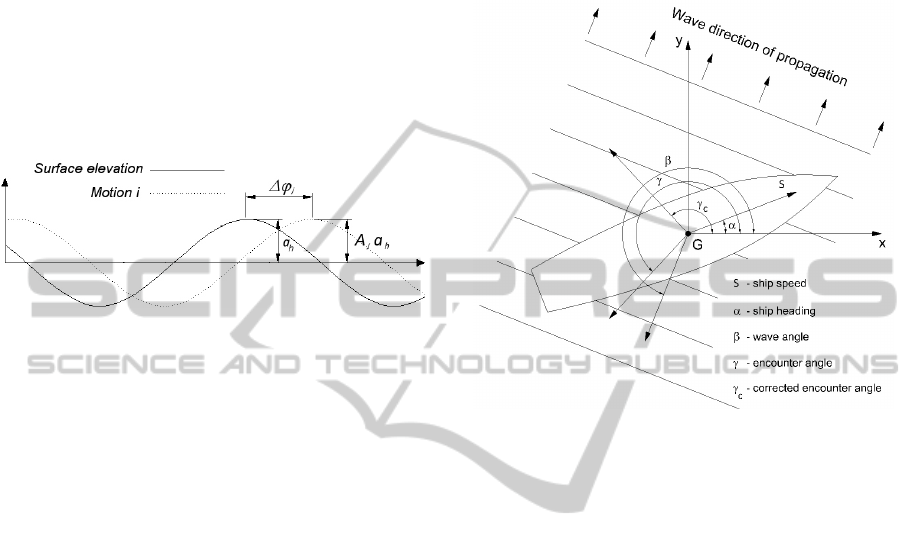
freedom in the 3D space, as presented in figure 1.

Figure 1: Ship motion is divided into six components in

the six degrees of freedom.

Surge, sway and heave correspond to the

translation motions along the x, y and z axis

respectively, while roll, pitch and yaw are the

rotation motions also in the x, y and z respectively.

Most of the ship motion simulators running on

desktop computers do not actually compute the

motions in real-time. Depending of the purpose of

the simulator, ship motions may be computed

previously, and the Virtual Environment (VE) works

as a post-processing visualization and interaction

tool for the simulation. Databases store the ship

motions’ parameters for different wave patterns, and

the data is then queried (in database) and applied in

real-time. It is the case of Daqaq (2003), in which

the ship motion must be realistic in order to test

loading and unloading operations.

Simulation models that compute ship motions in

real time such as Xiufeng et al. (2004) or Sutulo et

al. (2002), normally do not compute wave induced

motions and only the three degrees of freedom

corresponding to the surge, sway and yaw in the

manoeuvrability equations are considered. Such

tools are used to simulate port operations where the

motions induced by the sea waves (heave, roll and

pitch) are negligible. Although three of the ship

motions are not computed, these simulators include

manoeuvrability models to calculate ship trajectories

that consider the interaction between the water, the

sea bottom (shallow waters) and coastal structures

(walls, berths, etc.), which increases the

computational work required, Sutulo et al. (2010).

In an attempt to compute the six motion

components in real time, simplified models such as

Ueng et al. (2008) have been developed. They use a

moving grid attached to the ship generated by the

vertical projection of the ship’s body into the

horizontal plane. The bounding box of the projection

is used and a uniform grid of cells is superposed on

the bounding box. Then the height field of the sea

surface is evaluated at each grid point and the

average height field is multiplied by the area of the

grid to compute the excitation force of water. For

each ship motion component, resistance forces are

estimated and the net force is obtained by

subtraction. Accelerations are then calculated by

applying the Newton’s second law.

Another approach to estimate the ship motions

induced be sea waves is by computing commonly

called Response Amplitude Operators (RAOs). In

linear theory, ship motions are calculated as the

finite sum of sinusoidal components with a random

initial phase, Bhattacharyya (1978). The amplitude

of each of the components is given by RAOs that

define the relationship between ship motion and

wave height versus regular wave frequency, Lewis

(1988). RAOs may be obtained by wave tank

experiments with scale models of the ships or may

be computed by specialized software. The strip

theory is the common approach to compute the

RAOs of the ships for the six degrees of freedom,

Salvesen et al. (1970). This theory assumes the ship

as a slender body and includes ship motion

coefficients such as added mass and damping in

heave and pitch motions. Numerous comparison

studies showed that strip theory generally gives good

results for ship motions in low to moderate regular

waves in which the influence of nonlinearities is still

low. However, Fonseca and Guedes Soares (1998)

presented a generalization of the theory to deal with

large amplitude motions.

Pre-calculated RAOs, which are defined for each

particular ship hull with specific cargo conditions,

allows to compute the amplitudes of each ship

motion component in frequency domain for

predefined manoeuvrability conditions (ship speed

and heading) and sea states (frequency and direction

of propagation of the wave trains). The conversion

of the ship motion component from frequency to

time domain, which is the one of interest for the

interactive simulation, takes into consideration the

phase of each wave when it reaches the ship. In

order to achieve a consistent and physically correct

motion in time domain, the phase of each ship

motion component and the phase of the

corresponding wave train must maintain the

relationship given by the RAO. The final motion is

given by the sum of all the ship motions generated

by all the wave trains.

Each ship motion component is given as a

periodic function in time of the following type:

(

)

iiii

tax

sin

(1)

where i corresponds to one of the motion types, x

is

the ship motion of type i, a

is the amplitude of the

motion derived by the RAO, ω

is the frequency of

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

236

the motion, t is the time and φ

is the phase

difference between the ship motion and the wave

train motion. This last value is also pre-computed by

transfer functions that depend of the ship

hydrodynamic properties. Naturally, these RAOs are

only computed for a certain number of ship speeds

and headings, and for a limited range of wave trains’

frequencies and directions of propagation. Hence,

for intermediate values interpolations are normally

applied. Examples of comparison of numerically

simulated motions with measurements can be found

in Fonseca and Guedes Soares (2002).

As the ship motions are mainly induced by ocean

waves, the simulation of the sea state must be also

realistic from the physical point of view. Currently,

interactive simulations of ocean waves for Virtual

Environments apply the concept of random seas

based on wave spectra. This method allows creating

a statistically valid irregular sea surface with very

good visual appearance that may run at interactive

frame rates with modern CPUs.

Random seas are composed by a large set of

wave trains whose properties, namely the amplitude,

frequency and direction of propagation, are taken

from the discretization of a directional wave

spectrum. Wave spectra are estimated from

measurements of the surface elevation on ocean. The

signal in time domain is converted to frequency

domain by applying the Discrete Fourier Transforms

(DFT). Therefore, in order to convert back the

signals to time domain, Inverse Discrete Fourier

Transforms (IDFT) are applied to the wave trains

defined by the spectrum.

In random seas simulations, each wave train

obtained from the spectrum discretization, imposes a

small deformation into the sea surface. The final

deformation is given by the sum of all the

components. The main drawback of this procedure is

that for every vertex of the surface the elevation of

the sea must be evaluated by the sum of the

deformations imposed by of all the wave trains at

that vertex. As the number of waves must be quite

large in order to achieve a statistically valid and

visually realistic simulation, the calculation easily

becomes unsuitable for interactive simulations. The

solution adopted currently is to use the IDFFT

algorithm, which is an optimized form of the IDFT

to compute the sum of all the deformations on every

vertices of the sea surface. This solution imposes

some restrictions to the spectrum discretization and

to the distribution of the surface vertices in space. It

is out of the scope of this work to go deeply on this

issue, however, the relevant aspects that result from

use of the IDFFT algorithm to generate and simulate

the sea surface are the following:

 The sea surface is a regular grid with NxM

vertices (normally with N=M), where N and M

are power of 2.

 Wave vectors represented by the sea surface

depend of the location of each vertex of the

grid. Since the central vertex of the grid is

located at

(

)

0,0

, there are wave trains

propagating in all the directions with different

lengths. The wave number is given by the

length of the wave vector and therefore there

are also wave trains with different lengths.

Consequently, by the relation of dispersion,

wave trains also have different frequencies.

 From the previous point, the maximum

number of represented wave trains is equal to

NxM‐1. The only wave that cannot be

represented is the one derived from the central

vertex because its wave number is equal to

zero.

 Although all the waves defined by the grid

vertices may be represented, in most of the

cases there is a large number in which the

amplitude derived from the spectrum

discretization is equal to zero.

Goda (2000) provides the general theory of wave

mechanics for simulating random seas while

Tessendorf (2001), Belyalev (2003) and Fréchot

(2007) are good references focused on the

generation and simulation of random seas at

interactive frame rates.

3 COMPUTATION OF THE SHIP

MOTIONS

3.1 The RAO Operator

The computation of the ship motions in time domain

is intrinsically related with the wave trains

represented by the ocean grid in the sense that each

wave train generates six components of the ship

motion given by equation 1. The relation between

the properties of each function is obtained by the

RAOs of the ship.

Let h

,ω

,φ

,t) be the function describing the

surface elevation at time instant t due to the wave

train i, and m(t) the value of the generated ship

motion function also at instant time t. Each

component j of the ship motion m(t) is given by:

INTERACTIVE SIMULATION OF SHIP MOTIONS IN RANDOM SEAS BASED ON REAL WAVE SPECTRA

237

(

)

()

[]

tahRAOtm

hhhijj

,,,

(2)

where the operator RAO

specifies the relation

between the values of the amplitudes, a

frequencies, ω

, and initial phases, φ

of the wave

train function and the homologous values of the

component

of the generated ship motion.

In linear theory, the ship motion generated by

each wave train is also described by a sinusoidal

function with the same frequency but with different

amplitude and phase as shown in figure 2.

Figure 2: Relation between the ship motion component

and the surface elevation for a single sinusoidal wave in

linear theory.

The frequency of the ship motion is the same as

the frequency of the wave train, so equation 2 can

then be written in its sinusoidal form:

()

(

)

jhhhjj

taAtm

Δ++= sin

(3)

where A

and Δφ

are the pre-calculated values

specified by RAO

for different ship speeds and

angles, and for different frequencies of the wave

trains.

For a specific ship heading, the encounter angle

used to find the correct RAO

must take into

consideration the direction of propagation of the

wave train as presented in figure 3, Guedes Soares

(1995).

The encounter angle is given by:

−=

(4)

where α is the ship heading and β the wave angle.

Due to the longitudinal symmetry of the hull of

almost all the existent vessels, encounter angles

specified in the RAOs are only applied to portside

and therefore they are defined in the interval [0,π].

On the other hand, wave angles and ship headings

are defined in the interval [0,2π] and therefore if the

encounter angle lies between π and 2π, which is the

example case of figure 3, it must be corrected by the

expression:

(

)

−

(5)

Having the current ship speed and the corrected

encounter angle, the values of A

and Δφ

can be

easily derived from the RAOs tables.

Figure 3: The encounter angle is given by the difference

between the wave angle and the ship heading.

3.2 Interpolations between RAO

Values

As mentioned, RAO values are specified for specific

vessel speeds, encounter angles and wave

frequencies. However, in a generic simulation, the

manoeuvrability conditions of the ship (speed and

heading) or the sea state do not necessarily (and

most of the time they do not) coincide with the

specified RAO values. For such cases, interpolations

must be performed in order to find the correct RAO

values for the current ship and sea states.

Figure 4 represents schematically the data

contained in the RAOs tables from which the

simulation reads the values for the motion

amplitudes and phases depending of the current

status of the ship and the sea state.

When the manoeuvrability values are between

the specified ones, linear interpolations are

performed to get the real amplitudes and phase

angles. In order to compute by interpolation the final

values of Aj and Δφj for each motion mj, the

following arrays are stored in memory:

 The speed table, s_Tb, contains N lines and

two columns. Each line corresponds to a ship

speed computed in pre-calculations. The first

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

238

column is filled with the speeds in which

s_Tb[0,0]=0.0 and s_Tb[N,0] is the maximum

speed of the ship. The second column is

associated to an encounter angle table for each

ship speed.

 The encounter angle table, γ_Tb, contains M

lines and two columns. Each line corresponds

to the encounter angles computed in pre-

calculations. The first column is filled with the

encounter angles in which γ_Tb[0,0]=0.0˚ and

γ_Tb[M,0]=180.0˚. The second column is

associated to a wave frequencies table for each

encounter frequency.

 The wave frequencies table, ω_Tb, contains P

lines and two columns. Each line corresponds

to the frequencies computed in pre-

calculations. The first column is filled with the

frequencies in which ω_Tb[0,0] is the

minimum wave frequency and ω_Tb[P,0] is

the maximum wave frequency computed. The

second column is associated to the motions

table for each frequency.

 Finally the motions table, m_Tb contains 6

lines and 2 columns. Each line corresponds to

one of the six components of the motion. The

first column stores the amplitude ratio, Aj, and

the second column the phase difference, Δφj,

values for the motion.

Let s and γ be the ship’s speed and encounter

angle respectively at time t, in a wave train of

Figure 4: RAOs values are read from ASCII files and

stored in hierarchical tables.

frequency ω. The values of speeds, encounter angles

and frequencies specified in the RAOs tables that

will be of interest to perform the necessary

interpolations to compute the final parameters A and

Δφ of the ship motion component are:

[

]

1,0,0,_ =

iinTbss

(6)

where, n is the index corresponding to the speed

immediately below s in the speed table.

[

]

1,0;1,0,0,_ ==

jijmTb

iij

(7)

where,

m is the index corresponding to the encounter

angle immediately below

γ in the encounter angle

tables and γ

_Tb

=S_Tb[n+i,1].

[

]

1,0;1,0;1,0,0,_ ==

kjikpTb

ijijk

(8)

where,

p is the index corresponding to the wave

frequency immediately below

ω in the wave

frequency tables and

ω_Tb

=γ_Tb

[m+j,1].

Three factors,

s_fact, γ_fact and ω_fact are

computed to interpolate between ship speeds,

encounter angles and wave frequencies respectively.

The speed factor

s_factЄ[0,1] is computed by

the expression:

[]

[] []

0,_0,1_

0,_

nTbsnTbs

nTbss

facts

−+

−

(9)

The heading factor

γ_factЄ[0,π] is computed

by:

[]

[] []

0,_0,1_

0,_

mTbmTb

mTb

fact

γλ

−+

−

(10)

The frequency factor

ω_factЄ[ω

min

,ω

max

] is

computed by:

[]

[] []

0,_0,1_

0,_

0000

pTbpTb

pTb

fact

ωω

−+

−

(11)

Finally, being m the value of A or Δφ specified

in the motions table for a specific component the

ship motion,

m is calculated by the following

expression:

(

)

010

_ mmfactsmm −

(12)

where the following equations apply:

(

)

010

iiii

mmfactmm −

(13)

(

)

010

ijijijij

mmfactmm −

(14)

INTERACTIVE SIMULATION OF SHIP MOTIONS IN RANDOM SEAS BASED ON REAL WAVE SPECTRA

239

[]

2,1r,,_ =+= rkpTbm

ijijk

(15)

For

r=1 (second column) the corresponding A

value is computed while for

r=2 (third column) the

value of

Δφ is calculated.

As a simplification, the centre of rotation of the

ship is the centre of buoyancy and remains

unchangeable during the simulation.

3.3 The FFT Algorithm

After computing the values of A and Δφ for all the

ship motions, evaluating at interactive frame rates

the six components of the final ship motion at instant

time

t as the sum of all the motions generated by all

the wave trains is only possible using the IDFFT

algorithm. As an example for an ocean grid with

128x128 vertices and therefore 16383 wave trains

(applying the random sea model mentioned in

section 2), a total of

6x16383=98304 ship motions

may have to be evaluated every frame. Taking into

consideration that each ship motion is described by a

circular sinusoidal function, this sum can rapidly

lead to unacceptable frame rates.

The IDFFT algorithm provides an efficient way

to compute the following sum:

∑∑

⎟

⎠

⎞

⎜

⎝

⎛

mnqp

eFf

(16)

where

n,m

is a set of complex numbers uniformly

distributed and

∈

{1,…,N} and q

∈

{1,…,M}.

From the application of the IDFFT algorithm to

the random sea model, the elevation of the water

surface as the sum of the elevations generated by all

the wave trains at a grid point

p,q

=(p‐N/2,q‐M/2), is

given by:

(

)

()

∑∑

−

Re12

mqnp

eea

tgh

ϕω

(17)

where

and φ

are also evaluated for the wave train

corresponding to the grid point

p,q

If the position of the ship is added to equation 3,

each ship motion is described in complex notation

by the following expression:

(

)

()

ishh

hii

eaAtm

ϕϕϕω

Δ+++

(18)

where

is the phase term which depends of the

ship position in the grid.

Therefore, from equation 17 and 18, the ship

motion at the grid point

p,q

=(p‐N/2,q‐M/2), is given

by:

(

)

()

∑∑

−

Δ+++

−

Re12

mqnp

qpi

eeaA

tgm

ishh

ϕϕϕω

(19)

Equation 19 has the form of equation 16 and

therefore the IDFFT algorithm can be used to

compute the sum of the ship motions at each grid

vertex. In equation 19 the parameters A

and Δφ

are

computed from equation 12;

, ω

and φ

are taken

from the wave trains.

The value of

depends of the ship position and

is given by:

(

)

shhs

xkk

⋅=

(20)

where

is the wave number of the wave train, ||

is the normalized direction of propagation vector of

the wave train and

is the ship position in the grid.

3.4 The Ship Position in the Grid

The term φ

appears because the ship most probably

will not be positioned on the grid vertices which are

the locations where the motions are computed.

Therefore an additional phase term must be added. It

depends of the ship position in the grid,

, namely

the position relatively to the vertex where the ship

motion is computed.

Figure 5: The ship position in the grid

is required to

compute the phase term φ

of the ship motion.

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

240

If the ship is in the position

p, as shown in figure

5, then the ship motions are evaluated at vertex

p,q

and the vector

is used to compute the phase term

4 IMPLEMENTATION

A prototype system was developed to test the

method described. The system generates a virtual

random sea based on the parametrical wave

spectrum of JONSWAP type. The user selects the

size and the resolution of the ocean grid and then

applies the spectrum to the grid generating a virtual

ocean. The characteristics of the spectrum are also

defined by the user, namely the wind speed, fetch

and main direction of propagation. The first two

parameters allow generating calm or rough seas with

more or less predominance of swell waves.

After the ocean is created, the system loads a

ship with a geometric definition and an associated

physical behaviour described in ASCII files. The

RAO arrays are created from the data contained in

the files.

Figure 6 presents the UML class diagram of the

ship.

The class Ship is a SceneNode with a

geometrical representation located and oriented in

the tri-dimensional space. It points to a number of

ship motions equal to the number of wave trains in

the virtual ocean. Each ship motion has a pointer to

its corresponding wave train and uses the

information stored in the RAO tables, combined

with the properties of the wave train, to compute its

amplitude, frequency and initial phase. This last

depends of the phase difference specified in the

RAO tables and of the position of the ship in the

grid.

Figure 6: UML Class Diagram of the Ship.

As can be seen, the simulation uses only one

time, which is stored by the ocean object. All the

other objects use this simulation time to perform the

calculations.

Figure 7 presents the UML Activity Diagram for

a single frame.

The first task that must be performed before any

other operation take place, is the update of the

simulation time because its value is used on both the

ocean and ship operations. After that, activities

performed in the ocean and in the ship may run in

parallel because they are independent.

The updated time allows the ocean to calculate

for every wave train the elevation on each vertex of

the grid. Then the FFT algorithm is used to compute

the sum of all the elevations of every point of the

grid and finally all the vertices are updated to new

positions. Update the ship motions consists in

performing the interpolations in the RAOs tables in

order to compute the amplitude and phase difference

for all the ship motions. Then, the ship is moved

horizontally to its new position according to its

speed and heading. The new location allows

computing the ship position in the grid, which is

necessary to calculate the value of

in equation 20.

With all the ship motions’ parameters calculated, the

FFT algorithm is then applied to compute the sum of

all the ship motions in the point where the ship

stands. Finally the position and orientation of the

ship are again updated to the final status.

The system was developed on the top of the

OGRE3D (Object-oriented Graphics Rendering

Figure 7: UML Activity Diagram for a single frame.

INTERACTIVE SIMULATION OF SHIP MOTIONS IN RANDOM SEAS BASED ON REAL WAVE SPECTRA

241

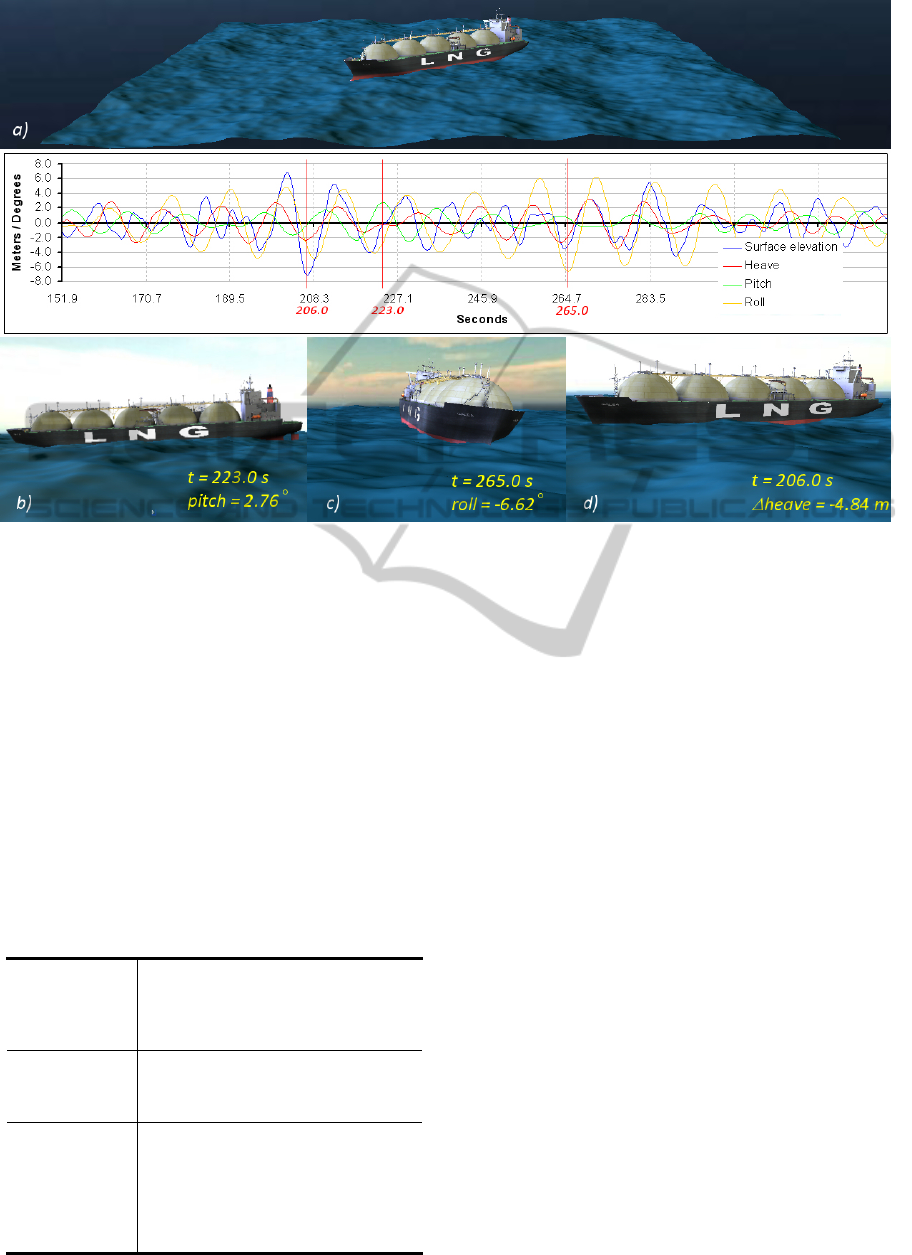
Figure 8: Results of the simulation with the parameters and characteristics presented in table 1.

Engine - http://www.ogre3d.org/) and the FFT

calculations were performed using the FFTW library

(Fastest Fourier Transform in the West -

http://www.fftw.org/).

5 RESULTS

Simulation tests were conducted in a Pentium(R)

Dual Core CPU E5200 @ 2.50GHz (2 CPUs) with

3070MB RAM. The graphics card was a NVIDIA

GeForce 9600 GT with 1024.0 MB RAM.

Figure 8 presents screen captures of a simulation

with the characteristics specified in table 1.

Table 1: Simulation parameters.

Seastate

Beaufortwindscale……….....9

Significantwaveheight.…...9.0m

Fetch………………...……….…367.6km

Peakfrequency……..….………0.5rad/s

Oceangrid

Resolution…………………………256x256

Sidelength……………….….......637.5m

Nºofwaves(a>0.0m)..……..18829

Ship

Type…………………………………..LNG

Lengthoverall…………………….290.0m

Breadth……………………………..…46.0m

Depth…………………..................25.5m

Draught…………………….…………11.4m

Speed………………....................19.8kn

For the simulation presented in figure 8, waves

are mainly coming from portside and stern. In figure

8a) it can be seen the irregular appearance of the sea

surface due to the high number of represented

waves. The graph of figure 8 represents the sea

surface elevation and the three most visible motion

components of the ship along time. Three screen

captures are presented in different instants of the

simulation in which one of the motion components

reach high values. In figure 8b) the ship is trimmed

with the stern raised and part of the rudder out of the

water. Figure 8c) emphases the roll motion to

portside and finally figure 8d) shows the difference

between the heave and the surface elevation at

amidships.

From the performance point of view, a frame

rate of approximately 9 fps was achieved in the

simulation of table 1. It is still below the necessary

frame rate required for interactive applications.

However, if the resolution of the ocean grid to is

reduced to

128x128, the frame rate increases to 26

fps which is already an acceptable value. Therefore

and as expected, the grid resolution is a determinant

factor for the performance of the simulation. Figure

9 presents a screen capture of the same sea state but

with an ocean resolution of

128x128 with the same

side length.

Although it is clear that the grid resolution of

256x256 presents more realistic results of the ocean,

because the number of waves is significantly higher,

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

242

the

128x128 grid does not stay far behind.

However, it is expectable that interactive frame

rates can be achieved with

256x256 grid resolutions

using a more powerful CPU already available at

affordable prices.

All the calculations were preformed on the CPU.

However, studies like Moreland and Angel (2003)

allow computing the FFT on the GPU. As the sea

surface height field and the ship motions numerical

simulations are heavily based on the FFT, it is

expected that the frame rate increases substantially if

these calculations are performed on the GPU.

Figure 9: Ocean appearance for a simulation with a

128x128 grid resolution.

6 VA L I D AT I O N

When the virtual sea state is composed by thousands

of wave trains with different amplitudes, frequencies

and directions of propagation, it is impossible to

verify if the ship motions are absolutely coherent

with the surface deformation.

Therefore some features were added to the

system to artificially change the sea state and

consequently the ship motions, but maintaining the

same method of computation.

The first feature was to reset to 0.0 all the

amplitudes of the wave trains with the exception of

one whose frequency and direction of propagation

was (obviously) known. Then a feature to assign

specific amplitude to this wave train was added. By

doing this, the ship motions are computed using the

method described for all the wave trains, but only

one wave actually generates the ship motions. In

such situation it was possible to verify if the ship

motion was coherent with the deformation of the

surface. The possibility of only representing

specified components of the ship motion (surge,

heave, roll, etc.) was also added. Therefore the

results of each separated component when subjected

to a single wave train were analysed.

Using these features, several tests were

performed with different wave trains, for specific

components of the ship motion and for different

speeds and encounter angles.

Although it is difficult to represent the validation

tests (which are mainly based on animations) in the

paper, we present screen captures and ship motions

graphs in figures 10 and 11 for some of the

simulations performed.

The wave train used for validation purposes had

the lowest frequency of all the waves represented by

the ocean grid. An amplitude of 10.0 meters was

artificially assigned in order to increase and observe

the ship motions clearly. For lower frequency wave

trains, heave motions are almost synchronized with

the surface elevation at amidships. This can be

verified by the graph presented in figure 10.

Figure 10: Ship subjected to a single wave train coming

from steam with an amplitude of 10.0 m, frequency equal

to 0.310 rad/s and wavelength of 640 m.

The pitch motion has a phase difference of nearly

90˚, which also validates

the results. In fact when the

surface elevation is minimum (at the wave though),

for instance at t≈86s, the pitch angle is around 0.0˚.

This is the moment when the surface elevation is

nearly the same at the stem and at the stern and that

is why there is no pitch angle. When the surface

elevation increases at amidships, the difference

between elevations at the stem and stern also

increases the pitch angle decreases leading the stem

to rise (see figure 1). The minimum value of pitch

occurs when the elevation is nearly zero at

amidships, which is when the ship is half way

between the though and the crest of the wave.

With low frequency wave trains coming from

starboard, the sway and roll motions present similar

behaviour to the pitch motion as shown in figure 11.

As expected, both graphs in figures 10 and 11

have the same configuration of the graph presented

in figure 2 in which the frequency of the motions

and the surface elevation is the same, and there is a

phase difference given by the RAOs of the ship.

INTERACTIVE SIMULATION OF SHIP MOTIONS IN RANDOM SEAS BASED ON REAL WAVE SPECTRA

243

Figure 11: Ship subjected to a single wave train coming

from starboard with amplitude of 10.0 m, frequency equal

to 0.310 rad/s and wavelength of 640 m.

7 CONCLUSIONS

A method to simulate the ship motions in the six

degrees of freedom at interactive frame rates in an

irregular sea state based on a real wave spectrum

was presented. In order to achieve interactive

performance, the IDFFT algorithm must be used to

compute the sum of all the ship motions generated

by the wave trains. Even so, the maximum

resolution allowed with the hardware available today

is 256x256 if the calculations are performed in the

CPU. The ship motions obtained with this method

are visually coherent with the irregular sea state

simulated; however, it was necessary to validate the

results by applying the method for situations in

which the ship is subjected to a single wave train of

low frequency.

This method can be applied in simulation tools

that require visual a physical realism of the sea and

the ship motions at interactive frame rates such as

ship simulators.

REFERENCES

Bhattacharyya, R. 1978. “Dynamics of Marine Vehicles”,

John Wiley & Sons Inc.

Belyalev, V. 2003. “Real-time simulation of water

surface”, In: GraphiCon-2003, Conference

Proceedings, pages 131–138. MAX Press.

Daqaq, M. 2003. “Virtual Reality Simulation of Ships and

Ship-Mounted Cranes”, MSc Thesis. Faculty of the

Virginia Polytechnic Institute and state University.

Blacksburg, Virginia.

Fonseca, N., and Guedes Soares, C., 1998. “Time-Domain

Analysis of Large-Amplitude Vertical Motions and

Wave Loads”, Journal of Ship Research, Vol. 42, Nº

2, pp. 100-113.

Fonseca, N. and Guedes Soares, C., 2002. “Comparison of

Numerical and Experimental Results of Non-Linear

Wave Induced Vertical Ship Motions and Loads”,

Journal of Marine Science and Technology, vol. 6, pp.

193-204.

Fréchot, J., 2007. “Realistic Simulation of Ocean Surface

Using Wave Spectra”, Journal of Virtual Reality and

broadcasting, vol. 4, nº 11.

Goda, Y., 2000. “Random Seas and design of maritime

structures”, Advanced Series on Ocean Engineering,

World Scientific, vol. 15, ch. 2.

Guedes Soares, C., 1995. “Effect of Wave Directionality

on Long-Term Wave Induced Load Effects in Ship.”

Journal of Ship Research, vol. 39 nº 2, pp. 150-159.

Lewis, E.V. (Ed.). 1988. “Principles of Naval Architecture

Vol. III: Motions in Waves and Controllability” 3

ed.

Society of Naval Architects and Marine Engineers,

New York.

Moreland, K. and Angel, E., 2003. “The FFT on a GPU”,

HWWS'03 Proceedings of the ACM

SIGGRAPH/EUROGRAPHICS conference on

Graphics Hardware, 26-27 July, San Diego, CA,

USA, pp. 112-119.

Salvesen, N., Tuck, O.E. and Faltinsen, O., 1970. “Ship

motions and sea loads”, Transactions, Society of Naval

Architects and Marine Engineers, no. 78, pp. 250-

287.

Sutulo, S.; Moreira, L., and Guedes Soares, C., 2002.

“Mathematical Models for Ship Path Prediction in

Manoeuvring Simulation Systems”, Ocean

Engineering, vol. 29, nº 1, pp. 1-19.

Sutulo, S.; Rodrigues, J. M., and Guedes Soares, C., 2010.

“Hydrodynamic Characteristics of Ship Sections in

Shallow Water with Complex Bottom Geometry”,

Ocean Engineering. vol. 37, pp. 947-958.

Tessendorf, Jerry, 2001, “Simulating Ocean Water”,

SIGGRAPH 2001, course notes.

Ueng, Shyh-Kuang; Lin, David and Liu, Chieh-Hong,

2008, “A ship motion simulation system”, Virtual

Reality, vol. 12, pp. 65-76.

Xiufeng, Zhang; Yicheng, Jin; Yong, Yin and Zhihua, Li.

2004. “Ship Simulation Using Virtual Reality

Technique.”, Proceedings of GRAPHITE 2004. 15-18

June, Singapore.

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

244