
GENERATION OF FACIAL IMAGE SAMPLES FOR BOOSTING
THE PERFORMANCE OF FACE RECOGNITION SYSTEMS
Zhibo Ni and C. H. Leung
Department of Electrical and Electronic Engineering, Univerisity of Hong Kong, Pokfulam Road, SAR, Hong Kong
Keywords: Face matching, Morphing, Virtual samples, Face recognition.
Abstract: We tackle the problem of insufficient training samples which often leads to degraded performance for face
recognition systems. First, we propose an efficient method for matching two facial images that does not
require 3D information. We then apply the proposed face matching algorithm to morph a source image into
a target image, thereby generating a large number of facial images with expressions or lighting conditions
in-between that of the source and target images. These generated images are used to greatly expand the set
of training samples in a face recognition system. Experiments show that by incorporating these large
number of generated facial images in the training process, the recognition rate for test samples is boosted up
by a large margin.
1 INTRODUCTION
Appearance-based approaches such as principle
component analysis (PCA) and linear discriminant
analysis (LDA) are useful for face recognition. For
statistical accuracy, a large number of training
samples is desirable, but this condition is often not
met. One remedy is to generate additional distorted
samples by adding noise, mirroring an image, etc.
These simple methods are helpful but the variations
achieved are not enough and the generated faces
look unnatural. More sophisticated methods have
been proposed such as the flexible active shape
models (Lanitis, Taylor, and Cootes, 1997) and
active appearance models (Cootes, Edwards, and
Taylor, 2001). One potential drawback of using
perturbations is the possibility that the generated
faces are highly correlated, as reported by Martinez
(Martinez, 2002). To avoid such correlations, our
proposed method uses image morphing to generate
new training samples directly. Existing methods
(Vetter and Poggio, 1997) use 3D models but the
computational complexity is high. Our proposed
method requires only 2D images. It is simple and the
computational cost is low. By augmenting the
training set with a large number of generated
training samples, we can take full advantage of
statistical pattern recognition methods and use more
sophisticated classifiers.
2 ELASTIC MATCHING AND
IMAGE MORPHING
Given a face image, the face region is roughly
located, and the locations of the eyes, nose and
mouth are determined. Edge detection is performed
in these regions, and the detected edges are sampled
and represented by a number of points. These points
constitute the feature points for elastic matching, as
illustrated in Fig. 1(a).
Elastic matching is done to match the feature
points of two images. The algorithm employed is
adapted from that proposed by one of the authors in
(Li, Leung, and Hung, 2004) for stereo matching,
which is partly based on the algorithm for solving
the traveling salesman problem (Durbin and
Willshaw, 1987). It is quite efficient since it does
not involve face modeling, and works only in 2D.
The elastic matching is done in a coarse-to-fine
manner. In each iteration, the feature points in the
source image are moved closer towards the
corresponding positions in the target image. Let {A
j
| j = 1, ..., N
A
}and {B
i
| i = 1, ..., N
B
} be the set of
position vectors of the feature points in the source
and target images respectively, an energy function E
is defined to guide the movements, as given below:
671
Ni Z. and Leung C..
GENERATION OF FACIAL IMAGE SAMPLES FOR BOOSTING THE PERFORMANCE OF FACE RECOGNITION SYSTEMS.
DOI: 10.5220/0003325506710674
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2011), pages 671-674
ISBN: 978-989-8425-47-8
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

()
()
()
∑∑
∑∑
==
==
−+
⋅−Φ−=
AA
BA
N
j
N
k
Ajk
Ajkjk
N
i
N
j
ijij
ddw
BAfKBAKE
11
2
0
11
1
2
1
,,ln
β
α
(1)
(
)
()
∑
=
−Φ
−Φ
=
A
N
n
nj
kj
jk
KAA
KAA
w
1
2
2
,
,
(2)
where
()
⎟
⎠
⎞
⎜
⎝
⎛
−=Φ
2
2
2
exp,
K
d
Kd
.
Ajk
d
= |A
j
- A
k
| is the current
Euclidean distance between
j
A
and
k
A
while
0
Ajk
d
is
the initial value of
Ajk
d
. K
1
and K
2
are parameters
that define the current size of the neighborhoods of
influence;
(
)
ij
BAf ,
is the correlation coefficient
between the pixel grey levels in a small
neighborhood around
j
A
and that around
i
B
.The
correlation coefficient ranges from -1 to +1 and we
map it to the interval from +0.05 to +1, which means
we give tolerance to those very unlike patterns.
⎩
⎨
⎧
=
x
BAf
ij
05.0
),(
]1,05.0(
]05.0,1[
∈
−∈
x
x
(3)
The energy function E consists of two terms. As
the set of feature points of the source image is
iteratively distorted to match with the target, the first
term measures the distance between the source and
target images while the second measures the amount
of distortion applied to the source image.
α
and
β
are coefficients to weigh the importance of
the two terms. Minimization of E thus tries to match
the two images without excessively distorting the
source image. The parameters K
1
and K
2
serve as a
distance scale factor in the Gaussian function Φ. K
1
and K
2
are set to large values to start with and are
gradually decreased in successive iterations. Please
refer to (Li, et al., 2004) for more discussions on the
coarse-to-fine matching mechanism. Minimization
of E is carried out by gradient descent. Movement
of the feature point
j
j
A
E
A
∂
∂
−=Δ
and is approximately
given by:
()
()
()(){}
∑
∑
=
=
−−−++
−≅Δ
A
B
N
m
jjmmjmmj
N
i
jiijj
AAAAww
ABuA
1
00
1
2
β
α
(4)
()
()
∑
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−−
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−−
=
A
N
n
ni
ni
ji
ji
ij
ABf
K
AB
ABf
K
AB
u
1
2
2
2
2
1
2
,
2
exp
,
2
exp
(5)
Where,
0
j
A is initial value of A
j
.
An example of the matching process is presented
in Fig. 1. Most of the corresponding feature points in
the two images are aligned after the matching.
(a) (b)
Figure 1: (a) Feature points of the source image (red) and
target image (blue). (b) Feature points after 120 iterations.
For each feature point in the source image, the
elastic matching algorithm outputs the displacement
vector that maps it to the corresponding position in
the target image. Using these displacement vectors,
we can generate facial images with expressions in-
between that of the source and target images.
Different from (Beier and Neely, 1992; Karam,
Hassanien, and Nakajima, 2001), we have feature
point correspondence rather than feature line
correspondence for doing warping. We apply an
RBF function to interpolate the remaining (non-
feature point) pixel’s displacements: a pixel’s
displacement is a weighted combination of the
displacements of all feature points, with the largest
weight for the nearest feature point. See equation 6:
() ()
∑
=
−
Δ=Δ
n
i
iii
d
i
yxueayxu
i
1
,,
2
σ
(6)
i
a
is the normalization factor;
),(
iii
yxuΔ
is the
displacement of the i-th feature point,
),( yxuΔ is the
interpolated displacement at position
),( yx . d
i
is the
distance between (x,y) and (x
i
,y
i
). This calculation is
simpler than (Beier and Neely, 1992) and gives a
comparable and good result.
The correspondences need not be strictly a one to
one match. If a feature point cannot find a match
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
672

Figure 2: Some generated faces. The first and last columns are the source and target images respectively, while the rest are
generated images. The top row shows morphing results between different lighting directions; the next two rows show
results between different facial expressions.
in the other image, it is assigned a displacement
according to (6). We use backward mapping to
ensure that every pixel to be interpolated in the
target image can find its corresponding value from
the source image and experimental results are
satisfactory.
We use a “two pass” warping strategy: not only
warp from image A to image B, but also warp from
B to A. Equation 7 depicts the morphing procedure.
It is quite useful where some part is missing in one
image, e.g. one image with teeth and the other
without teeth shown if the mouth is closed. Figure 2
shows some artificial faces generated.
),()1(
),(
BB
AAAB
uimagewarp
uimagewarpimgae
Δ⋅−+
Δ⋅=
α
α
(7)
3 EXPERIMENTS
We first perform the experiment on a standard PCA
with only real samples for training and then repeat
the experiment with the training set augmented by
generated samples (PCA+Vs). In the third
experiment, we add a statistical classifier called
MQDF1 (Kimura, Takashina, Tsuruoka, and
Miyake, 1987) (PCA+Vs+MQDF) on top of the
PCA+Vs method. The same three experiments are
then repeated using an LDA-based platform. We use
the Yale, YaleB and AR databases.
There are 11 images per person in the Yale
database and we choose a subset consisting of
‘normal’, ‘happy’, ‘sad’, ‘right-light’, ‘left-light’,
and ‘surprised’ for training and the rest consisting of
‘center-light’, ‘glasses’, ‘no-glasses’, and ‘wink’ for
testing. A total of 81 training samples per person are
obtained. The recognition rates are shown in Fig. 3.
In Yale-B, we generate intermediate images
between the neutral lighting condition and the other
three lighting conditions. 20 intermediate samples
are generated for each pair and we get 64 training
samples per person. The results are shown in Fig. 4.
The AR database contains images of more than
100 persons; each person has 26 images partitioned
into 2 sessions. We choose the non-occluded images
in the first session for training and the non-occluded
images in the second session for testing.
Intermediate images are generated between the first
image with neutral expression and lighting condition
and the other nine images. For each pair, we
generate 15 intermediate images. The results are
shown in Fig. 5.
Yale
50%
60%
70%
80%
90%
5 15253545
No. eigenvectors
Rec. rate
PCA
PCA+Vs
PCA+Vs+MQDF
Figure 3: PCA based face recognition on the Yale.
YaleB
65%
75%
85%
95%
15 25 35 45
No. eigenvectors
Rec. rate
PCA
PCA+Vs
PCA+Vs+MQDF
Figure 4: PCA based face recognition on the Yale-B.
GENERATION OF FACIAL IMAGE SAMPLES FOR BOOSTING THE PERFORMANCE OF FACE RECOGNITION
SYSTEMS
673
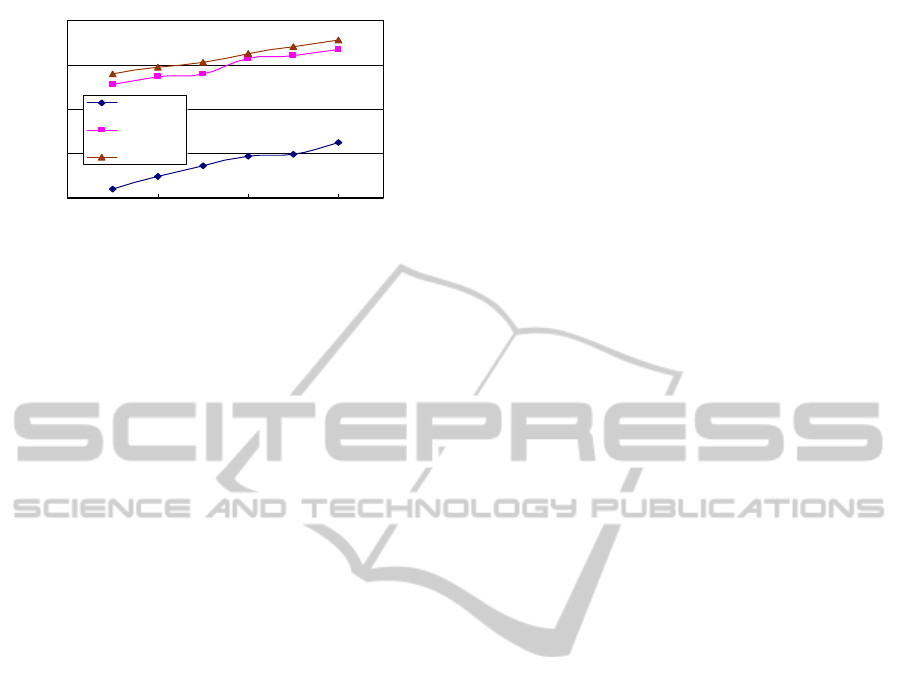
AR
63%
68%
73%
78%
83%
15 25 35 45
No. ei
g
envectors
Rec. rate
PCA
PCA+Vs
PCA+Vs+MQD
Figure 5: PCA based face recognition on the AR.
The above three experiments are repeated on an
LDA based platform instead of PCA. We first
project the grey level face images onto an
eigenspace. All the training and testing sets as well
as generated samples remain unchanged. Similar
improvements in recognition rates are obtained.
4 DISCUSSIONS
AND CONCLUSIONS
We propose an efficient method for matching facial
images and use this method for generating a large
number of additional training samples by matching
and morphing between pairs of real images. The
matching algorithm does not require a one-to-one
correspondence between the set of feature points in
the pair of images. The method is efficient since it
does not involve face modeling and is entirely based
on 2D images. Experiments show that the
recognition rates for PCA and LDA based face
recognition systems are both improved by a large
margin, ranging from 8% to 17%. Moreover, with
the large number of generated samples for training,
more sophisticated statistical classifiers for face
recognition can be used. Experiments show that the
MQDF1 classifier generally gives a higher
recognition rate than the NN-classifier.
A limitation is that it cannot match two images in
which the face orientation is quite different, because
it only relies on 2D information. Also, the
intermediate images generated are not perfect.
Nevertheless the quality is already good enough to
serve as additional training samples.
REFERENCES
Beier, T., & Neely, S. (1992). Feature-Based Image
Metamorphosis. Siggraph 92 : Conference
Proceedings, 26, 35-42.
Cootes, T. F., Edwards, G. J., & Taylor, C. J. (2001).
Active appearance models. Ieee Transactions on
Pattern Analysis and Machine Intelligence, 23(6),
681-685.
Durbin, R., & Willshaw, D. (1987). An Analogue
Approach to the Travelling Salesman Problem Using
an Elastic Net Method. Nature, 326(6114), 689-691.
Karam, H., Hassanien, A., & Nakajima, M. (2001).
Feature-based image metamorphosis optimization
algorithm. Vsmm 2001: Seventh International
Conference on Virtual Systems and Multimedia,
Proceedings, 555-564.
Kimura, F., Takashina, K., Tsuruoka, S., & Miyake, Y.
(1987). Modified Quadratic Discriminant Functions
and the Application to Chinese Character-Recognition.
Ieee Transactions on Pattern Analysis and Machine
Intelligence, 9(1), 149-153.
Lanitis, A., Taylor, C. J., & Cootes, T. F. (1997).
Automatic interpretation and coding of face images
using flexible models. Ieee Transactions on Pattern
Analysis and Machine Intelligence, 19(7), 743-756.
Li, W. C., Leung, C. H., & Hung, Y. S. (2004). Matching
of uncalibrated stereo images by elastic deformation.
International Journal of Imaging Systems and
Technology, 14(5), 198-205.
Martinez, A. M. (2002). Recognizing imprecisely
localized, partially occluded, and expression variant
faces from a single sample per class. Ieee Transactions
on Pattern Analysis and Machine Intelligence, 24(6),
748-763.
Vetter, T., & Poggio, T. (1997). Linear object classes and
image synthesis from a single example image. Ieee
Transactions on Pattern Analysis and Machine
Intelligence, 19(7), 733-742.
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
674
