ACCURATE EYE CENTRE LOCALISATION BY MEANS OF

GRADIENTS

Fabian Timm and Erhardt Barth

Institute for Neuro- and Bioinformatics, University of L

ubeck, Ratzeburger Allee 160, D-23538 L

ubeck, Germany

Pattern Recognition Company GmbH, Innovations Campus L

ubeck, Maria-Goeppert-Strasse 1, D-23562 L

ubeck, Germany

Keywords:

Eye centre localisation, Pupil and iris localisation, Image gradients, Feature extraction, Shape analysis.

Abstract:

The estimation of the eye centres is used in several computer vision applications such as face recognition

or eye tracking. Especially for the latter, systems that are remote and rely on available light have become

very popular and several methods for accurate eye centre localisation have been proposed. Nevertheless, these

methods often fail to accurately estimate the eye centres in difﬁcult scenarios, e.g. low resolution, low contrast,

or occlusions. We therefore propose an approach for accurate and robust eye centre localisation by using

image gradients. We derive a simple objective function, which only consists of dot products. The maximum

of this function corresponds to the location where most gradient vectors intersect and thus to the eye’s centre.

Although simple, our method is invariant to changes in scale, pose, contrast and variations in illumination. We

extensively evaluate our method on the very challenging BioID database for eye centre and iris localisation.

Moreover, we compare our method with a wide range of state of the art methods and demonstrate that our

method yields a signiﬁcant improvement regarding both accuracy and robustness.

1 INTRODUCTION

The localisation of eye centres has signiﬁcant impor-

tance in many computer vision applications such as

human-computer interaction, face recognition, face

matching, user attention or gaze estimation (B

ohme

et al., 2006). There are several techniques for eye

centre localisation, some of them make use of a head-

mounted device, others utilise a chin rest to limit head

movements. Moreover, active infrared illumination is

used to estimate the eye centres accurately through

corneal reﬂections. Although these techniques allow

for very accurate predictions of the eye centres and are

often employed in commercial eye-gaze trackers, they

are uncomfortable and less robust in daylight appli-

cations and outdoor scenarios. Therefore, available-

light methods for eye centre detection have been pro-

posed. These methods can roughly be divided into

three groups: (i) feature-based methods, (ii) model-

based methods, and (iii) hybrid methods. A survey on

video-based eye detection and tracking can be found,

for example, in (Hansen and Ji, 2010).

In this paper we describe a feature-based approach

for eye centre localisation that can efﬁciently and ac-

curately locate and track eye centres in low resolution

images and videos, e.g. in videos taken with a web-

cam. We follow a multi-stage scheme that is usually

performed for feature-based eye centre localisation

(see Figure 1), and we make the following contribu-

tions: (i) a novel approach for eye centre localisation,

which deﬁnes the centre of a (semi-)circular pattern

as the location where most of the image gradients in-

tersect. Therefore, we derive a mathematical function

that reaches its maximum at the centre of the circu-

lar pattern. By using this mathematical formulation

a fast iterative scheme can be derived. (ii) We incor-

porate prior knowledge about the eye appearance and

increase the robustness. (iii) We apply simple post-

processing techniques to reduce problems that arise

in the presence of glasses, reﬂections inside glasses,

or prominent eyebrows. Furthermore, we evaluate the

accuracy and the robustness to changes in lighting,

contrast, and background by using the very challeng-

ing BioID database. The obtained results are exten-

sively compared with state of the art methods for eye

centre localisation.

2 EYE CENTRE LOCALISATION

Geometrically, the centre of a circular object can be

detected by analysing the vector ﬁeld of image gradi-

ents, which has been used for eye centre localisation

125

Timm F. and Barth E..

ACCURATE EYE CENTRE LOCALISATION BY MEANS OF GRADIENTS.

DOI: 10.5220/0003326101250130

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2011), pages 125-130

ISBN: 978-989-8425-47-8

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Multi-stage approach for eye centre localisation.

A face detector is applied ﬁrst; based on the face loca-

tion rough eye regions are extracted (left), which are then

used for a precise estimation of each eye centre (middle and

right).

Figure 2: Artiﬁcial example with a dark circle on a light

background, similar to the iris and the sclera. On the left

the displacement vector d

and the gradient vector g

do not

have the same orientation, whereas on the right both orien-

tations are equal.

previously. Kothari and Mitchell, for example, pro-

posed a method that exploits the ﬂow ﬁeld character

that arises due to the strong contrast between iris and

sclera (Kothari and Mitchell, 1996). They use the ori-

entation of each gradient vector to draw a line through

the whole image and they increase an accumulator bin

each time one such line passes through it. The ac-

cumulator bin where most of the lines intersect thus

represents the estimated eye centre. However, their

approach is only deﬁned in the discrete image space

and a mathematical formulation is missing. More-

over, they don’t consider problems that arise due to

eyebrows, eyelids, or glasses.

In this work, we also analyse the vector ﬁeld of

image gradients but derive a novel mathematical for-

mulation of the vector ﬁeld characteristics. Therefore,

we mathematically describe the relationship between

a possible centre and the orientations of all image gra-

dients. Let c be a possible centre and g

the gradient

vector at position x

. Then, the normalised displace-

ment vector d

should have the same orientation (ex-

cept for the sign) as the gradient g

(see Fig. 2). If we

use the vector ﬁeld of (image) gradients, we can ex-

ploit this vector ﬁeld by computing the dot products

between the normalised displacement vectors (related

to a ﬁxed centre) and the gradient vectors g

. The op-

timal centre c

∗

of a circular object in an image with

pixel positions x

, i ∈ {1,...,N}, is then given by

Figure 3: Evaluation of (1) for an exemplary pupil with the

detected centre marked in white (left). The objective func-

tion achieves a strong maximum at the centre of the pupil;

2-dimensional plot (centre) and 3-dimensional plot (right).

∗

= argmax

(

∑

i=1





)

, (1)

− c

− ck

, ∀i : kg

= 1 . (2)

The displacement vectors d

are scaled to unit length

in order to obtain an equal weight for all pixel posi-

tions. In order to improve robustness to linear changes

in lighting and contrast the gradient vectors should

also be scaled to unit length. An example evalua-

tion of the sum of dot products for different centres is

shown in Fig. 3, where the objective function yields a

strong maximum at the centre of the pupil.

Computational complexity can be decreased by

considering only gradient vectors with a signiﬁ-

cant magnitude, i.e. ignoring gradients in homo-

geneous regions. In order to obtain the image

gradients, we compute the partial derivatives g

(

∂I(x

)

/∂x

∂I(x

)

/∂y

)

, but other methods for com-

puting image gradients will not change the behaviour

of the objective function signiﬁcantly.

2.1 Prior Knowledge and

Postprocessing

Under some conditions, the maximum is not well de-

ﬁned, or there are local maxima that lead to wrong

centre estimates. For example, dominant eyelids and

eyelashes or wrinkles in combination with a low con-

trast between iris and sclera can lead to wrong es-

timates. Therefore, we propose to incorporate prior

knowledge about the eye in order to increase robust-

ness. Since the pupil is usually dark compared to

sclera and skin, we apply a weight w

for each pos-

sible centre c such that dark centres are more likely

than bright centres. Integrating this into the objective

function leads to:

argmax

∑

i=1





, (3)

where w

= I

∗

) is the grey value at (c

) of

the smoothed and inverted input image I

∗

. The image

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

126

needs to be smoothed, e.g. by a Gaussian ﬁlter, in or-

der to avoid problems that arise due to bright outliers

such as reﬂections of glasses. The values of the new

objective function is rather insensitive to changes in

the parameters of the low-pass ﬁlter.

The proposed summation of weighted squared dot

products yields accurate results if the image contains

the eye. However, when applying the multi-stage

scheme described in Figure 1, the rough eye regions

sometimes also contain other structures such as hair,

eyebrows, or glasses. Especially, hair and strong re-

ﬂections in glasses show signiﬁcant image gradients

that do not have the same orientation as the image gra-

dients of the pupil and the iris; hence the estimation

of the eye centres might be wrong. We therefore pro-

pose a postprocessing step in order to overcome these

problems. We apply a threshold on the objective func-

tion, based on the maximum value, and remove all re-

maining values that are connected to one of the image

borders. Then, we determine the maximum of the re-

maining values and use its position as centre estimate.

Based on our experiments the value of this threshold

doesn’t have a signiﬁcant inﬂuence on the centre esti-

mates, we suggest to set this threshold to 90% of the

overall maximum.

3 EVALUATION

For our evaluation we have chosen the BioID

database, since it is the most challenging set of im-

ages for eye centre localisation and many recent re-

sults are available. The database consists of 1521

grey level images of 23 different subjects and has

been taken in different locations and at different day-

times, which result in variable illumination condi-

tions comparable to outdoor scenes. In addition to

the changes in illumination, the position of the sub-

jects change as well as their pose. Moreover, several

subjects wear glasses and some subjects have curled

hair near to the eye centres. In some images the eyes

are closed and the head is turned away from the cam-

era or strongly affected by shadows. In few images

the eyes are even completely hidden by strong reﬂec-

tions on the glasses. Because of these conditions, the

BioID database is considered as one the most chal-

lenging database that reﬂects realistic conditions. The

image quality and the image size (286 × 384) is ap-

proximately equal to the quality of a low-resolution

webcam. The left and right eye centres are annotated

and provided together with the images.

We perform the multi-stage scheme described in

Figure 1, where the position of the face is detected

ﬁrst. Therefore, we apply a boosted cascade face de-

tector that proved to be effective and accurate on sev-

eral benchmarks (Viola and Jones, 2004). Based on

the position of the detected face and anthropometric

relations, we extract rough eye regions relative to the

size of the detected face. The rough eye regions are

then used to estimate the eye centres accurately by

applying the proposed approach.

As accuracy measure for the estimated eye cen-

tres, we evaluate the normalised error, which indi-

cates the error obtained by the worst of both eye esti-

mations. This measure was introduced by Jesorsky et

al. and is deﬁned as:

e ≤

max(e

, e

) , (4)

where e

, e

are the Euclidean distances between the

estimated and the correct left and right eye centres,

and d is the distance between the correct eye centres.

When analysing the performance of an approach for

eye localisation this measure has the following char-

acteristics: (i) e ≤ 0.25 ≈ distance between the eye

centre and the eye corners, (ii) e ≤ 0.10 ≈ diame-

ter of the iris, and (iii) e ≤ 0.05 ≈ diameter of the

pupil. Thus, an approach that should be used for eye

tracking must not only provide a high performance for

e ≤ 0.25, but must yield good results for e ≤ 0.05. An

error of slightly less than or equal to 0.25 will only

indicate that the estimated centre might be located

within the eye, but this estimation cannot be used to

perform accurate eye tracking. When comparing with

state of the art methods we therefore focus on the per-

formance that is obtained for e  0.25.

Since in some other published articles the nor-

malised error is used in a non-standard way, we

also provide the measures e

better

≤

min(e

, e

) and

avg

≤

+ e

) in order to give an upper bound as

well as an averaged error.

3.1 Results

The qualitative results of the proposed approach are

shown in Figure 4. It can be observed that our ap-

proach yields accurate centre estimations not only for

images containing dominant pupils, but also in the

presence of glasses, shadows, low contrast, or strands

of hair. This demonstrates the robustness and proves

that our approach can successfully deal with several

severe problems that arise in realistic scenarios. Our

approach yields inaccurate estimations if the eyes are

(almost) closed or strong reﬂections on the glasses oc-

cur (last row). Then, the gradient orientations of the

pupil and the iris are affected by “noise” and hence

their contribution to the sum of squared dot products

is less than the contribution of the gradients around

the eyebrow or eyelid.

ACCURATE EYE CENTRE LOCALISATION BY MEANS OF GRADIENTS

127

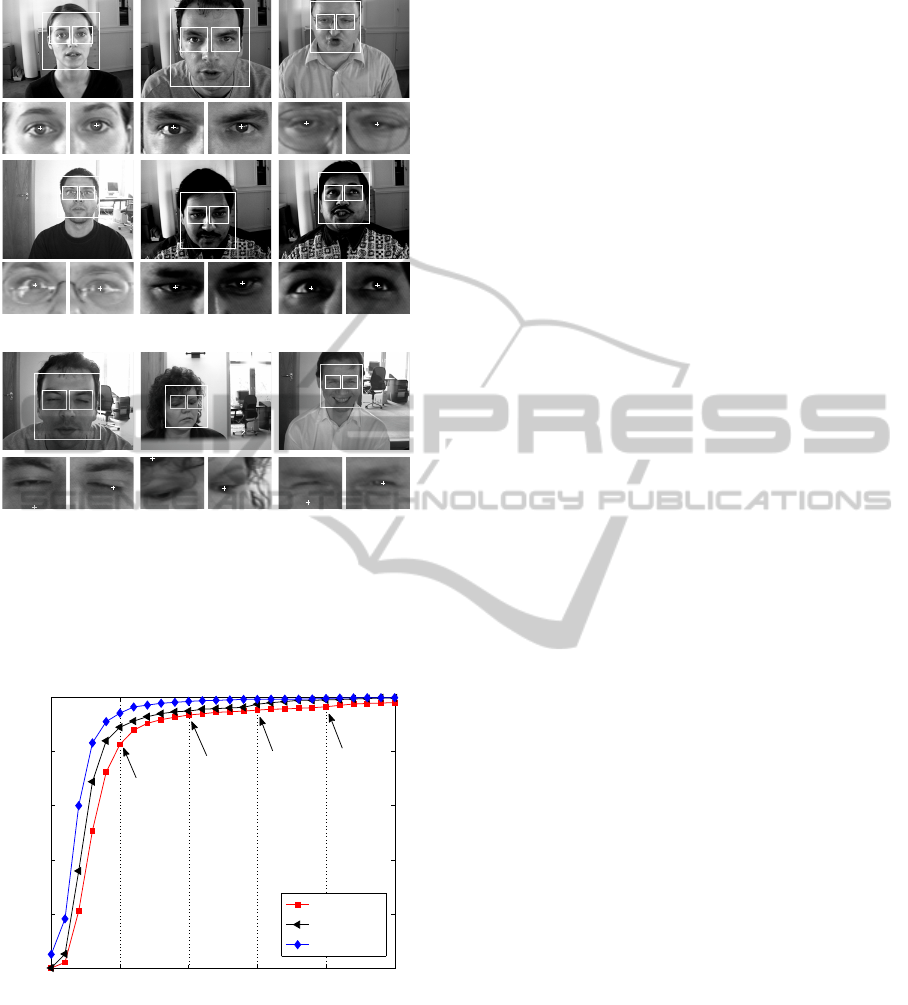
(a) accurate eye centre estimations

(b) inaccurate eye centre estimations

Figure 4: Sample images of accurate and inaccurate results

for eye centre localisation on the BioID database. The esti-

mated centres are depicted by white crosses. Note that, the

estimated centres might be difﬁcult to identify due to low

printer resolution.

0 0.05 0.1 0.15 0.2 0.25

100

normalized error

accuracy [%]

worse eye

avg. eye

better eye

82.5

95.2

93.4

96.4

Figure 5: Quantitative analysis of the proposed approach

for the BioID database. In order to give upper and lower

bounds, the accuracy versus the minimum (better eye,

better

), the maximum (worse eye, e) and the average (avg.

eye, e

avg

) normalised error are shown. Some characteristic

values are given explicitly.

The quantitative results of the proposed method

are shown in Figure 5, where the accuracy measures

e, e

better

, and e

avg

are illustrated. By using the stan-

dard deﬁnition of the normalised error, Eq. (4), our

approach yields an accuracy of 82.5% for pupil lo-

calisation (e ≤ 0.05), which indicates that the cen-

tres detected by our approach are located within the

pupil with high probability and can therefore be used

for eye tracking applications. For iris localisation

(e ≤ 0.10), the estimated centres lie within the iris

with a probability of 93.4%, which will further in-

crease if images with closed eyes are left out.

3.2 Comparison with State of the Art

We extensively compare our method with state of the

art methods that have been applied to the BioID im-

ages as well. For comparison we evaluate the per-

formance for different values of the normalised er-

ror e in order to obtain a characteristic curve (see

Fig. 5 “worse eye”), which we will call worse eye

characteristic (WEC). The WEC is roughly simi-

lar to the well-known receiver operator character-

istic (ROC) and can be analysed in several ways.

As mentioned previously, it depends on the appli-

cation which e should be applied in order to com-

pare different methods, e.g. for eye tracking appli-

cations a high performance for e ≤ 0.05 is required,

whereas for applications that use the overall eye po-

sition such as face matching comparing the perfor-

mance for e ≤ 0.25 will be more appropriate. In or-

der to compare the overall performance, i.e. for dif-

ferent e, the area under the WEC can be used. Un-

fortunately, the WEC of other methods is often not

available, and we therefore compare the methods for

a discretised e ∈ {0.05,0.10,0.15,0.20,0.25}. Fur-

thermore, we also evaluate the rank of each method,

which is roughly inversely proportional to the area un-

der the WEC.

The comparison between our method and state of

the art methods is shown in Tab. 1. If the performance

for e ∈ {0.05, 0.10, 0.15, 0.20, 0.25} was not provided

by the authors explicitly, but a WEC is shown, we

measured the values accurately from the WEC. Note

that, for some methods, the authors evaluated the per-

formance only for few values of e, see for example

(Chen et al., 2006) or (Zhou and Geng, 2004). It can

be seen that our method performs only 2% worse in

average compared to the best method for each e. For

example, the method proposed by Valenti and Gevers

yields a performance of 84.1% for e ≤ 0.05, whereas

our method yields a performance of 82.5%. How-

ever, Valenti and Gevers reported that their method,

which uses mean-shift clustering, SIFT features, and

a k nearest neighbour classiﬁer, will produce unstable

centre estimations when applying it to eye tracking

with several images per second. Hence, our method

can be considered as one of the best methods for

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

128

Table 1: Comparison of the performance for eye detection on the BioID database. Brackets indicate values that have been

accurately measured from author’s graphs. (∗) Images with closed eyes and glasses were omitted. (•) Methods that don’t

involve any kind of learning or model scheme. Since some authors didn’t provide any graphical evaluation of the performance,

e.g. by using a WEC curve, intermediate values couldn’t be estimated – these missing values are denoted by “–”.

Method e ≤ 0.05 e ≤ 0.10 e ≤ 0.15 e ≤ 0.20 e ≤ 0.25 Remarks

(Asadifard and Shanbezadeh, 2010) 47.0% 86.0% 89.0% 93.0% 96.0% (∗), (•)

(Kroon et al., 2008) 65.0% 87.0% – – 98.8%

(Valenti and Gevers, 2008) 77.2% 82.1% (86.2%) (93.8%) 96.4% MIC, (•)

(Valenti and Gevers, 2008) 84.1% 90.9% (93.8%) (97.0%) 98.5% MIC+SIFT+kNN

urkan et al., 2007)

(18.6%) 73.7% (94.2%) (98.7%) 99.6%

(Campadelli et al., 2006) 62.0% 85.2% 87.6% 91.6% 96.1%

(Niu et al., 2006) (75.0%) 93.0% (95.8%) (96.4%) (97.0%)

(Chen et al., 2006) – 89.7% – – 95.7%

(Asteriadis et al., 2006) (44.0%) 81.7% (92.6%) (96.0%) 97.4% (•)

(Hamouz et al., 2005) (58.6%) (75.0%) (80.8%) (87.6%) (91.0%)

(Zhou and Geng, 2004) – – – – 94.8% (•)

(Cristinacce et al., 2004) (57.0%) 96.0% (96.5%) (97.0%) (97.1%)

(Behnke, 2002) (37.0%) (86.0%) (95.0%) (97.5%) (98.0%)

(Jesorsky et al., 2001) (38.0%) (78.8%) (84.7%) (87.2%) 91.8%

our method 82.5% 93.4% 95.2% 96.4% 98.0% (•)

accurate eye centre localisation. Furthermore, our

method has signiﬁcantly less computational complex-

ity compared to that of Valenti and Gevers, since it

requires neither clustering nor a classiﬁer. Compar-

ing those methods that do not involve any kind of

learning scheme, our method achieves the best per-

formance by far (82.5% for e ≤ 0.05). For iris loca-

tion (e ≤ 0.10), our method achieves the second best

performance (93.4%); only the method by Cristinacce

et al. yields a signiﬁcant improvement (96.0%) –

however, this improvement implies, again, a higher

computational complexity compared to our method,

which is solely based on dot products. For higher nor-

malised errors, e.g. e ≤ 0.15, e ≤ 0.20, or e ≤ 0.25,

our method performs comparable to other methods.

A comparison based on the ranks of the perfor-

mances is shown in Tab. 2. It can be seen clearly,

that there isn’t one single method that performs supe-

rior for all values of e. Exemplarily, the method pro-

posed by T

urkan et al. achieves accurate estimations

for detecting the overall eye centres, i.e. e ≤ 0.20 and

e ≤ 0.25, but it fails for iris localisation (e ≤ 0.10)

and pupil localisation (e ≤ 0.05) with rank 13 in both

cases. In contrast, our method ranks 2nd for both

pupil and iris localisation and ranks 3rd and 4th for

larger e. Hence, our method doesn’t yield the best re-

sult for one single e, but if we evaluate the average

rank our method yields the best result (3.0). Com-

pared to the method with the second best average

rank (3.4, Valenti and Gevers, MIC+SIFT+kNN) our

method is not only superior according to the average

rank, but also the variance of the individual ranks is

signiﬁcantly less, and the complexity is much lower.

In total, our method performs comparable to other

state of the art methods when looking for a particular

e, but it yields the best average performance over all

values of e. Hence, our method proves to be powerful

for several problems such as eye centre localisation

(e ≤ 0.05), iris localisation (e ≤ 0.10), and eye lo-

calisation (e ≤ 0.25). Comparing only those methods

that do not apply any learning scheme, our method

achieves signiﬁcant improvements for the more difﬁ-

cult tasks, i.e. 5% improvement for e ≤ 0.05, 7% for

e ≤ 0.10, and 2.6% for e ≤ 0.15.

4 CONCLUSIONS

We propose a novel algorithm for accurate eye cen-

tre localisation based on image gradients. For ev-

ery pixel, we compute the squared dot product be-

tween the displacement vector of a centre candidate

and the image gradient. The position of the maxi-

mum then corresponds to the position where most im-

age gradients intersect. Our method yields low com-

putational complexity and is invariant to rotation and

linear changes in illumination. Compared to several

state of the art methods, our method yields a very high

accuracy for special scenarios such as pupil localisa-

tion (2nd place) and ranks in 1st place if the average

performance over several scenarios, e.g. pupil local-

isation, iris localisation, and overall eye localisation,

is evaluated. Our method can be applied to several

(real-time) applications that require a high accuracy

such as eye tracking or medical imaging analysis (cell

tracking).

ACCURATE EYE CENTRE LOCALISATION BY MEANS OF GRADIENTS

129

Table 2: Comparison of ranks of each method according to its performance shown in Tab. 1.

Method e ≤ 0.05 e ≤ 0.10 e ≤ 0.15 e ≤ 0.20 e ≤ 0.25 avg. rank

(Asadifard and Shanbezadeh, 2010) 9 7 8 7 10 8.2

(Kroon et al., 2008) 5 6 – – 2 4.3

(Valenti and Gevers, 2008) 3 9 10 6 8 7.2

(Valenti and Gevers, 2008) 1 4 6 3 3 3.4

urkan et al., 2007) 13 13 5 1 1 6.6

(Campadelli et al., 2006) 6 8 9 8 9 8.0

(Niu et al., 2006) 4 3 2 4 7 4.0

(Chen et al., 2006) – 5 – – 11 8.0

(Asteriadis et al., 2006) 10 10 7 5 5 7.4

(Hamouz et al., 2005) 7 12 12 9 14 10.8

(Zhou and Geng, 2004) – – – – 12 12.0

(Cristinacce et al., 2004) 8 1 1 3 6 3.8

(Behnke, 2002) 12 7 4 2 4 5.8

(Jesorsky et al., 2001) 11 11 11 10 13 11.2

our method 2 2 3 4 4 3.0

REFERENCES

Asadifard, M. and Shanbezadeh, J. (2010). Automatic adap-

tive center of pupil detection using face detection and

cdf analysis. In Proceedings of the IMECS, volume I,

pages 130–133, Hong Kong. Newswood Limited.

Asteriadis, S., Asteriadis, S., Nikolaidis, N., Hajdu, A., and

Pitas, I. (2006). An eye detection algorithm using

pixel to edge information. In Proceedings of the 2nd

ISCCSP, Marrakech, Morocco. EURASIP.

Behnke, S. (2002). Learning face localization using hi-

erarchical recurrent networks. In Proceedings of the

ICANN, LNCS, pages 135–135. Springer.

ohme, M., Meyer, A., Martinetz, T., and Barth, E. (2006).

Remote eye tracking: State of the art and directions

for future development. In Proceedings of the 2nd

COGAIN, pages 10–15, Turin, Italy.

Campadelli, P., Lanzarotti, R., and Lipori, G. (2006).

Precise eye localization through a general-to-speciﬁc

model deﬁnition. In Proceedings of the 17th BMVC,

volume I, pages 187–196, Edingburgh, England.

Chen, D., Tang, X., Ou, Z., and Xi, N. (2006). A hierar-

chical ﬂoatboost and mlp classiﬁer for mobile phone

embedded eye location system. In Proceedings of the

3rd ISNN, LNCS, pages 20–25, China. Springer.

Cristinacce, D., Cootes, T., and Scott, I. (2004). A multi-

stage approach to facial feature detection. In Proceed-

ings of the 15th BMVC, pages 277–286, England.

Hamouz, M., Kittler, J., Kamarainen, J., Paalanen, P.,

alvi

ainen, H., and Matas, J. (2005). Feature-based

afﬁne-invariant localization of faces. IEEE Transac-

tions on PAMI, 27(9):1490.

Hansen, D. and Ji, Q. (2010). In the eye of the beholder: A

survey of models for eyes and gaze. IEEE Trans. on

PAMI, 32(3):478–500.

Jesorsky, O., Kirchberg, K., and Frischholz, R. (2001). Ro-

bust face detection using the Hausdorff distance. In

Proceedings of the 3rd AVBPA, LNCS, pages 90–95,

Halmstad, Sweden. Springer.

Kothari, R. and Mitchell, J. (1996). Detection of eye loca-

tions in unconstrained visual images. In Proceedings

of the IEEE ICIP, volume 3, pages 519–522. IEEE.

Kroon, B., Hanjalic, A., and Maas, S. (2008). Eye localiza-

tion for face matching: is it always useful and under

what conditions? In Proceedings of the 2008 CIVR,

pages 379–388, Ontario, Canada. ACM.

Niu, Z., Shan, S., Yan, S., Chen, X., and Gao, W. (2006).

2d cascaded adaboost for eye localization. In Proceed-

ings of the 18th IEEE ICPR, volume 2, pages 1216–

1219, Hong Kong. IEEE.

urkan, M., Pard

as, M., and C¸ etin, A. E. (2007). Human

eye localization using edge projections. In Proceed-

ings of the 2nd VISAPP, pages 410–415. INSTICC.

Valenti, R. and Gevers, T. (2008). Accurate eye center lo-

cation and tracking using isophote curvature. In Pro-

ceedings of the CVPR, pages 1–8, Alaska. IEEE.

Viola, P. and Jones, M. (2004). Robust real-time face detec-

tion. IJCV, 57(2):137–154.

Zhou, Z. and Geng, X. (2004). Projection functions for eye

detection. Pattern Recognition, 37(5):1049–1056.

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

130